КРИВІ ДРУГОГО ПОРЯДКУ • Криві другого

КРИВІ ДРУГОГО ПОРЯДКУ

• Криві другого порядку – це всі точки площини, координати яких задовольняють рівнянню F ( x , y ) = 0, де F ( x , y ) – многочлен другої степені. 0 22 FEy. Dx. Cy. Bxy. Ax

Криві другого порядку діляться на 1) вироджені 2) невироджені точки еліпс порожня множина коло прямі гіпербола параллельных парабола. або перетинающихся прямих Якщо рівнянню другого порядку не задовольняє жодна точка площини, то говорять, що рівняння визначає вироджену неявну криву (неявну криву другого порядку).

1. Еліпс і коло ОЗНАЧЕННЯ. Еліпсом називається геометричне місце точок площини, сума відстаней від яких до двох фіксованих точок площини F 1 і F 2 величина стала і дорівнює 2 a (2 a >| F 1 F 2 |). Точки F 1 і F 2 називають фокусами еліпса. Виберемо декартову прямокутну систему координат так, щоб фокуси F 1 і F 2 лежали на осі Ox на однаковій відстані від O. В такій системі координат F 1 (– c ; 0) і F 2 ( c ; 0) , де | OF 1 | = | OF 2 | = c. O 1 F 2 F M

Рівняння (1)12 2 b y a x називається канонічним рівнянням еліпса. Система координат, в якій еліпс має таке рівняння називається його канонічною системою координат.

ДОСЛІДЖЕННЯ КАНОНІЧНОГО РІВНЯННЯ Е ЛІПСА 1) Еліпс лежить всередині прямокутника, обмеженого x = a , y = b. 2) Еліпс має центр симетрії (початок координат) і дві осі симетрії (осі Ox і Oy ). Центр симетрії еліпса називають центром еліпса. Вісь симетрії еліпса, що проходить через фокуси (вісь Ox ) називають великою (або фокальною) віссю симетрії , а другу вісь (вісь Oy ) – малою віссю. 3) З рівняння еліпса отримаємо Проведемо дослідження кривої 22 xa ab y 22 xa a b y

а ) D ( y ) = [– a ; a ] , y ( a ) = 0 ; б) функція зростає при x (– a ; 0) ( y > 0) , спадає при x (0; a ) ( y < 0) , е кстремум (максимум) в точці x = 0 , y (0) = b ; в) крива завжди опукла . 22 xa x a b y 0 )( 322 xa ab y

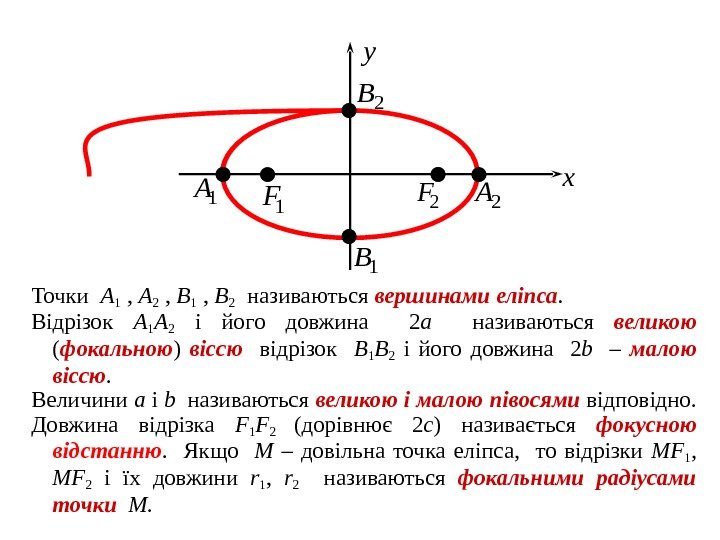
Точки A 1 , A 2 , B 1 , B 2 називаються вершинами еліпса. Відрізок A 1 A 2 і його довжина 2 a називаються великою ( фокальною ) віссю відрізок B 1 B 2 і його довжина 2 b – малою віссю. Величини a і b називаються великою і малою півосями відповідно. Довжина відрізка F 1 F 2 (дорівнює 2 c ) називається фокусною відстанню. Якщо M – довільна точка еліпса, то відрізки MF 1 , MF 2 і їх довжини r 1 , r 2 називаються фокальними радіусами точки M. 1 A 1 F 2 A 1 B 2 B 2 F x y

ОЗНАЧЕННЯ. Величина , що дорівнює відношенню фокусної відстані еліпса до його більшої осі , називається ексцентриситетом еліпса, тобто . 2 2 a c Оскільки , то 0 < < 1 . Величина характеризує форму еліпса. Якщо відомий еліпса легко знайти фокальні радіуси точки M ( x ; y ): r 1 = | MF 1 | = a + x , r 2 = | MF 2 | = a – x . Зауваження. 1) Нехай в рівнянні еліпса a = b = r. Для цієї кривої F 1 = F 2 = O , Геометрично це означає, що точки кривої рівновіддалені (на відстані r ) від її центра O , тобто крива є колом. Канонічне рівняння кола прийнято записувати у виді x 2 + y 2 = r 2 , де r – відстань від довільної точки кола до її центра; r називають радіусом кола. abac 22 0 22 bac. 0 a c

2) Якщо вибрати систему координат так, щоб фокуси F 1 і F 2 були на осі Oy на однаковій відстані від початку координат, то рівняння еліпса буде мати вид. 12 2 a y b x Для цього еліпса велика вісь – вісь Oy , мала вісь – вісь Ox , фокуси мають координати F 1 (0; – c ) і F 2 (0; c ) , де. 22 bac Ф окальні радіуси точки M ( x ; y ) знаходять за формулами r 1 = | MF 1 | = a + y , r 2 = | MF 2 | = a – y . 1 A 1 F 2 A 1 B 2 B 2 F x y

2. Гіпербола ОЗЕАЧЕННЯ. Гіперболою називається геометричне місце точок площини, модуль різниці відстаней від яких до двох фіксованих точок площини F 1 і F 2 величина стала і дорівнює 2 a (2 a < | F 1 F 2 |). Точки F 1 і F 2 називають фокусами гіперболи. Виберемо декартову прямокутну систему координат так, щоб фокуси F 1 і F 2 лежали на осі Ox на однаковій відстані від O. В такій системі координат F 1 (– c ; 0) і F 2 ( c ; 0) , де | OF 1 | = | OF 2 | = c. O 1 F 2 F M

Рівняння (2) 1 2 2 b y a x називається канонічним рівнянням гіперболи. Система координат, в якій гіпербола має таке рівняння, називається її канонічною системою координат.

ДОСЛІДЖЕННЯ КАНОНІЧНОГО РІВНЯННЯ ГІПЕРБОЛИ 1) точок гіперболи немає в полосі, обмеженій прямими x = a. 2) г іпербола має центр симетрії (початок координат) і дві осі симетрії (осі Ox і Oy ). Центр симетрії гіперболи називають центром гіперболи. Вісь симетрії гіперболи, що проходить через фокуси (вісь Ox ) називають дійсною (або фокальною ) віссю симетрії, а іншу вісь (вісь Oy ) – уявною віссю. 3) з рівняння гіперболи отримаємо Проведемо дослідження кривої. 22 ax a b y

а) D ( y ) = (– ; – a ] ∪ [ a ; + ) , y ( a ) = 0 ; б) лінія має асимптоти Нагадаємо що пряма ℓ називається асимптотою кривої, якщо відстань від точки M кривої до прямої ℓ наближається до нуля при віддаленні точки M від початку координат. Існують два види асимптот: вертикальні і похилі. Вертикальні асимптоти крива y = f ( x ) має в тих точках розриву II роду функції y = f ( x ), в яких принаймні одна з односторонніх границь функції дорівнює нескінченності. Похилі асимптоти кривої y = f ( x ) мають рівняння y = k 1, 2 x + b 1, 2 , де x xf k x )( lim 2, 1 , xkxfb x 2, 1 )(lim . 22 ax a b y

в) функція зростає при x ( a ; + ) ( y > 0) , спадає при x ( – ; – a ) ( y < 0) , е кстремумі в не має ( критичні точки x = 0 D ( y ) і x = a – граничні) ; г) крива завжди опукла. 22 ax x a b y 0 )( 322 ax ab y

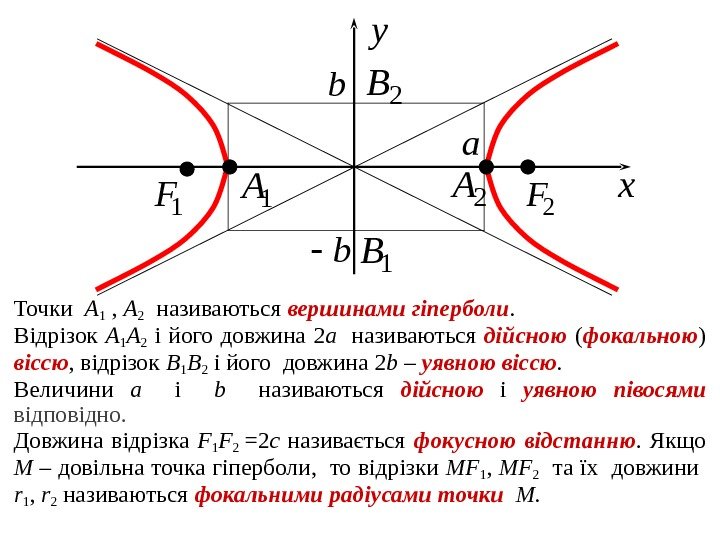
Точки A 1 , A 2 називаються вершинами гіперболи. Відрізок A 1 A 2 і його довжина 2 a називаються дійсною ( фокальною ) віссю , відрізок B 1 B 2 і його довжина 2 b – уявною віссю. Величини a і b називаються дійсною і уявною півосями відповідно. Довжина відрізка F 1 F 2 =2 c називається фокусною відстанню. Якщо M – довільна точка гіперболи , то відрізки MF 1 , MF 2 та їх довжини r 1 , r 2 називаються фокальними радіусами точки M. 1 A 1 F 2 A b 2 Fx y a b

ОЗНАЧЕННЯ. Величина , дорівнює відношенню фокусної відстані від гіперболи до її дійсної осі , називається ексцентриситетом гіперболи , тобто . 2 2 a c Оскільки , то > 1 . Величина характеризує форму гіперболи. Якщо відомий ексцентриситет гіперболи легко знайти фокальні радіуси точки M ( x ; y ). Якщо точка M лежить на правій гільці гіперболи (тобто x > 0 ), то r 1 = | MF 1 | = a + x , r 2 = | MF 2 | = – a + x . Якщо M лежить на лівій гільці гіперболи (тобто x < 0 ), то r 1 = | MF 1 | = – ( a + x ), r 2 = | MF 2 | = – (– a + x ). abac

Зауваження. 1) Якщо в рівнянні гіперболи a = b , то гіпербола називається рівнобічною. Асимптоти рівнобічної гіперболи, перпендикулярні. Тоді можна вибрати систему координат так, щоб координатні осі співпали з асимптотами. Тоді рівняння гіперболи буде xy =0, 5 a 2 . (3) Рівняння (3) називають рівнянням рівнобічної гіперболи , відносно асимптот.

2) Якщо вибрати систему координат так, щоб фокуси F 1 і F 2 були на однаковій відстані від O (0; 0), але лежали на Oy , то рівняння гіперболи буде мати вид. 12 2 a y b x 1 A 1 F 2 A b 2 F x y a b Для цієї гіперболи дійсна вісь – вісь Oy , уявна вісь – вісь Ox , F 1 (0; – c ) і F 2 (0; c ) (де ) 22 bac Асимптоти: , x b a y фокальні радіуси точки M ( x ; y ) знаходять з а формулами: а) при y > 0 r 1 =| MF 1 | = a + y , r 2 =| MF 2 | = – a + y ; б) при y < 0 r 1 =| MF 1 |= –( a + x ), r 2 =| MF 2 |= –(– a + x ).

3. Парабола Нехай ℓ – довільна пряма на площині , F – довільна точка площини, що не лежить на прямій ℓ. ОЗНАЧЕННЯ. Параболою називається геометричне місце точок площини, відстань від яких до фіксованої прямої ℓ і до фіксованої точки F (що не лежить на прямій ℓ) однакова. Точку F називають фокусом параболи, пряму ℓ — директрисою. Виберемо декартову прямокутну систему координат так, щоб директриса параболи ℓ була перпендикулярною осі Ox, фокус F лежав на додатній частині Ox і відстань від O до F і до ℓ була однакова В такій системі координат F ( 0, 5 p ; 0) і ℓ : x + 0, 5 p =0 , де p – відстань від F до ℓ . OF M

Рівняння (4) y 2 = 2 px називається канонічним рівнянням параболи. Система координат, в якій парабола має таке рівняння , називається її канонічною системою координат.

ДОСЛІДЖЕННЯ КАНОНІЧНОГО РІВНЯННЯ ПАРАБОЛИ 1) парабола лежить у півплощині x ≥ 0. 2) п арабола має вісь симетрії (вісь Ox ). Ві сь симетрії параболи називають віссю параболи. 3) з рівняння параболи отримаємо : Проведемо дослідження кривої : а) D ( y ) = [0; + ) , y (0) = 0 ; б) асимптот не має; в) функція завжди зростає ; г) крива завжди опукла. . 2 pxy 2 0 2 2 x p y 0 4 2 3 x p y

Точка, в якій парабола перетинає свою вісь, називається вершиною параболи. Ч исло p називається параметром параболи. Якщо M – довільна точка параболи, то відрізок MF і його довжина називаються фокальними радіусами точки M. p Fx y

Зауваження. Введемо систему координат так, щоб фокус F параболи лежав на від’ємній частині осі Ox , директриса була перпендикулярна Ox , і відстань від O до F і до директриси була однакова. y x. F p Тоді отримаємо для параболи рівняння y 2 = – 2 px , (5) а для директриси і фокуса F (– 0, 5 p ; 0) и ℓ : x – 0, 5 p = 0.

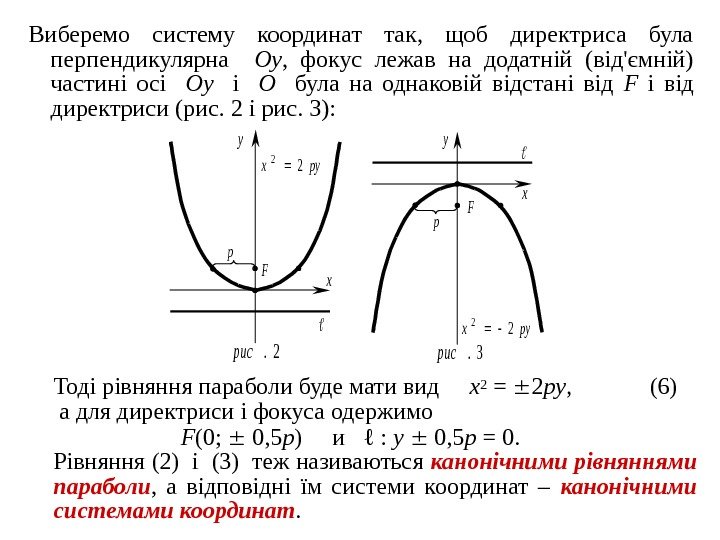
Виберемо систему координат так, щоб директриса була перпендикулярна Oy , фокус лежав на додатній (від’ємній) частині осі Oy і O була на однаковій відстані від F і від директриси (рис. 2 і рис. 3) : Тоді рівняння параболи буде мати вид x 2 = 2 py , (6) а для директриси і фокуса одержимо F (0; 0, 5 p ) и ℓ : y 0, 5 p = 0. Рівняння (2) і (3) теж називаються канонічними рівняннями параболи , а відповідні їм системи координат – канонічними системами координат. p F x y y x F p 2. рис3. рис pyx