Колебания Колебания—этоповторяющийсявтойилииной степенивовременипроцессизменениясостоянийсистемы околоточкиравновесия. Например, при колебанияхмаятникаповторяютсяотклоненияеговтуи

Колебания—этоповторяющийсявтойилииной степенивовременипроцессизменениясостоянийсистемы околоточкиравновесия. Например, при колебанияхмаятникаповторяютсяотклоненияеговтуи другуюсторонуотвертикальногоположения; при колебанияхвэлектрическомколебательном контуреповторяютсявеличинаинаправлениетока, текущего черезкатушку.

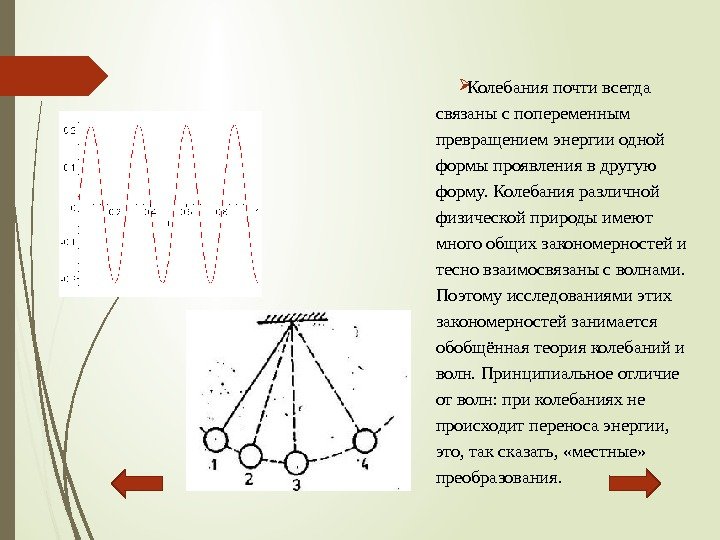
Колебанияпочтивсегда связаныспопеременным превращениемэнергииодной формыпроявлениявдругую форму. Колебанияразличной физическойприродыимеют многообщихзакономерностейи тесновзаимосвязаныcволнами. Поэтомуисследованиямиэтих закономерностейзанимается обобщённаятеорияколебанийи волн. Принципиальноеотличие отволн: приколебанияхне происходитпереносаэнергии, это, таксказать, «местные» преобразования.

Виды колебаний Свободные Вынужденные Гармонические Резонанс Автоколебания Параметрические

Свободные колебания (или собственные колебания )—этоколебания колебательнойсистемы, совершаемыетолькоблагодаряпервоначальносообщенной энергии( потенциальной или кинетической )приотсутствиивнешнихвоздействий. Потенциальнаяиликинетическаяэнергияможетбытьсообщена, например, в механическихсистемахчерезначальноесмещениеилиначальнуюскорость. Свободноколеблющиесятелавсегдавзаимодействуютсдругимителамиивместес нимиобразуютсистемутел, котораяназывается колебательной системой. Силы, действующиемеждутеламиколебательнойсистемы, называются внутренними силами. Внешними силами называютсясилы, действующие насистемусосторонытел, невходящихвнее. Сэтойточкизрениясвободныеколебания можноопределитькакколебаниявсистемеподдействиемвнутреннихсилпослетого, как системавыведенаизположенияравновесия. Условиямивозникновениясвободныхколебанийявляются: 1)возникновениевнихсилы, возвращающейсистемувположениеустойчивого равновесия, послетогокакеевывелиизэтогосостояния; 2)отсутствиетрениявсистеме.

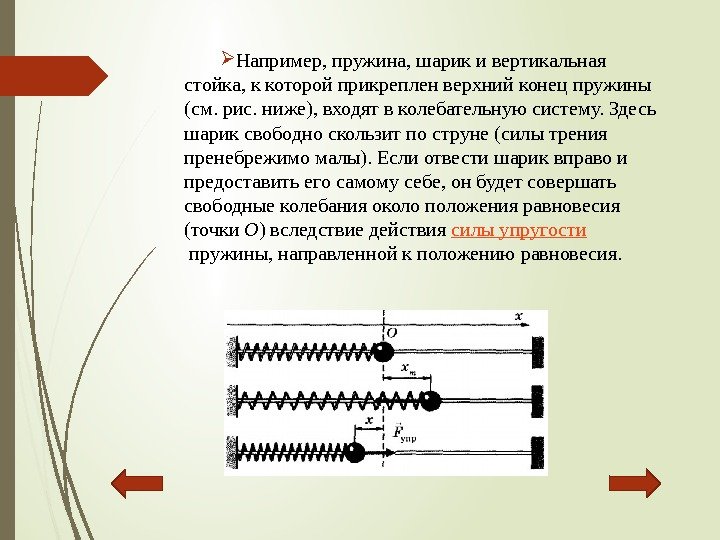
Например, пружина, шарикивертикальная стойка, ккоторойприкрепленверхнийконецпружины (см. рис. ниже), входятвколебательнуюсистему. Здесь шариксвободноскользитпоструне(силытрения пренебрежимомалы). Еслиотвестишариквправои предоставитьегосамомусебе, онбудетсовершать свободныеколебанияоколоположенияравновесия (точки О )вследствиедействия силыупругости пружины, направленнойкположениюравновесия.

Другимклассическимпримероммеханической колебательнойсистемыявляетсяматематический маятник(см. рис. ниже). Вданномслучаешарик совершаетсвободныеколебанияподдействиемдвух сил: силытяжести исилыупругостинити(в колебательнуюсистемувходиттакже. Земля). Их равнодействующаянаправленакположению равновесия.

Вынужденные колебания Вынужденными называютсятакиеколебания, которыевозникаютвколебательнойсистемепод действиемвнешнейпериодическиизменяющейсясилы. Этасила, какправило, выполняетдвоякуюроль: онараскачиваетсистемуисообщаетей определенныйзапасэнергии, атакжеонапериодическивосполняетпотериэнергии(расходэнергии) напреодолениесилсопротивленияитрения. Периодическаявнешняясиламожетизменятьсявовременипоразличнымзаконам. Особый интереспредставляетслучай, когдавнешняясила, изменяющаясяпогармоническомузаконус частотойω, воздействуетнаколебательнуюсистему, способнуюсовершатьсобственныеколебанияна некоторойчастотеω 0. Еслисвободныеколебанияпроисходятначастотеω 0 , котораяопределяетсяпараметрамисистемы, то установившиеся вынужденные колебания всегда происходят на частотеωвнешнейсилы.

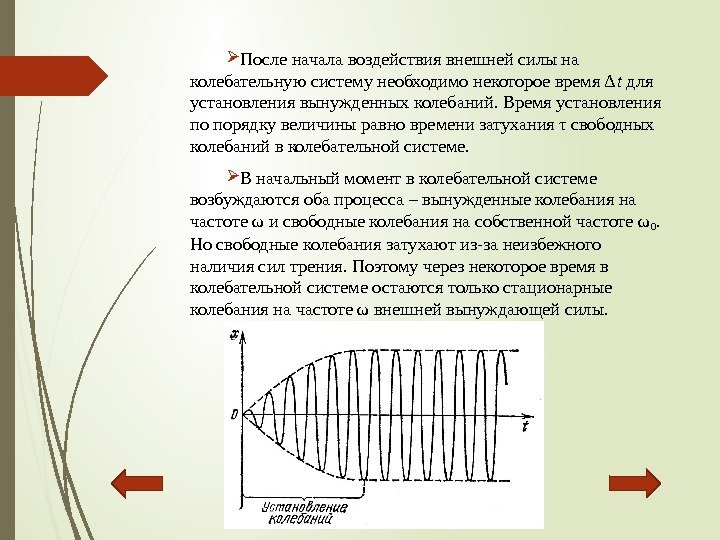
Посленачалавоздействиявнешнейсилына колебательнуюсистемунеобходимонекотороевремяΔ t для установлениявынужденныхколебаний. Времяустановления попорядкувеличиныравновременизатуханияτсвободных колебанийвколебательнойсистеме. Вначальныймоментвколебательнойсистеме возбуждаютсяобапроцесса–вынужденныеколебанияна частотеωисвободныеколебаниянасобственнойчастотеω0. Носвободныеколебаниязатухаютиз-занеизбежного наличиясилтрения. Поэтомучерезнекотороевремяв колебательнойсистемеостаютсятолькостационарные колебанияначастотеωвнешнейвынуждающейсилы.

Есличастотаωвнешнейсилыприближаетсяксобственнойчастотеω 0 , возникаетрезкоевозрастаниеамплитудывынужденныхколебаний. Этоявление называется резонансом. Зависимостьамплитуды x m вынужденныхколебанийот частотыωвынуждающейсилыназывается резонансной характеристикой или резонансной кривой. Прирезонансе амплитуда x m колебаниягрузаможетвомногоразпревосходить амплитуду y m колебанийсвободного(левого)концапружины, вызванного внешнимвоздействием. Вотсутствиетренияамплитудавынужденных колебанийприрезонанседолжнанеограниченновозрастать. Вреальных условияхамплитудаустановившихсявынужденныхколебанийопределяется условием: работавнешнейсилывтечениепериодаколебанийдолжнаравняться потеряммеханическойэнергиизатожевремяиз-затрения. Чемменьшетрение (т. е. чемвышедобротность Q колебательнойсистемы), тембольшеамплитуда вынужденныхколебанийприрезонансе.

Гармонические колебания —это колебания , прикоторых физическаявеличина меняетсявовременипосинусоидальномузакону: где х —значениеколеблющейсявеличинывмоментвремени t , А —амплитуда , ω —круговаячастота, φ —начальнаяфазаколебаний, ( φt+ φ ) —полная фазаколебаний. Приэтомвеличины А , ω и φ —постоянные. Длямеханическихколебанийколеблющейсявеличиной х являются, в частности, смещениеи скорость , дляэлектрическихколебаний—напряжение и силатока. Гармоническиеколебаниязанимаютособоеместосредивсехвидов колебаний, т. к. этоединственныйтипколебаний, формакоторыхне искажаетсяприпрохождениичерезлюбуюоднороднуюсреду, т. е. волны, распространяющиесяотисточникагармоническихколебаний, такжебудут гармоническими. Любоенегармоническоеколебаниеможетбытьпредставлено ввидесумм( интеграла )различныхгармоническихколебаний(ввидеспектра гармоническихколебаний).

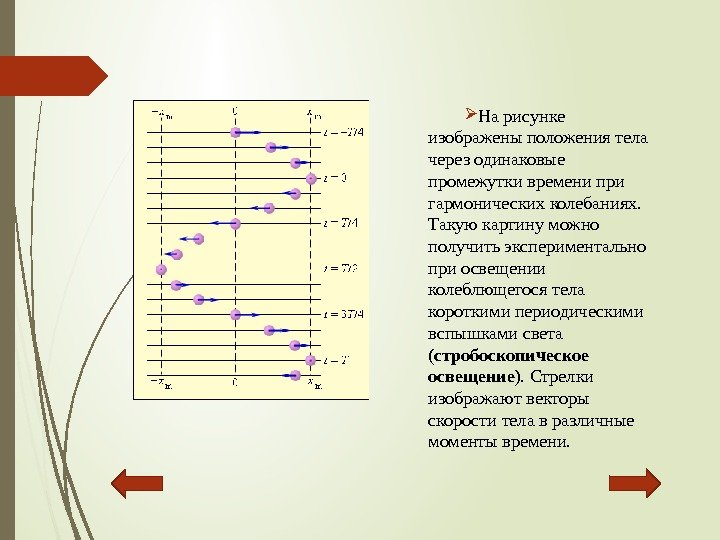
Нарисунке изображеныположениятела черезодинаковые промежуткивременипри гармоническихколебаниях. Такуюкартинуможно получитьэкспериментально приосвещении колеблющегосятела короткимипериодическими вспышкамисвета ( стробоскопическое освещение ). Стрелки изображаютвекторы скоростителавразличные моментывремени.

Резонанс —явление, прикотором амплитуда вынужденных колебаний имеетмаксимумпринекоторомзначении частоты вынуждающейсилы. Частоэтозначениеблизкок частоте собственных колебаний, фактическиможетсовпадать, ноэтоневсегдатакине являетсяпричинойрезонанса. Врезультатерезонансапринекоторойчастотевынуждающей силыколебательнаясистемаоказываетсяособенноотзывчивойна действиеэтойсилы. Степеньотзывчивостивтеорииколебаний описываетсявеличиной, называемой добротностью. Припомощи резонансаможновыделитьи/илиусилитьдажевесьмаслабые периодическиеколебания. Явлениерезонансавпервыебылоописано Галилео. Галилеем в 1602 г. вработах, посвященныхисследованию маятников и музыкальныхструн.

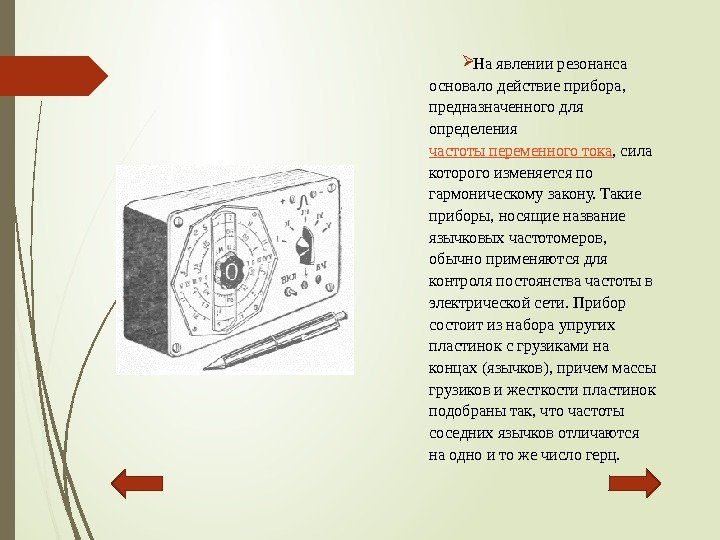
Наявлениирезонанса основалодействиеприбора, предназначенногодля определения частотыпеременноготока , сила которогоизменяетсяпо гармоническомузакону. Такие приборы, носящиеназвание язычковыхчастотомеров, обычноприменяютсядля контроляпостоянствачастотыв электрическойсети. Прибор состоитизнабораупругих пластиноксгрузикамина концах(язычков), причеммассы грузиковижесткостипластинок подобранытак, чточастоты соседнихязычковотличаются наодноитожечислогерц.

Автоколебания—незатухающиеколебания вдиссипативнойдинамическойсистемес нелинейнойобратнойсвязью, поддерживающиеся засчётэнергиипостоянного, то естьнепериодическоговнешнеговоздействия. Автоколебанияотличаютсяотвынужденных колебанийтем, чтопоследние вызваныпериодическимвнешнимвоздействиеми происходятсчастотойэтоговоздействия, втовремя каквозникновениеавтоколебанийи ихчастотаопределяютсявнутреннимисвойствами самойавтоколебательнойсистемы. Терминавтоколебанияврусскоязычную терминологиювведён. А. А. Андроновымв 1928 году. Примерамиавтоколебаниймогутслужить: незатухающиеколебаниямаятникачасовза счётпостоянногодействиятяжестизаводнойгири, колебанияскрипичнойструныподвоздействием равномернодвижущегосясмычка.

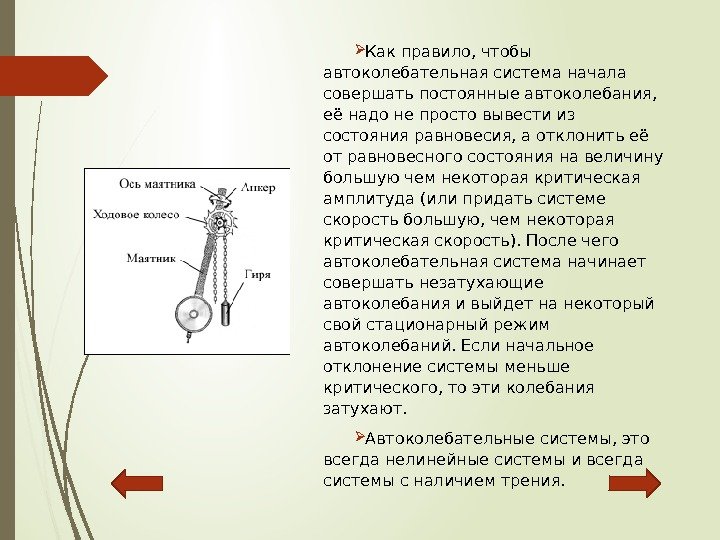
Как правило, чтобы автоколебательная система начала совершать постоянные автоколебания, её надо не просто вывести из состояния равновесия, а отклонить её от равновесного состояния на величину большую чем некоторая критическая амплитуда (или придать системе скорость большую, чем некоторая критическая скорость). После чего автоколебательная система начинает совершать незатухающие автоколебания и выйдет на некоторый свой стационарный режим автоколебаний. Если начальное отклонение системы меньше критического, то эти колебания затухают. Автоколебательные системы, это всегда нелинейные системы и всегда системы с наличием трения.

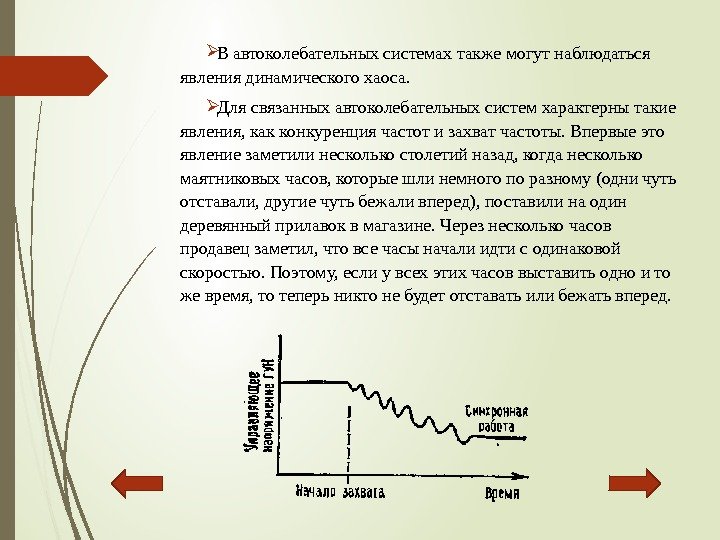
Вавтоколебательныхсистемахтакжемогутнаблюдаться явлениядинамическогохаоса. Длясвязанныхавтоколебательныхсистемхарактернытакие явления, какконкуренциячастотизахватчастоты. Впервыеэто явлениезаметилинесколькостолетийназад, когданесколько маятниковыхчасов, которыешлинемногопоразному(одничуть отставали, другиечутьбежаливперед), поставилинаодин деревянныйприлавоквмагазине. Черезнесколькочасов продавецзаметил, чтовсечасыначалиидтисодинаковой скоростью. Поэтому, еслиувсехэтихчасоввыставитьодноито жевремя, тотеперьниктонебудетотставатьилибежатьвперед.

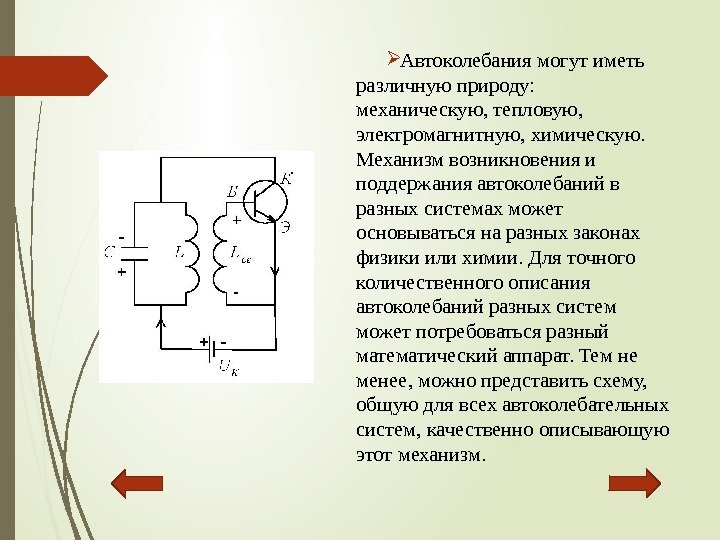
Автоколебаниямогутиметь различнуюприроду: механическую, тепловую, электромагнитную, химическую. Механизмвозникновенияи поддержанияавтоколебанийв разныхсистемахможет основыватьсянаразныхзаконах физикиилихимии. Дляточного количественногоописания автоколебанийразныхсистем можетпотребоватьсяразный математическийаппарат. Темне менее, можнопредставитьсхему, общуюдлявсехавтоколебательных систем, качественноописывающую этотмеханизм.

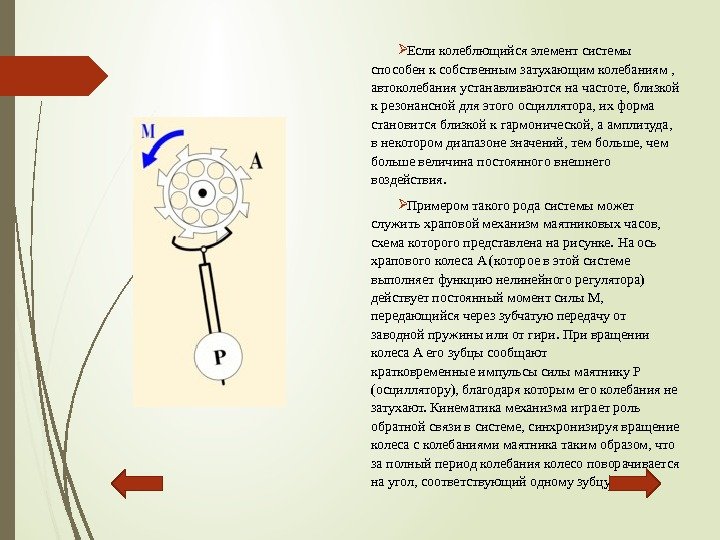
Есликолеблющийсяэлементсистемы способенксобственнымзатухающимколебаниям, автоколебанияустанавливаютсяначастоте, близкой крезонанснойдляэтогоосциллятора, ихформа становитсяблизкойкгармонической, аамплитуда, внекоторомдиапазонезначений, тембольше, чем большевеличинапостоянноговнешнего воздействия. Примеромтакогородасистемыможет служитьхраповоймеханизммаятниковыхчасов, схемакоторогопредставленанарисунке. Наось храповогоколеса. A(котороевэтойсистеме выполняетфункциюнелинейногорегулятора) действуетпостоянныймоментсилы. M, передающийсячереззубчатуюпередачуот заводнойпружиныилиотгири. Привращении колеса. Aегозубцысообщают кратковременныеимпульсысилымаятнику. P (осциллятору), благодарякоторымегоколебанияне затухают. Кинематикамеханизмаиграетроль обратнойсвязивсистеме, синхронизируявращение колесасколебаниямимаятникатакимобразом, что заполныйпериодколебанияколесоповорачивается наугол, соответствующийодномузубцу.

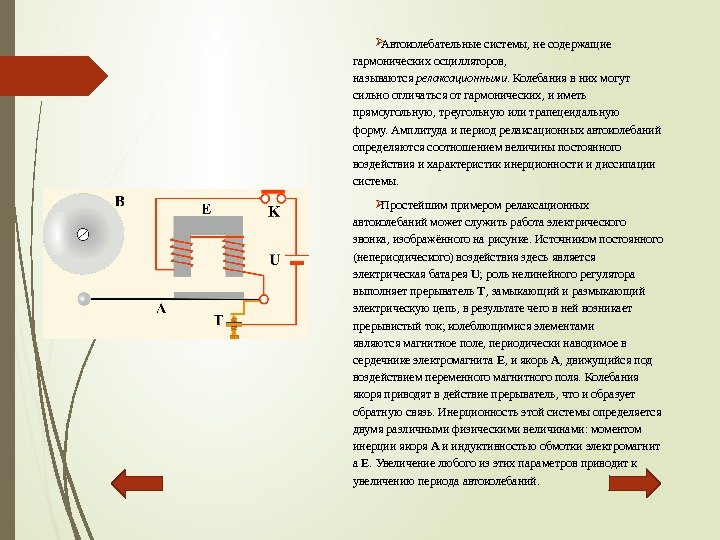
Автоколебательныесистемы, несодержащие гармоническихосцилляторов, называются релаксационными. Колебаниявнихмогут сильноотличатьсяотгармонических, ииметь прямоугольную, треугольнуюилитрапецеидальную форму. Амплитудаипериодрелаксационныхавтоколебаний определяютсясоотношениемвеличиныпостоянного воздействияихарактеристикинерционностиидиссипации системы. Простейшимпримеромрелаксационных автоколебанийможетслужитьработаэлектрического звонка, изображённогонарисунке. Источникомпостоянного (непериодического)воздействияздесьявляется электрическаябатарея U ; рольнелинейногорегулятора выполняетпрерыватель T , замыкающийиразмыкающий электрическуюцепь, врезультатечеговнейвозникает прерывистыйток; колеблющимисяэлементами являютсямагнитноеполе, периодическинаводимоев сердечникеэлектромагнита E , иякорь A , движущийсяпод воздействиемпеременногомагнитногополя. Колебания якоряприводятвдействиепрерыватель, чтоиобразует обратнуюсвязь. Инерционностьэтойсистемыопределяется двумяразличнымифизическимивеличинами: моментом инерцииякоря А ииндуктивностьюобмоткиэлектромагнит а E. Увеличениелюбогоизэтихпараметровприводитк увеличениюпериодаавтоколебаний.

Молоток Маклакова Молоток, совершающийударызасчётэнергии электрическойцепипеременноготокасчастотой, вомного разменьшейчастотытокавцепи. Катушка. Lколебательногоконтурапомещаетсянад столом. Снизувнеёвходитжелезнаятрубка, нижнийконец которойявляетсяударнойчастьюмолотка. Параметры колебательногоконтуратакие, чтособственнаячастотаего колебанийсовпадаетсчастотойтокавцепи. Послевключениятокаиустановленияколебаний наблюдаетсярезонанстоковконтураивнешнейцепи, и железнаятрубкавтягиваетсявкатушку. Индуктивность катушкирастёт, колебательныйконтурвыходитизрезонанса, аамплитудаколебанийтокавкатушкеуменьшается. Поэтому трубкавозвращаетсявисходноеположение-внекатушки- поддействиемсилытяжести. Затемколебаниятокавнутри контураначинаютнарастать, иснованаступаетрезонанс: трубкаопятьвтягиваетсявкатушку. Трубка совершает автоколебания , т. е. периодическиедвижения вверхивниз, иприэтомгромкостучитпостолу, подобно молотку. Периодэтихмеханическихавтоколебанийвдесятки разпревосходитпериодпеременноготока, поддерживающегоих.

Всильнонелинейныхколебательныхсистемахс двумяиболеестепенямисвободыможет происходитьстохастизацияколебаний. Длявнешнего наблюдателятакаяхаотизациясвободныхколебаний выглядиттак, словносистемасовершаетнекоторые случайныедвижения. Разногородаавтокорреляционные функцииикоэффициентыкорреляцийтакогодвижения могутничемнеотличатьсяотдействительнохаотического движенияподдействиемслучайныхвнешнихсил. Хотя всясистемаявляетсязамкнутойидвижетсяподдействием строгихдинамическихзаконов(например, вмеханикепод действиемстрогихзаконов. Ньютона).

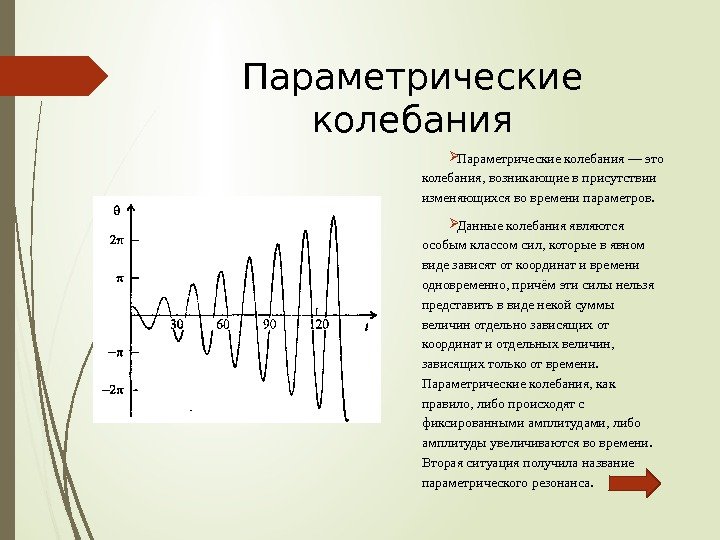
Параметрические колебания Параметрическиеколебания—это колебания, возникающиевприсутствии изменяющихсявовременипараметров. Данныеколебанияявляются особымклассомсил, которыевявном видезависятоткоординативремени одновременно, причёмэтисилынельзя представитьввиденекойсуммы величинотдельнозависящихот координатиотдельныхвеличин, зависящихтолькоотвремени. Параметрическиеколебания, как правило, либопроисходятс фиксированнымиамплитудами, либо амплитудыувеличиваютсявовремени. Втораяситуацияполучиланазвание параметрическогорезонанса.

Параметрические колебания имеют вид: В простейшем случае, для системы с одной степенью свободы для малых отклонений от положения равновесия обобщённая сила такого типа определяется уравнением: Q=-kq=-k(t)q, где k(t) − коэффициент упругости, зависящей от времени. В этом случае дифференциальное уравнение движения представится в виде: Где − обобщённая масса. Поделим предыдущее уравнение на обобщённую массу где ψ(t) − переменный коэффициент. s. . . 3, 2, 1 j), t, q, . . . q, q(QQs 21 jj ~ m 0ψ(t)qqq m )t(k q. . ~. . 0 q)t(kqm. . ~

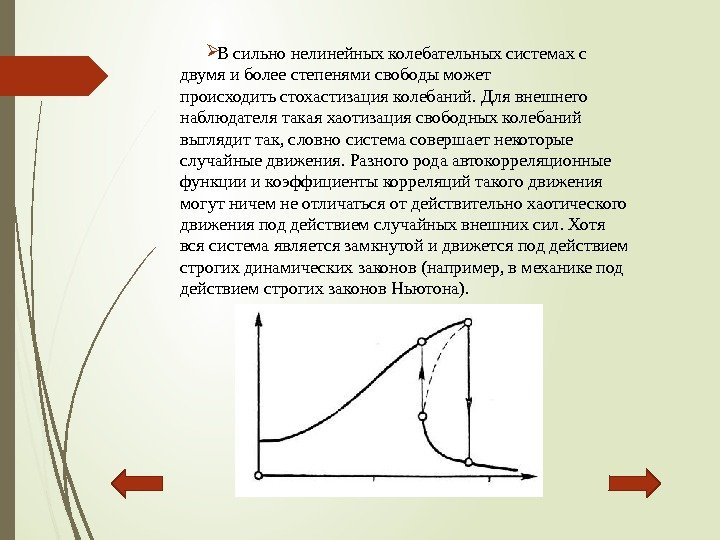
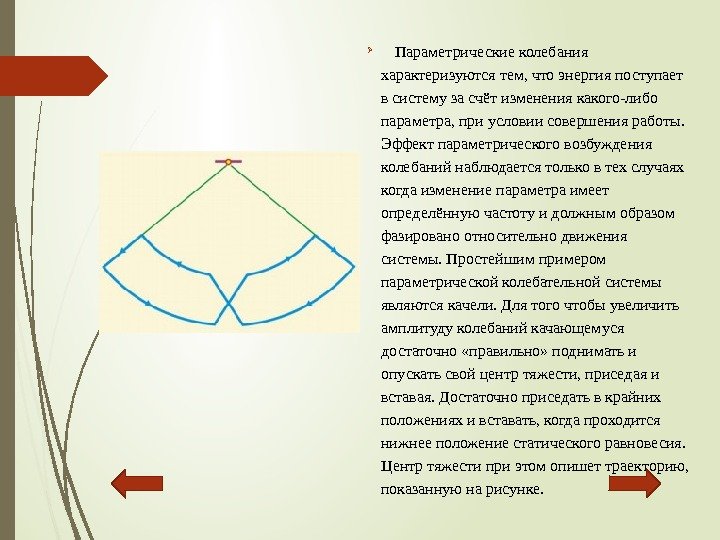
Параметрическиеколебания характеризуютсятем, чтоэнергияпоступает всистемузасчётизменениякакого-либо параметра, приусловиисовершенияработы. Эффектпараметрическоговозбуждения колебанийнаблюдаетсятольковтехслучаях когдаизменениепараметраимеет определённуючастотуидолжнымобразом фазированоотносительнодвижения системы. Простейшимпримером параметрическойколебательнойсистемы являютсякачели. Длятогочтобыувеличить амплитудуколебанийкачающемуся достаточно «правильно» подниматьи опускатьсвойцентртяжести, приседаяи вставая. Достаточноприседатьвкрайних положенияхивставать, когдапроходится нижнееположениестатическогоравновесия. Центртяжестиприэтомопишеттраекторию, показаннуюнарисунке.

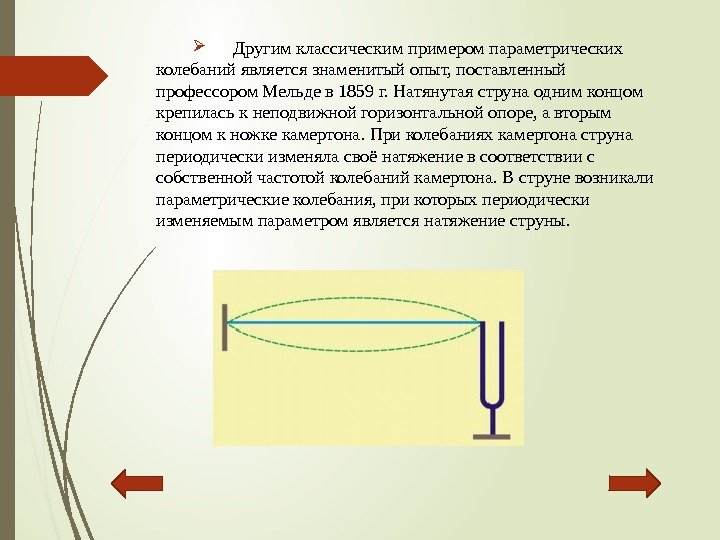
Другимклассическимпримеромпараметрических колебанийявляетсязнаменитыйопыт, поставленный профессором. Мельдев 1859 г. Натянутаяструнаоднимконцом крепиласькнеподвижнойгоризонтальнойопоре, авторым концомкножкекамертона. Приколебанияхкамертонаструна периодическиизменяласвоёнатяжениевсоответствиис собственнойчастотойколебанийкамертона. Вструневозникали параметрическиеколебания, прикоторыхпериодически изменяемымпараметромявляетсянатяжениеструны.

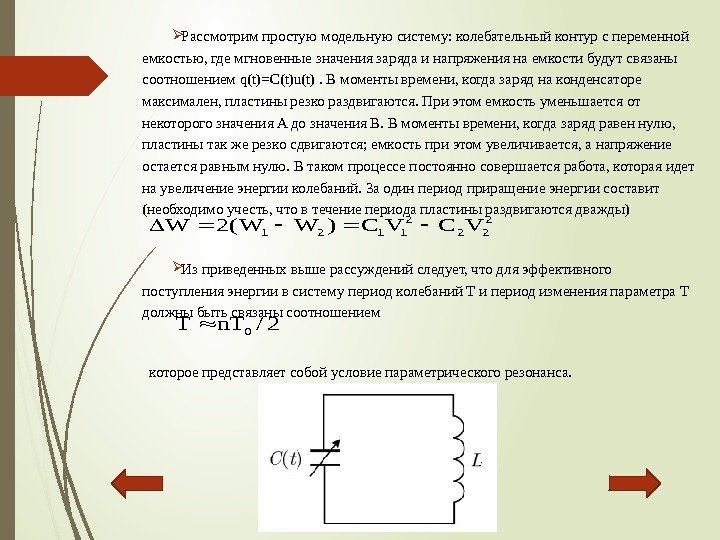
Рассмотримпростуюмодельнуюсистему: колебательныйконтурспеременной емкостью, гдемгновенныезначениязарядаинапряжениянаемкостибудутсвязаны соотношениемq(t)=C(t)u(t). Вмоментывремени, когдазаряднаконденсаторе максимален, пластинырезкораздвигаются. Приэтомемкостьуменьшаетсяот некоторогозначения. Aдозначения. B. Вмоментывремени, когдазарядравеннулю, пластинытакжерезкосдвигаются; емкостьприэтомувеличивается, анапряжение остаетсяравнымнулю. Втакомпроцессепостоянносовершаетсяработа, котораяидет наувеличениеэнергииколебаний. Заодинпериодприращениеэнергиисоставит (необходимоучесть, чтовтечениепериодапластиныраздвигаютсядважды) Изприведенныхвышерассужденийследует, чтодляэффективного поступленияэнергиивсистемупериодколебаний. Tипериодизмененияпараметра. T должныбытьсвязанысоотношением котороепредставляетсобойусловиепараметрическогорезонанса. 2 22 2 1121 VCVC)WW(2 W 2/n. TT

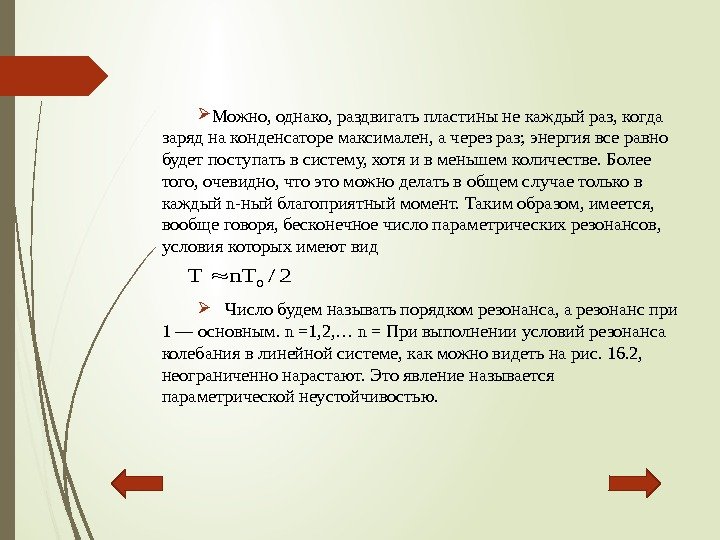
Можно, однако, раздвигатьпластинынекаждыйраз, когда заряднаконденсаторемаксимален, ачерезраз; энергиявсеравно будетпоступатьвсистему, хотяивменьшемколичестве. Более того, очевидно, чтоэтоможноделатьвобщемслучаетольков каждыйn-ныйблагоприятныймомент. Такимобразом, имеется, вообщеговоря, бесконечноечислопараметрическихрезонансов, условиякоторыхимеютвид Числобудемназыватьпорядкомрезонанса, арезонанспри 1—основным. n=1, 2, …n=Привыполненииусловийрезонанса колебаниявлинейнойсистеме, какможновидетьнарис. 16. 2, неограниченнонарастают. Этоявлениеназывается параметрическойнеустойчивостью. 2/n. TT