Коды Рида-Малера Матричные коды Коды Рида-Маллера

Коды Рида-Малера

Матричные коды • Коды Рида-Маллера относятся к так называемым матричным кодам, широко применяемым в теории кодирования. • Общая идея матричных кодов – умножение двоичной строки на фиксированную матрицу А – так называемую производящую матрицу кода.

Создатели кода • Ирвинг Рид (1923 -2012) – американский математик и инженер. Соавтор знаменитых кодов Рида-Маллера и Рида-Соломона. • Дэвид Маллер (1924 – 2008) американский математик и специалист по компьютерным технологиям.

Характеристики кодов Рида-Маллера n=2 m – длина кода; – количество информационных разрядов; – минимальное кодовое расстояние; где δ < m – порядок кода R=r/n – значение избыточности (r=n-k) – переменное; dmin – минимальное кодовое расстояние – переменная величина (2, 4, 8); 1

Пример Пусть m=4, тогда δ может принимать значения δ =1, 2, 3. Для δ=1 находим: n=24=16, d=24 -1=8, k= 1+4=5; r=n-k=16 -5=11; R=r/n=11/16≈0, 7. Для δ=2 n=24=16, d=24 -2=4, k= =1+4+6=11; r=nk=16 -11=5; R=r/n=5/16 ≈0, 312. Для δ=3 n=24=16, d=24 -3=2, k= =1+4+6+4=15; r=nk=16 -15=1; R=r/n=1/16≈ 0, 07. Таким образом, можно получить коды Рида. Маллера размеров (16, 5), (16, 11) и (16, 15) и другие. 2

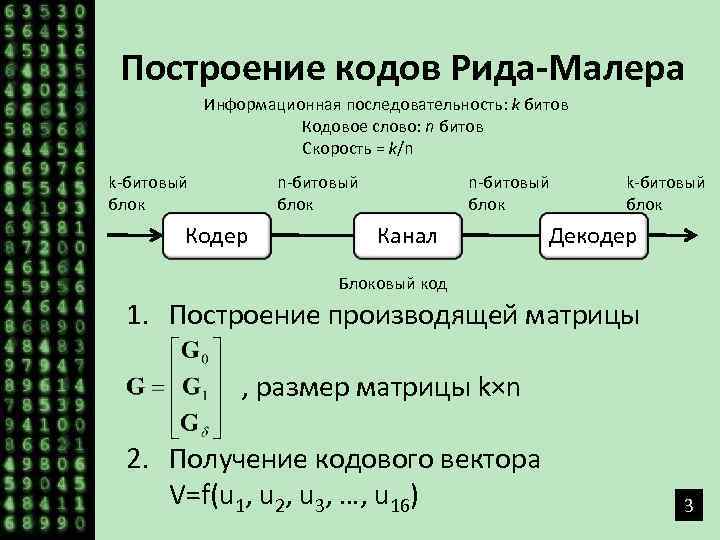Построение кодов Рида-Малера Информационная последовательность: k битов Кодовое слово: n битов Скорость = k/n k-битовый блок n-битовый блок Кодер n-битовый блок Канал k-битовый блок Декодер Блоковый код 1. Построение производящей матрицы , размер матрицы k×n 2. Получение кодового вектора V=f(u 1, u 2, u 3, …, u 16) 3

Построение производящей матрицы G (16, 11) -код второго порядка (δ=2) для m=4 G= 11111111 01010101 00110011 00001111 00010001 00000101 000000110011 0000001111 4

Значения кодового вектора 5

Декодирование Общий принцип поиска проверочных соотношений заключается в нахождении таких совокупностей столбцов, сумма которых по модулю два будет содержать только одну единицу в разряде, соответствующему отыскиваемому uki. Местоположение столбцов указывает, какие ui входят в данное соотношение. В общем случае для каждого uki должно быть не менее 2 m-δ независимых уравнений. 6

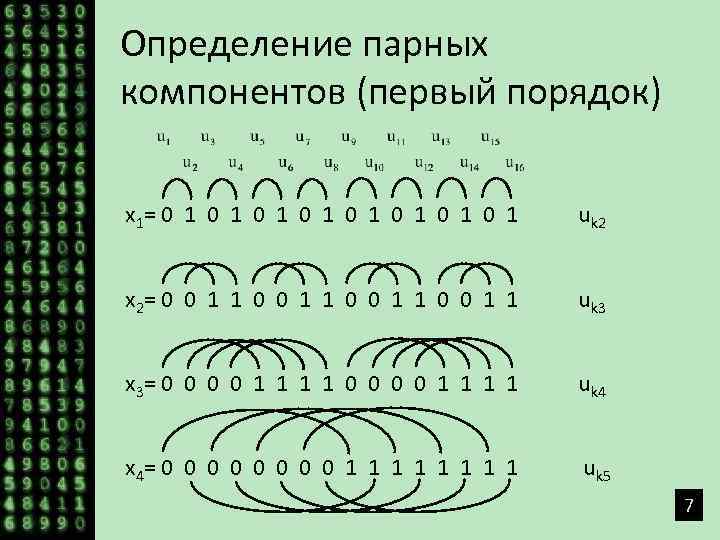Определение парных компонентов (первый порядок) x 1 = 0 1 0 1 uk 2 x 2 = 0 0 1 1 uk 3 x 3 = 0 0 0 0 1 1 1 1 uk 4 x 4 = 0 0 0 0 1 1 1 1 uk 5 7

Уравнения первого порядка 8

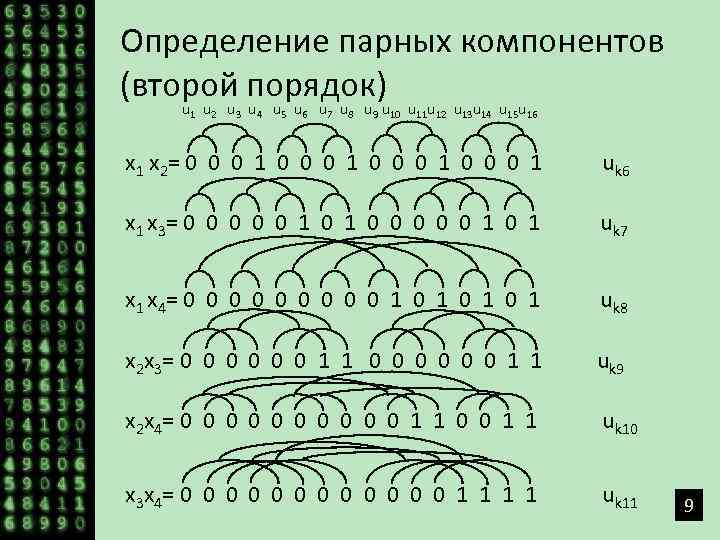Определение парных компонентов (второй порядок) u 1 u 2 u 3 u 4 u 5 u 6 u 7 u 8 u 9 u 10 u 11 u 12 u 13 u 14 u 15 u 16 x 1 x 2 = 0 0 0 1 uk 6 x 1 x 3 = 0 0 0 0 0 1 0 1 uk 7 x 1 x 4 = 0 0 0 0 0 1 0 1 uk 8 x 2 x 3 = 0 0 0 1 1 uk 9 x 2 x 4 = 0 0 0 0 0 1 1 uk 10 x 3 x 4 = 0 0 0 1 1 uk 11 9

Уравнения второго порядка 10

Исправление ошибок. Критерий большинства проверок Каждый uki описывается d=2 m-δ уравнениями; Из d уравнений получаем uk 1, uk 2, uk 3, … ukd значений uki Их арифметическая сумма , если все уравнения дают uki=0; , если все уравнения дают uki=1. При наличии ошибок критерий большинства имеет вид: uki=0, если Uki неизвестно, если ; uki=1, если ; . 11

Пример. Кодирование uk 1 uk 2 uk 3 uk 4 uk 5 uk 6 uk 7 uk 8 uk 9 uk 10 uk 11 Исходное сообщение: Кодовый вектор: 0 1 0 0 0 1 1 1 1 0 0 1 1 0 u 1 u 2 u 3 u 4 u 5 u 6 u 7 u 8 u 9 u 10 u 11 u 12 u 13 u 14 u 15 u 16 12

Пример. Декодирование u 1 u 2 u 3 u 4 u 5 u 6 u 7 u 8 u 9 u 10 u 11 u 12 u 13 u 14 u 15 u 16 Получено сообщение: 1 1 1 0 0 Декодирование сообщения : _ _ _ 0 1 1 uk 2 uk 3 uk 4 uk 5 uk 6 uk 7 uk 8 uk 9 uk 10 uk 11 13

Пример. Преобразование u 1 u 2 u 3 u 4 u 5 u 6 u 7 u 8 u 9 u 10 u 11 u 12 u 13 u 14 u 15 u 16 Получено сообщение: 1 1 1 0 0 Декодирование сообщения: _ _ _ 0 1 1 uk 2 uk 3 uk 4 uk 5 uk 6 uk 7 uk 8 uk 9 uk 10 uk 11 1 1 0 1 0 0 1 1 0 0 – принятое сообщение 0 0 0 1 1 – uk 11 x 3 x 4 0 0 0 0 0 1 1 – uk 10 x 2 x 4 0 0 0 0 0 1 0 1 – uk 8 x 1 x 4 0 0 0 0 0 1 0 1 – uk 7 x 1 x 3 1 1 1 1 0 0 0 0 – преобразованное сообщение 14

Пример. Декодирование (2) u 1 u 2 u 3 u 4 u 5 u 6 u 7 u 8 u 9 u 10 u 11 u 12 u 13 u 14 u 15 u 16 Получено сообщение: 1 1 1 0 0 Декодирование сообщения : Преобразованное сообщение: uk 1 uk 2 uk 3 uk 4 uk 5 uk 6 uk 7 uk 8 uk 9 uk 10 uk 11 _ _ _ 0 1 1 u 1 u 2 u 3 u 4 u 5 u 6 u 7 u 8 u 9 u 10 u 11 u 12 u 13 u 14 u 15 u 16 1 1 1 1 0 0 0 0 Декодирование сообщения : _ 0 0 0 1 1 uk 2 uk 3 uk 4 uk 5 uk 6 uk 7 uk 8 uk 9 uk 10 uk 11 15

Пример. Преобразование (2) u 1 u 2 u 3 u 4 u 5 u 6 u 7 u 8 u 9 u 10 u 11 u 12 u 13 u 14 u 15 u 16 Получено сообщение: 1 1 1 0 0 Преобразованное u 1 u 2 u 3 u 4 u 5 u 6 u 7 u 8 u 9 u 10 u 11 u 12 u 13 u 14 u 15 u 16 сообщение: 1 1 1 1 0 0 0 0 Декодирование сообщения : uk 1 uk 2 uk 3 uk 4 uk 5 uk 6 uk 7 uk 8 uk 9 uk 10 uk 11 _ 0 0 0 1 1 1 1 1 0 0 0 0 – преобразованное сообщение 0 0 0 0 1 1 1 1 – uk 5 x 4 1 1 1 1 – преобразованное сообщение (2) uk 1=1, если вектор (2) содержит все единицы uk 1=0, если вектор (2) содержит все нули Декодированное сообщение : 1 0 0 0 1 1 uk 2 uk 3 uk 4 uk 5 uk 6 uk 7 uk 8 uk 9 uk 10 uk 11 16

Спасибо за внимание!