Классификация связей. Принцип возможных перемещений. ЛЕКЦИИ ПО















lekciya_dinamika_11.pptx
- Размер: 985.0 Кб
- Автор:
- Количество слайдов: 20
Описание презентации Классификация связей. Принцип возможных перемещений. ЛЕКЦИИ ПО по слайдам
 Классификация связей. Принцип возможных перемещений. ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. ДИНАМИКА
Классификация связей. Принцип возможных перемещений. ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. ДИНАМИКА
 • Рассмотреть классификацию связей в динамике, познакомиться с принципом возможных перемещений и научиться с помощью этого принципа решать задачи статики. ПЛАН ЛЕКЦИИ • Классификация связей; • Принцип возможных перемещений; • Решение задач; • Заключение. 2 ЦЕЛЬ ЛЕКЦИИ
• Рассмотреть классификацию связей в динамике, познакомиться с принципом возможных перемещений и научиться с помощью этого принципа решать задачи статики. ПЛАН ЛЕКЦИИ • Классификация связей; • Принцип возможных перемещений; • Решение задач; • Заключение. 2 ЦЕЛЬ ЛЕКЦИИ
 В статике: Связи — то, что не даёт перемещаться • Действие связей описывается реакциями. В аналитической механике: Связи — любого вида ограничения, которые налагаются на положение и скорость движущихся тел (точек). • Действие связи описывается уравнениями (или неравенствами), которые определяют ограничения на движение тел. 3 СВЯЗИ 3 Классификация связей
В статике: Связи — то, что не даёт перемещаться • Действие связей описывается реакциями. В аналитической механике: Связи — любого вида ограничения, которые налагаются на положение и скорость движущихся тел (точек). • Действие связи описывается уравнениями (или неравенствами), которые определяют ограничения на движение тел. 3 СВЯЗИ 3 Классификация связей
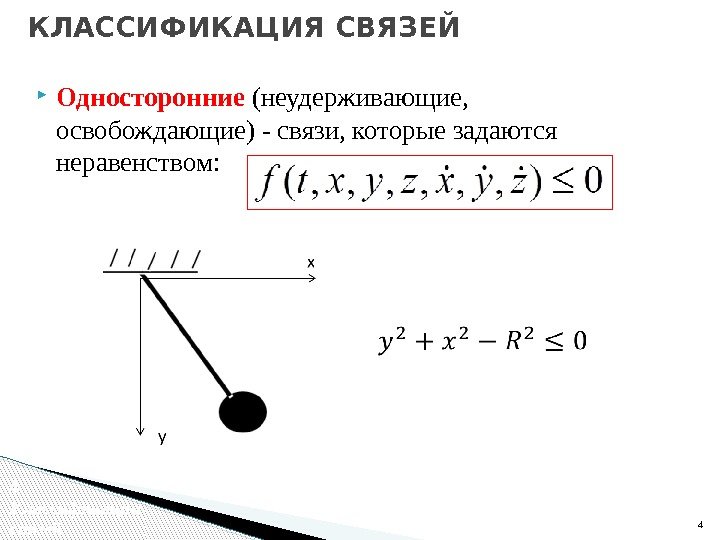
 Односторонние (неудерживающие, освобождающие) — связи, которые задаются неравенством: 4 КЛАССИФИКАЦИЯ СВЯЗЕЙ 4 Классификация связей
Односторонние (неудерживающие, освобождающие) — связи, которые задаются неравенством: 4 КЛАССИФИКАЦИЯ СВЯЗЕЙ 4 Классификация связей
 Двусторонние (удерживающие, неосвобождающие) – связи, которые задаются уравнением: 5 КЛАССИФИКАЦИЯ СВЯЗЕЙ 5 Классификация связей
Двусторонние (удерживающие, неосвобождающие) – связи, которые задаются уравнением: 5 КЛАССИФИКАЦИЯ СВЯЗЕЙ 5 Классификация связей
 Стационарные связи — связи, уравнения которых не содержат времени в явном виде: 6 КЛАССИФИКАЦИЯ СВЯЗЕЙ 6 Классификация связей
Стационарные связи — связи, уравнения которых не содержат времени в явном виде: 6 КЛАССИФИКАЦИЯ СВЯЗЕЙ 6 Классификация связей
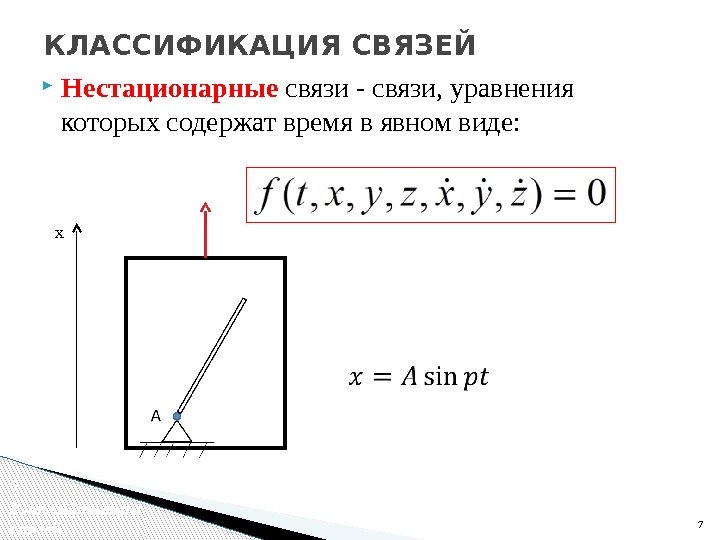
 Нестационарные связи — связи, уравнения которых содержат время в явном виде: 7 КЛАССИФИКАЦИЯ СВЯЗЕЙ x 7 Классификация связей
Нестационарные связи — связи, уравнения которых содержат время в явном виде: 7 КЛАССИФИКАЦИЯ СВЯЗЕЙ x 7 Классификация связей
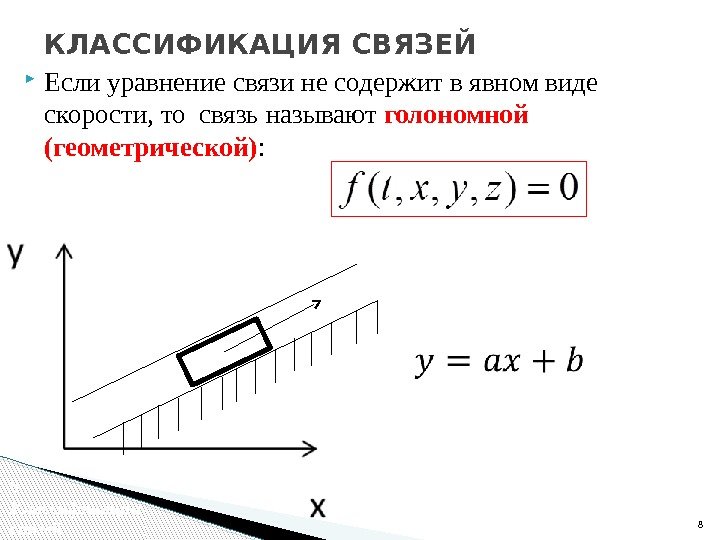
 Если уравнение связи не содержит в явном виде скорости, то связь называют голономной (геометрической) : 8 КЛАССИФИКАЦИЯ СВЯЗЕЙ 8 Классификация связей
Если уравнение связи не содержит в явном виде скорости, то связь называют голономной (геометрической) : 8 КЛАССИФИКАЦИЯ СВЯЗЕЙ 8 Классификация связей
 Если уравнение связи содержит в явном виде скорость, то связь называют неголономной : 9 КЛАССИФИКАЦИЯ СВЯЗЕЙ A 9 Классификация связей
Если уравнение связи содержит в явном виде скорость, то связь называют неголономной : 9 КЛАССИФИКАЦИЯ СВЯЗЕЙ A 9 Классификация связей
 10 ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 10 Принцип возможных перемещений
10 ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 10 Принцип возможных перемещений
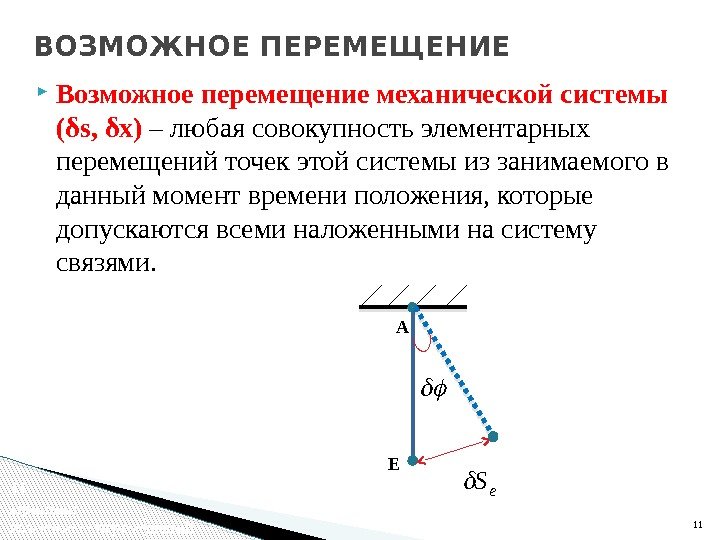
 Возможное перемещение механической системы (δs, δx) – любая совокупность элементарных перемещений точек этой системы из занимаемого в данный момент времени положения, которые допускаются всеми наложенными на систему связями. 11 ВОЗМОЖНОЕ ПЕРЕМЕЩЕНИЕ А Е 11 Принцип возможных перемещенийe. S
Возможное перемещение механической системы (δs, δx) – любая совокупность элементарных перемещений точек этой системы из занимаемого в данный момент времени положения, которые допускаются всеми наложенными на систему связями. 11 ВОЗМОЖНОЕ ПЕРЕМЕЩЕНИЕ А Е 11 Принцип возможных перемещенийe. S
 Возможные перемещения характеризуются тем, что они: • могут и не происходить (они воображаемые); • бесконечно малые; • происходят с сохранением всех наложенных на систему связей; • не связаны с реальным времененм (δt = 0). Для стационарных связей действительное перемещение dr можно представить как набор возможных 12 ВОЗМОЖНОЕ ПЕРЕМЕЩЕНИЕ 12 Принцип возможных перемещений
Возможные перемещения характеризуются тем, что они: • могут и не происходить (они воображаемые); • бесконечно малые; • происходят с сохранением всех наложенных на систему связей; • не связаны с реальным времененм (δt = 0). Для стационарных связей действительное перемещение dr можно представить как набор возможных 12 ВОЗМОЖНОЕ ПЕРЕМЕЩЕНИЕ 12 Принцип возможных перемещений
 Возможная работа – это элементарная работа, которую действующая на материальную точку сила могла бы совершить на перемещении, совпадающем с возможным перемещением этой точки: Связи, сумма возможных работ реакций которых на любом возможном перемещении равна нулю, называются идеальными связями : 13 ВОЗМОЖНАЯ РАБОТА 13 Принцип возможных перемещений
Возможная работа – это элементарная работа, которую действующая на материальную точку сила могла бы совершить на перемещении, совпадающем с возможным перемещением этой точки: Связи, сумма возможных работ реакций которых на любом возможном перемещении равна нулю, называются идеальными связями : 13 ВОЗМОЖНАЯ РАБОТА 13 Принцип возможных перемещений
 Устанавливает общее условие равновесия механической системы в целом При идеальных связях позволяет исключить из рассмотрения все неизвестные реакции связей Выполняется в инерциальных системах отсчета 14 ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 14 Принцип возможных перемещений
Устанавливает общее условие равновесия механической системы в целом При идеальных связях позволяет исключить из рассмотрения все неизвестные реакции связей Выполняется в инерциальных системах отсчета 14 ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 14 Принцип возможных перемещений
 — возможная работа активной силы. 15 ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на неё активных сил при любом возможном перемещении системы была равна нулю. 15 Принцип возможных перемещений
— возможная работа активной силы. 15 ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на неё активных сил при любом возможном перемещении системы была равна нулю. 15 Принцип возможных перемещений
 Необходимость: Пусть механическая система находится под действием внешних активных сил, главный вектор которых: На неё наложены голономные, стационарные связи: Тогда, поскольку каждая из точек системы находится в равновесии: Просуммируем по всем точкам системы: По определению идеальных связей: 16 16 Принцип возможных перемещений
Необходимость: Пусть механическая система находится под действием внешних активных сил, главный вектор которых: На неё наложены голономные, стационарные связи: Тогда, поскольку каждая из точек системы находится в равновесии: Просуммируем по всем точкам системы: По определению идеальных связей: 16 16 Принцип возможных перемещений
 Достаточность: Пусть механическая система с идеальными связями, удовлетворяющая неравенству совершает действительное перемещение Тогда: d. T = При стационарных связях действительные перемещения совпадают с какими-либо возможными перемещениями: Но это противоречит условию: 17 Когда приложенные силы к системе удовлетворяют этому условию, система из состояния покоя выйти не может, следовательно, это условие является достаточным условием равновесия системы. 17 Принцип возможных перемещений
Достаточность: Пусть механическая система с идеальными связями, удовлетворяющая неравенству совершает действительное перемещение Тогда: d. T = При стационарных связях действительные перемещения совпадают с какими-либо возможными перемещениями: Но это противоречит условию: 17 Когда приложенные силы к системе удовлетворяют этому условию, система из состояния покоя выйти не может, следовательно, это условие является достаточным условием равновесия системы. 17 Принцип возможных перемещений
 Пример: Найти величину силы Р, удерживающей тяжелые гладкие призмы с массами m 1 m 2 в состоянии равновесия. Угол скоса призм равен α. 18 РЕШЕНИЕ ЗАДАЧ + 18 Решение задач
Пример: Найти величину силы Р, удерживающей тяжелые гладкие призмы с массами m 1 m 2 в состоянии равновесия. Угол скоса призм равен α. 18 РЕШЕНИЕ ЗАДАЧ + 18 Решение задач
 Принцип возможных перемещений позволяет решать самые разнообразные задачи на равновесие механических систем – находить неизвестные активные силы , определять реакции связей , находить положения равновесия механической системы под действием приложенной системы сил. 1919 Решение задач
Принцип возможных перемещений позволяет решать самые разнообразные задачи на равновесие механических систем – находить неизвестные активные силы , определять реакции связей , находить положения равновесия механической системы под действием приложенной системы сил. 1919 Решение задач
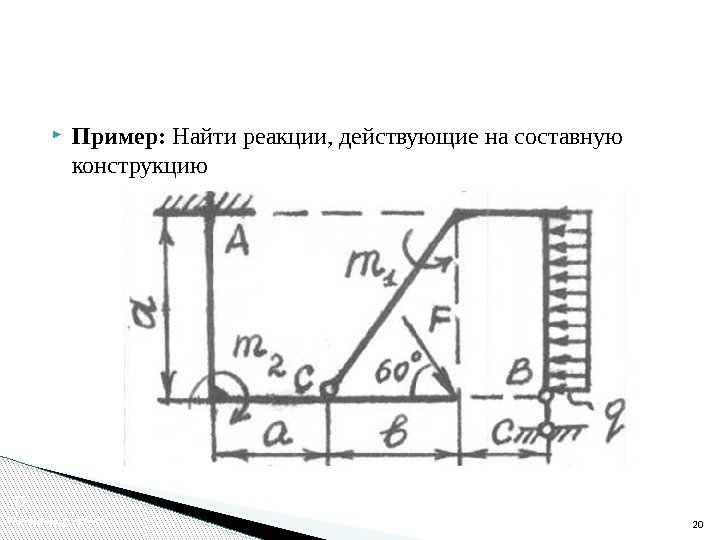
 Пример: Найти реакции, действующие на составную конструкцию 2020 Решение задач
Пример: Найти реакции, действующие на составную конструкцию 2020 Решение задач
