Интегрирование рациональных функций Дробно – рациональная функция Простейшие

Интегрирование рациональных функций Дробно – рациональная функция Простейшие рациональные дроби Разложение рациональной дроби на простейшие дроби Интегрирование простейших дробей Общее правило интегрирования рациональных дробей

многочлен степени n. Дробно – рациональная функция Дробно – рациональной функцией называется функция, равная отношению двух многочленов: Рациональная дробь называется правильной , если степень числителя меньше степени знаменателя, то есть m < n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби: )( )( )( x. Q x. P xf n m )( )( )( x. Q x. R x. L x. Q x. P

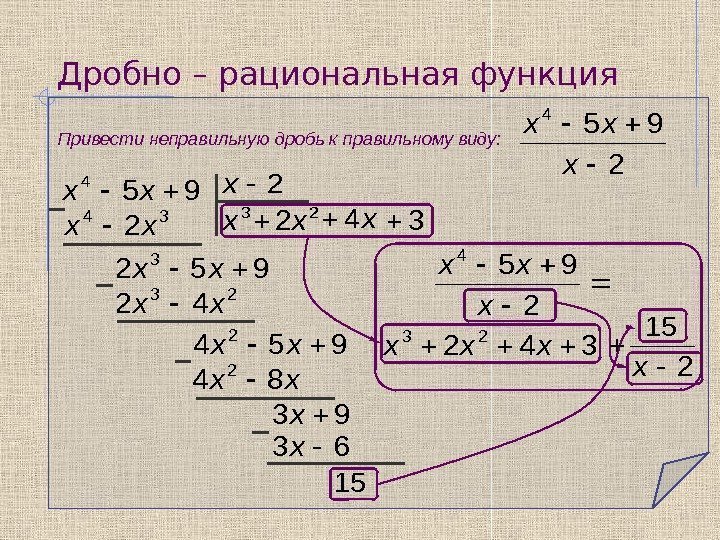
Дробно – рациональная функция Привести неправильную дробь к правильному виду: 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 93 x 3 63 x 15 2 95 4 x xx 342 23 xxx 2 15 x

Простейшие рациональные дроби Правильные рациональные дроби вида: Называются простейшими рациональными дробями типов. ax A ); 2(Nkk ax A k )04( 2 2 qp qpxx NMx ); 2; 04( 2 2 Nkkqp qpxx NMx k V V, , ,

Разложение рациональной дроби на простейшие дроби Теорема : Всякую правильную рациональную дробь , знаменатель которой разложен на множители: можно представить, притом единственным образом в виде суммы простейших дробей: s k qxpxxxxxx. Q )( )()( 22 2 11 2 21 )( )( x. Q x. P 1 xx A k k xx B )()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11 )(qxpx Nx. M s ss qxpx Nx. M )(

Разложение рациональной дроби на простейшие дроби Поясним формулировку теоремы на следующих примерах: Для нахождения неопределенных коэффициентов A, B, C, D … применяют два метода: метод сравнивания коэффициентов и метод частных значений переменной. Первый метод рассмотрим на примере. 3 2 )3)(2( 4 xx x 2 x A 3 3 2 21 )3()3(3 x B x B 1 2 x DCx 22 22 2 11 )1(1 xx Nx. M )1( 3 22 3 xx x 2 21 x A 22 2 )1)(4( 987 xxx xx 4 x

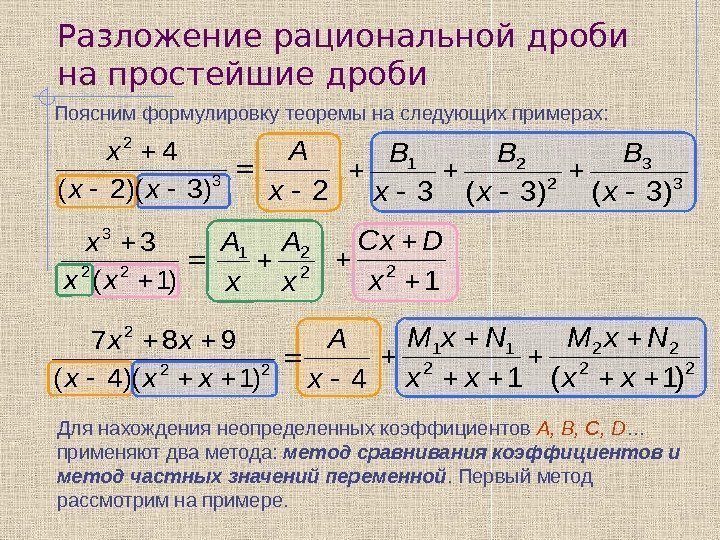
Разложение рациональной дроби на простейшие дроби Представить дробь в виде суммы простейших дробей: Приведем простейшие дроби к общему знаменателю Приравняем числители получившейся и исходной дробей Приравняем коэффициенты при одинаковых степенях х)52)(1( 332 2 2 xxx xx 1 x A 52 2 xx CBx )52)(1( )1)(()52( 2 2 xxx x. CBxxx. A 33252 222 xx. CBx. Cx. Bx. AAx. Ax 35 32 2 0 1 2 CAx BAx 2 3 1 C B A 52 23 1 1 2 xx x x

Интегрирование простейших дробей Найдем интегралы от простейших рациональных дробей: Интегрирование дроби 3 типа рассмотрим на примере. dx ax A k dx qpxx NMx 2 ax axd A )( Cax. Aln )(axdax. A k C k ax. A k

Интегрирование простейших дробейdx xx x 102 13 2 dx xx x 9)12( 13 2 dx x x 9)1( 13 2 dtdx tx tx 1 1 dt t t 9 1)1(3 2 dt t t 9 23 2 9 322 t dtt 9 9 2 3 2 2 t td 33 2 t arctg. C t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln

Интегрирование простейших дробей Интеграл данного типа с помощью подстановки: приводится к сумме двух интегралов: Первый интеграл вычисляется методом внесения t под знак дифференциала. Второй интеграл вычисляется с помощью рекуррентной формулы: dx qpxx NMx k 2 V t p x 2 kk at dt N at dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt

Интегрирование простейших дробей a = 1; k = 3 323 )1(t dt tarctg t dt 1 21 )1)(12(2222 322 1 21222 t t t dt )1(22 1 2 t t tarctg 2223 )1)(13(2232 332 t t C t t tarctg 222 )1(4)1(

Общее правило интегрирования рациональных дробей Если дробь неправильная, то представить ее в виде суммы многочлена и правильной дроби. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших дробей с неопределенными коэффициентами Найти неопределенные коэффициенты методом сравнения коэффициентов или методом частных значений переменной. Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример Приведем дробь к правильному виду. dx xxx 23 35 2 442 35 xxxxxx 23 2 2 x 345 2 xxx 442 34 xxx x 2 234 242 xxx 4425 23 xxx xxx 23 35 2 442 xxx xx xx 23 2 2 2 48 52 5 xxx 5105 23 48 2 xx

Пример Разложим знаменатель правильной дроби на множители Представим дробь в виде суммы простейших дробей Найдем неопределенные коэффициенты методом частных значений переменной xxx xx 23 2 2 48 2 2 )1( 48 xx xx 2 )1(1 x C x B x A 2 2 )1()1( xx Cxx. Bxx. A 48)1()1( 22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2 )1( 3 1 124 xxx

Пример dx xx 2 2 )1( 3 1 124 52 2 2 )1( 3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln