Глава 4. Введениеванализ § 1. Основныепонятия Числовые






















glava_4-1.ppt
- Размер: 577.5 Кб
- Автор:
- Количество слайдов: 25
Описание презентации Глава 4. Введениеванализ § 1. Основныепонятия Числовые по слайдам
 Глава 4. Введениеванализ § 1. Основныепонятия
Глава 4. Введениеванализ § 1. Основныепонятия
 Числовые промежутки. Окрестность точки
Числовые промежутки. Окрестность точки
 Определение 2. Окрестностью точки x 0 называетсяпроизвольный интервал( a , b ), содержащийэтуточку внутрисебя. • О п р е д е л е н и е 3. Пусть —некоторое положительноечисло. -окрестностьюточки x 0 называетсямножество всехточек x , принадлежащихпромежутку ( x 0 ‑ , x 0 + ). • Принадлежностьточки x ‑ окрестноститочки можновыразитьспомощьюнеравенства x – x 0 < . • Число называетсярадиусомокрестности. X 0 — X 0 + X
Определение 2. Окрестностью точки x 0 называетсяпроизвольный интервал( a , b ), содержащийэтуточку внутрисебя. • О п р е д е л е н и е 3. Пусть —некоторое положительноечисло. -окрестностьюточки x 0 называетсямножество всехточек x , принадлежащихпромежутку ( x 0 ‑ , x 0 + ). • Принадлежностьточки x ‑ окрестноститочки можновыразитьспомощьюнеравенства x – x 0 < . • Число называетсярадиусомокрестности. X 0 — X 0 + X
 Функция
Функция
 Определение 1. Пусть D — некоторое множество чисел. Если задан закон, по которому каждому числу x из множества D ставится в соответствие единственное определенное число y , то будем говорить, что на множестве D задана функция, которую назовём f. • Число y — это значение функции f в точке x , что обозначается формулой y = f(x). • Число x называется аргументом функции • Множество D — областью определения функции • Все значения y образуют множество E , которое называется множеством значений или областью изменения функции.
Определение 1. Пусть D — некоторое множество чисел. Если задан закон, по которому каждому числу x из множества D ставится в соответствие единственное определенное число y , то будем говорить, что на множестве D задана функция, которую назовём f. • Число y — это значение функции f в точке x , что обозначается формулой y = f(x). • Число x называется аргументом функции • Множество D — областью определения функции • Все значения y образуют множество E , которое называется множеством значений или областью изменения функции.

 • Определение 2. Графиком функции называется множество всех точек плоскости, абсциссы которых являются значениями независимой переменной х, а ординаты – соответствующими значениями функции .
• Определение 2. Графиком функции называется множество всех точек плоскости, абсциссы которых являются значениями независимой переменной х, а ординаты – соответствующими значениями функции .
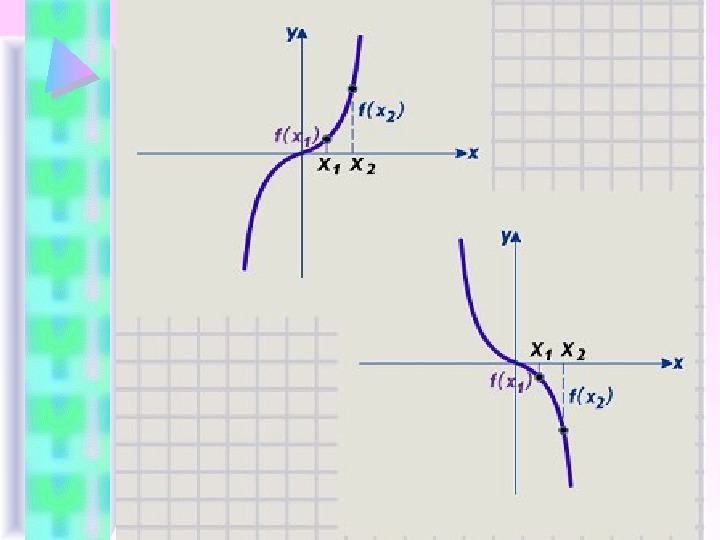
 О п р е д е л е н и е 3. Функция f называется возрастающей (убывающей) на множестве G , если для любых чисел х 1 и х 2 из множества G , таких что x 1 < x 2 , выполняется условие f ( x 1 ) f ( x 2 )). • Функция f называется невозрастающей (неубывающей) на множестве G , если для любых чисел х 1 и х 2 из множества G , таких что x 1 < x 2 , выполняется условие f ( x 1 ) f ( x 2 )( f ( x 1 ) f ( x 2 )).
О п р е д е л е н и е 3. Функция f называется возрастающей (убывающей) на множестве G , если для любых чисел х 1 и х 2 из множества G , таких что x 1 < x 2 , выполняется условие f ( x 1 ) f ( x 2 )). • Функция f называется невозрастающей (неубывающей) на множестве G , если для любых чисел х 1 и х 2 из множества G , таких что x 1 < x 2 , выполняется условие f ( x 1 ) f ( x 2 )( f ( x 1 ) f ( x 2 )).

 Определение 4. Возрастающие, невозрастающие, убывающие, неубывающие функции на множестве G называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными. • Интервалы, вкоторых функциямонотонна, называются интервалами монотонности. • О п р е д е л е н и е 5. Функция f( x ) называется ограниченнойна множестве G, если существует такое число М>0, что x G выполняется неравенство f ( x ) M. • Отсюда следует, что график f ( x ) лежит между прямыми у = — М и у = М. Y X 0 y = — M
Определение 4. Возрастающие, невозрастающие, убывающие, неубывающие функции на множестве G называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными. • Интервалы, вкоторых функциямонотонна, называются интервалами монотонности. • О п р е д е л е н и е 5. Функция f( x ) называется ограниченнойна множестве G, если существует такое число М>0, что x G выполняется неравенство f ( x ) M. • Отсюда следует, что график f ( x ) лежит между прямыми у = — М и у = М. Y X 0 y = — M
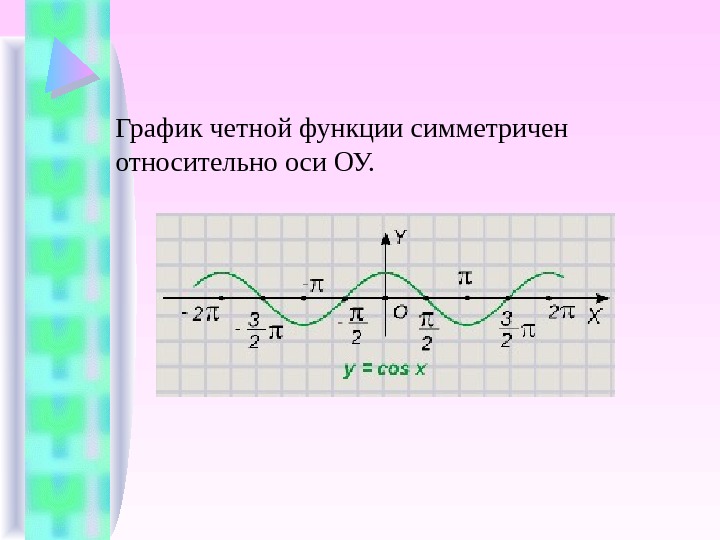
 О п р е д е л е н и е 6. Функция называется четной , если)()(xfxf
О п р е д е л е н и е 6. Функция называется четной , если)()(xfxf
 График четной функции симметричен относительно оси ОУ.
График четной функции симметричен относительно оси ОУ.
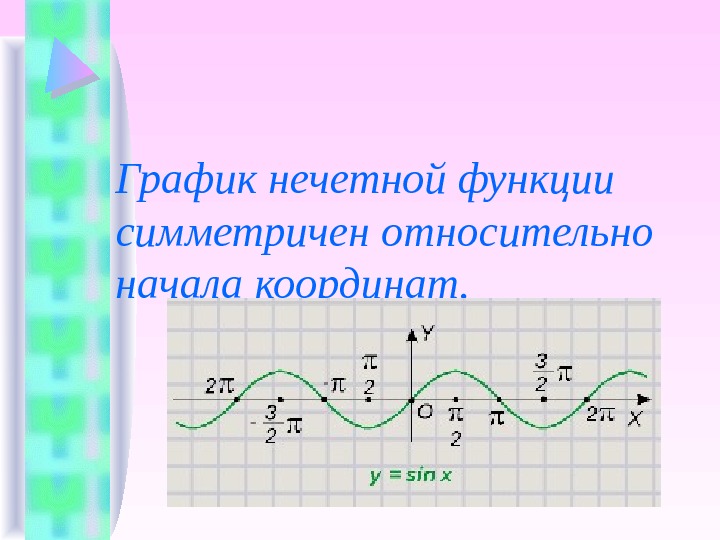
 О п р е д е л е н и е 7. Ф ункция называется нечетной , если )()(xfxf
О п р е д е л е н и е 7. Ф ункция называется нечетной , если )()(xfxf
 График нечетной функции симметричен относительно начала координат.
График нечетной функции симметричен относительно начала координат.
 Определение 8. Функция f ( x ) называется периодической, если T 0 x D f(x+T)=f(x) • Т называется периодом функции. • Все тригонометрические функции являются периодическими.
Определение 8. Функция f ( x ) называется периодической, если T 0 x D f(x+T)=f(x) • Т называется периодом функции. • Все тригонометрические функции являются периодическими.
 Определение 9. Пусть задана функция у= f ( x ) с областью определения D и множеством значений Е. • Есликаждомузначению у Е соответствуетединственное значение х D , тоопределенафункция х = (у) с областью определения Е имножествомзначений D. • Такаяфункция (у) называется обратной кфункции f ( x ) и записываетсявследующемвиде: x = (у) = f — 1 ( y ). • П ро функции у = f ( x ) и х= (у) говорят, что они являются взаимно обратными. Чтобы найти функцию х= (у), обратную к функции у = f ( x ), достаточно решить уравнение f ( x )= y относительно х (если это возможно).
Определение 9. Пусть задана функция у= f ( x ) с областью определения D и множеством значений Е. • Есликаждомузначению у Е соответствуетединственное значение х D , тоопределенафункция х = (у) с областью определения Е имножествомзначений D. • Такаяфункция (у) называется обратной кфункции f ( x ) и записываетсявследующемвиде: x = (у) = f — 1 ( y ). • П ро функции у = f ( x ) и х= (у) говорят, что они являются взаимно обратными. Чтобы найти функцию х= (у), обратную к функции у = f ( x ), достаточно решить уравнение f ( x )= y относительно х (если это возможно).
 • Примеры • 1)Дляфункции у = 2 х обратной функциейявляетсяфункция х=0, 5 у. • 2)Дляфункции у = х2 , х [0; 1], обратнойфункциейявляется уx
• Примеры • 1)Дляфункции у = 2 х обратной функциейявляетсяфункция х=0, 5 у. • 2)Дляфункции у = х2 , х [0; 1], обратнойфункциейявляется уx

 Из определения обратной функции вытекает , • чтофункция у = f ( x ) имеетобратную тогдаитолькотогда, когдафункция f ( x ) задаетвзаимнооднозначное соответствиемеждумножествами D и Е. • Отсюдаследует, чтолюбая строго монотонная функция имеет обратную. • Приэтомеслифункциявозрастает (убывает), тообратнаяфункциятакже возрастает(убывает).
Из определения обратной функции вытекает , • чтофункция у = f ( x ) имеетобратную тогдаитолькотогда, когдафункция f ( x ) задаетвзаимнооднозначное соответствиемеждумножествами D и Е. • Отсюдаследует, чтолюбая строго монотонная функция имеет обратную. • Приэтомеслифункциявозрастает (убывает), тообратнаяфункциятакже возрастает(убывает).
 Заметим, что функция у = f ( x ) и обратная ей х= (у) изображаются одной и той же кривой, • т. е. графикиихсовпадают. • Еслижеусловиться, что, как обычно, независимуюпеременную (т. е. аргумент)обозначитьчерез х , азависимуюпеременнуючерез у, тофункцияобратнаяфункции у = f ( x ) запишетсяввиде у = ( x ).
Заметим, что функция у = f ( x ) и обратная ей х= (у) изображаются одной и той же кривой, • т. е. графикиихсовпадают. • Еслижеусловиться, что, как обычно, независимуюпеременную (т. е. аргумент)обозначитьчерез х , азависимуюпеременнуючерез у, тофункцияобратнаяфункции у = f ( x ) запишетсяввиде у = ( x ).
 Это означает, что точка M 1 ( x 0 ; y 0 ) кривой у = f ( x ) становится точкой М 2 (у 0 ; х 0 ) кривой у = (х). • Ноточки М 1 и М 2 симметричны относительнопрямой у = х. • Поэтому графики взаимно обратных функций у = f ( x ) и у = (х) симметричны относительно биссектрисы первого и третьего координатных углов.
Это означает, что точка M 1 ( x 0 ; y 0 ) кривой у = f ( x ) становится точкой М 2 (у 0 ; х 0 ) кривой у = (х). • Ноточки М 1 и М 2 симметричны относительнопрямой у = х. • Поэтому графики взаимно обратных функций у = f ( x ) и у = (х) симметричны относительно биссектрисы первого и третьего координатных углов.
 Определение 9. Пусть функция у = f ( u ) определена на множестве D , а функция и = (х) на множестве D 1 , причем для x D 1 соответствующее значение и = ( x ) D. • Тогданамножестве D 1 определенафункция и = f ( ( x )), котораяназывается сложной функцией от х (или суперпозицией заданныхфункций, или функцией от функции) • Переменную и = ( x )называют промежуточным аргументом сложной функции. • Например, функция у = sin 2 x есть суперпозициядвухфункций у = sin u и и = 2 х. • Сложнаяфункцияможетиметьнесколько промежуточныхаргументов.
Определение 9. Пусть функция у = f ( u ) определена на множестве D , а функция и = (х) на множестве D 1 , причем для x D 1 соответствующее значение и = ( x ) D. • Тогданамножестве D 1 определенафункция и = f ( ( x )), котораяназывается сложной функцией от х (или суперпозицией заданныхфункций, или функцией от функции) • Переменную и = ( x )называют промежуточным аргументом сложной функции. • Например, функция у = sin 2 x есть суперпозициядвухфункций у = sin u и и = 2 х. • Сложнаяфункцияможетиметьнесколько промежуточныхаргументов.
 Основныеэлементарные функции
Основныеэлементарные функции
 • Примечание. Функции, построенные из основных элементарных функций и полученные при помощи конечного числа арифметических действий, называются элементарными.
• Примечание. Функции, построенные из основных элементарных функций и полученные при помощи конечного числа арифметических действий, называются элементарными.

