ГИПЕРБОЛОЙ называется множество точек плоскости, абсолютная величина разности






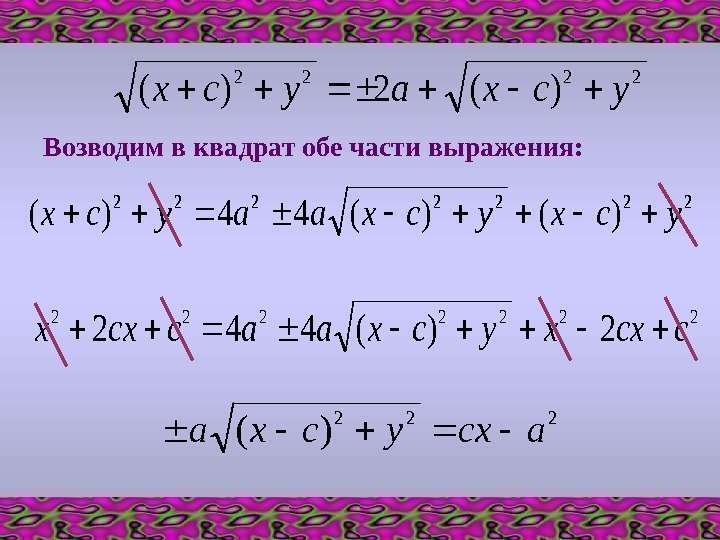




4.4..ppt
- Размер: 290.0 Кб
- Автор:
- Количество слайдов: 12
Описание презентации ГИПЕРБОЛОЙ называется множество точек плоскости, абсолютная величина разности по слайдам
 ГИПЕРБОЛОЙ называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (меньшая, чем расстояние между фокусами)
ГИПЕРБОЛОЙ называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (меньшая, чем расстояние между фокусами)
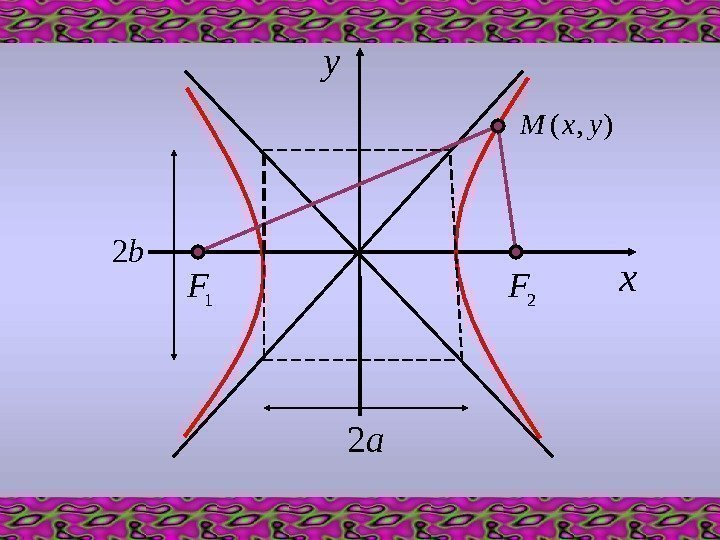
 xy 2 F 1 F ), (yx. M a 2 b
xy 2 F 1 F ), (yx. M a 2 b
 Введем обозначения: a – действительная полуось гиперболы b – мнимая полуось гиперболы Для любой точки М(х, у), принадлежащей гиперболе, по определению выполняется равенство: )0; (21 c. FF 2 21 a. MFM
Введем обозначения: a – действительная полуось гиперболы b – мнимая полуось гиперболы Для любой точки М(х, у), принадлежащей гиперболе, по определению выполняется равенство: )0; (21 c. FF 2 21 a. MFM
 Прямые, проходящие через начало координат и имеющие угловые коэффициенты и называются асимптотами гиперболы. a b Асимптоты делят плоскость на 4 области, в двух из которых расположена гипербола. Точки гиперболы по мере удавления от оси у приближаются к асимптотам, т. е. расстояние между точками гиперболы и асимптотой при увеличении х уменьшается и стремится к нулю.
Прямые, проходящие через начало координат и имеющие угловые коэффициенты и называются асимптотами гиперболы. a b Асимптоты делят плоскость на 4 области, в двух из которых расположена гипербола. Точки гиперболы по мере удавления от оси у приближаются к асимптотам, т. е. расстояние между точками гиперболы и асимптотой при увеличении х уменьшается и стремится к нулю.
 ТЕОРЕМА Для того, чтобы точка М(х, у) принадлежала гиперболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению1 2 2 22 b y a x где 222 acb
ТЕОРЕМА Для того, чтобы точка М(х, у) принадлежала гиперболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению1 2 2 22 b y a x где 222 acb
 Покажем, что координаты точки, принадлежащей гиперболе, удовлетворяют уравнению (2). Т. к. точка М(х, у) принадлежит гиперболе, то по определению гиперболы, должно выполнятся условие Выразим каждое расстояние по формуле расстояния между двумя точками: a. MFMF 221 )0; ( 1 c. F ); (yx. M 22 1 )(ycx. M
Покажем, что координаты точки, принадлежащей гиперболе, удовлетворяют уравнению (2). Т. к. точка М(х, у) принадлежит гиперболе, то по определению гиперболы, должно выполнятся условие Выразим каждое расстояние по формуле расстояния между двумя точками: a. MFMF 221 )0; ( 1 c. F ); (yx. M 22 1 )(ycx. M
 Тогда: )0; ( 2 c. F); (yx. M 22 2)(ycx. MF aycxycx. MFMF 2)()( 2222 21 aycxycx 2)()(
Тогда: )0; ( 2 c. F); (yx. M 22 2)(ycx. MF aycxycx. MFMF 2)()( 2222 21 aycxycx 2)()(
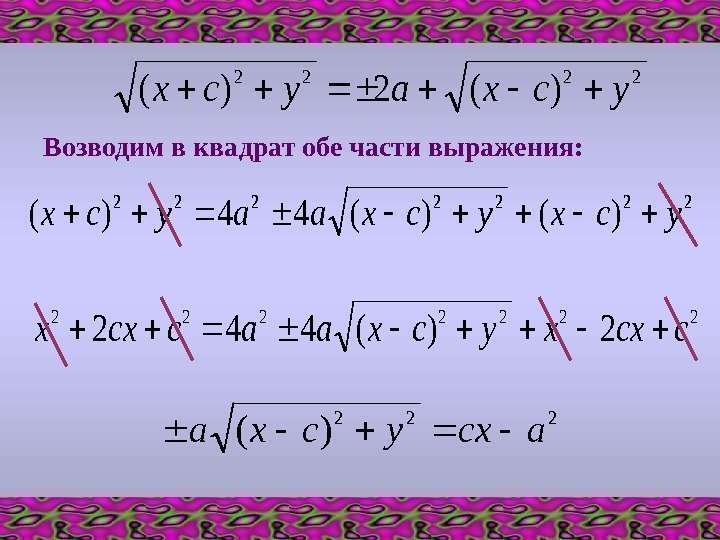 2222 )(2)(ycxaycx 2222222 )()(44)(ycxycxaaycx. Возводим в квадрат обе части выражения: 2222222 2)(442 ccxxycxaaccxx 222 )(acxycxa
2222 )(2)(ycxaycx 2222222 )()(44)(ycxycxaaycx. Возводим в квадрат обе части выражения: 2222222 2)(442 ccxxycxaaccxx 222 )(acxycxa
 Возводим в еще раз квадрат: 222224 22 yacaxcaxaxccxaa 42222 acayaxaxc )()( 2222 acayaacx 2 b 2 b Делим все выражение на 22 ba
Возводим в еще раз квадрат: 222224 22 yacaxcaxaxccxaa 42222 acayaxaxc )()( 2222 acayaacx 2 b 2 b Делим все выражение на 22 ba
 1 2 2 22 b y a x
1 2 2 22 b y a x
 Отношение фокусного расстояния к длине действительной оси гиперболы называется ЭКСЦЕНТРИСИТЕТОМ a c
Отношение фокусного расстояния к длине действительной оси гиперболы называется ЭКСЦЕНТРИСИТЕТОМ a c
 Для гиперболы Следовательно, для гиперболы Чем меньше отношение мнимой и действительной полуосей, тем меньше эксцентриситет и тем более гипербола будет прижата к оси х , и наоборот. ac 2 22 2 1 a ba a c
Для гиперболы Следовательно, для гиперболы Чем меньше отношение мнимой и действительной полуосей, тем меньше эксцентриситет и тем более гипербола будет прижата к оси х , и наоборот. ac 2 22 2 1 a ba a c
