Функция f(x) называется бесконечно малой величиной ,

Функция f(x) называется бесконечно малой величиной , если при или при 0 xx x ее предел равен нулю: 0)(lim 0 xf xx или 0)(lim xf x

Функция xycos является бесконечно малой величиной при 2 x поскольку 0 coslim 2 x x

Если функция f(x) имеет при 0 xx или приx предел, равный А, то ее можно представить в виде суммы этого числа А и бесконечно малой величины )(x при 0 xx илиx )()()(lim 0 x. Axf x xx

Проведем доказательство для случая По условию , следовательно 0 xx Axf xx )(lim 0 Axf )(для любого, сколь угодно малого числа ε >0 , найдется такое положительное число δ , что при всех х , таких что | x — x 0 |< δ , выполняется неравенство:

Обозначим: Тогда , а это означает, что 0)(lim 0 x xx )()( x. Axf )( x Следовательно, по определению, )(x является бесконечно малой величиной при 0 xx

Верна и обратная Если функцию f(x) можно представить как сумму числа А и бесконечно малой величины 0 xx или приx )(xпри 0 xx илиx Axfx. Axf x xx )(lim)()( 0 то число А является пределом этой функции при

1 Алгебраическая сумма бесконечно малых величин есть величина бесконечно малая.

2 Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая. 3 Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Пусть )1 lg()(105)(xxxx являются бесконечно малыми величинами при 2 x поскольку 0)1 lg(lim 0)105(lim 22 xx xx Функция xxfsin)(

является ограниченной на любом промежутке, поскольку 1 sinx Функция 5)( 2 xx имеет предел при 1)5(lim 2 2 x x 2 x Тогда функции )1 lg(105)()(xxxx

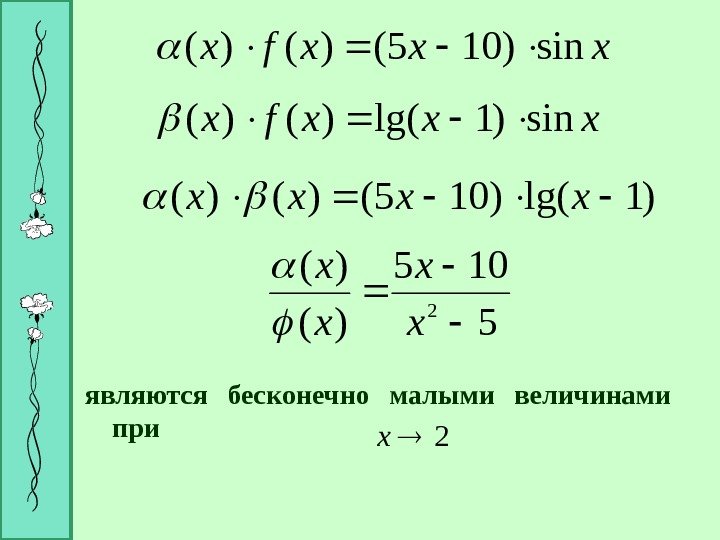xxxfxsin)105()()( )1 lg()105()()(xxxx 5 105 )( )( 2 x x являются бесконечно малыми величинами при 2 x xxxfxsin)1 lg()()(

Предел отношения двух бесконечно малых величин )( )( lim 0 x x x xx может быть равен нулю, тогда α (х) называется бесконечно малой более высокого порядка, чем β (х); может быть равен числу А, не равному нулю, тогда α (х) и β (х) имеют одинаковый порядок малости; может быть равен бесконечности, тогда α (х) называется бесконечно малой более низкого порядка, чем β (х).