Физика. Математика. Лекция 2 Лектор: Загитов Г. Н.








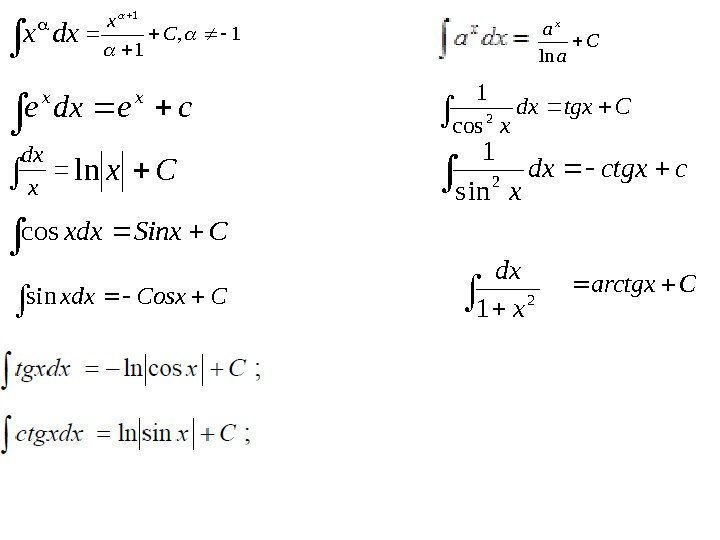





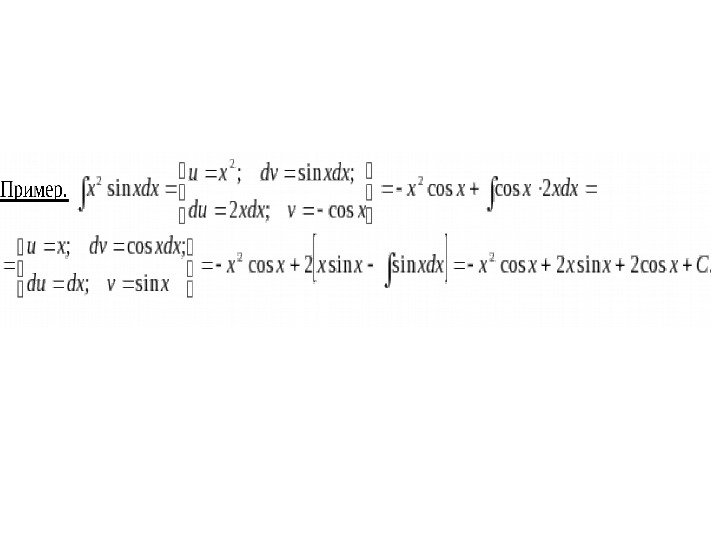
![Определенный интеграл • Пусть на отрезке [ab] задана непрерывная функция y=f(x) Определенный интеграл • Пусть на отрезке [ab] задана непрерывная функция y=f(x)](http://present5.com/presentforday2/20161227/lek_2_lech_images/lek_2_lech_15.jpg)

![Свойства определенного интеграла. 4. Если f(x) ( x) на отрезке [a, b] a Свойства определенного интеграла. 4. Если f(x) ( x) на отрезке [a, b] a](http://present5.com/presentforday2/20161227/lek_2_lech_images/lek_2_lech_17.jpg)






lek_2_lech.pptx
- Размер: 989.5 Кб
- Автор:
- Количество слайдов: 25
Описание презентации Физика. Математика. Лекция 2 Лектор: Загитов Г. Н. по слайдам
 Физика. Математика. Лекция 2 Лектор: Загитов Г. Н.
Физика. Математика. Лекция 2 Лектор: Загитов Г. Н.
 Применение дифференциала для приближенных вычислений. Из определения производной функции: Можно записать: , или . Величина — бесконечно малая более высокого порядка, чем f’(x)Δx, т. е. f'(x)Δx- главная часть приращения у. Отбрасывая вторую часть в этой формуле, можем написать: Δy=f’(x)Δx или f(x+Δx)-f(x)=f’(x)Δx; отсюда можем вычислить значение функции в точке x+Δx: f(x+Δx)=f(x)+f ’(x)Δx ; если f(х) и f’(x) можно легко вычислить в точке x. αΔx
Применение дифференциала для приближенных вычислений. Из определения производной функции: Можно записать: , или . Величина — бесконечно малая более высокого порядка, чем f’(x)Δx, т. е. f'(x)Δx- главная часть приращения у. Отбрасывая вторую часть в этой формуле, можем написать: Δy=f’(x)Δx или f(x+Δx)-f(x)=f’(x)Δx; отсюда можем вычислить значение функции в точке x+Δx: f(x+Δx)=f(x)+f ’(x)Δx ; если f(х) и f’(x) можно легко вычислить в точке x. αΔx
 Пример : вычислить без таблицы Sin 29 • Sin 29 =Sin(30 -1 ), поэтому примем x=30 , а Δx=-1 . • Sin 29 =Sin 30 +Cos 30 (-0, 017)=0, 485. • 1 =3, 14/180=0, 017 • Sin’x=Cosx • Вычислите без таблицы lg 101.
Пример : вычислить без таблицы Sin 29 • Sin 29 =Sin(30 -1 ), поэтому примем x=30 , а Δx=-1 . • Sin 29 =Sin 30 +Cos 30 (-0, 017)=0, 485. • 1 =3, 14/180=0, 017 • Sin’x=Cosx • Вычислите без таблицы lg 101.
 Частные производные функций Допустим дана функция от двух переменных z=f(x, y). Считая у постоянной величиной найдем частное производное по x: ==; и считая x постоянной-частное производное по y: = •
Частные производные функций Допустим дана функция от двух переменных z=f(x, y). Считая у постоянной величиной найдем частное производное по x: ==; и считая x постоянной-частное производное по y: = •
 Частные и полный дифференциал функции Находим частные дифференциалы функции по переменным x и y: =; =dy=dy. Сумма частных дифференциалов называется полным дифференциалом. dz(x, y)=+=+dy. •
Частные и полный дифференциал функции Находим частные дифференциалы функции по переменным x и y: =; =dy=dy. Сумма частных дифференциалов называется полным дифференциалом. dz(x, y)=+=+dy. •
 Задача : найдите абсолютную погрешность в определении объема цилиндра, если при измерениях были получены радиуса r= (6± 0, 1) см и высоты h=(10± 0, 2) cм. Решение: Объем цилиндра: V=h. Принимая за погрешность дифференциал функции получаем: ΔV=d. V=dr+=2πrhΔr+Δh= r(2 h Δr+r Δh)= 3, 14× 6(2× 10× 0, 1+6× 0, 2)=603. •
Задача : найдите абсолютную погрешность в определении объема цилиндра, если при измерениях были получены радиуса r= (6± 0, 1) см и высоты h=(10± 0, 2) cм. Решение: Объем цилиндра: V=h. Принимая за погрешность дифференциал функции получаем: ΔV=d. V=dr+=2πrhΔr+Δh= r(2 h Δr+r Δh)= 3, 14× 6(2× 10× 0, 1+6× 0, 2)=603. •
 Интегральное исчисление. Первообразная функция. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство: F (x) = f(x). Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
Интегральное исчисление. Первообразная функция. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство: F (x) = f(x). Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
 Неопределенный интеграл. Определение : Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C. Записывают : ; )()(Cx. Fdxxf
Неопределенный интеграл. Определение : Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C. Записывают : ; )()(Cx. Fdxxf
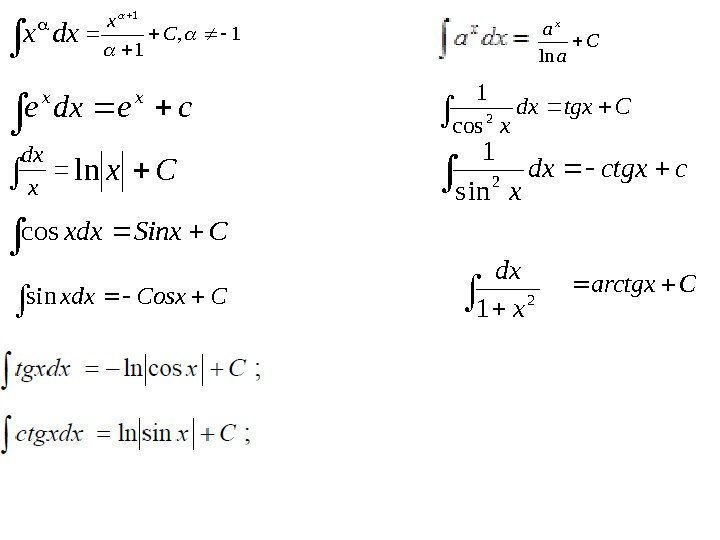 dxx 1, 1 1 C x cedxe xx x dx Cxln CSinxxdxcos CCosxxdxsin C a ax ln Ctgxdx x 2 cos 1 cctgxdx x 2 sin 1 2 1 x dx Carctgx
dxx 1, 1 1 C x cedxe xx x dx Cxln CSinxxdxcos CCosxxdxsin C a ax ln Ctgxdx x 2 cos 1 cctgxdx x 2 sin 1 2 1 x dx Carctgx
 Свойства: где u, v, w – некоторые функции от х. Пример: ); ())(()(. 1 xf. Cx. Fdxxf ; )()(. 2 dxxfd ; )()(. 3 Cx. Fxd. F ; )(. 4 wdxvdxudxdxwvu ; )()(. 5 dxxf. C ; cos 2 3 1 sin 2)1 sin 2( 322 Cxxxdxxdxxx
Свойства: где u, v, w – некоторые функции от х. Пример: ); ())(()(. 1 xf. Cx. Fdxxf ; )()(. 2 dxxfd ; )()(. 3 Cx. Fxd. F ; )(. 4 wdxvdxudxdxwvu ; )()(. 5 dxxf. C ; cos 2 3 1 sin 2)1 sin 2( 322 Cxxxdxxdxxx
 Методы интегрирования А) Непосредственное интегрирование.
Методы интегрирования А) Непосредственное интегрирование.
 Б) Способ подстановки (замены переменных).
Б) Способ подстановки (замены переменных).
 В) Интегрирование по частям.
В) Интегрирование по частям.
 Пример. Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства. dxexxe xvxdxdv dxedueu xdxe xx xx x 22 22 2 2 sinsin sin; cos ; 2; cos dxxexe xedxexxexe xvxdxdv dxedueu xx xx 22 22 cos 4 cos 2 sin 2 coscos 2 sin ; cos; sin ; 2; . )cos 2(sin 5 cos 2 2 Cxx e xdxe x x
Пример. Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства. dxexxe xvxdxdv dxedueu xdxe xx xx x 22 22 2 2 sinsin sin; cos ; 2; cos dxxexe xedxexxexe xvxdxdv dxedueu xx xx 22 22 cos 4 cos 2 sin 2 coscos 2 sin ; cos; sin ; 2; . )cos 2(sin 5 cos 2 2 Cxx e xdxe x x
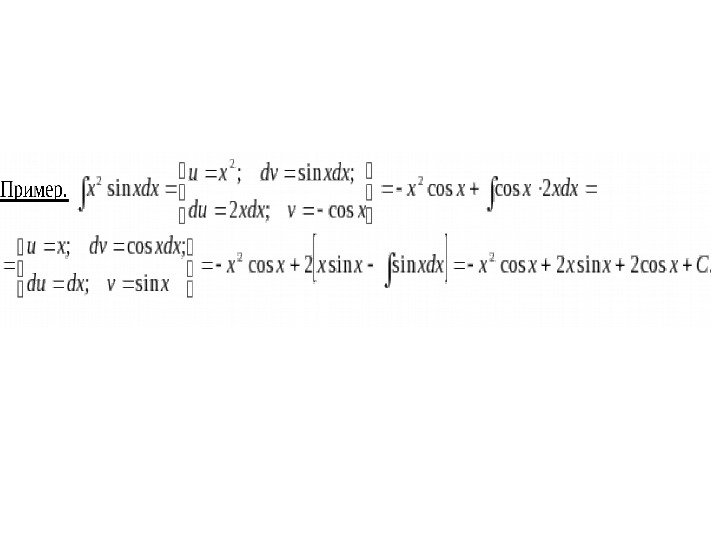
![Определенный интеграл • Пусть на отрезке [ab] задана непрерывная функция y=f(x) Определенный интеграл • Пусть на отрезке [ab] задана непрерывная функция y=f(x)](http://present5.com/presentforday2/20161227/lek_2_lech_images/lek_2_lech_15.jpg) Определенный интеграл • Пусть на отрезке [ab] задана непрерывная функция y=f(x)
Определенный интеграл • Пусть на отрезке [ab] задана непрерывная функция y=f(x)
 Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b]. S n = f( 1 ) x 1 + f( 2 ) x 2 + … + f( n ) x n = Внутри каждого отрезка выберем некоторую точку . x 0 < 1 < x 1 , x 1 < 2 < x 2 , … , x n-1 < n < x n. Определение: Если при любых разбиениях отрезка [a, b] таких, что max x i 0 и произвольном выборе точек i интегральная сумма стремится к пределу S, который называется опреде- ленным интегралом от f(x) на отрезке [a, b]: n i iixf 1 )( n i iinxf. S 1 )(
Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b]. S n = f( 1 ) x 1 + f( 2 ) x 2 + … + f( n ) x n = Внутри каждого отрезка выберем некоторую точку . x 0 < 1 < x 1 , x 1 < 2 < x 2 , … , x n-1 < n < x n. Определение: Если при любых разбиениях отрезка [a, b] таких, что max x i 0 и произвольном выборе точек i интегральная сумма стремится к пределу S, который называется опреде- ленным интегралом от f(x) на отрезке [a, b]: n i iixf 1 )( n i iinxf. S 1 )(
![Свойства определенного интеграла. 4. Если f(x) ( x) на отрезке [a, b] a Свойства определенного интеграла. 4. Если f(x) ( x) на отрезке [a, b] a](http://present5.com/presentforday2/20161227/lek_2_lech_images/lek_2_lech_17.jpg) Свойства определенного интеграла. 4. Если f(x) ( x) на отрезке [a, b] a < b, то; )()(. 1 b a dxxf. Adxx. Af b a b a dxxfdxxfxf)()())()((. 32121 0)(. 2 a a dxxf b a dxxdxxf)()(
Свойства определенного интеграла. 4. Если f(x) ( x) на отрезке [a, b] a < b, то; )()(. 1 b a dxxf. Adxx. Af b a b a dxxfdxxfxf)()())()((. 32121 0)(. 2 a a dxxf b a dxxdxxf)()(
 5. Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то: 6. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка такая, что b a ab. Mdxxfabm)()()( b a a b dxxf)()(.
5. Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то: 6. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка такая, что b a ab. Mdxxfabm)()()( b a a b dxxf)()(.
 8. Для произвольных чисел a, b, c справедливо равенство : Теорема: ( Теорема Ньютона – Лейбница) Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то b ab a a. Fb. Fdxxf F(x) =)()()(
8. Для произвольных чисел a, b, c справедливо равенство : Теорема: ( Теорема Ньютона – Лейбница) Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то b ab a a. Fb. Fdxxf F(x) =)()()(
 Пример. . 4 sin 4 1 4 2 sin 2 1 )2 cos 1( 2 1 coscossin 1 2/; 0 ; sin 1 2/ 0 2 1 0 2 tt dtttdttdtt tx dxx
Пример. . 4 sin 4 1 4 2 sin 2 1 )2 cos 1( 2 1 coscossin 1 2/; 0 ; sin 1 2/ 0 2 1 0 2 tt dtttdttdtt tx dxx
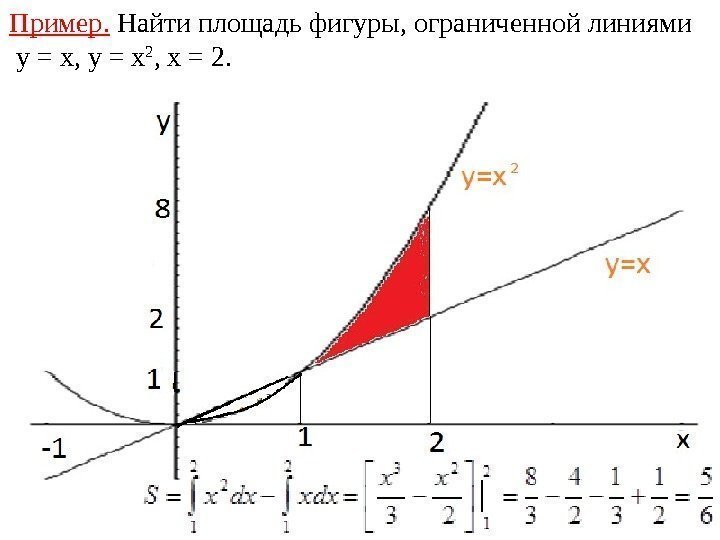
 Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x 2 , x = 2.
Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x 2 , x = 2.
 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную (аргумент) х , искомую функцию y = f ( x ) и ее производные различных порядков y ′ , y ′′ , . . , : F ( x , y ′′ , …, )= 0. Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение. Например, дифференциальные уравнения
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную (аргумент) х , искомую функцию y = f ( x ) и ее производные различных порядков y ′ , y ′′ , . . , : F ( x , y ′′ , …, )= 0. Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение. Например, дифференциальные уравнения
 Решением дифференциального уравнения называется такая функция y = y ( x ) , которая при подстановке в это уравнение обращает его в тождество. Например, функция y = + Cx , где С – любая постоянная величина, является решением дифференциального уравнения y ′ x −− y = 0. Заметим, что данное дифференциальное равнение имеет бесконечное множество решений, так как С – произвольная постоянная величина. Процесс нахождения решения называется интегрированием дифференциального уравнения.
Решением дифференциального уравнения называется такая функция y = y ( x ) , которая при подстановке в это уравнение обращает его в тождество. Например, функция y = + Cx , где С – любая постоянная величина, является решением дифференциального уравнения y ′ x −− y = 0. Заметим, что данное дифференциальное равнение имеет бесконечное множество решений, так как С – произвольная постоянная величина. Процесс нахождения решения называется интегрированием дифференциального уравнения.
 Общим решением дифференциального уравнения n -го порядка называется функция y=f (x, , , . . , ) , зависящая от х и n произвольных независимых постоянных, обращающая это уравнение в тождество при любых значениях постоянных , , . Частным решением дифференциального уравнения n -ого порядка называется решениеy=f (x, ), где — фиксированные числа, которое получается из общего, если придать определенные значения произвольным постоянным , , .
Общим решением дифференциального уравнения n -го порядка называется функция y=f (x, , , . . , ) , зависящая от х и n произвольных независимых постоянных, обращающая это уравнение в тождество при любых значениях постоянных , , . Частным решением дифференциального уравнения n -ого порядка называется решениеy=f (x, ), где — фиксированные числа, которое получается из общего, если придать определенные значения произвольным постоянным , , .
