Если каждому натуральному числу n по некоторому закону

Если каждому натуральному числу n по некоторому закону поставлено в соответствие определенное число a n , то говорят, что задана числовая последовательность nnaaaa. . . ,

Числа a 1 , a 2 …a n называются членами последовательности, а число a n называется общим членом или n -ым членом данной последовательности. Например: . . . 2. . . 8, 6, 4, 2 n 1 2. . . 1. . . 4 1 , 3 1 , 2 1 , 1 n

Изобразим члены последовательности (2) точками на числовой оси. 01 2 1 31 4 1 51 Можно заметить, что члены последовательности с ростом n сколь угодно близко приближаются к нулю.

Последовательность { a n } называется ограниченной сверху (снизу), если существует такое число М ( m ), что любой элемент этой последовательности удовлетворяет неравенству: ma Ma n n

Последовательность { a n } называется ограниченной, если она ограничена сверху и снизу: Mam n

Последовательность (1) ограничена снизу, но не сверху. Последовательность (2) ограничена, т. к. все ее элементы находятся внутри промежутка [0, 1]. Если выполняется условие 1 nnaa то последовательность называется возрастающей. Если выполняется условие 1 nn aa то последовательность называется убывающей. Последовательность (1) возрастающая. Последовательность (2) убывающая.

Число А называется пределом числовой последовательности { a n } , если для любого, сколь угодно малого числа ε >0 , найдется такой номер N , что при всех n>N , выполняется неравенство: Aa n n lim

Последовательность, имеющая предел, называется сходящейся. В противном случае последовательность расходящаяся. Смысл определения предела числовой последовательности: Для достаточно больших номеров n члены последовательности очень мало отличаются от числа А (меньше, чем на число , ε , каким бы малым оно не было).

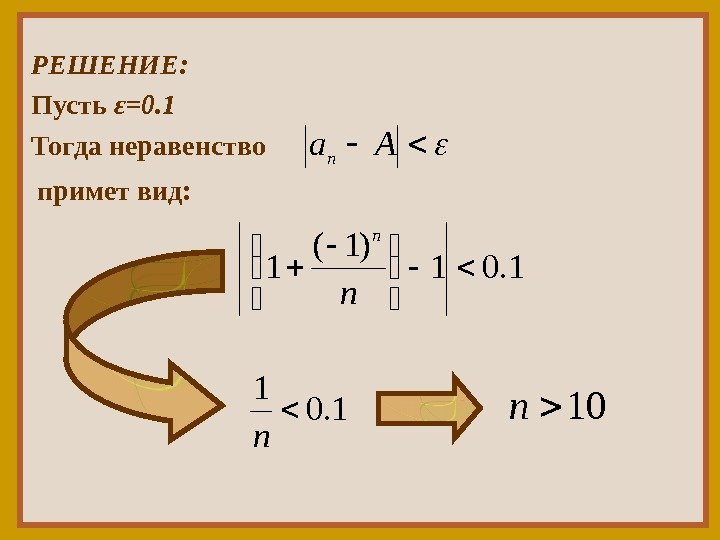
ПРИМЕР. Дана последовательность. . . )1( 1. . . , 5 4 , 4 5 , 3 2 , 2 3 , 0 n n Показать, что предел этой последовательности равен 1.

РЕШЕНИЕ: Пусть ε =0. 1 Тогда неравенство Aa n примет вид: 1. 01)1( 1 n n 1. 0 1 n 10 n

Если ε =0. 0 1 , то неравенство выполняется при 100 n Для любого ε >0 , неравенство выполняется при 1 n Т. е. для любого ε >0 существует номер 1 n Что для всех n>N , выполняется неравенство: 1 na 1 lim n n a

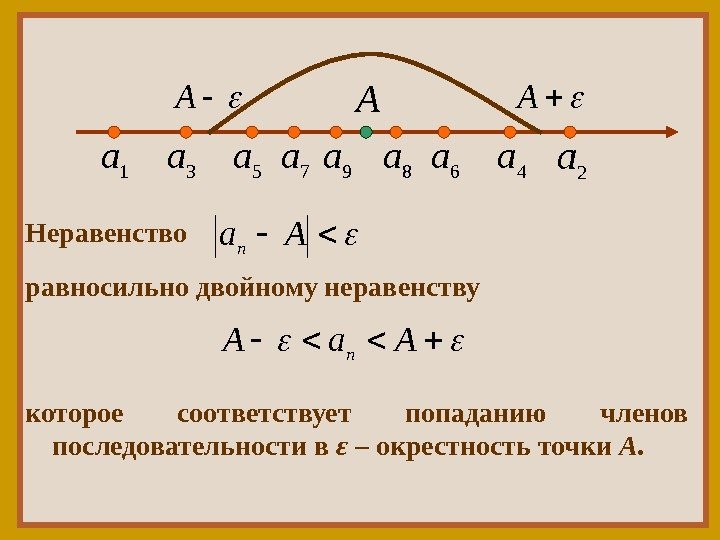
Рассмотрим геометрический смысл предела числовой последовательности. Для этого изобразим члены последовательности (3) точками на числовой оси. . , 9 8 , 8 9 , 7 6 , 6 7 5 4 , 4 5 , 3 2 , 2 3 , 0 9876 54321 aaaaa

1 a 2 a. Неравенство 3 a 4 a 5 a 6 a 7 a 8 a 9 a A Aa n равносильно двойному неравенству Aa. An которое соответствует попаданию членов последовательности в ε – окрестность точки А.

Т. е. число А есть предел числовой последовательности { a n } , если для любого, сколь угодно малого числа ε >0 , найдется такой номер N , начиная с которого все члены последовательности будут заключены в ε – окрестности точки А, какой бы узкой она не была. Вне этой окрестности может быть только конечное число членов последовательности.