Если каждому элементу х множества Х ставится в










![Функции, возрастающие и убывающие называются монотонными. Например: 2 xy Возрастает на промежутке: ]0; Функции, возрастающие и убывающие называются монотонными. Например: 2 xy Возрастает на промежутке: ]0;](http://present5.com/presentforday2/20170128/5.3._images/5.3._12.jpg)








5.3..ppt
- Размер: 445.5 Кб
- Автор:
- Количество слайдов: 22
Описание презентации Если каждому элементу х множества Х ставится в по слайдам
 Если каждому элементу х множества Х ставится в соответствие определенный элемент у множества У, то говорят, что на множестве Х задана функция )(xfy
Если каждому элементу х множества Х ставится в соответствие определенный элемент у множества У, то говорят, что на множестве Х задана функция )(xfy
 х называется независимой переменной у называется зависимой переменной Х – область определения функции У – область значений функции Совокупность точек плоскости ХОУ, удовлетворяющих уравнению)(xfy называется графиком этой функции.
х называется независимой переменной у называется зависимой переменной Х – область определения функции У – область значений функции Совокупность точек плоскости ХОУ, удовлетворяющих уравнению)(xfy называется графиком этой функции.
 1. Аналитический Функция задана формулой вида)(xfy Например: 1 3 xy Область определения: x Область значений: y
1. Аналитический Функция задана формулой вида)(xfy Например: 1 3 xy Область определения: x Область значений: y
 22 1 xy Область определения: 11 x Область значений: 10 y 3 0, 1 0, 3 xx xx y
22 1 xy Область определения: 11 x Область значений: 10 y 3 0, 1 0, 3 xx xx y
 2. Табличный Функция задана таблицей, в которой содержатся значения аргумента х и соответствующие значения функции f(x). Например: таблицы логарифмов. 3. Графический Функция задана в виде графика y=f(x).
2. Табличный Функция задана таблицей, в которой содержатся значения аргумента х и соответствующие значения функции f(x). Например: таблицы логарифмов. 3. Графический Функция задана в виде графика y=f(x).
 Функция y=f(x) называется четной , если для любого х 1. Четность)()(xfxf
Функция y=f(x) называется четной , если для любого х 1. Четность)()(xfxf
 Функция y=f(x) называется нечетной , если для любого х )()( xfxf Если оба эти условия не выполняются, то функция называется функцией общего вида.
Функция y=f(x) называется нечетной , если для любого х )()( xfxf Если оба эти условия не выполняются, то функция называется функцией общего вида.
 Например: 13 xy — нечетная, т. к. 33 )( xx 2 2 xy — четная, т. к. 3 32 xxy 22 )(xx — общего вида . График четной функции симметричен относительно оси ординат. График нечетной функции симметричен относительно начала координат.
Например: 13 xy — нечетная, т. к. 33 )( xx 2 2 xy — четная, т. к. 3 32 xxy 22 )(xx — общего вида . График четной функции симметричен относительно оси ординат. График нечетной функции симметричен относительно начала координат.
 Функция y=f(x) называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. 2. Монотонность
Функция y=f(x) называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. 2. Монотонность
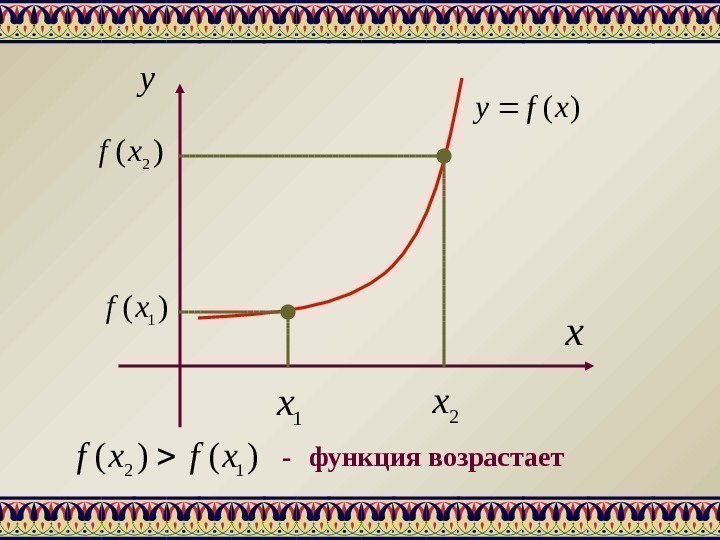
 — функция возрастает — функция убывает 1221, xx. Xxx )()(12 xfxf
— функция возрастает — функция убывает 1221, xx. Xxx )()(12 xfxf
 xy )(xfy 1 x 2 x)( 1 xf )(2 xf )()(12 xfxf — функция возрастает
xy )(xfy 1 x 2 x)( 1 xf )(2 xf )()(12 xfxf — функция возрастает
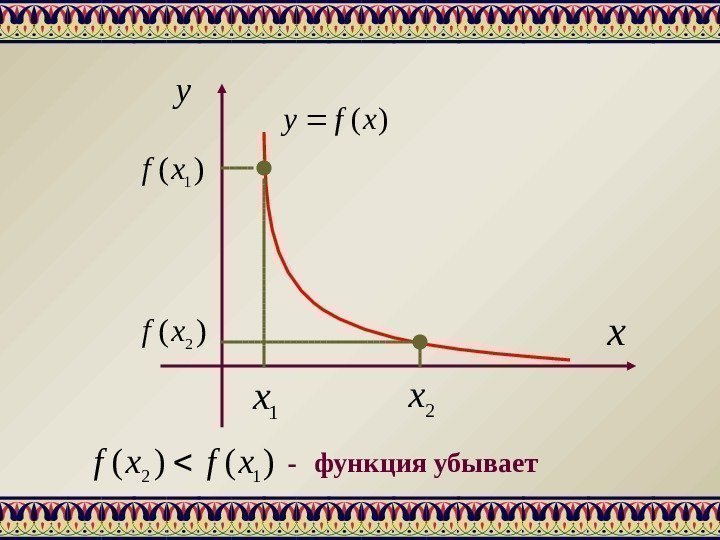
 xy )(xfy 1 x 2 x)( 1 xf )(2 xf )()(12 xfxf — функция убывает
xy )(xfy 1 x 2 x)( 1 xf )(2 xf )()(12 xfxf — функция убывает
![Функции, возрастающие и убывающие называются монотонными. Например: 2 xy Возрастает на промежутке: ]0; Функции, возрастающие и убывающие называются монотонными. Например: 2 xy Возрастает на промежутке: ]0;](http://present5.com/presentforday2/20170128/5.3._images/5.3._12.jpg) Функции, возрастающие и убывающие называются монотонными. Например: 2 xy Возрастает на промежутке: ]0; ( Убывает на промежутке: ); 0[
Функции, возрастающие и убывающие называются монотонными. Например: 2 xy Возрастает на промежутке: ]0; ( Убывает на промежутке: ); 0[
 Функция y=f(x) называется ограниченной на промежутке Х, если существует число М > 0, такое, что для любого х выполняется неравенство: 3. Ограниченность. Mxf)(
Функция y=f(x) называется ограниченной на промежутке Х, если существует число М > 0, такое, что для любого х выполняется неравенство: 3. Ограниченность. Mxf)(
 В противном случае функция называется неограниченной. Например: xy cos — ограничена на всей числовой оси, т. к. для любого х1 cosx
В противном случае функция называется неограниченной. Например: xy cos — ограничена на всей числовой оси, т. к. для любого х1 cosx
 Функция y=f(x) называется периодичной с периодом Т, не равным нулю, если для любого х выполняется равенство: 4. Периодичность)()(xf. Txf
Функция y=f(x) называется периодичной с периодом Т, не равным нулю, если для любого х выполняется равенство: 4. Периодичность)()(xf. Txf
 Например: xy cos -периодичная с периодом, равным 2 П , т. к. для любого х xx cos)2 cos(
Например: xy cos -периодичная с периодом, равным 2 П , т. к. для любого х xx cos)2 cos(
 Введем понятие обратной функции. Пусть задана функция от аргумента х : y=f(x) , определенная на множестве Х с областью значений У. Yy Поставим в соответствие каждому значению Xx единственное значение при котором f(x) =y.
Введем понятие обратной функции. Пусть задана функция от аргумента х : y=f(x) , определенная на множестве Х с областью значений У. Yy Поставим в соответствие каждому значению Xx единственное значение при котором f(x) =y.
 Функция x=φ(y) определенная на множестве У с областью значений Х, называется обратной к функции y=f(x) . Традиционно функцию обозначают у а аргумент – х. Поэтому обратную функцию обозначают)()( 1 xfxy
Функция x=φ(y) определенная на множестве У с областью значений Х, называется обратной к функции y=f(x) . Традиционно функцию обозначают у а аргумент – х. Поэтому обратную функцию обозначают)()( 1 xfxy
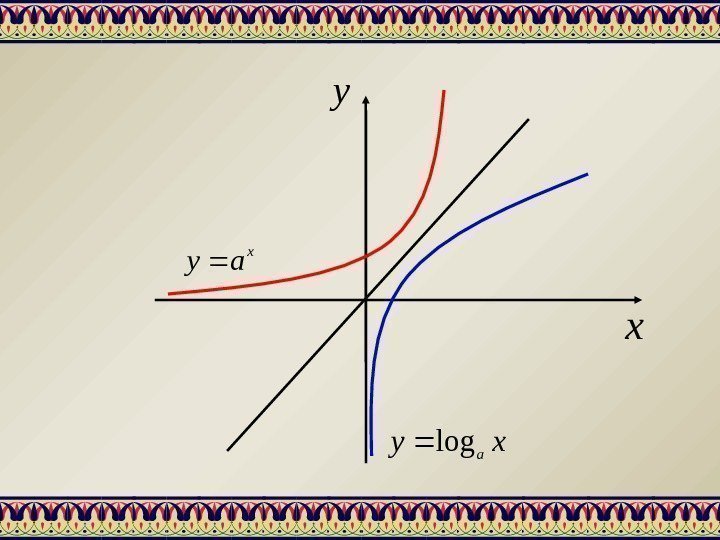
 Например: Для функцииx ay обратной будет функция xy alog Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
Например: Для функцииx ay обратной будет функция xy alog Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
 xy xay xyalog
xy xay xyalog
 Введем понятие сложной функции. Пусть задана функция от аргумента u : y=f(u) , определенная на множестве U с областью значений У. Пусть u в свою очередь, является функцией от переменной х: u=φ(x) , определенной на множестве Х с областью значений U. Функция y=f [φ(x)] определенная на множестве Х с областью значений Y , называется сложной функцией.
Введем понятие сложной функции. Пусть задана функция от аргумента u : y=f(u) , определенная на множестве U с областью значений У. Пусть u в свою очередь, является функцией от переменной х: u=φ(x) , определенной на множестве Х с областью значений U. Функция y=f [φ(x)] определенная на множестве Х с областью значений Y , называется сложной функцией.
