Если дифференцируемая на промежутке Х функция y=f(x) достигает




![Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b]. Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b].](http://present5.com/presentforday2/20170128/8.9._images/8.9._4.jpg)


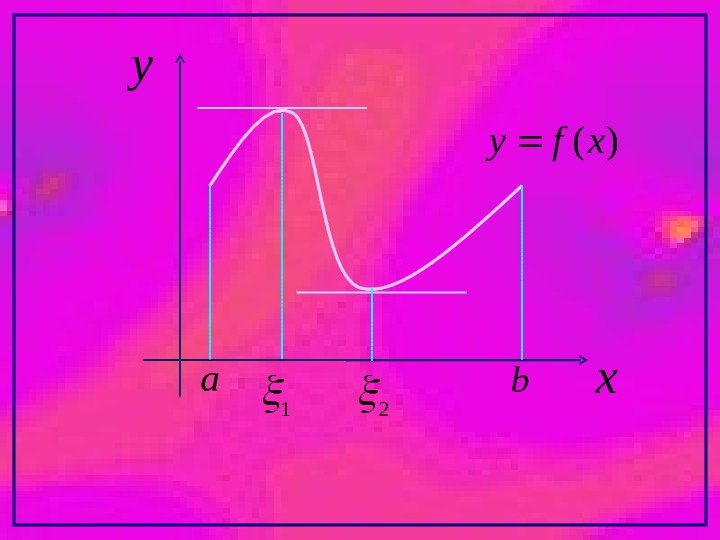

![Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b]. Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b].](http://present5.com/presentforday2/20170128/8.9._images/8.9._11.jpg)







![Возьмем на промежутке Х [a, х ] , тогда по теореме Лагранжа)()(afxfaxf Возьмем на промежутке Х [a, х ] , тогда по теореме Лагранжа)()(afxfaxf](http://present5.com/presentforday2/20170128/8.9._images/8.9._20.jpg)
8.9..ppt
- Размер: 443.5 Кб
- Автор:
- Количество слайдов: 21
Описание презентации Если дифференцируемая на промежутке Х функция y=f(x) достигает по слайдам
 Если дифференцируемая на промежутке Х функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке х 0 этого промежутка, то производная функции в этой точке равна 0: 0)( 0 xf
Если дифференцируемая на промежутке Х функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке х 0 этого промежутка, то производная функции в этой точке равна 0: 0)( 0 xf
 Пусть функция y=f(x) дифференцируема на промежутке Х и в точке Xx 0 принимает наименьшее значение. Тогда )()(00 xfxxf если Xxx 0 Величина 0)()(00 xfxxfy Следовательно 0 x y при 0 x
Пусть функция y=f(x) дифференцируема на промежутке Х и в точке Xx 0 принимает наименьшее значение. Тогда )()(00 xfxxf если Xxx 0 Величина 0)()(00 xfxxfy Следовательно 0 x y при 0 x
 0 lim 0 x y xи 0 lim 0 x y x По условию функция y=f(x) дифференцируема в точке х 0 , следовательно ее предел при 0 x. Переходим в этих неравенствах соответственно к пределу справа и слева: не должен зависеть от способа стремления Δ х к нулю, т. е. 0 limlim 00 x y xx 0)( 0 xf
0 lim 0 x y xи 0 lim 0 x y x По условию функция y=f(x) дифференцируема в точке х 0 , следовательно ее предел при 0 x. Переходим в этих неравенствах соответственно к пределу справа и слева: не должен зависеть от способа стремления Δ х к нулю, т. е. 0 limlim 00 x y xx 0)( 0 xf
 В точке наибольшего или наименьшего значения, достигаемого внутри промежутка Х, касательная к графику функции параллельна оси Х.
В точке наибольшего или наименьшего значения, достигаемого внутри промежутка Х, касательная к графику функции параллельна оси Х.
![Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b]. Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b].](http://present5.com/presentforday2/20170128/8.9._images/8.9._4.jpg) Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b]. 2. Дифференцируема на интервале (a, b). 3. На концах отрезка принимает равные значения: f(a)=f(b). Тогда внутри отрезка существует по крайней мере одна такая точка ξ , в которой производная равна нулю: 0)(f
Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b]. 2. Дифференцируема на интервале (a, b). 3. На концах отрезка принимает равные значения: f(a)=f(b). Тогда внутри отрезка существует по крайней мере одна такая точка ξ , в которой производная равна нулю: 0)(f
 По теореме Вейерштрасса, функция, непрерывная на отрезке, достигает на нем своего наибольшего М и наименьшего m значений. Если оба этих значения достигаются на концах отрезка, то они по условию равны: М= m , а это значит, что функция постоянна на [a, b]. Тогда 0)(xf во всех точках этого отрезка. Если же хотя бы одно из этих значений достигается внутри отрезка, то по теореме Ферма, производная функции в этой точке равна нулю: 0)(xf
По теореме Вейерштрасса, функция, непрерывная на отрезке, достигает на нем своего наибольшего М и наименьшего m значений. Если оба этих значения достигаются на концах отрезка, то они по условию равны: М= m , а это значит, что функция постоянна на [a, b]. Тогда 0)(xf во всех точках этого отрезка. Если же хотя бы одно из этих значений достигается внутри отрезка, то по теореме Ферма, производная функции в этой точке равна нулю: 0)(xf
 Найдется хотя бы одна точка, в которой касательная к графику функции параллельна оси Х, в этой точке производная функции будет равна нулю.
Найдется хотя бы одна точка, в которой касательная к графику функции параллельна оси Х, в этой точке производная функции будет равна нулю.
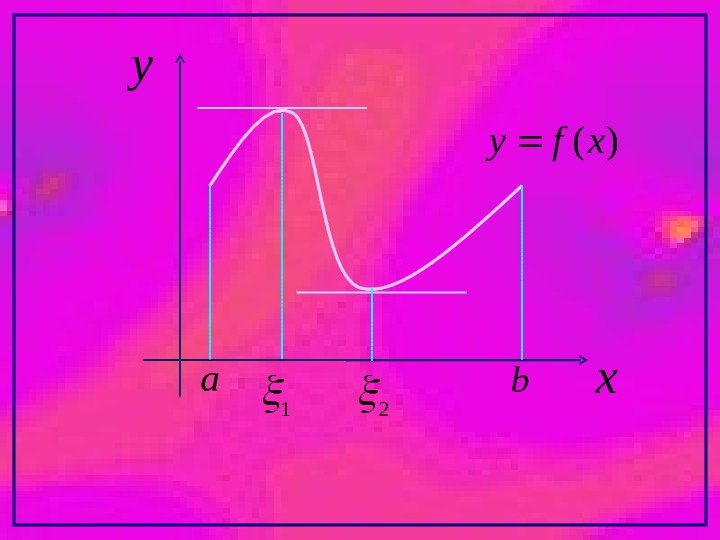 xy )(xfy ab
xy )(xfy ab
 Если же хотя бы одно условие теоремы Ролля нарушено, то заключение теоремы может быть неверным. Например: Отсутствует непрерывность на [a, b]. 1 xy)(xfy ab )(af )(bf
Если же хотя бы одно условие теоремы Ролля нарушено, то заключение теоремы может быть неверным. Например: Отсутствует непрерывность на [a, b]. 1 xy)(xfy ab )(af )(bf
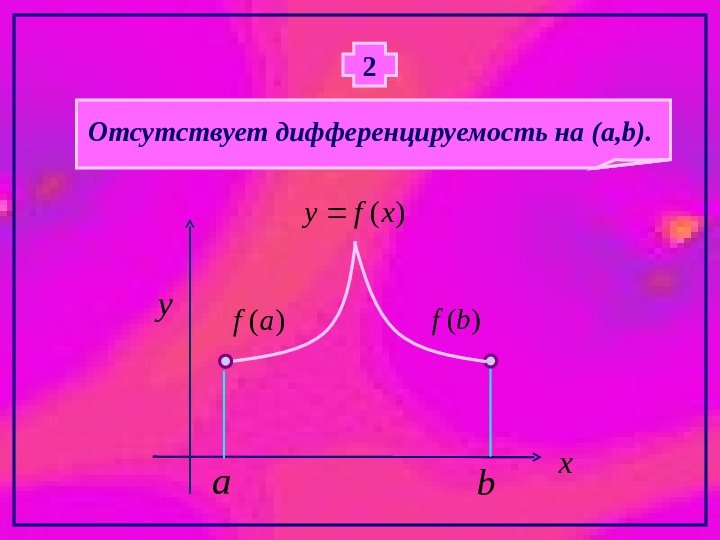
 Отсутствует дифференцируемость на ( a, b ). 2 x y )( xfy a b )(af)(bf
Отсутствует дифференцируемость на ( a, b ). 2 x y )( xfy a b )(af)(bf
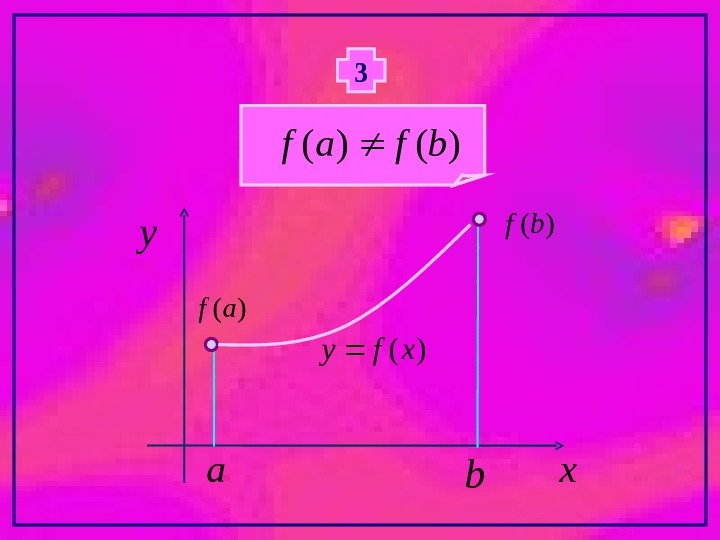
 3)()(bfaf x y )( xfy ab )(af )( bf
3)()(bfaf x y )( xfy ab )(af )( bf
![Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b]. Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b].](http://present5.com/presentforday2/20170128/8.9._images/8.9._11.jpg) Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b]. 2. Дифференцируема на интервале (a, b).
Пусть функция y=f(x) удовлетворяет следующим условиям: 1. Непрерывна на отрезке [a, b]. 2. Дифференцируема на интервале (a, b).
 Тогда внутри отрезка существует по крайней мере одна такая точка ξ , в которой производная функции равна частному от деления приращения функции на приращение аргумента на этом отрезке: ab afbf f )()( )(
Тогда внутри отрезка существует по крайней мере одна такая точка ξ , в которой производная функции равна частному от деления приращения функции на приращение аргумента на этом отрезке: ab afbf f )()( )(
 Введем новую функцию g(x) : Эта функция удовлетворяет всем условиям теоремы Ролля: Она непрерывна на [a, b] , дифференцируема на ( a, b ) и на концах отрезка принимает равные значения: )( )()(ax ab afbf xfxg )( )()(ab ab afbf bfbg
Введем новую функцию g(x) : Эта функция удовлетворяет всем условиям теоремы Ролля: Она непрерывна на [a, b] , дифференцируема на ( a, b ) и на концах отрезка принимает равные значения: )( )()(ax ab afbf xfxg )( )()(ab ab afbf bfbg
 )()()(afafbfbfbg )( )()(aa ab afbf afag 0 )()(afag)()(bgag. Следовательно, по теореме Ролля существует точка ), (ba такая, что 0)(g
)()()(afafbfbfbg )( )()(aa ab afbf afag 0 )()(afag)()(bgag. Следовательно, по теореме Ролля существует точка ), (ba такая, что 0)(g
 или 0)()()( a ab afbf fg 0 )()( ab afbf fg отсюда ab afbf f )()( )(
или 0)()()( a ab afbf fg 0 )()( ab afbf fg отсюда ab afbf f )()( )(
 Эту теорему часто записывают в виде: )()(afbfabf
Эту теорему часто записывают в виде: )()(afbfabf
 x y )(xfy ab
x y )(xfy ab
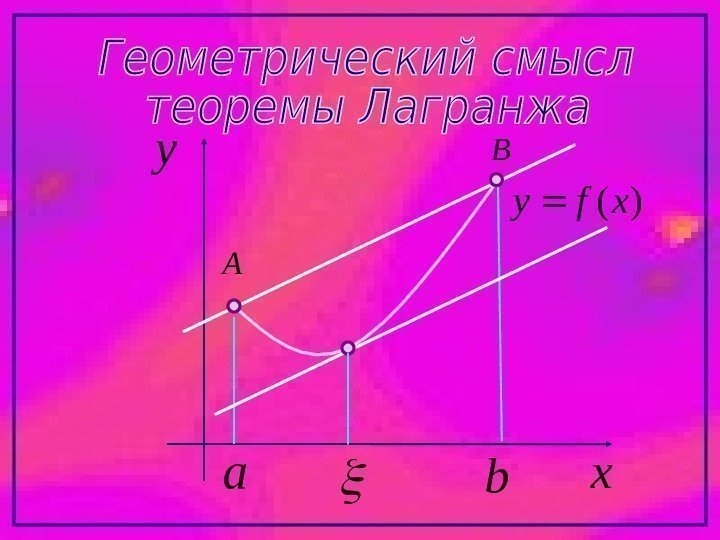
 Если перемещать прямую АВ параллельно начальному положению, то найдется хотя бы одна точка ), (ba в которой касательная к графику функции y=f(x) и хорда АВ, проведенная через концы дуги АВ будут параллельны.
Если перемещать прямую АВ параллельно начальному положению, то найдется хотя бы одна точка ), (ba в которой касательная к графику функции y=f(x) и хорда АВ, проведенная через концы дуги АВ будут параллельны.
 Если производная функции y=f(x) равна 0 на некотором промежутке Х, то эта функция постоянна на всем промежутке.
Если производная функции y=f(x) равна 0 на некотором промежутке Х, то эта функция постоянна на всем промежутке.
![Возьмем на промежутке Х [a, х ] , тогда по теореме Лагранжа)()(afxfaxf Возьмем на промежутке Х [a, х ] , тогда по теореме Лагранжа)()(afxfaxf](http://present5.com/presentforday2/20170128/8.9._images/8.9._20.jpg) Возьмем на промежутке Х [a, х ] , тогда по теореме Лагранжа)()(afxfaxf По условию теоремы 0)(f )()()(0 afxfax )()(0 afxf То есть )()(afxf
Возьмем на промежутке Х [a, х ] , тогда по теореме Лагранжа)()(afxfaxf По условию теоремы 0)(f )()()(0 afxfax )()(0 afxf То есть )()(afxf
