Скачать презентацию ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА Дифференциальное исчисление 1 Скачать презентацию ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА Дифференциальное исчисление 1

Л4 ПРОИЗВОДНАЯ ФСП.pptx

  • Количество слайдов: 15

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА Дифференциальное исчисление ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА Дифференциальное исчисление

§ 1. ПРОИЗВОДНАЯ ФУНКЦИИ 1. 1. Задачи, приводящие к понятию производной Скорость прямолинейного движения § 1. ПРОИЗВОДНАЯ ФУНКЦИИ 1. 1. Задачи, приводящие к понятию производной Скорость прямолинейного движения S(t) t ∆S ∆t S(t+∆t) t+∆t

Касательная к кривой ►Касательной к данной кривой в данной точке М называется предельное положение Касательная к кривой ►Касательной к данной кривой в данной точке М называется предельное положение секущей ММ 1, проходящей через точку М, когда вторая точка пересечения М 1 неограниченно приближается по кривой к точке М 1. Угловой коэффициент касательной равен

К нахождению пределов такого вида приводят решения и множества других задач. К нахождению пределов такого вида приводят решения и множества других задач.

1. 2. Определение производной. Механический и геометрический смысл производной. Пусть функция у=ƒ(х) определена на 1. 2. Определение производной. Механический и геометрический смысл производной. Пусть функция у=ƒ(х) определена на некотором интервале (a; b). ►Производной функции у=ƒ(х) в точке х0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю (если этот предел существует).

►Функция у=ƒ(х), имеющая производную в каждой точке интервала (a; b), называется дифференцируемой в этом ►Функция у=ƒ(х), имеющая производную в каждой точке интервала (a; b), называется дифференцируемой в этом интервале. ►Операция нахождения производной функции называется дифференцированием.

т. е. производная ƒ'(х) в точке х равна угловому коэффициенту касательной к графику т. е. производная ƒ'(х) в точке х равна угловому коэффициенту касательной к графику функции у = ƒ(х) в точке, абсцисса которой равна х. В этом заключается геометрический смысл производной. Если функция y=f(x) описывает какой-либо физический процесс, то производная у' есть скорость протекания этого процесса. В этом состоит физический смысл производной.

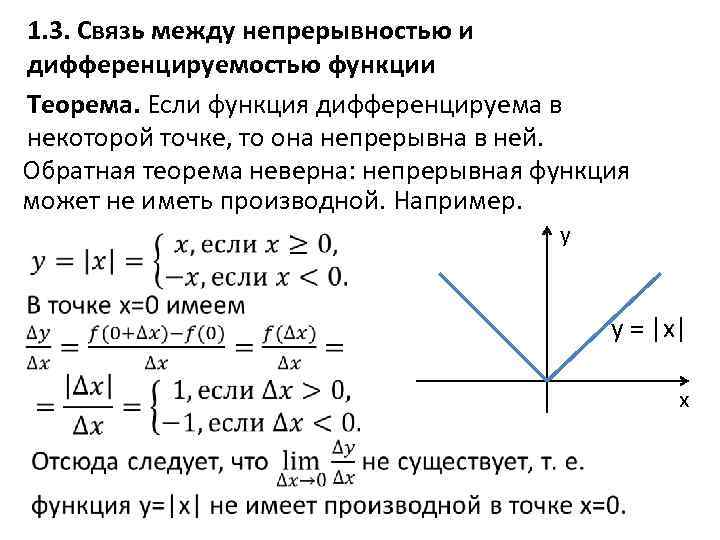1. 3. Связь между непрерывностью и дифференцируемостью функции Теорема. Если функция дифференцируема в некоторой 1. 3. Связь между непрерывностью и дифференцируемостью функции Теорема. Если функция дифференцируема в некоторой точке, то она непрерывна в ней. Обратная теорема неверна: непрерывная функция может не иметь производной. Например. y y = |x| x

1. 4. Основные правила дифференцирования Пусть функции f(x) и g(x) - две дифференцируемые в 1. 4. Основные правила дифференцирования Пусть функции f(x) и g(x) - две дифференцируемые в некотором интервале (a; b) функции.

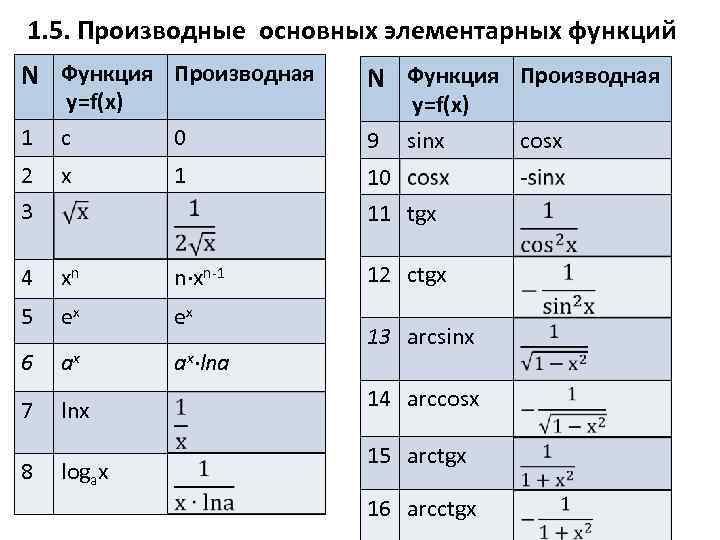1. 5. Производные основных элементарных функций N Функция Производная 1 с 0 9 2 1. 5. Производные основных элементарных функций N Функция Производная 1 с 0 9 2 3 x 1 10 11 tgx 4 xn n∙xn-1 12 ctgx 5 ex ex 6 ax ax∙lna 7 lnx y=f(x) 8 logax y=f(x) sinx 13 arcsinx 14 arccosx 15 arctgx 16 arcctgx cosx

1. 6. Производная сложной функции 1. 6. Производная сложной функции

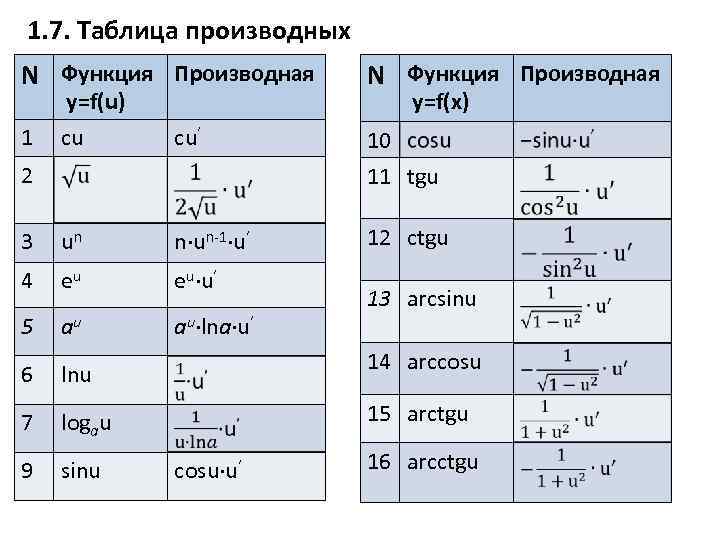1. 7. Таблица производных N Функция Производная 1 y=f(u) y=f(x) сu сu’ 10 11 1. 7. Таблица производных N Функция Производная 1 y=f(u) y=f(x) сu сu’ 10 11 tgu 3 un n∙un-1∙u’ 12 ctgu 4 eu eu∙u’ 5 au au∙lna∙u’ 6 lnu 7 logau 9 sinu 2 13 arcsinu 14 arccosu 15 arctgu cosu∙u’ 16 arcctgu

• Теорема. Пусть функции f(x) и g(x) : 1) определены и непрерывны в • Теорема. Пусть функции f(x) и g(x) : 1) определены и непрерывны в точке x 0 и ее окрестности; 2) дифференцируемые в точке x 0 и ее окрестности; 3) f(x 0) = g(x 0) =0, причем g’(x 0) ≠ 0.