Электричество и магнетизм. Лектор: Парахин А.















































elektrich1.pptx
- Размер: 1.2 Мб
- Автор:
- Количество слайдов: 51
Описание презентации Электричество и магнетизм. Лектор: Парахин А. по слайдам
 Электричество и магнетизм. • Лектор: • Парахин А. С. , к. ф. -м. наук, доцент.
Электричество и магнетизм. • Лектор: • Парахин А. С. , к. ф. -м. наук, доцент.
 1. Основные понятия. • 1. 1. Основные понятия. Закон Кулона. • Раздел физики «Электричество» изучает т. н. электрические явления. • Определение. Электрическими явлениями называются явления, связанные с взаимодействием и движением электрически заряженных тел.
1. Основные понятия. • 1. 1. Основные понятия. Закон Кулона. • Раздел физики «Электричество» изучает т. н. электрические явления. • Определение. Электрическими явлениями называются явления, связанные с взаимодействием и движением электрически заряженных тел.
 Электрический заряд. • Электрический заряд – неопределяемое понятие. Его можно только описать. • Тела приобретают заряд при трении, например, стекла о кожу. • Об этом можно судить по их возможности притягивать мелкие тела.
Электрический заряд. • Электрический заряд – неопределяемое понятие. Его можно только описать. • Тела приобретают заряд при трении, например, стекла о кожу. • Об этом можно судить по их возможности притягивать мелкие тела.
 Два типа заряда. • Из опыта также следует, что заряд приобретают оба трущихся тела. При этом между собой эти тела притягиваются, а две стеклянных палочки, потёртые о кожу, отталкиваются. Из этого следует вывод, что существует два вида заряда.
Два типа заряда. • Из опыта также следует, что заряд приобретают оба трущихся тела. При этом между собой эти тела притягиваются, а две стеклянных палочки, потёртые о кожу, отталкиваются. Из этого следует вывод, что существует два вида заряда.
 Взаимодействие зарядов. • Если тела заряжены одним и тем же видом заряда, они отталкиваются друг от друга, в противном случае притягиваются. Условно один вид заряда считают положительным электричеством, второй – отрицательным.
Взаимодействие зарядов. • Если тела заряжены одним и тем же видом заряда, они отталкиваются друг от друга, в противном случае притягиваются. Условно один вид заряда считают положительным электричеством, второй – отрицательным.
 Единица измерения заряда. • Для определённости стали считать, что при тернии стекла о кожу оно приобретает положительный заряд, а кожа отрицательный. Тогда знак заряда любого тела можно определить путём сравнения его со знаками заряда стекла или кожи, заряженных трением друг о друга. В системе СИ заряд измеряется в Кулона (Кл).
Единица измерения заряда. • Для определённости стали считать, что при тернии стекла о кожу оно приобретает положительный заряд, а кожа отрицательный. Тогда знак заряда любого тела можно определить путём сравнения его со знаками заряда стекла или кожи, заряженных трением друг о друга. В системе СИ заряд измеряется в Кулона (Кл).
 Электростатика. • Определение. Электростатикой называется раздел электричества, изучающий взаимодействие покоящихся электрических зарядов.
Электростатика. • Определение. Электростатикой называется раздел электричества, изучающий взаимодействие покоящихся электрических зарядов.
 Закон Кулона • Опыт показывает, что силы взаимодействия между заряженными телами зависят от расстояния. Тщательные эксперименты, выполненные Кулоном по исследованию силы взаимодействия зарядов, привели к закону, носящему имя Кулона • . Эта формула и носит название закона Кулона. •
Закон Кулона • Опыт показывает, что силы взаимодействия между заряженными телами зависят от расстояния. Тщательные эксперименты, выполненные Кулоном по исследованию силы взаимодействия зарядов, привели к закону, носящему имя Кулона • . Эта формула и носит название закона Кулона. •
 Обозначения. • Здесь — сила взаимодействия между зарядами, и величины взаимодействующих зарядов, а — расстояние между ними. •
Обозначения. • Здесь — сила взаимодействия между зарядами, и величины взаимодействующих зарядов, а — расстояние между ними. •
 Электростатическая константа. • Величина называется электрической постоянной и часто принимается равной • — также называется электростатической константой, она равна •
Электростатическая константа. • Величина называется электрической постоянной и часто принимается равной • — также называется электростатической константой, она равна •
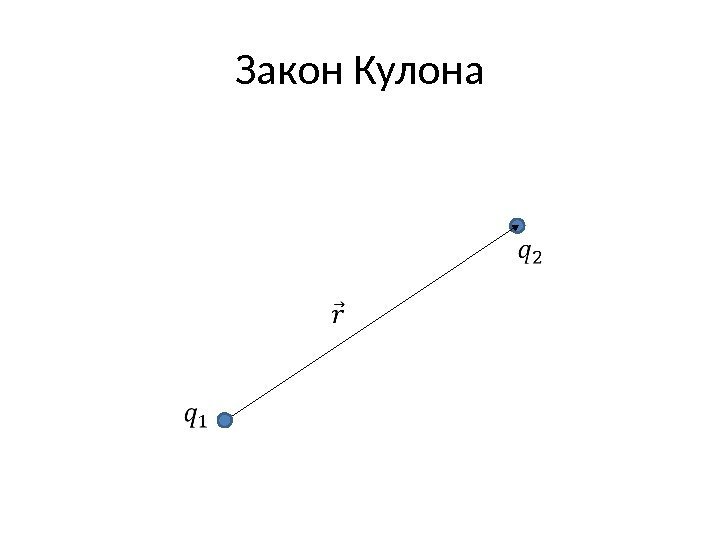
 Закон Кулона в векторной форме. • Кроме того, опыт показывает, что сила взаимодействия между точечными зарядами всегда направлена по прямой, соединяющей центры зарядов, т. е. по радиус-вектору от одного заряду к другому. Поэтому закон Кулона в векторном виде можно записать так •
Закон Кулона в векторной форме. • Кроме того, опыт показывает, что сила взаимодействия между точечными зарядами всегда направлена по прямой, соединяющей центры зарядов, т. е. по радиус-вектору от одного заряду к другому. Поэтому закон Кулона в векторном виде можно записать так •
 Закон Кулона
Закон Кулона
 Формулировка закона Кулона. • Этот закон гласит: «Сила, действующая на второй заряд со стороны первого, прямо пропорциональна величинам зарядов, обратно пропорциональна квадрату расстояния между ними и направлена по прямой, соединяющей центры зарядов» . • Сила, действующая на второй заряд со стороны первого, вычисляется по той же формуле, только радиус-вектор направлен уже от второго заряда к первому.
Формулировка закона Кулона. • Этот закон гласит: «Сила, действующая на второй заряд со стороны первого, прямо пропорциональна величинам зарядов, обратно пропорциональна квадрату расстояния между ними и направлена по прямой, соединяющей центры зарядов» . • Сила, действующая на второй заряд со стороны первого, вычисляется по той же формуле, только радиус-вектор направлен уже от второго заряда к первому.
 1. 2. Электрическое поле. Напряжённость электрического поля. • Вокруг заряда возникает силовое поле. Оно называется электрическим полем. • Определение. • Электрическое поле, создаваемое неподвижными зарядами называется электростатическим. • Электростатическое поле характерно тем, что его параметры с течением времени не меняются.
1. 2. Электрическое поле. Напряжённость электрического поля. • Вокруг заряда возникает силовое поле. Оно называется электрическим полем. • Определение. • Электрическое поле, создаваемое неподвижными зарядами называется электростатическим. • Электростатическое поле характерно тем, что его параметры с течением времени не меняются.
 Пробный заряд. • Определение. • Пробным зарядом называется положительный заряд, величина которого столь мала, что не искажает первоначальное электрическое поле и использующийся для исследования электрических полей.
Пробный заряд. • Определение. • Пробным зарядом называется положительный заряд, величина которого столь мала, что не искажает первоначальное электрическое поле и использующийся для исследования электрических полей.
 Сила пропорциональна заряду. • Опыт показывает, что сила, действующая на пробный заряд в электрическом поле, прямо пропорциональна величине пробного заряда. Это значит, что эта сила сама по себе не может служить характеристикой поля.
Сила пропорциональна заряду. • Опыт показывает, что сила, действующая на пробный заряд в электрическом поле, прямо пропорциональна величине пробного заряда. Это значит, что эта сила сама по себе не может служить характеристикой поля.
 Отношение силы к заряду • Если же силу разделить на пробный заряд, получится величина, которая от пробного заряда уже не зависит. Она и может служить характеристикой поля.
Отношение силы к заряду • Если же силу разделить на пробный заряд, получится величина, которая от пробного заряда уже не зависит. Она и может служить характеристикой поля.
 Напряжённость электрического поля. • Определение. Напряжённостью электрического поля в данной точке пространства называется физическая величина, равная силе действующей на единицу заряда, помещённого в данную точку пространства. •
Напряжённость электрического поля. • Определение. Напряжённостью электрического поля в данной точке пространства называется физическая величина, равная силе действующей на единицу заряда, помещённого в данную точку пространства. •
 Следствия из определения. • 1. Напряжённость есть векторная величина. Она направлена в сторону действия силы. • 2. Размерность. •
Следствия из определения. • 1. Напряжённость есть векторная величина. Она направлена в сторону действия силы. • 2. Размерность. •
 Однородное поле. • Определение. • Если напряжённость электрического поля не зависит от координат точки, поле называется однородным.
Однородное поле. • Определение. • Если напряжённость электрического поля не зависит от координат точки, поле называется однородным.
 Силовые линии электрического поля. • Определение. • Кривая в пространстве, касательная в каждой точке к которой совпадает по направлению с вектором напряжённости электрического поля называется силовой линией. • Силовые линии используются для наглядного представления различных силовых полей
Силовые линии электрического поля. • Определение. • Кривая в пространстве, касательная в каждой точке к которой совпадает по направлению с вектором напряжённости электрического поля называется силовой линией. • Силовые линии используются для наглядного представления различных силовых полей
 Пробный заряд в поле точечного заряда. • Если пробный заряд помещён в поле, создаваемое точечным зарядом, то согласно закону Кулона, сила, действующая на пробный заряд, равна: • •
Пробный заряд в поле точечного заряда. • Если пробный заряд помещён в поле, создаваемое точечным зарядом, то согласно закону Кулона, сила, действующая на пробный заряд, равна: • •
 Напряжённость поля точечного заряда. • Тогда напряжённость поля точечного заряда может быть найдена по формуле: • Если заряд положителен, напряжённость направлена от заряда, если отрицателен – к заряду. •
Напряжённость поля точечного заряда. • Тогда напряжённость поля точечного заряда может быть найдена по формуле: • Если заряд положителен, напряжённость направлена от заряда, если отрицателен – к заряду. •
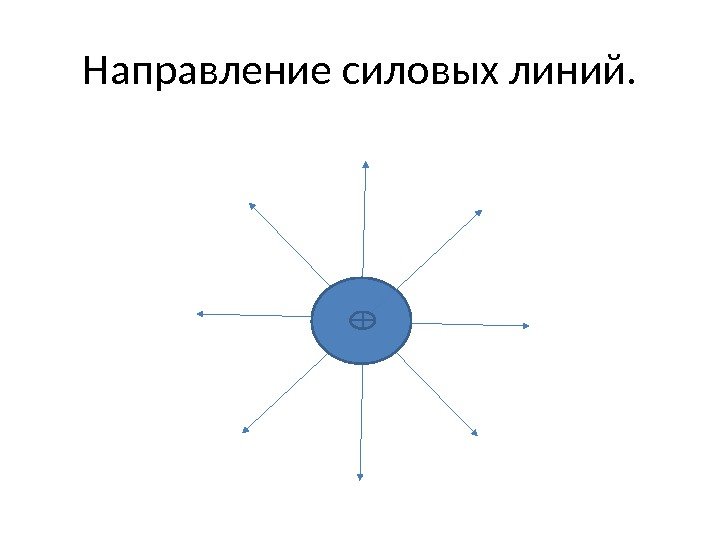
 Направление силовых линий.
Направление силовых линий.
 Суперпозиция сил. • Если в данной точке пространства присутствуют несколько полей, то на пробный заряд действуют несколько сил. Согласно принципу суперпозиции сил, результирующая силы будет равна сумме сил, действующих со стороны каждого поля: •
Суперпозиция сил. • Если в данной точке пространства присутствуют несколько полей, то на пробный заряд действуют несколько сил. Согласно принципу суперпозиции сил, результирующая силы будет равна сумме сил, действующих со стороны каждого поля: •
 Суперпозиция полей. • Разделив эту силу на величину пробного заряда, получим напряжённость результирующего поля: •
Суперпозиция полей. • Разделив эту силу на величину пробного заряда, получим напряжённость результирующего поля: •
 Формулировка принципа суперпозиции полей. • Это равенство носит название принципа суперпозиции для напряжённости электрического поля. Он гласит: • Напряжённость результирующего электрического поля, состоящего из нескольких полей, равна сумме напряжённостей складываемых полей.
Формулировка принципа суперпозиции полей. • Это равенство носит название принципа суперпозиции для напряжённости электрического поля. Он гласит: • Напряжённость результирующего электрического поля, состоящего из нескольких полей, равна сумме напряжённостей складываемых полей.
 1. 3. Работа электрического поля, потенциальная энергия заряда в электрическом поле, потенциал. • Напряжённость электрического поля есть силовая характеристика поля. Однако поле обладает некоторой потенциальной энергией, поэтому обладает и некоторой энергетической характеристикой.
1. 3. Работа электрического поля, потенциальная энергия заряда в электрическом поле, потенциал. • Напряжённость электрического поля есть силовая характеристика поля. Однако поле обладает некоторой потенциальной энергией, поэтому обладает и некоторой энергетической характеристикой.
 Работа электростатических сил. • Найдём работу, совершаемую силами, действующими на пробный заряд со стороны электрического поля. • Найдём эту работу для поля точечного заряда, т. е. для силы •
Работа электростатических сил. • Найдём работу, совершаемую силами, действующими на пробный заряд со стороны электрического поля. • Найдём эту работу для поля точечного заряда, т. е. для силы •
 Формула работы поля точечного заряда. • Тогда формула работы будет иметь вид: • Здесь – элементарное перемещение пробного заряда по траектории. •
Формула работы поля точечного заряда. • Тогда формула работы будет иметь вид: • Здесь – элементарное перемещение пробного заряда по траектории. •
 Схема расчёта. • Как видно из рисунка: •
Схема расчёта. • Как видно из рисунка: •
 Работа по перемещению пробного заряда. • Поэтому работу электрического поля можно найти следующим образом •
Работа по перемещению пробного заряда. • Поэтому работу электрического поля можно найти следующим образом •
 Потенциальность электростатического поля. • Отсюда видно, что работа электростатического поля точечного заряда не зависит от пути движения пробного заряда, а зависит лишь от начального и конечного состояний. Это значит, что электростатическое поле потенциально. Поскольку любое электростатическое поле есть поле, создаваемое системой точечных зарядов, любое электростатическое поле потенциально.
Потенциальность электростатического поля. • Отсюда видно, что работа электростатического поля точечного заряда не зависит от пути движения пробного заряда, а зависит лишь от начального и конечного состояний. Это значит, что электростатическое поле потенциально. Поскольку любое электростатическое поле есть поле, создаваемое системой точечных зарядов, любое электростатическое поле потенциально.
 Потенциальная энергия взаимодействия зарядов. • В качестве потенциальной энергии можно выбрать величину: • тогда работу можно выразить, как убыль потенциальной энергии •
Потенциальная энергия взаимодействия зарядов. • В качестве потенциальной энергии можно выбрать величину: • тогда работу можно выразить, как убыль потенциальной энергии •
 Зависимость потенциальной энергии от величины пробного заряда. • Как видно из формулы потенциальной энергии, потенциальная энергия прямо пропорциональна величине пробного заряда. Это значит, что потенциальная энергия зависит не только от поля, но и от величины пробного заряда. Поэтому она не может быть характеристикой только поля.
Зависимость потенциальной энергии от величины пробного заряда. • Как видно из формулы потенциальной энергии, потенциальная энергия прямо пропорциональна величине пробного заряда. Это значит, что потенциальная энергия зависит не только от поля, но и от величины пробного заряда. Поэтому она не может быть характеристикой только поля.
 Потенциал • Если разделить потенциальную энергию на величину пробного заряда, получим величину, которая от пробного заряда уже не зависит. Она и может играть роль энергетической характеристики самого поля. Эта величина и носит название потенциала.
Потенциал • Если разделить потенциальную энергию на величину пробного заряда, получим величину, которая от пробного заряда уже не зависит. Она и может играть роль энергетической характеристики самого поля. Эта величина и носит название потенциала.
 Определение потенциала. • Определение. • Физическая величина численно равная потенциальной энергии единицы пробного заряда, называется потенциалом поля в данной точке и обозначается. •
Определение потенциала. • Определение. • Физическая величина численно равная потенциальной энергии единицы пробного заряда, называется потенциалом поля в данной точке и обозначается. •
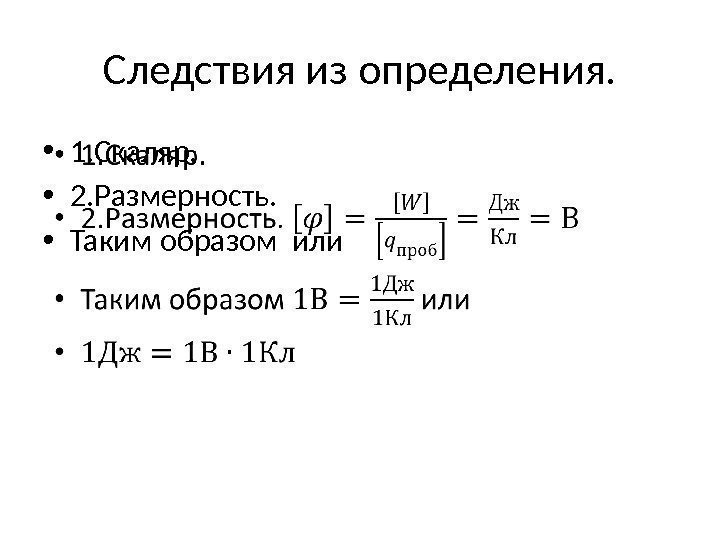
 Следствия из определения. • 1. Скаляр. • 2. Размерность. • Таким образом или •
Следствия из определения. • 1. Скаляр. • 2. Размерность. • Таким образом или •
 Электрон-вольт • Электрон-вольт – это изменение энергии электрона, прошедшего разность потенциалов 1 В.
Электрон-вольт • Электрон-вольт – это изменение энергии электрона, прошедшего разность потенциалов 1 В.
 Эквипотенциальная поверхность. • Определение. • Поверхность в пространстве, соответствующая одному и тому же значению потенциала, называется эквипотенциальной поверхностью. • Для поля точечного заряда эквипотенциальные поверхности есть сферы с центом в центре заряда.
Эквипотенциальная поверхность. • Определение. • Поверхность в пространстве, соответствующая одному и тому же значению потенциала, называется эквипотенциальной поверхностью. • Для поля точечного заряда эквипотенциальные поверхности есть сферы с центом в центре заряда.
 Примеры эквипотенциальных поверхностей. • Для поля точечного заряда эквипотенциальные поверхности есть сферы с центом в центре заряда. • Для однородного поля эквипотенциальные поверхности есть плоскости, перпендикулярные к вектору напряжённости электрического поля.
Примеры эквипотенциальных поверхностей. • Для поля точечного заряда эквипотенциальные поверхности есть сферы с центом в центре заряда. • Для однородного поля эквипотенциальные поверхности есть плоскости, перпендикулярные к вектору напряжённости электрического поля.
 Связь силы и потенциальной энергии. • С помощью потенциальной энергии можно выразить и силу, действующую на пробный заряд • откуда в свою очередь можно выразить напряжённость электрического поля. •
Связь силы и потенциальной энергии. • С помощью потенциальной энергии можно выразить и силу, действующую на пробный заряд • откуда в свою очередь можно выразить напряжённость электрического поля. •
 Связь потенциала с напряжённостью. • Для этого разделим предыдущее равенство на пробный заряд: • Но – есть напряжённость электрического поля, а • – есть потенциал поля, так что: •
Связь потенциала с напряжённостью. • Для этого разделим предыдущее равенство на пробный заряд: • Но – есть напряжённость электрического поля, а • – есть потенциал поля, так что: •
 Потенциальная энергия заряда в поле. • С помощью понятия потенциала потенциальную энергию любого заряда в электростатическом поле можно выразить следующим образом: • А работу по перемещению заряда в поле можно найти по формуле: •
Потенциальная энергия заряда в поле. • С помощью понятия потенциала потенциальную энергию любого заряда в электростатическом поле можно выразить следующим образом: • А работу по перемещению заряда в поле можно найти по формуле: •
 Потенциал поля точечного заряда. • Для точечного заряда потенциал можно найти по формуле: •
Потенциал поля точечного заряда. • Для точечного заряда потенциал можно найти по формуле: •
 Определение разности потенциалов • Если известна напряжённость электрического поля, как функция координат, то потенциал поля можно найти путём интегрирования напряжённости поля: • . •
Определение разности потенциалов • Если известна напряжённость электрического поля, как функция координат, то потенциал поля можно найти путём интегрирования напряжённости поля: • . •
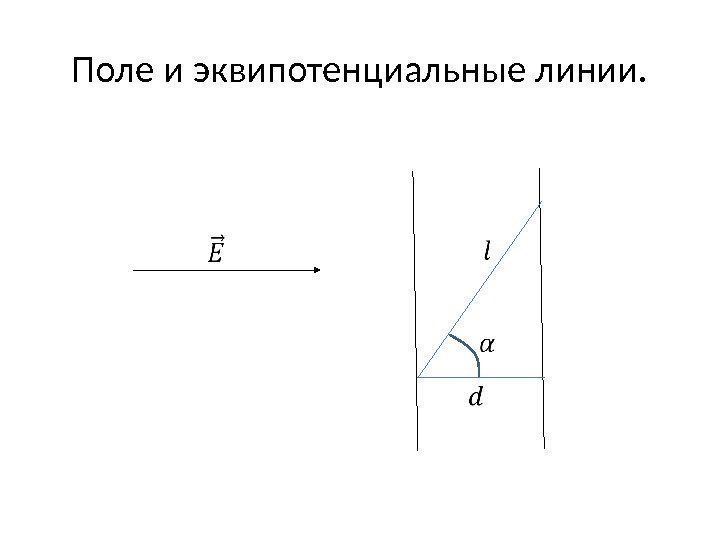
 Потенциал однородного поля • Если напряжённость поля постоянная величина, её можно вынести за знак интеграла • – угол между напряжённостью электрического поля и перемещением. •
Потенциал однородного поля • Если напряжённость поля постоянная величина, её можно вынести за знак интеграла • – угол между напряжённостью электрического поля и перемещением. •
 Поле и эквипотенциальные линии.
Поле и эквипотенциальные линии.
 Разность потенциалов в однородном поле. • есть расстояние между двумя плоскостями, перпендикулярными напряжённости электрического поля и проходящими через точки, в которых находится разность потенциалов. Это есть расстояние между двумя эквипотенциальными поверхностями. Тогда •
Разность потенциалов в однородном поле. • есть расстояние между двумя плоскостями, перпендикулярными напряжённости электрического поля и проходящими через точки, в которых находится разность потенциалов. Это есть расстояние между двумя эквипотенциальными поверхностями. Тогда •
 Потенциальная энергия суммы полей. • Если электрическое поле представляет наложение нескольких полей, то потенциальная энергия пробного заряда в результирующем поле будет равна сумме потенциальных энергий заряда в каждом из полей.
Потенциальная энергия суммы полей. • Если электрическое поле представляет наложение нескольких полей, то потенциальная энергия пробного заряда в результирующем поле будет равна сумме потенциальных энергий заряда в каждом из полей.
 Принцип суперпозиции для потенциала • Отсюда следует т. н. принцип суперпозиции и для потенциала: потенциал результирующего поля, состоящего из нескольких полей, равен сумме потенциалов складываемых полей.
Принцип суперпозиции для потенциала • Отсюда следует т. н. принцип суперпозиции и для потенциала: потенциал результирующего поля, состоящего из нескольких полей, равен сумме потенциалов складываемых полей.
