Экономико-Математическое моделирование Основные понятия математического моделирования Модель

Экономико-Математическое моделирование

Основные понятия математического моделирования Модель – это материальный или мысленно представляемый объект, который в процессе исследования замещает объекторигинал так, что его непосредственное изучение дает новые знания об объекте-оригинале. Процесс построения, изучения и применения моделей называется моделированием. Моделирование в экономике – это воспроизведение экономических объектов и процессов в ограниченных, малых экспериментальных формах, в искусственно созданных условиях. В экономике чаще используется математическое моделирование посредством описания экономических процессов математическими зависимостями. Моделирование служит предпосылкой и средством анализа экономики и протекающих в ней явлений, а также методом обоснования принимаемых решений, прогнозирования, планирования, управления экономическими процессами и объектами. Модель экономического объекта обычно поддерживается реальными статистическими и эмпирическими данными, а результаты расчетов, выполненные в рамках построенной модели, позволяют строить прогнозы и давать объективные оценки исследуемых объектов.

Объектом моделирования может быть либо реальная хозяйственная система, либо один или несколько процессов, протекающих в ней. Для построения модели необходимо не просто выбрать объект, но и дать его описание в виде системы, т. е. определить границы его взаимодействия с внешней средой, его структуру. Модели одного и того же объекта могут быть различными и отражать этот объект с разных сторон. Экономико-математические модели – это смешанные модели, включающие в себя совокупность математических зависимостей, логических построений, схем, графиков и т. д. , связанных в некоторую единую систему, имеющую экономический смысл. Экономико-математические методы – комплекс экономических и математических научных дисциплин, объединенных для изучения социально-экономичсеких систем и процессов. Экономико-математическое моделирование – описание экономических и социальных систем и процессов в виде экономикоматематических моделей.

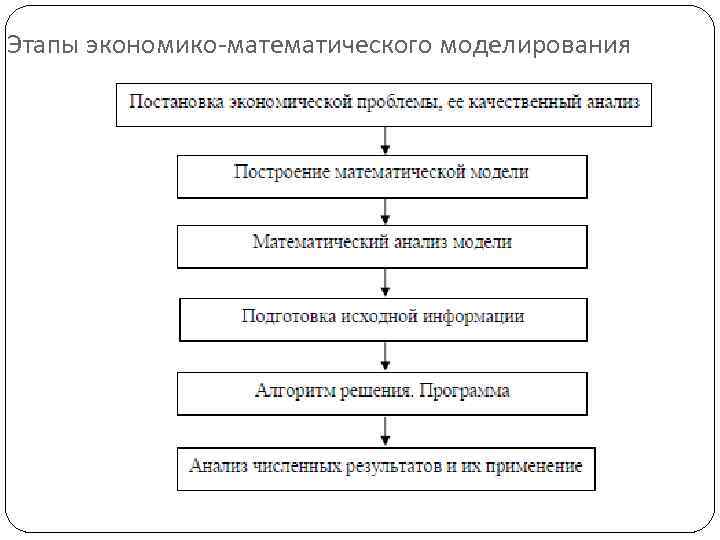Этапы экономико-математического моделирования

Рассмотрим каждый из этапов более подробно. 1. Постановка экономической проблемы и ее качественный анализ. На этом этапе требуется сформулировать сущность проблемы, принимаемые предпосылки и допущения. Необходимо выделить важнейшие черты и свойства моделируемого объекта, изучить его структуру и взаимосвязь его элементов, хотя бы предварительно сформулировать гипотезы, объясняющие поведение и развитие объекта. 2. Построение математической модели. Это этап формализации экономической проблемы, т. е. выражения ее в виде конкретных математических зависимостей (функций, уравнений, неравенств и др. ). Построение модели подразделяется в свою очередь на несколько стадий. Сначала определяется тип экономико-математической модели, изучаются возможности ее применения в данной задаче, уточняются конкретный перечень переменных и параметров и форма связей. 3. Математический анализ модели. На этом этапе чисто математическими приемами исследования выявляются общие свойства модели и ее решений. В частности, важным моментом является доказательство существования решения сформулированной задачи. При аналитическом исследовании выясняется, единственно ли решение, какие переменные могут входить в решение, в каких пределах они изменяются, каковы тенденции их изменения и т. д. Однако модели сложных экономических объектов с большим трудом поддаются аналитическому исследованию; в таких случаях переходят к численным методам исследования.

4. Подготовка исходной информации. В экономических задачах это, как правило, наиболее трудоемкий этап моделирования, так как дело не сводится к пассивному сбору данных. Математическое моделирование предъявляет жесткие требования к системе информации; при этом надо принимать во внимание не только принципиальную возможность подготовки информации требуемого качества, но и затраты на подготовку информационных массивов. В процессе подготовки информации используются методы теории вероятностей, теоретической и математической статистики для организации выборочных обследований, оценки достоверности данных и т. д. При системном экономикоматематическом моделировании результаты функционирования одних моделей служат исходной информацией для других. 5. Алгоритм решения. Программа включает разработку алгоритмов численного решения задачи, подготовку программ на ЭВМ и непосредственное проведение расчетов; при этом значительные трудности вызываются большой размерностью экономических задач. Обычно расчеты на основе экономикоматематической модели носят многовариантный характер.

6. Анализ численных результатов и их применение. На этом этапе прежде всего решается важнейший вопрос о правильности и полноте результатов моделирования и применимости их как в практической деятельности, так и в целях усовершенствования модели. Поэтому в первую очередь должна быть проведена проверка адекватности модели по тем свойствам, которые выбраны в качестве существенных. Применение численных результатов моделирования в экономике направлено на решение практических задач (анализ экономических объектов, экономическое прогнозирование развития хозяйственных и социальных процессов, выработка управленческих решений на всех уровнях хозяйственной иерархии). Перечисленные этапы экономико-математического моделирования находятся в тесной взаимосвязи, в частности, могут иметь место возвратные связи этапов. Недостатки, которые не удается исправить на тех или иных этапах моделирования, устраняются в последующих циклах. Однако результаты каждого цикла имеют и вполне самостоятельное значение. Начав исследование с построения простой модели, можно получить полезные результаты, а затем перейти к созданию более сложной и более совершенной модели, включающей в себя новые условия и более точные математические зависимости.

Классификация экономико-математических моделей Единой системы классификации таких моделей в настоящее время также не существует, однако обычно выделяют более десяти основных признаков их классификаций. По общему целевому назначению экономико-математические модели делятся на: – теоретико-аналитические, используемые при изучении общих свойств и закономерностей, экономических процессов; – прикладные, применяемые в решении конкретных экономических задач анализа прогнозирования и управления. Прикладные модели дают возможность оценить параметры функционирования конкретного экономического объекта и сформулировать рекомендации для принятия практических решений. К прикладным моделям относятся прежде всего эконометрические модели, оперирующие числовыми значениями экономических переменных и позволяющие статистически значимо оценивать их на основе имеющихся наблюдений. По степени агрегирования объектов моделирования модели разделяются на: – макроэкономические – модели, отражающие функционирование экономики как единого целого; – микроэкономические – модели, описывающие взаимодействие структурных и функциональных составляющих экономики либо поведение отдельной такой составляющей в рыночной среде (предприятия или фирмы).

По конкретному предназначению (по цели создания и применения) выделяют: – балансовые модели, выражающие требование соответствия наличия ресурсов и их использования; – трендовые модели, в которых развитие моделируемой экономической системы отражается через тренд (длительную тенденцию) ее основных показателей; – оптимизационные модели, предназначенные для выбора наилучшего варианта из определенного числа вариантов производства, распределения или потребления; – имитационные модели, предназначенные для использования в процессе машинной имитации изучаемых систем или процессов и др. По типу информации, используемой в модели, экономико-математические модели делятся на: – аналитические, построенные на априорной информации; – идентифицируемые, построенные на апостериорной информации. По учету фактора времени модели подразделяются на: – статические, в которых все зависимости отнесены к одному моменту времени. В статических моделях обычно зафиксированы значения ряда величин, являющихся переменными в динамике, – например, капитальных ресурсов, цен и т. п. ; – динамические, описывающие экономические системы в развитии. Динамическая модель не сводится к простой сумме ряда статических, а описывает силы и взаимодействия в экономике, определяющие ход процессов в ней. Динамические модели обычно используют аппарат дифференциальных и разностных уравнений, вариационного исчисления.

По учету фактора неопределенности модели распадаются на: – детерминированные, если в них результаты на выходе однозначно определяются управляющими воздействиями. Детерминированные модели предполагают жесткие функциональные связи между переменными; – стохастические (вероятностные), если при задании на входе модели определенной совокупности значений на ее выходе могут получаться различные результаты в зависимости от действия случайного фактора. Для описания таких моделей используют инструментарий теории вероятностей и математической статистики. По типу математического аппарата, используемого в модели, выделяют: – матричные модели, – модели линейного и нелинейного программирования, – корреляционно-регрессионные модели, – модели теории массового обслуживания, – модели сетевого планирования и управления, – модели теории игр и т. д. По типу подхода к изучаемым социально-экономическим системам выделяют: – дескриптивный (описательный). При дескриптивном подходе получаются модели, предназначенные для описания и объяснения фактически наблюдаемых явлений или для прогноза этих явлений; в качестве примера дескриптивных моделей можно привести, названные ранее балансовые и трендовые модели. – нормативные модели. При нормативном подходе интересуются не тем, каким образом устроена и развивается экономическая система, а как она должна быть устроена и как должна действовать в смысле определенных критериев. В частности, все оптимизационные модели относятся к типу нормативных; другим примером могут служить нормативные модели уровня жизни.

История экономико-математической идеи Моделирование, как метод научного познания, стало применяться еще в глубокой древности и постепенно захватило все новые области научных познаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и , наконец, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования XX век. Однако методология моделирования долгое время развивалась независимо отдельными науками. Отсутствовала единая система понятий, единая терминология. Лишь постепенно стала осознаваться важная роль моделирования как универсального метода научного познания.

Применение математических методов, в том числе и методов математического моделирования, в экономике в целом имеет длительную историю. В качестве примера приведем характеристику математического метода исследования основателем классической школы буржуазной политической экономии В. Петти (1623 – 1687). В предисловии к «Политической арифметике» В. Петти указывал, что его способ исследования «не обычный, ибо вместо того, чтобы употреблять слова только в сравнительной и превосходной степени и прибегать к умозрительным аргументам, я вступил на путь выражения своих мнений на языке чисел, весов и мер, что я уже давно стремился пойти по этому пути, чтобы показать пример политической арифметики» . Революционный демократ, крупнейший экономист домарксовского периода Н. Г. Чернышевский (1828 – 1889) в замечаниях на трактат Д, С. Миля «Основания политической экономии» писал: «Мы видели уже много примеров тому, какими приемами пользуется политическая экономия для решения своих задач. Эти приемы математические. Иначе и быть не может, потому что предмет науки – количества, подлежащие счету и мере, понимаемые только через вычисление и измерение» .

Понятие об экономике как науке возникло в период расцвета греческой рабовладельческой демократии, когда были сделаны первые попытки не просто заметить, а теоретически осмыслить факты экономической жизни. По своему основному содержанию она должна была заниматься вопросами рационального хозяйствования. Однако поскольку богатое греческое рабовладельческое хозяйство являлось сложной производственной системой, на которой отражались все процессы, происходившие в обществе, то эта наука неизбежно затрагивала и более общие проблемы: из каких хозяйственных единиц должно состоять разумно построенное государство; в каком отношении эти единицы должны обменивать производимые ими товары; какую роль играют торговля и деньги? Проблемы экономической науки в таком виде сформулировал великий греческий философ Аристотель, которого принято считать ее основателем. Аристотель первым пытался рассмотреть экономические закономерности, господствующие в обществе, выдвинул идею о различии между потребительной и меновой стоимостями товаров, высказал мысль о превращении денег в капитал и т. д. Таким образом, еще в Древней Греции в экономической науке возникли два направления исследований: во-первых, это анализ методов рационального управления народным хозяйством и, во-вторых, изучение основных экономических закономерностей.

В дальнейшем первое направление превратилось в науку о рациональном управлении деятельностью производительных единиц любого уровня - от производственного участка до экономики в целом. Второе направление дало начало экономической теории - науке, изучающей основные экономические закономерности сменяющих друга общественноэкономических формаций. Оба направления экономической науки развивались и развиваются в тесной связи между собой, их общность особенно заметна в исследованиях, направленных на изучение экономики страны как целого. В системе экономических наук главенствующее положение занимает экономическая теория: она служит теоретической и методологической основой всего комплекса экономических наук. Применение математических методов в экономике началось именно в теоретикоэкономических исследованиях. Обычно в качестве исторически первой модели общественного производства называют экономическую таблицу Ф. Кене (1694 - 1774). В 1758 г. он опубликовал первый вариант своей «Экономической таблицы» , второй вариант - «Арифметическая формула» - был опубликован в 1766 году. К. Маркс высоко оценил таблицу Ф. Кенэ. «Это попытка, - писал Маркс, - сделанная во второй трети XIII столетия, в период детства политической экономии, была в высшей степени гениальной идеей, бесспорно самой гениальной из всех, какие только выдвинула до сего времени политическая экономия» .

Математическая школа возникла в рамках так называемого неоклассического направления в политической экономии, главным содержанием которого является теория предельной полезности (маржинализм). В ходе развитие неоклассического направления проблемы социально-экономической динамики незаметно исчезают из анализа, постепенно осуществляется переход к общим проблемам функционирования экономических систем, рыночных и ценовых механизмов, реализации принципа экономичности и рациональности в условиях совершенной конкуренции, условий частного и общего равновесия. Родоначальником математической школы считается французский ученый О. Курно (1801 - 1877). В 1838 г. вышла его книга «Исследование математических принципов теории богатства» (О. Курно был известным математиком, философом, историком и экономистом). Видными представителями математической школы являются Г. Госсен (1810 - 1859) в Германии, В. Джевонс (1835 - 1882) в Англии, Л. Вальрас (1834 - 1910) в Швейцарии, Г. Кассель (1866 - 1944) в Швеции, Ф. Эджворд (1845 - 1926) в Англии, В. Парето (1848 - 1923) в Италии, В. Дмитриев) 1868 - 1913) в России. Представители математического направления в буржуазной политической экономии достигли известных успехов в области математического моделирования, в раскрытии ряда объективных закономерностей производства, обмена, распределения и потребления. В этой связи необходимо отметить важность работ русского экономиста В. К. Дмитриева. Его основная работа «Экономические очерки. Опыт органического синтеза трудовой ценности и теории предельной полезности» была опубликована в 1904 году. В своих работах В, К. Дмитриев предвосхитил ряд выводов, которые позднее были получены В. Леонтьевым на основе анализа моделей «затраты - выпуск» . В частности, эти выводы важны для подсчета коэффициентов полных материальных и трудовых затрат. Кроме того, стремясь примирить трудовую теорию стоимости с теорией предельной полезности, что, естественно, сделать невозможно, он тем не менее поставил проблему соотношения категорий стоимости и полезности.

Родоначальники математической школы рассматривали математические методы, математическое моделирование связей между элементами экономической системы как методы исследования, а не как методы изложения, иллюстраций экономических положений и законов, полученных других путем. Изложение же выводов, полученных математически, может быть дано и на обычном языке, или в математической форме, но без доказательства. Так, Л. Вальрас писал: «Весьма немногие из нас в состоянии прочесть «Математические начала натуральной философии» Ньютона или «Небесную механику» Лапласа, и тем не менее мы все принимаем на веру сделанное сведущими людьми описание мира астрономических явлений согласно закону всеобщего тяготения. Почему точно таким же образом не принять описание мира экономических явлений, сделанного согласно закону свободной конкуренции» . Представители математической школы с помощью математических методов стремились разрешить не отдельные частные проблемы экономической теории, а охватить весь экономический процесс в целом, дать общую картину взаимозависимости всех экономических явлений. Так, по мнению Парето, процесс научного прогресса проходит через три стадии: мы ограничиваемся констатированием существованиям взаимодействия между отдельными элементами экономической системы, не входя в дальнейшее их изучение; мы знаем отдельные связи, существующие между отдельными элементами; мы имеем возможность вычислить величину всех этих элементов и дать совершенно точное выражение условий равновесия. Идеал всякой науки - достижение третьей стадии. Математический метод рассматривается как основной, важнейший метод, который только один в состоянии дать экономической теории научную законченность.

Важное место в развитии математического направления в экономике занимают работы советских ученых: Л. В. Канторовича, В. В. Новожилова, В. С. Немчинова, В. Леонтьева. В 1936 г. В. Леонтьев опубликовал основы метода (модели) «затраты - выпуск» . В. Леонтьеву хорошо были известны работы советских экономистов по балансу народного хозяйства за 1923 -1924 гг. , в основу которого были положены идеи схем воспроизводства К. Маркса. В качестве исходного момента В. Леонтьев использовал модель общего экономического равновесия Л. Вальраса, прежде всего идею технических коэффициентов. Формирование цен в рамках модели трактуется с позиций неоклассической теории стоимости. Система цен в модели при ограничении только на один первичный фактор - труд - обеспечивает нулевую прибыль, прибавочная стоимость отсутствует, весь национальный доход реализуется только на заработную плату. При наличии ограничений и на основной капитал в структуре цены появляется норма процента. Трактовка модели и ее категорий ведется с позиции неоклассической теории производительности факторов производства при отсутствии взаимозаменяемости между ними.

Работа Л. В. Канторовича «Математические методы организации и планирования производства» (Ленинград, 1939 г. ) положила начало новому направлению в математической экономии - методам линейного программирования, метода математического программирования. Канторович в результате анализа некоторых задач планирования производства сформулировал новый важный для экономики класс математических задач, получивших название задач линейного программирования. В линейном программировании рассматривается вопрос о поиске среди всех допустимых решений, удовлетворяющих системе линейных равенств или неравенств, наилучшего (оптимального) решения, доставляющего максимум (минимум) некоторому линейному критерию. Его работа «Экономический расчет наилучшего использования ресурсов» вышла двумя изданиями в 1959 г. и 1960 г. и была переведена на французский, английский, испанский и другие языки. Работы В. В. Новожилова, в частности «Проблемы измерения затрат и результатов при оптимальном планировании» , обосновали решающую роль ценообразования, механизма распределения капиталовложений, согласования народнохозяйственных и хозрасчетных интересов для оптимизации всего общественного производства. Работа В. С. Немчинова «Экономико-математический методы и модели» (1962) имела важное научное, учебное и методологическое значение для развития экономико-математических исследований в нашей стране.

Управление запасами. Модель Уилсона. Математические модели управления запасами (УЗ) позволяют найти оптимальный уровень запасов некоторого товара, минимизирующий суммарные затраты на покупку, оформление и доставку заказа, хранение товара, а также убытки от его дефицита. Модель Уилсона является простейшей моделью УЗ и описывает ситуацию закупки продукции у внешнего поставщика, которая характеризуется следующими допущениями: интенсивность потребления является априорно известной и постоянной величиной; заказ доставляется со склада, на котором хранится ранее произведенный товар; время поставки заказа является известной и постоянной величиной; каждый заказ поставляется в виде одной партии; затраты на осуществление заказа не зависят от размера заказа; затраты на хранение запаса пропорциональны его размеру; отсутствие запаса (дефицит) является недопустимым.

Входные параметры модели Уилсона 1) ν – интенсивность (скорость) потребления запаса, [ед. тов. /ед. t]; 2) s – затраты на хранение запаса, [руб. / ед. тов. ⋅ ед. t ]; 3) K – затраты на осуществление заказа, включающие оформление и доставку заказа, [руб. ]; 4) t д – время доставки заказа, [ед. t]. 1) Q – размер заказа, [ед. тов. ]; 2) L – общие затраты на управление запасами в единицу времени, [руб. /ед. t]; 3) τ – период поставки, т. е. время между подачами заказа или между поставками, [ед. t]; 4) h 0 – точка заказа, т. е. размер запаса на складе, при котором надо подавать заказ на доставку очередной партии, [ед. тов. ]. Циклы изменения уровня запаса в модели Уилсона графически представлены на рис. Максимальное количество продукции, которая находится в запасе, совпадает с размером заказа Q.

Формулы модели Уилсона где Qw – оптимальный размер заказа в модели Уилсона Задача Объем продажи некоторого магазина составляет в год 500 упаковок супа в пакетах. Величина спроса равномерно распределяется в течение года. Цена покупки одного пакета равна 2 руб. За доставку заказа владелец магазина должен заплатить 10 руб. Время доставки заказа от поставщика составляет 12 рабочих дней (при 6 -дневной рабочей неделе). По оценкам специалистов, издержки хранения в год составляют 40 коп. за один пакет. Необходимо определить: сколько пакетов должен заказывать владелец магазина для одной поставки; частоту заказов; точку заказа. Известно, что магазин работает 300 дней в году.

Решение Примем за единицу времени год, тогда ν = 500 шт. пакетов в год, K =10 руб. , s = 0, 4 руб. /шт. ⋅ год. Поскольку пакеты супа заказываются со склада поставщика, а не производятся самостоятельно, то будем использовать модель Уилсона. Поскольку число пакетов должно быть целым, то будем заказывать по 158 штук. При расчете других параметров задачи будем использовать не Q* =158, 11, а Q=158. Годовые затраты на УЗ равны Подача каждого нового заказа должна производиться через Поскольку известно, что в данном случае год равен 300 рабочим дням, то Заказ следует подавать при уровне запаса равном т. е. эти 20 пакетов будут проданы в течение 12 дней, пока будет доставляться заказ.

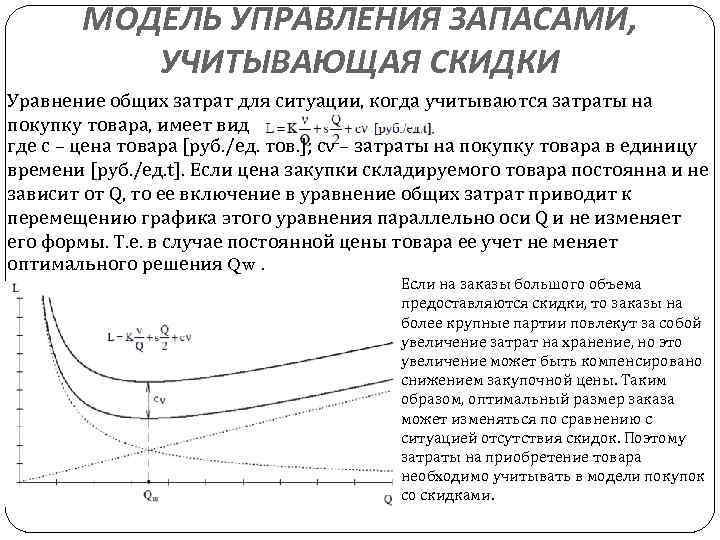МОДЕЛЬ УПРАВЛЕНИЯ ЗАПАСАМИ, УЧИТЫВАЮЩАЯ СКИДКИ Уравнение общих затрат для ситуации, когда учитываются затраты на покупку товара, имеет вид где с – цена товара [руб. /ед. тов. ]; сν – затраты на покупку товара в единицу времени [руб. /ед. t]. Если цена закупки складируемого товара постоянна и не зависит от Q, то ее включение в уравнение общих затрат приводит к перемещению графика этого уравнения параллельно оси Q и не изменяет его формы. Т. е. в случае постоянной цены товара ее учет не меняет оптимального решения Qw. Если на заказы большого объема предоставляются скидки, то заказы на более крупные партии повлекут за собой увеличение затрат на хранение, но это увеличение может быть компенсировано снижением закупочной цены. Таким образом, оптимальный размер заказа может изменяться по сравнению с ситуацией отсутствия скидок. Поэтому затраты на приобретение товара необходимо учитывать в модели покупок со скидками.

Новые входные параметры модели, учитывающей скидки 1) Qр1, Qр2 – точки разрыва цен, т. е. размеры покупок, при которых начинают действовать соответственно первая и вторая скидки, [ед. тов. ]; 2) с, с1, с2 – соответственно исходная цена, цена с первой скидкой, цена со второй скидкой, [руб. /ед. тов. ]. Влияние единственной скидки на общие затраты на УЗ показано на рис. Чтобы определить оптимальный размер заказа Q∗ , необходимо проанализировать, в какую из трех областей попадает точка разрыва цены Qр1. Правило выбора Q∗ для случая с одной скидкой имеет вид: Задача Пусть затраты на заказ равны 10 руб. , затраты на хранение продукции 1 руб. в сутки, интенсивность потребления товара 5 шт. в день, цена товара – 2 руб. за штуку, а при объеме закупки 15 шт. и более – 1 руб. Определите оптимальный размер заказа, цену покупки и затраты на УЗ.

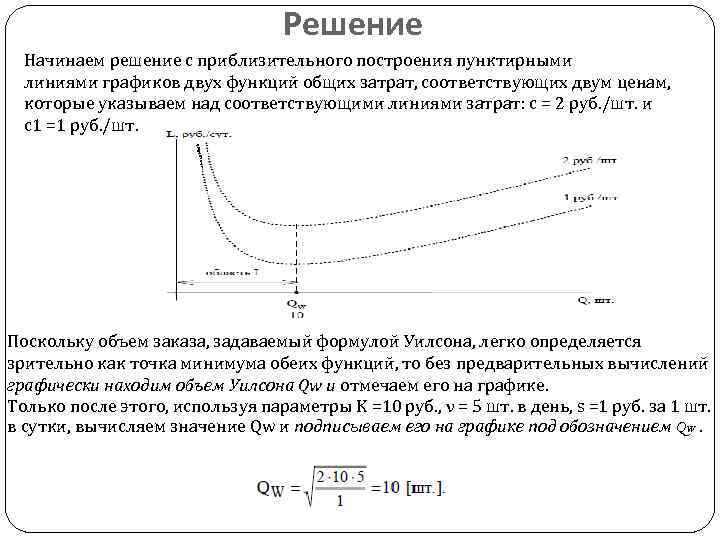Решение Начинаем решение с приблизительного построения пунктирными линиями графиков двух функций общих затрат, соответствующих двум ценам, которые указываем над соответствующими линиями затрат: с = 2 руб. /шт. и с1 =1 руб. /шт. Поскольку объем заказа, задаваемый формулой Уилсона, легко определяется зрительно как точка минимума обеих функций, то без предварительных вычислений графически находим объем Уилсона Qw и отмечаем его на графике. Только после этого, используя параметры K =10 руб. , ν = 5 шт. в день, s =1 руб. за 1 шт. в сутки, вычисляем значение Qw и подписываем его на графике под обозначением Qw.

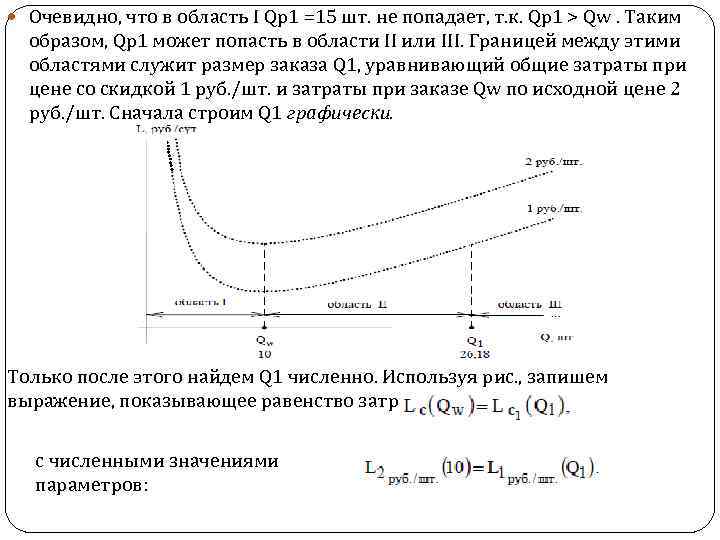Очевидно, что в область I Qр1 =15 шт. не попадает, т. к. Qр1 > Qw. Таким образом, Qр1 может попасть в области II или III. Границей между этими областями служит размер заказа Q 1, уравнивающий общие затраты при цене со скидкой 1 руб. /шт. и затраты при заказе Qw по исходной цене 2 руб. /шт. Сначала строим Q 1 графически. Только после этого найдем Q 1 численно. Используя рис. , запишем выражение, показывающее равенство затрат, с численными значениями параметров:

После раскрытия левой и правой части получаем Всегда выбираем больший из корней Q 1 = 26, 18, т. к. меньший по значению корень не дает нам информации о границе областей II и III, и отмечаем численное значение 26, 18 на графике. Таким образом, точка разрыва цен Qр1 =15 попадает в область II, т. к. 10 ≤ 15 ≤ 26, 18 (Q ≤ Qр1 ≤ Q 1). Отметим эту точку на графике в любом месте области II

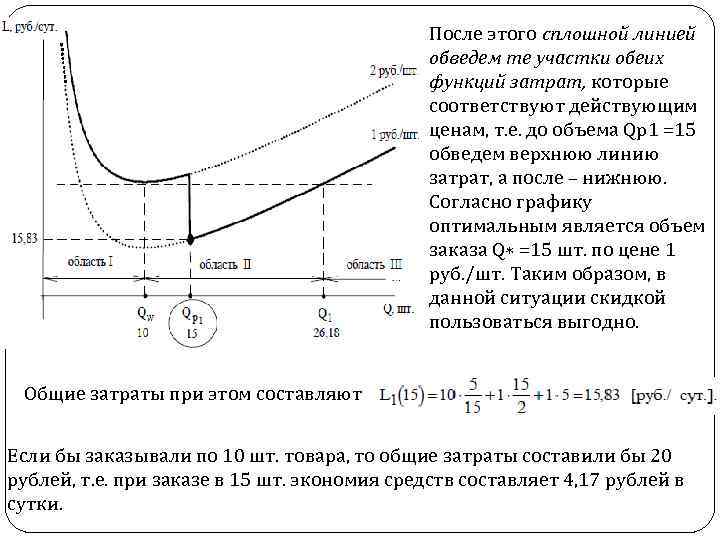После этого сплошной линией обведем те участки обеих функций затрат, которые соответствуют действующим ценам, т. е. до объема Qр1 =15 обведем верхнюю линию затрат, а после – нижнюю. Согласно графику оптимальным является объем заказа Q∗ =15 шт. по цене 1 руб. /шт. Таким образом, в данной ситуации скидкой пользоваться выгодно. Общие затраты при этом составляют Если бы заказывали по 10 шт. товара, то общие затраты составили бы 20 рублей, т. е. при заказе в 15 шт. экономия средств составляет 4, 17 рублей в сутки.

Производственная функция. Модель Кобба-Дугласа. Рассмотрим одну из наиболее распространенных производственных функций – функцию Кобба-Дугласа: Y = AKαLβ, где A, α, β > 0 – константы, α + β < 1; К – объем фондов либо в стоимостном выражении, либо в натуральном количестве, скажем, число станков; L – объем трудовых ресурсов, также в стоимостном выражении, либо в натуральном количестве – число рабочих, человеко-дней и т. п. и, наконец, Y – выпуск продукции в стоимостном или натуральном выражении. Проверим, выполняются ли требования к производственным функциям. Положительность предельных продуктов: ∂Y/∂K = AαKα-1 Lβ > 0, ∂Y/∂L = AβKαLβ-1 > 0. Отрицательность вторых частных производных, т. е. убывание предельных продуктов: ∂Y 2/∂K 2 = Aα(α– 1)Kα-2 Lβ < 0, ∂Y 2/∂L 2 = Aβ(β– 1)KαLβ-2> 0. Перейдем к основным экономико-математическим характеристикам производственной функции Кобба-Дугласа. Средняя производительность труда определяется как y = Y/L – отношение объема произведенного продукта к количеству затраченного труда; средняя фондоотдача k = Y/K – отношение объема произведенного продукта к величине фондов.

Для функции Кобба-Дугласа средняя производительность труда y = AKαLβ− 1, и в силу условия β < 1 является убывающей функцией L, т. е. с увеличением затрат труда средняя производительность труда падает. Этот вывод допускает естественное объяснение – поскольку величина второго фактора К остается неизменной, то, значит, вновь привлекаемая рабочая сила не обеспечивается дополнительными средствами производства, что и приводит к снижению производительности труда (это справедливо и в самом общем случае – на уровне производственных множеств). Предельная производительность труда ∂Y/∂L = AβKαLβ-1 > 0, откуда видно, что для функции Кобба-Дугласа предельная производительность труда пропорциональна средней производительности и меньше ее. Аналогично определяются средняя и предельная фондоотдачи. Для них так-же справедливо указанное соотношение – предельная фондоотдача пропорциональна средней фондоотдаче и меньше ее. Важное значение имеет такая характеристика, как фондовооруженность f = K/L, показывающая объем фондов, приходящийся на одного работника (на одну единицу труда). Найдем теперь эластичность продукции по труду: (∂Y/∂L): (Y/L) = (∂Y/∂L)L/Y = AβKαLβ-1 L/(AKαLβ) = β.

Таким образом, ясен смысл параметра β – это эластичность (отношение предельной производительности труда к средней производительности труда) продукции по труду. Эластичность продукции по труду означает, что для увеличения выпуска продукции на 1 % необходимо увеличить объем трудовых ресурсов на β %. Аналогичный смысл имеет параметр α – это эластичность продукции по фондам. И еще одно значение представляется интересным. Пусть α + β = 1. Легко проверить, что Y = (∂Y/∂K)/K + (∂Y/∂L)L (подставляя уже вычисленные ранее ∂Y/∂K, ∂Y/∂L в эту формулу). Будем считать, что общество состоит только из рабочих и предпринимателей. Тогда доход Y распадается на две части – доход рабочих и доход предпринимателей. Поскольку при оптимальном размере фирмы величина ∂Y/∂L – предельный продукт по труду – совпадает с заработной платой (это можно доказать), то (∂Y/∂L)L представляет собой доход рабочих. Аналогично величина ∂Y/∂K есть предельная фондоотдача, экономический смысл которой есть норма прибыли, следовательно, (∂Y/∂K)K представляет доход предпринимателей. Функция Кобба-Дугласа – наиболее известная среди всех производственных функций. На практике при ее построении иногда отказываются от некоторых требований (например, сумма α + β может быть больше 1 и т. п. ).

Задача Пусть производственная функция есть функция Кобба -Дугласа. Чтобы увеличить выпуск продукции на а = 3%, надо увеличить основные фонды на b = 6 % или численность работников на c = 9%. В настоящее время один работник за месяц производит продукции на М = 104 руб. , а всего работников L = 1000. Основные фонды оцениваются в K = 108 руб. Найти производственную функцию. Решение. Найдем коэффициенты α, β: α = а/b = 3/6 = 1/2, β = а/с = 3/9 = 1/3, следовательно, Y = AK 1/2 L 1/3. Для нахождения А подставим в эту формулу значения K, L, M, имея в виду, что Y = ML = 1000. 104 = 107 – 107 = А(108)1/210001/3. Отсюда А = 100. Таким образом, производственная функция имеет вид: Y = 100 K 1/2 L 1/3.

Модель межотраслевого баланса Леонтьева Межотраслевой баланс в экономике – это метод анализа взаимосвязей между различными секторами экономической системы. Предположим, что исследуемую экономическую систему можно разделить на несколько отраслей (секторов), производящих определенные товары и услуги (например: сельское хозяйство, промышленность, транспорт, энергетика и т. п. ). При производстве товаров и услуг в каждом секторе расходуются ресурсы в виде сырья, рабочей силы, оборудования и др. , которые производятся как в других секторах хозяйства, так и в данном секторе. Это означает, что каждый сектор экономики выступает в системе межотраслевых связей одновременно производителем и потребителем. Цель балансового анализа – определить, сколько продукции должен произвести каждый сектор для того, чтобы удовлетворить все потребности экономической системы в его продукции. Рассмотрим упрощенную модель межотраслевого баланса – баланс экономики, состоящей из трех отраслей – сельского хозяйства, промышленности и домашних хозяйств. В качестве единицы измерения объемов товаров и услуг каждого сектора выберем их стоимость. Предположим, что вся продукция сельского хозяйства составляет 200 денежных единиц, из них 50 единиц потребляется внутри самой отрасли, 40 единиц – в промышленности и 110 единиц – в домашних хозяйствах. Продукция промышленности составляет 250 единиц, из них 70 единиц потребляются в сельском хозяйстве, 30 единиц – в промышленности и 150 – в домашних хозяйствах. Домашние хозяйства производят 300 единиц продукции, из них 80 единиц потребляются в сельском хозяйстве, 180 – в промышленности и 40 – внутри самого сектора. Эти данные можно свести в таблицу межотраслевого баланса.

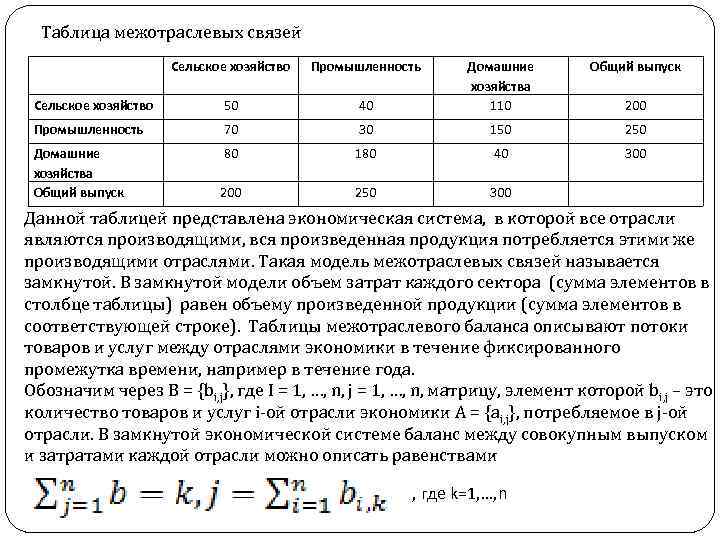Таблица межотраслевых связей Сельское хозяйство Промышленность Общий выпуск 40 Домашние хозяйства 110 Сельское хозяйство 50 Промышленность 70 30 150 250 Домашние хозяйства Общий выпуск 80 180 40 300 250 300 200 Данной таблицей представлена экономическая система, в которой все отрасли являются производящими, вся произведенная продукция потребляется этими же производящими отраслями. Такая модель межотраслевых связей называется замкнутой. В замкнутой модели объем затрат каждого сектора (сумма элементов в столбце таблицы) равен объему произведенной продукции (сумма элементов в соответствующей строке). Таблицы межотраслевого баланса описывают потоки товаров и услуг между отраслями экономики в течение фиксированного промежутка времени, например в течение года. Обозначим через B = {bi, j}, где I = 1, …, n, j = 1, …, n, матрицу, элемент которой bi, j – это количество товаров и услуг i-ой отрасли экономики А = {аi, j}, потребляемое в j-ой отрасли. В замкнутой экономической системе баланс между совокупным выпуском и затратами каждой отрасли можно описать равенствами , где k=1, …, n

Матрица В называется матрицей межотраслевого баланса, или матрицей Леонтьева. Рассмотрим открытую систему межотраслевых связей, в которой вся произведенная продукция (совокупный продукт) разделяется на две части: одна часть продукции (промежуточный продукт) идет на потребление в производящих секторах, а другая часть (конечный продукт) потребляется вне сферы материального производства – в секторе конечного спроса. Обозначим: xj – объем выпуска i-й отрасли; bi, j – объем продукции i-ой отрасли, потребляемой в j-ой отрасли; ci – конечный продукт, т. е. объем потребления продукции i-ой отрасли в непроизводственной сфере; ai, j = bi, j/xj - количество продукции i-ой отрасли, которое расходуется на производство одной единицы продукции j-ой отрасли. Числа ai, j называются коэффициентами прямых затрат j-ой отрасли и характеризуют технологию этой отрасли. Межотраслевой баланс – это равенство объема выпуска каждой производящей отрасли суммарному объему ее продукции, потребляемой производственными отраслями и отраслью конечного спроса. Последние равенства описывают технологию производства и структуру экономических связей и означают, что в отрасль конечного спроса поступает та часть произведенной продукции, которая осталась после того, как обеспечены потребности производящих отраслей. Для дальнейшего рассмотрения модели Леонтьева сделаем два важных предположения:

1. Сложившуюся технологию производства считаем неизменной, таким образом матрица А = {аi, j} постоянна. 2. Для выпуска j-ой отраслью продукции объема хj надо ресурсов в количестве. Xi∑iai, j. Это требование означает, что каждая отрасль способна произвести любой объем своей продукции, при условии, что ей будут обеспечены ресурсы в необходимом количестве. На самом деле это не так, ибо производственные возможности каждой отрасли ограничены имеющимся объемом трудовых ресурсов и основных фондов. Пусть Х = {xi} – вектор объемов производства в отраслях, тогда А. Х – потребляемые объемы продукции этих отраслей, таким образом, внепроизводственной сферы – на потребление остается только Х – А*Х. Назовем экономику высокоэффективной, если А*Х ≤ С, т. е. в производственной сфере тратится меньше, чем в сфере потребления.

Общие модели развития экономики. Модель Солоу – одна из моделей экономического роста, в которой при некоторых заданных упрощенных условиях формируется результативное уравнение, задающее равновесную траекторию роста при полной занятости. Модель позволяет рассчитать темп прироста занятости, при которой достигается устойчивое равновесие. Используется линейная однородная производственная функция: Y = F (K, L), где L–единица труда, K–капитал (в у. е. ). Предельная склонность к сбережению (%) – ᴪ Темп прироста трудовых ресурсов (%)

Задача Производство НД отображается в производственной функции (ПФ): Y= занятость трудовой экономический солоу В период t в хозяйстве было L единиц труда и K капитала. Темп прироста трудовых ресурсов равен за период. В каком направлении будет изменяться темп прироста НД в соответствии с моделью экономического роста Солоу? Какой объем капитала обеспечит в исходных условиях равновесный рост с периода t 1? Исходные данные: L = 9; K 0 = 570; ᴪ = 41; = 3. Решение. Для ответа на 1 вопрос определим темп роста при исходных экономических параметрах и сравним его с равновесным темпом роста в указанной модели. В модели Солоу динамическое равновесие устанавливается тогда, когда темпы роста НД и труда совпадают, следовательно, в условиях задачи равновесный темп роста равен: 1/k=100/3, следовательно, k=0. 03, ᴪ = 1+0. 03 = 1. 03.

В исходном периоде найдем Y 0 = В периоде t 1 определим прирост трудовых ресурсов: Исходя из полученных данных, получим: Найдем темп роста: = Ответ на 2 вопрос выводится из условия равновесного роста: Так как Y=K*0. 07 и Y= , то можно приравнять данные уравнения и найти K: K*0. 07 = , следовательно, K = 1836. 7 у. е. Вывод: таким образом, темп роста движется в сторону уменьшения и приближается к значению 1, 04; полученный объем капитала (1836. 7 у. е. ) при неизменных условиях обеспечит равновесный рост.

Модель равновесия Курно Данная модель была предложена французским математиком А. О. Курно исходил из того, что: обе фирмы производят однородный товар; им известна кривая рыночного спроса; обе фирмы принимают решения о производстве одновременно, причем самостоятельно и независимо друг от друга; каждая из фирм предполагает выпуск конкурента постоянным; продавцы не могут иметь точной информации о своих ошибках относительно выбранных объемов производства. Рассмотрим данную модель с помощью кривых реагирования. Кривые реагирования показывают максимизирующие прибыль размеры выпуска, который будет осуществляться одной фирмой, если даны объемы выпуска фирмы-соперницы. Если бы фирма А выпускала 30 ед. , то выпуск фирмой Б был бы равен нулю. Если бы QБ = 30, то QА = 0. Фирма А начинает производство первой. До того как фирма Б начнет производство, фирма А обладает всем рынком и чувствует себя монополистом, выбирая объем производства 15 единиц, максимизирующий его прибыль. Затем на рынке появляется фирма Б, предполагая, что фирма А не будет отвечать изменением выпуска. Фирма Б сможет обслужить всех тех покупателей, которые купили бы продукцию, если бы цена упала ниже текущей цены фирмы А. В этом случае объем выпуска фирмы Б составит 7, 5 единиц. Падение цены товара, вызванное дополнительным производством фирмы Б, приводит к изменению кривой спроса фирмы А. Теперь уже А предполагает, что Б будет производить 7, 5 единиц продукции. Она отрегулирует свой выпуск до 11, 25 единиц.

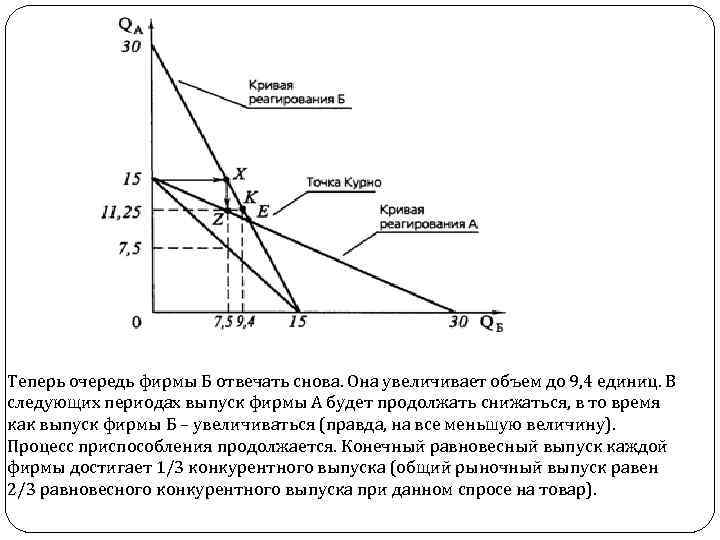Теперь очередь фирмы Б отвечать снова. Она увеличивает объем до 9, 4 единиц. В следующих периодах выпуск фирмы А будет продолжать снижаться, в то время как выпуск фирмы Б – увеличиваться (правда, на все меньшую величину). Процесс приспособления продолжается. Конечный равновесный выпуск каждой фирмы достигает 1/3 конкурентного выпуска (общий рыночный выпуск равен 2/3 равновесного конкурентного выпуска при данном спросе на товар).

Пересечение кривых реагирования двух фирм – точка Е – показывает равновесие Курно: каждая фирма правильно угадывает поведение конкурента и принимает самое оптимальное для себя решение. При равновесии Курно каждый дуополист устанавливает объем производства, который максимизирует его прибыль при данном объеме производства своего конкурента, и поэтому ни у одного дуополиста нет стимула менять свой объем производства. Модель равновесия Курно предполагает, что фирмы - дуополисты конкурируют друг с другом. Ситуация принципиально изменится, если дуополисты достигнут соглашения и будут коллективно намечать объем производства таким образом, чтобы максимизировать совокупную прибыль, а затем разделить ее пополам. Тогда множество возможных решений придется на контрактную линию. И если они будут делить прибыль пополам, то и будут производить каждую половину продукции (в нашем примере по 7, 5 единиц). Сравнение показывает, что при равновесии Курно общий объем производства выше, чем при дуополистическом сговоре (20 > 15), но ниже, чем он был бы при конкурентном равновесии (20 < 30).

Задача потребительского выбора. Уравнение Слуцкого. Одним из основных в теории потребительского выбора является уравнение Слуцкого, опубликованное российским математиком Е. Е. Слуцким в 1915 году: Это уравнение позволяет увязать действие эффекта замены и эф фекта дохода с результирующим изменением спроса. Первое слагаемое в правой части описывает действие эффекта замены, второе – действие эффекта дохода, выраженное в тех же единицах измерения (множитель хj приводит их к одной размерности). Слева записано результирующее воздействие на спрос, складывающееся из изменения структуры спроса и общего изменения при изменении уровня реального дохода. Для ценных товаров величина ((xi )`I ) > 0 , т. е. спрос растет при росте дохода. В этом случае, согласно уравнению Слуцкого, ((xi)`pj )<((xi)`pj )comp: если спрос растет, то он растет больше при наличии компенсации, если спрос падает то в меньшей степени. Может оказаться и так, что ((xi)`pj )<0, но ((xi)`pj )comp>0, то есть товары i и j взаимозаменяемы, но представляются взаимодополняемыми без учета компенсации. Уравнение Слуцкого может рассматриваться как при разных, так и при совпадающих i и j.

Из свойств функции полезности потребителя вытекает, что ((xi)`pj )comp<0 (спрос на товар растет при росте цены – такие товары называются товарами Гиффина), то отсюда вытекает, что ((xi)`I)<0 – то есть это обязательно малоценный (худший) товар. Обычно приводимый в качестве примера товара Гиффина картофель удовлетворяет этому условию, в то же время золото, например, не может ему удовлетворять. Таким образом, рост спроса на золото при росте его цены, наблюдавшийся одно время в СССР, нужно объяснить другими причинами, – главным образом, скрытой инфляцией и узостью сферы вложения свободных средств населения в тот период. В качестве иллюстрации покажем, что если в задаче потребительского выбора всего два товара, то они обязательно являются взаимозаменяемыми. Для этого воспользуемся тем, что ((xi)`pj )comp<0, и положительностью частных производных функции полезности. Предположим, что выросла цена 1 -го товара р1. Поскольку ((xi)`pj )comp<0 спрос на этот товар при условии компенсации падает. Если бы при этом упал спрос и на второй товар, то мы получили бы точку, в которой обоих товаров меньше, чем в начальной. Следовательно, в этой точке значение функции полезности u(х1, x 2) должно быть также меньше (а мы знаем, что в условиях компенсации оно равно начальному). Следовательно, спрос на второй товар при условии компенсации должен вырасти (т. е. ((x 2 )`p 1 ) comp > 0 и он является взаимозаменяемым с первым товаром.