Э К О Н О М Е Т

Э К О Н О М Е Т Р И К А

Тема 2. Корреляция. Парная регрессия. 1. Функциональные и корреляционные типы связей. Ковариация, корреляция. 2. Анализ линейной статистической связи экономических данных, корреляция; вычисление коэффициентов корреляции, проверка значимости. 3. Измерение тесноты связи между показателями. Анализ матрицы коэффициентов парной корреляции. 4. Понятия регрессионного анализа: зависимые и независимые переменные. 5. Предпосылки применения метода наименьших квадратов (МНК). 6. Свойства оценок метода наименьших квадратов (МНК). 7. Линейная модель парной регрессии. Оценка параметров модели с помощью метода наименьших квадратов (МНК). 8. Показатели качества регрессии модели парной регрессии. 9. Анализ статистической значимости параметров модели парной регрессии. 10. Интервальная оценка параметров модели парной регрессии. 11. Проверка выполнения предпосылок МНК. 12. Интервалы прогноза по линейному уравнению парной регрессии. (Прогнозирование с применением уравнения регрессии). 13. Понятие и причины гетероскедастичности. Последствия гетероскедастичности. Обнаружение гетероскедастичности. 14. Нелинейная регрессия. Нелинейные модели и их линеаризация.

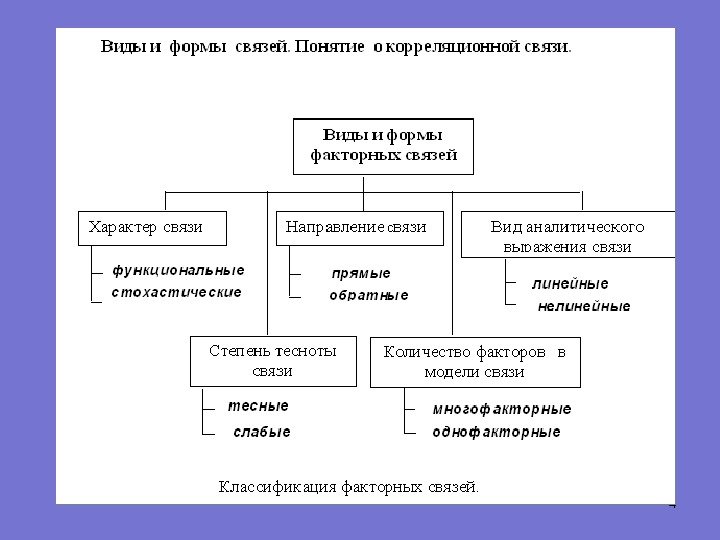
Функциональные и корреляционные типы связей Рассматривая зависимости между признаками, выделяют две категории зависимости: 1) функциональные и 2) корреляционные. Зависимость величины Y от Х называется функциональной , если каждому значению величины Х соответствует единственное значение величины У. Корреляционная связь — это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных.

Корреляция Основная задача корреляционного анализа заключается в выявлении взаимосвязи между случайными переменными путем точечной и интервальной оценки парных (частных) коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации. Кроме того, с помощью корреляционного анализа решаются следующие задачи: • отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связи между ними; • обнаружение ранее неизвестных причинных связей.

6 • При изучении взаимосвязи между двумя факторами их, как правило, обозначают X и Y • Для измерения силы связи между двумя переменными используется статистическая характеристика, называемая • коэффициентом корреляции 1 1 , 2 2 1 1 ( )( ) ( ) n n i i i x y n n x y i i 1 x x y y n 1 r S S x x y y

Оценка значимости коэффициента корреляции 7 при малых объемах выборки выполняется с использованием t — критерия Стьюдента. Вычисленное по этой формуле значение t набл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n-2). Если t набл > t кр , то полученное значение коэффициента корре ляции признается значимым. При этом фактическое (наблюдаемое) значение этого критерия определяется по формуле:

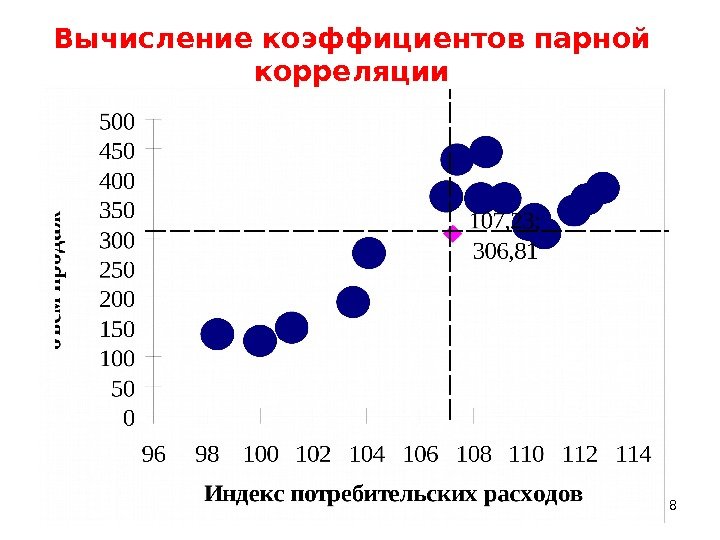
Вычисление коэффициентов парной корреляции

Вычисление коэффициентов парной корреляции

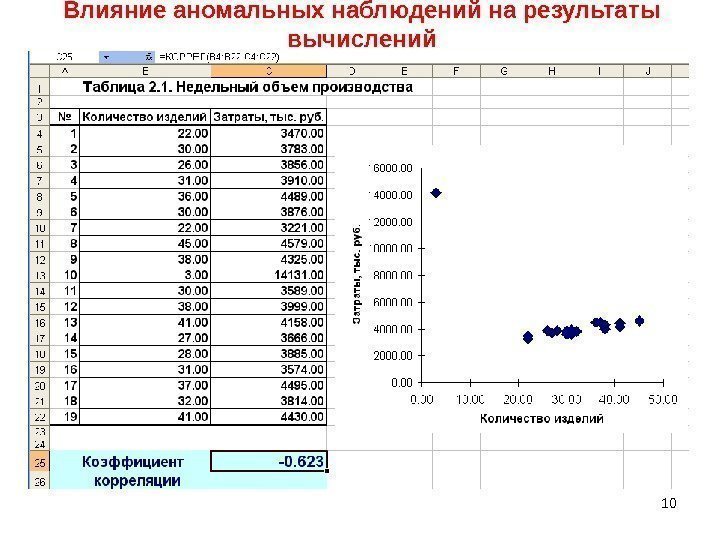
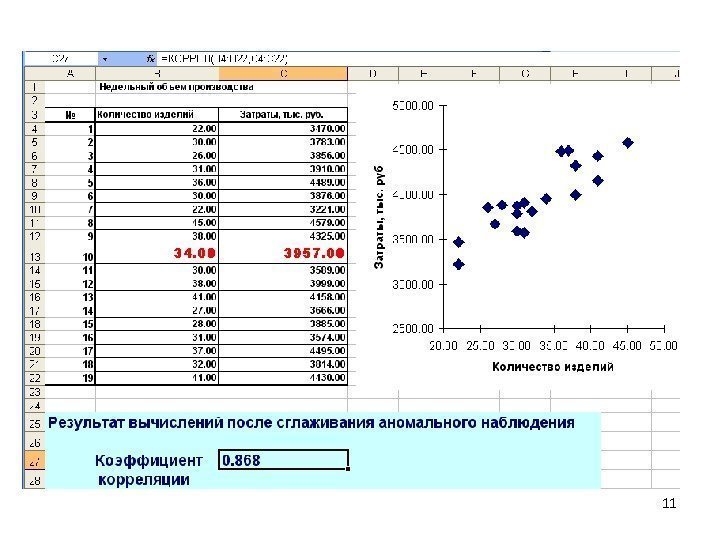
Влияние аномальных наблюдений на результаты вычислений

Матрица коэффициентов парной корреляции • Коэффициенты парной корреляции используются для измерения силы линейных связей различных пар признаков из их множества. Для множества признаков получают матрицу коэффициентов парной корреляции R.

Задача 1. Задание по эконометрическому моделированию стоимости квартир в Московской области 1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции. 2. Постройте поле корреляции результативного признака и наиболее тесно связанного с ним фактора. 3. Рассчитайте параметры линейной парной регрессии. 4. Оцените качество каждой модели через коэффициент детерминации, среднюю ошибку аппроксимации и F-критерий Фишера. 5. Осуществите прогнозирование среднего значения показателя при уровне значимости , если прогнозное значения фактора составит 80% от его максимального значения. Представьте графически: фактические и модельные значения, точки прогноза. 6. Используя пошаговую множественную регрессию (метод исключения или метод включения), постройте модель формирования цены квартиры за счёт значимых факторов. Дайте экономическую интерпретацию коэффициентов модели регрессии. 7. Оцените качество построенной модели. Улучшилось ли качество модели по сравнению с однофакторной моделью? Дайте оценку влияния значимых факторов на результат с помощью коэффициентов эластичности, — и — коэффициентов. •

14 Регрессионный анализ • предназначен для исследования зависимости исследуемой переменной от различных факторов и отображения их взаимосвязи в форме регрессионной модели. • В регрессионных моделях зависимая переменная Y может быть представлена в виде функции f (Х), где — Х 1, Х 2, …, Х m независимые (объясняющие) переменные, или факторы. • Связь между переменной Y и m независимыми факторами Х можно охарактеризовать функцией регрессии Y= f ( Х 1, Х 2, …, Х m ), которая показывает, каково будет в среднем значение переменной yi, если переменные X i примут конкретные значения.

15 Примеры задач , решаемых с помощью регрессионных моделей • Исследование зависимости заработной платы ( Y ) от возраста ( X 1 ), уровня образования ( X 2 ), пола ( X 3 ), стажа работы ( X 4 ) ( ) • Прогноз и планирование выпускаемой продукции по факторам производства (производственная функция Кобба – Дугласа означает, что объем выпуска продукции ( Y) , является функцией количества капитала ( K ) и количества ( L ) труда ). • Прогноз объемов потребления продукции или услуг определенного вида (кривая Энгеля где Y — удельная величина спроса, Х — среднедушевой доход). 1 2 0 a a y a K L 0 1 1 2 2 3 3 4 4 y a a x a x 2 0 11 a x a y a e

16 Регрессионные модели с переменной структурой (фиктивные переменные). • Построена регрессионная модель зависимости заработной платы работника (Y) от возраста (Х) с использованием фиктивной переменной по фактору пол по 20 работникам одного предприятия • Из полученного уравнения регрессии следует, что при одном и том же возрасте заработная плата у работников мужчин на 17, 27$ в месяц выше, чем у женщин. • Из модели, включающей фиктивную переменную можно получить частные уравнения регрессии для работников мужчин ( z =1) и женщин ( z =0): 60, 71 6, 98 17, 27 y x z 77, 98 6, 98 ( 1) 60, 71 6, 98 ( 0). y x z

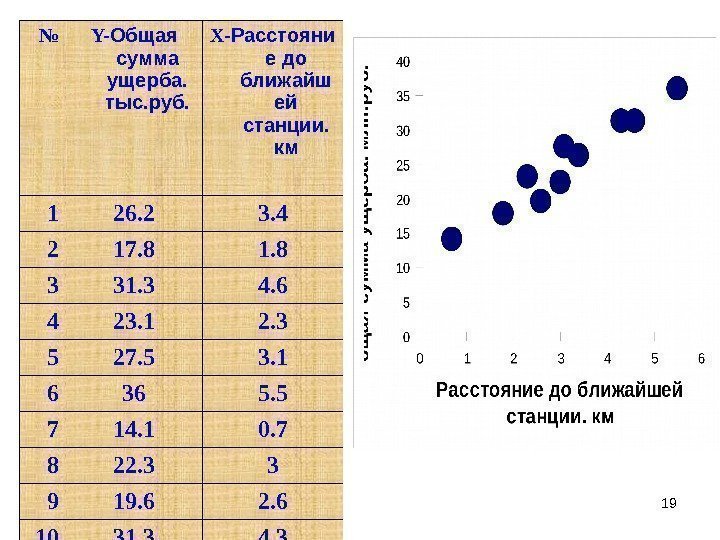
18 Администрация страховой компании приняла решение о введении нового вида услуг – страхование на случай пожара. С целью определения тарифов по выборке из 10 случаев пожаров анализируется зависимость стоимости ущерба, нанесенного пожаром от расстояния до ближайшей пожарной станции.

19 № Y- Общая сумма ущерба. тыс. руб. X- Расстояни е до ближайш ей станции. км 1 26. 2 3. 4 2 17. 8 1. 8 3 31. 3 4. 6 4 23. 1 2. 3 5 27. 5 3. 1 6 36 5. 5 7 14. 1 0. 7 8 22. 3 3 9 19. 6 2. 6 10 31. 3 4.

20 Прогноз по модели Y=10, 25+4, 69 X Прогноз Х По исходным данным полагают, что расстояние до ближайшей пожарной станции уменьшится на 5% от своего среднего уровня 3. 13 xкм прогноз 3. 13 0. 95 2. 97 xкм Прогноз Y прогноз 10. 25 4. 69 2. 97 24. 2. . y a b xтыс руб )

21 Построение доверительного интервала прогноза ˆ 1 0, 026 1, 801 1, 86 1 3, 51 10 17, 881 2 про гн о з с р α y n 2 i с р i=1(x — х ) U =S ×t × 1+1/n + (x — x ) Стандартная ошибка 1. 801( 0, 1; 8)1, 86 t

22 Построение доверительного интервала прогноза Строим доверительный интервал прогноза ущерба с вероятностью 0, 90 ( t=1, 86 ). Из полученных результатов видно, что интервал от 20, 67 до 27, 7 тыс. руб. ожидаемой величины ущерба довольно широкий. Значительная неопределенность прогноза линии регрессии, связана, прежде всего с малым объемом выборки ( n =10) , а также тем, что по мере удаления прогнозного знаения Х от среднего ширина доверительного интервала увеличивается. ˆ 1 0, 026 1, 801 1, 86 1 3, 51 10 17, 881 2 про гн о з с р α y n 2 i с р i=1(x — х ) U =S ×t × 1+1/n + (x — x ) Стандартная ошибка 1.

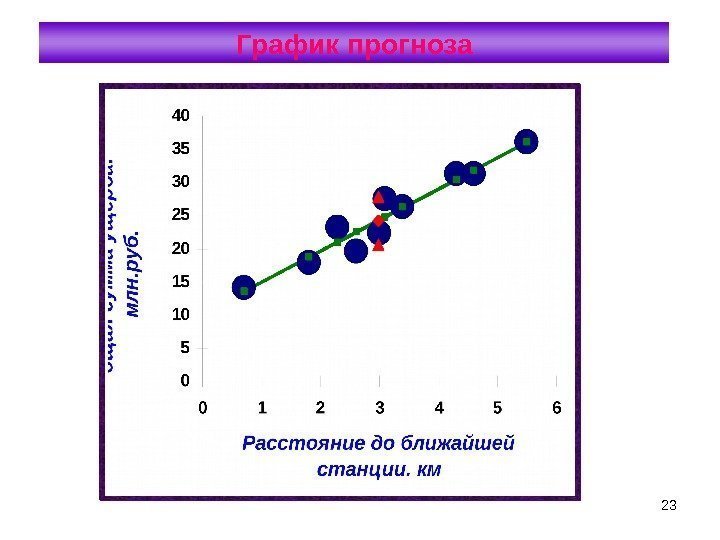
23 График прогноза