Донецкая общеобразовательная школа І – ІІІ ступеней №

Донецкая общеобразовательная школа І – ІІІ ступеней № 77 ЭТИ ОБЫКНОВЕННЫЕ – НЕОБЫКНОВЕННЫЕ ДРОБИ Урок обобщения знаний и умений 6 класс 2013 – 2014 учебный год

МАТЕМАТИКА и в шутку, и в серьёз для учеников 6-А класса и всех, кто интересуется математикой, для тех, кто в свободное от уроков время с удовольствием решает нестандартные задачи, кто ищет ответы на сложные вопросы по математике и не только по математике… Добрый день. Давайте знакомиться: я-Кот Учёный, который у Лукоморья бродил и вот к Вам на огонёк угодил. Вообще то, люди давно меня пытались приручить. Им, как Вам известно, удалось это лишь отчасти, то есть не совсем, не полностью. Вот и предлагаю Вам сегодня поговорить о ЧАСТЯХ ЦЕЛОГО. Люди называют их, эти части целого, ДРОБНЫМИ ЧИСЛАМИ.

В мире дробных чисел. С возникновением представлений о целых числах возникали представления и о частях единицы, точнее, о частях целого конкретного предмета. Исторически дроби возникли в процессе измерения. Дроби естественно появились при решении задач о разделе имущества, измерении земельных участков, исчислении времени и т.п. Дроби встречаются уже в самых древних дошедших до нас письменных источниках – вавилонских глиняных табличках и египетских папирусах. Шестидесятиричные дроби используются и поныне в делении углового и дугового градуса (а также часа) на 60 минут и минуты на 60 секунд. 35◦ 90◦ Более мелкой единице меры, как следствие раздробления, давали индивидуальные названия, и величины измеряли уже этой более мелкой единицей. В Древнем Риме была интересная система дробей. Она основывалась на делении древнеримской единицы массы – асса. Асс делили на12 равных частей. Двенадцатую часть асса называли унцией…
Чтобы познание дробей было процессом интересным, предлагаю работать в командах. Пусть каждая команда придумает себе название и девиз, который будет команду вдохновлять. Я же уверен, что победит сильнейший! Этого я желаю каждой команде. Ну, что, готовы? Тогда начнём с разминки: Когда делимое и частное равны между собой? Какое число делится на все числа без остатка? На озере росли лилии. Ежедневно число их удваивалось, и на 20-й день всё озеро заросло. На какой день заросло половина озера? О чём идёт речь: - она бывает барабанная или… пальцами; - бывает охотничья; - а ещё её учат в школе.. 1. 2. 3. 4. Замечательно! Теперь каждая команда будет идти к победе самостоятельно…

Эти обыкновенные - необыкновенные дроби… Знаете ли Вы, сколько это: четь, полчети, полполчети; полвторы; полпяты; полшесты?… А сколько это: седмина; пятина; полтина?... Почему некоторые части целого можно записать и обыкновенной, и десятичной дробью, а вот некоторые части целого возможно представить лишь обыкновенной дробью? (Приведите примеры таких дробей)

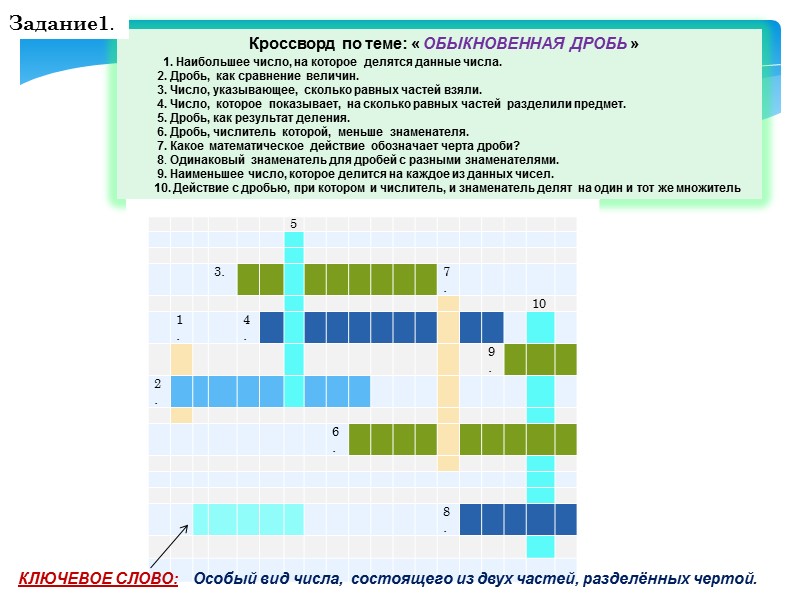
Кроссворд по теме: « ОБЫКНОВЕННАЯ ДРОБЬ » 1. Наибольшее число, на которое делятся данные числа. 2. Дробь, как сравнение величин. 3. Число, указывающее, сколько равных частей взяли. 4. Число, которое показывает, на сколько равных частей разделили предмет. 5. Дробь, как результат деления. 6. Дробь, числитель которой, меньше знаменателя. 7. Какое математическое действие обозначает черта дроби? 8. Одинаковый знаменатель для дробей с разными знаменателями. 9. Наименьшее число, которое делится на каждое из данных чисел. 10. Действие с дробью, при котором и числитель, и знаменатель делят на один и тот же множитель Задание1. КЛЮЧЕВОЕ СЛОВО: Особый вид числа, состоящего из двух частей, разделённых чертой.
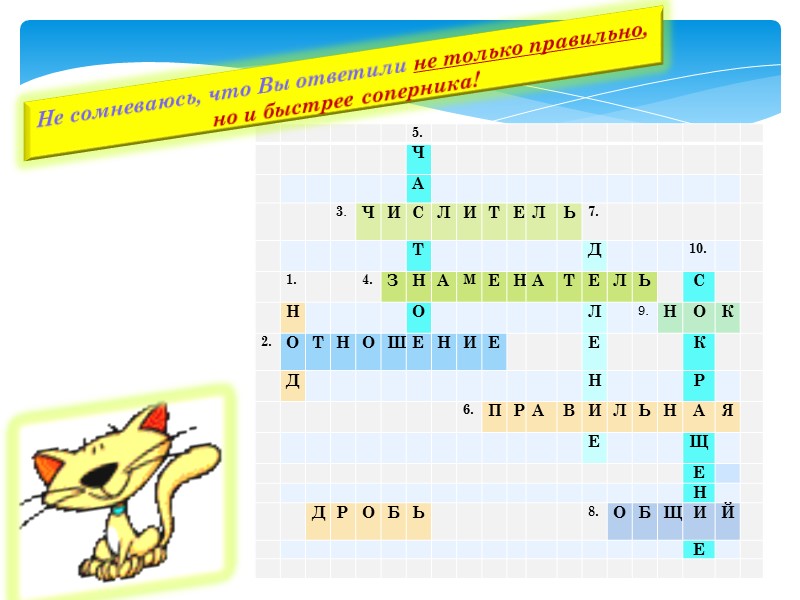
Не сомневаюсь, что Вы ответили не только правильно, но и быстрее соперника!
СТАРИННЫЕ названия дробей:
А знаете ли Вы, что древние египтяне изначально рассматривали дроби, числители которых были равны 1? Других дробей они просто не признавали! Попробуйте решить задачу, которую очень оригинально, на мой взгляд, решили древние египтяне, хотя для них это была единственная возможность её решения: « Следует поровну разделить между восьмью людьми семь хлебов.» Математическое решение этой задачи такое: 1 2 + 1 4 + 1 8 = 7 8 Согласитесь, это не только оригинально, но и практично: всего 3 кусочка, при этом один из них равен пол хлеба! И ничего, что другие поменьше… ЗАДАНИЕ 2
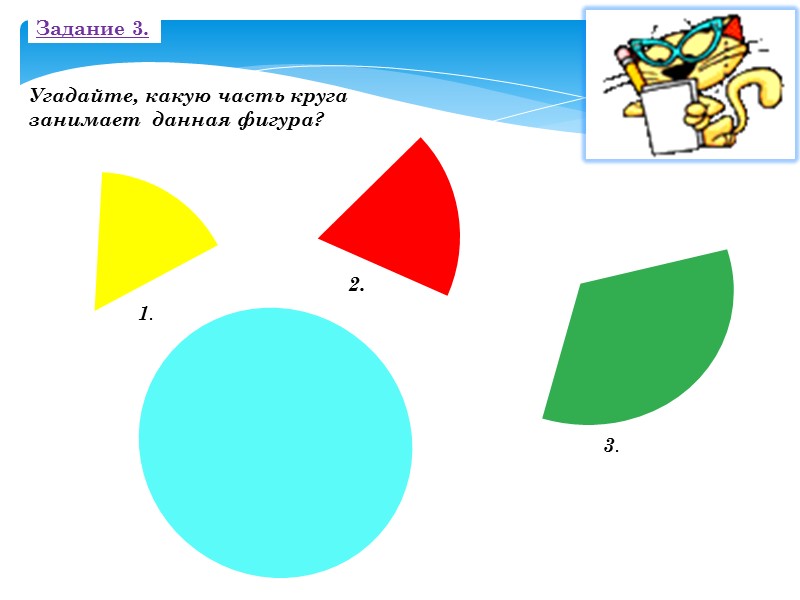
Задание 3. 2. 3. Угадайте, какую часть круга занимает данная фигура? 1.

Подумай и ответь: ЗАДАНИЕ 4 Запишите числами: Без четверти три - часа минут Половина девятого - часов минут. 3. Четверть двенадцатого - часов минут.

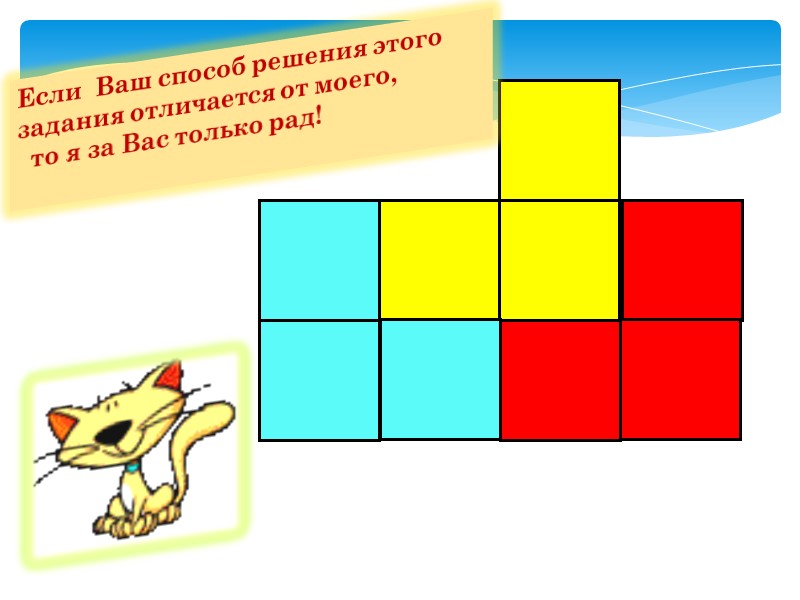
ЗАДАНИЕ 5 Разрежьте на три равные части фигуру: Подумай и ответь:

Если Ваш способ решения этого задания отличается от моего, то я за Вас только рад!

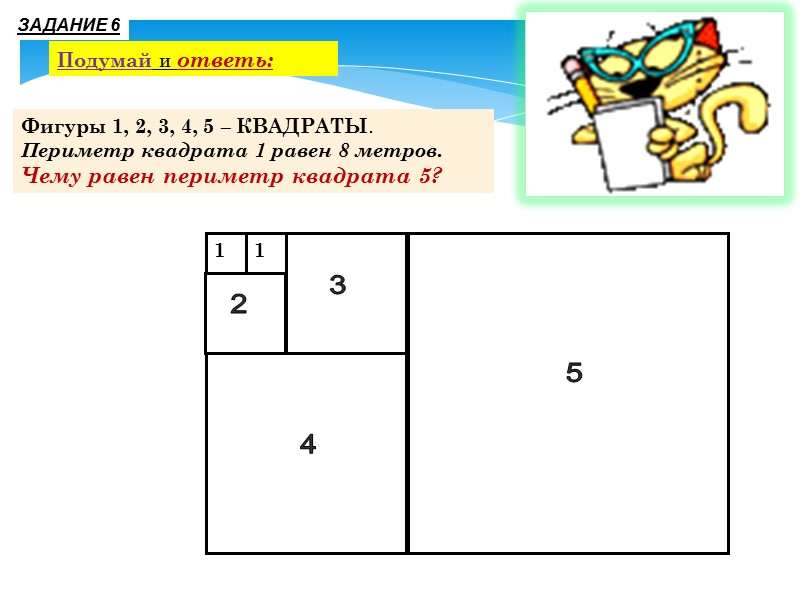
1 1 2 3 4 5 ЗАДАНИЕ 6 Подумай и ответь: Фигуры 1, 2, 3, 4, 5 – КВАДРАТЫ. Периметр квадрата 1 равен 8 метров. Чему равен периметр квадрата 5?

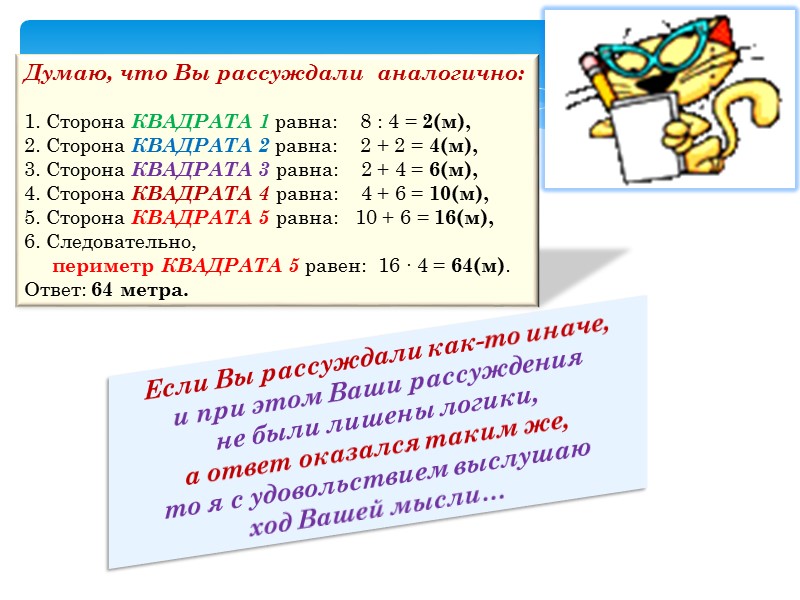
Думаю, что Вы рассуждали аналогично: 1. Сторона КВАДРАТА 1 равна: 8 : 4 = 2(м), 2. Сторона КВАДРАТА 2 равна: 2 + 2 = 4(м), 3. Сторона КВАДРАТА 3 равна: 2 + 4 = 6(м), 4. Сторона КВАДРАТА 4 равна: 4 + 6 = 10(м), 5. Сторона КВАДРАТА 5 равна: 10 + 6 = 16(м), 6. Следовательно, периметр КВАДРАТА 5 равен: 16 ∙ 4 = 64(м). Ответ: 64 метра. Если Вы рассуждали как-то иначе, и при этом Ваши рассуждения не были лишены логики, а ответ оказался таким же, то я с удовольствием выслушаю ход Вашей мысли…

«Человек подобен дроби, числитель которой есть то, что он есть на самом деле, а знаменатель есть то, что он о себе думает…» Задумайся над афоризмом: Пока Вы размышляете над афоризмом, и выбираете для себя - КАКИМ БЫТЬ, жюри подготовит результаты сегодняшнего соревнования. Я с Вами не прощаюсь, ведь впереди Вас ждут новые математические открытия, а значит, ДО НОВЫХ ВСТРЕЧ!

Думаю, что не только математические истины стали тебе сегодня понятны. Меня, КОТА УЧЁНОГО, ты больше узнаешь, если заглянешь в книги по истории…

Да, и вот ещё что: команды, на память о сегодняшней встрече обменяйтесь аппликациями, изготовленными из ЧАСТЕЙ фигур. Если проявите фантазию и старание, то ваши сувениры будут замечательными! Теперь всё. До свидания!

Эту познавательную встречу подготовили и провели ученики 6-А класса Донецкой общеобразовательной школы № 77: и их учитель математики Галина Степановна Люба Голеняева Диана Жолоб Станислав Козлов

Выражаем искреннюю благодарность Олесе Александровне, управлявшей компьютерной техникой во время проведения математического состязания, которая, являясь учителем биологии, на своих уроках не только привила нам любовь к преподаваемому предмету, но и сама была для нас образцом для подражания.
«В учении нельзя останавливаться» А ведь верно! Новые знания расширяют кругозор, дают возможность приблизиться к познанию законов природы, а значит, быть причастным к прогрессу в любой отрасли человеческой деятельности. Удачи всем, кто учится для того, чтобы многое знать и уметь! Удачи всем, кто учится для того, чтобы многое знать и уметь!

163-prezentaciya_obyknov._dr._1.pptx
- Количество слайдов: 23
