Дмитриев М.Г. «Теория принятия решений» Курс лекций Введение

Дмитриев М.Г. «Теория принятия решений» Курс лекций

Введение в теорию принятия решений 2 Введение в теорию принятия решений Теория принятия решений - это наука о выборе рациональных, оптимальных решений из множества допустимых, здесь изучаются способы поиска таких решений. Сегодня под теорией принятия решений понимают комплекс научных дисциплин, среди которых:

Введение в теорию принятия решений 3 Линейное программирование; Динамическое программирование; Целочисленное программирование; Нелинейное программирование; Булево программирование. (Перечисленные выше дисциплины относятся к дисциплине математическое программирование.) Векторная оптимизация (принятие решений в многокритериальной среде); Исследование операций; Теория игр; Системный анализ

Линейное программирование 4 Линейное программирование Линейное программирование (ЛП) – один из разделов математики, связанный с оптимизацией линейной функции на многогранниках. Имеет мощнейшее приложение, в частности, в экономике, для которой и создано. У истоков ЛП стоят такие ученые, как Л.В. Канторович (разработал метод потенциалов и двойственных оценок; в 1939 г. в Ленинграде написал первую книгу по ЛП), Т.Купманс (независимо от Канторовича Л.В. во время 2-й мировой войны сформулировал транспортную модель ЛП и разработал методы ее решения).

Линейное программирование 5 В 1975 г. Л.В.Канторович и Т.Купманс получили Нобелевскую премию по экономике. В конце сороковых годов ХХ века Дж. Данциг - американский математик, автор основного метода решения задач ЛП – симплекс-метода. ЛП изучает задачи на экстремум линейной функции при линейных ограничениях.

Линейное программирование. Постановка задач ЛП. 6 Постановка задач ЛП Пусть имеются элементы некоторого множества, идентификацию которых можно провести с помощью n координат (численных значений показателей, факторов и др.), тогда здесь можно говорить о некотором векторном пространстве, где элементы есть n-мерные вектора.

Линейное программирование. Постановка задачи ЛП. 7 Пусть задана некоторая линейная функция многих переменных F(x) или и требуется найти вектор x, который будет максимизировать (минимизировать) эту функцию при линейных ограничениях:

Линейное программирование. Постановка задач ЛП. 8 Введем матрицу коэффициентов А, вектор правых частей b и вектор c: Будем дополнительно считать, что все компоненты вектора x не отрицательны, тогда задачу (1) будем считать стандартной задачей ЛП на максимум целевой функции F(x). (1)

Линейное программирование. Примеры задачи ЛП. 9 Пример задачи ЛП (Оптимальная стратегия банка) Пусть собственные средства банка в сумме с депозитами составляют 100 млн.$. Правление банка, учитывая ситуацию на рынке и рекомендации финансовых аналитиков считает, что часть этих средств, не менее 35 млн.$, должна быть размещена в кредитах (основной способ заработка для банков) и средний процент годовой прибыли от кредитов пусть составляет 10%. Кредиты являются неликвидными активами банка, т.к. в случае непредвиденных обстоятельств обратить кредиты в деньги без существенных потерь невозможно.

Линейное программирование. Пример задачи ЛП. 10 Другое дело ценные бумаги, особенно государственные. Эти ценные бумаги всегда можно продать с небольшой прибылью, поэтому существует правило – коммерческие банки должны покупать в определенной пропорции ликвидные активы (ценные бумаги, облигации и т.д.), чтобы компенсировать неликвидные активы. Считается, что в данной экономической ситуации, ценные бумаги должны составлять не менее 30% средств, размещенных в кредитах и ценных бумагах. Ставку прибыли от ликвидных активов примем 2% годовых. Цель банка состоит в том, чтобы получить максимальную прибыль за год от размещения средств в кредитах и ценных бумагах.

Пример задач ЛП. Мат.модель задачи. 11 Математическая модель задачи Построим Математическую модель задачи 1. Введем переменные: Пусть – это сумма средств банка, направляемых в кредиты, а – сумма средств банка, размещенных в ценных бумагах. Тогда имеем:

Пример задач ЛП. Мат.модель задач ЛП. 12 2. Введем ограничения на значения плана или на параметры стратегии банка х: – ограничение по ресурсам, – ограничение по кредитам (первое правило банка), – ликвидные активы должны быть в объеме не менее 30 % от всех ресурсов банка (второе правило банка).

Пример задач ЛП. Мат.модель задач ЛП. 13 3. Введем целевую функцию (критерий) – прибыль банка: Решение задачи заключается в нахождении неотрицательных значений переменных и , удовлетворяющих линейным неравенствам в пункте 2 и максимизирующих линейную формулу в пункте 3.

Графический метод решения задач ЛП. 14 Графический метод решения задачи ЛП Если задача ЛП содержит только две переменные, то такую задачу ЛП можно исследовать и решить графически. Рассмотрим задачу (2) (3) (4)

Графический метод решения задач ЛП. 15 На плоскости любое из неравенств (3) определяет полуплоскость, лежащую по одну из сторон от прямой . Для того чтобы определить расположение этой полуплоскости относительно граничной прямой, можно подставить координаты какой-либо точки (при проще всего взять начало координат) в соответствующее неравенство (3) и проверить его выполнение.

Графический метод решения задач ЛП. 16 Таким образом, допустимое множество М задачи (2)-(4) является пересечением первого квадранта и полуплоскостей, соответствующих неравенствам (4). Поэтому множество М представляет собой либо: а) пустое множество, тогда задача (2)-(4) не имеет решений из-за несовместности ограничений (3), (4); б) многоугольник (рис. 1); в) неограниченное многоугольное множество (рис. 2).

Графический метод решения задач ЛП. 17

Графический метод решения задач ЛП. 18 Для решения задачи (2)-(4) в случае (допустимое множество - непустое множество) рассмотрим семейство линий уровня функции L(x) из (2) (5) которые являются параллельными прямыми для различных значений C. Вектор антиградиента (здесь символ «T» означает транспонирование вектора-строки в вектор-столбец перпендикулярен к прямым (5) и этот вектор указывает направление убывания L(x) (вектор градиент показывает направление возрастания функции).

Графический метод задач ЛП. 19 Если перемещать параллельно самой себе произвольную прямую (5), проходящую через допустимое множество M, в направлении убывания L(x) до тех пор, пока эта прямая будет иметь хотя бы одну общую точку с множеством M, то в своем крайнем положении указанная прямая пройдет через точку множества M, в которой целевая функция L(x) принимает минимальное на M значение.

Графический метод решения задачи о банке 20 Графический метод решения задачи о банке Теперь вернемся к нашей задаче о банке и построим допустимое множество планов (стратегий) банка. Каждое ограничение порождает допустимое множество точек на плоскости, и их пересечение дает нам допустимое множество стратегий банка – треугольник АВС. Координаты точек указаны на рисунке 3.

Графический метод решения задачи о банке. 21

Графический метод решения задачи о банке. 22 Затем проведем прямую через начало координат (линия нулевой доходности) и будем передвигать ее по направлению градиента или нормали, т.е. по направлению возрастания функции доходности. Первой точкой встречи прямой с допустимым множеством есть точка С(35;15). Имеем млн. долл.

Графический метод решения задачи о банке. 23 Это есть минимальное значение прибыли банка при такой допустимой стратегии банка. Перемещая Линию доходности вдоль допустимого множества в том же направлении нормали к линии уровня критерия оптимальности получаем увеличение прибыли и максимальное значение прибыли достигается на границе допустимого многогранника планов в точке В(70;30), где млн. долл.

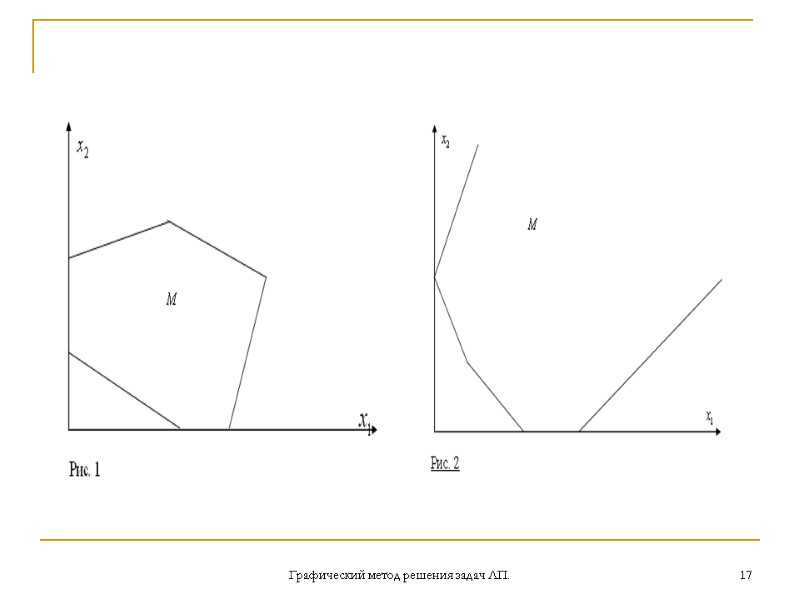
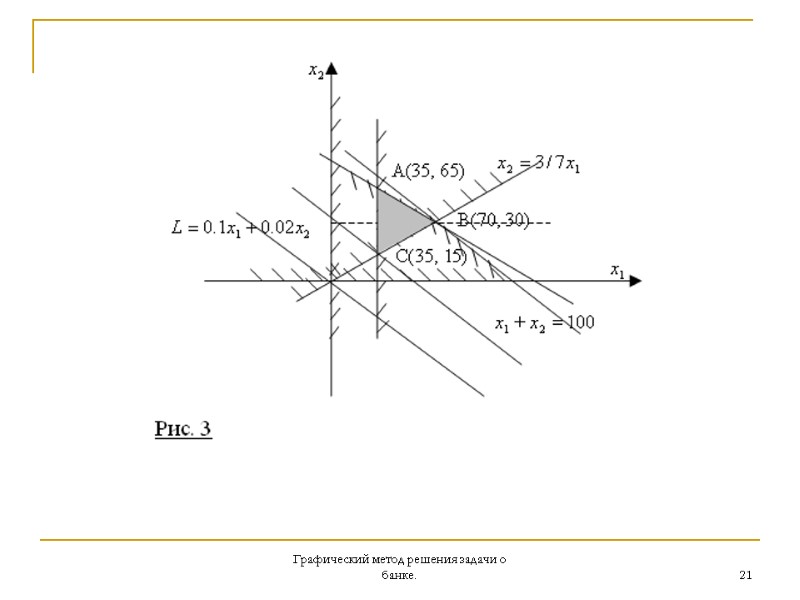
Графический метод решения задачи о банке. 24 Замечание 1: допустимое множество есть выпуклое множество (Множество М называется выпуклым, если вместе с любыми допустимыми точками множества ему принадлежат и все точки отрезка, соединяющего эти точки). Замечание 2: допустимое множество на плоскости – многоугольник, а в пространстве – многогранник. Замечание 3: оптимальное решение в задаче ЛП находится в вершине или стороне многоугольника (в вершине или на ребре или на грани многогранника).

Линейное программирование. Стандартная задача на максимум. 25 Стандартная задача на максимум. Это задача линейного программирования на максимум прибыли в условиях n технологий или задача об оптимальном «ассортименте». Пусть требуется найти план производства в условиях существования n технологий производства (например, выпуска n видов продукции).

Линейное программирование. Стандартная задача на максимум. 26 Имеется m видов ресурсов, необходимых для производства. Известны данные {aij} об удельных затратах i ресурса при единичной интенсивности j технологии (затраты i ресурса на изготовление одной единицы продукции j вида), а также критерий интенсивности плана производства, например, показатели прибыли для каждой технологии (при единичной интенсивности j технологии) и пусть cj- прибыль (эффект) единичной интенсивности j технологии.

Линейное программирование. Стандартная задача на максимум. 27 Итак требуется найти план производства, максимизирующий прибыль при имеющихся запасах ресурсов b1,...bm. и заданной «технологической» матрицей.

Линейное программирование. Стандартная задача на максимум. 28 Опишем этапы построения Математической модели. 1. Введем переменные: количество единиц продукции j вида или интенсивность j «технологии». Итак под x будем понимать план производства – вектор-строка выпуск, производство которого стеснено ресурсами.

Линейное программирование. Стандартная задача на максимум. 29 2. Введем ограничения: На примере первого ресурса покажем как его удельные затраты и запас формируют первое ограничение. Т.к. a11x1- затраты первого ресурса(например сырья) на выпуск всех изделий первого вида, a12x2 – затраты сырья на выпуск всех изделий второго вида, a12xn – затраты сырья на выпуск всех изделий вида n, а их сумма есть общие затраты первого ресурса на выпуск плана х, то общие затраты первого ресурса не могут превысить его запас и поэтому

Линейное программирование. Стандартная задача на максимум. 30 Аналогично получаются и другие ресурсные ограничения. Итак, имеем

Линейное программирование. Стандартная задача на максимум. 31 3. Введем целевую функцию (критерий) - критерий эффективности для плана x: т.к. – прибыль от реализации всех единиц продукции первого вида, – прибыль от реализации всех единиц продукции второго вида и т.д. 4. Решение и анализ задачи ЛП. Задача определения оптимального производственного плана есть задача на максимум ЛП. Даная задача может быть решена графическим методом (с которым познакомились ранее) и симплекс-методом.

Линейное программирование. Симплекс-метод задач ЛП. 32 Симплекс-метод решения задач ЛП Рассмотрим здесь реализацию симплекс-метода для задачи об оптимальном ассортименте на конкретном примере. Пусть заданы три технологии (три вида продукции), «технологическая» матрица удельных затрат двух видов ресурсов, т.е. затрат ресурсов при единичной интенсивности каждой технологии производства и показатели удельной прибыли.

Линейное программирование. Симплекс-метод задач ЛП. 33 Требуется найти максимум линейной функции прибыли при условиях, что переменные удовлетворяют ограничениям на ресурсы и неотрицательны.

Линейное программирование. Симплекс-метод задач ЛП. 34 Сначала опишем построение так называемых первоначальных опорных планов задачи. Введем дополнительные неотрицательные переменные по числу ограничений-неравенств, сводящих эти неравенства к равенствам. Их экономический смысл – неиспользуемая часть соответствующего ресурса. Имеем

Линейное программирование. Симплекс-метод задач ЛП. 35 Полученная система двух линейных уравнений с пятью неизвестными имеет бесчисленное множество решений. Но нам нужны только неотрицательные решения, которые представляют собой вектора в 5-мерном пространстве. Каждое из этих решений является претендентом на план. Но как упорядочить множество таких планов задачи. Здесь вводится понятие базисного решения. Если в последней системе за базисные переменные принять и , а в качестве свободных переменных принять основные переменные, то из этой системы можно однозначно выразить дополнительные переменные через свободные.

Линейное программирование. Симплекс-метод задач ЛП. 36 Однозначность есть следствие невырожденности определителя максимального ранга, т.е. минора второго порядка, порождаемого переменными и Полагая теперь свободные переменные равными нулю, мы получаем стартовое базисное неотрицательное решение (0,0,0,100,150) для множества планов задачи. В качестве базисных переменных можно сразу взять и любые другие две, если они образуют невырожденный минор максимального ранга (здесь минор максимального ранга имеет размерность два) и при нулевых значениях свободных переменных эти новые базисные переменные будут неотрицательными.

Линейное программирование. Симплекс-метод задач ЛП. 37 Первая симплекс-таблица состоит из 8 столбцов. Две строки таблицы соответствуют линейным ограничениям, а последняя – критерию. В первом столбце размещаются названия базисных переменных и обозначение целевой функции. Второй столбец содержит соответствующие их значения вдоль выбранного базиса. Следующие столбцы отвечают переменным задачи и содержат коэффициенты матрицы ограничений, а в последней (оценочной) строке – коэффициенты целевой функции с противоположным знаком. Итак, начальная таблица построена.

Линейное программирование. Симплекс-метод задач ЛП. 38 Начинаем итерации симплекс-преобразований. Просматриваем оценочную строку. Если в ней нет отрицательных коэффициентов, то план из текущих базисных переменных - оптимальный.

Линейное программирование. Симплекс-метод задач ЛП. 39 Если – есть, то продолжаем итерации, выбирая для этого максимальный по модулю отрицательный коэффициент(наименьшую отрицательную оценку). Этот столбец (здесь столбец при х2 ) называется ведущим(разрешающим) и переменную х2 будем вводить в базис. Но вместо какой переменной? Для этого просматриваем положительные коэффициенты ограничений разрешающего столбца (здесь они у нас все положительны), а если их нет, то задача неразрешима. С положительными коэффициентами aij образуем отношения bi/aij , заносим их в последний столбец таблицы и выбираем из этих отношений минимальное.

Линейное программирование. Симплекс-метод задач ЛП. 40 Строка с указанным минимальным отношением называется разрешающей(ведущей), а ее элемент, стоящий на пересечении с разрешающим столбцом называется разрешающим(ведущим, ключевым) на данной итерации. В нашем примере, отвечающая этой второй строке, базисная переменная х5 выводится из плана и вместо нее вводится х2 (разрешающим элементом у нас является а22 =4). Теперь производятся преобразования всех коэффициентов симплекс таблицы по так называемому алгоритму Жордана - Гаусса (алгоритм последовательного исключения неизвестных при решении систем линейных уравнений). Ему соответствует такое правило изменения коэффициентов.

Линейное программирование. Симплекс-метод задач ЛП. 41 «В разрешающей строке все числа делятся на разрешающий элемент, в разрешающем столбце – все элементы, кроме разрешающего, становятся нулями, а вместо разрешающего элемента появляется единица. Остальные коэффициенты предыдущей таблицы изменяются по так зазываемому правилу «прямоугольника». Для каждого элемента вводится прямоугольник, в котором главная диагональ соединяет клетку с выбранным элементом и разрешающим. Правило «прямоугольника» - новое значение коэффициента равняется старому минус произведение элементов на неглавной диагонали прямоугольника, деленное на разрешающий элемент.

Линейное программирование. Симплекс-метод задач ЛП. 42 Первая итерация

Линейное программирование. Симплекс-метод задач ЛП. 43 Вторая итерация

Линейное программирование. Симплекс-метод задач ЛП. 44 Как видим в оценочной строке нет отрицательных оценок, следовательно после двух итераций мы нашли оптимальное решение х=(10;35;0;0;0)Т, т.е. для максимума прибыли план выпуска должен быть следующим – продукция первого вида – в количестве 10 единиц, 2 вида – 35 единиц, третий вид продукции не выпускается, оба ресурса при таком плане расходуются полностью и при этом максимальное значение прибыли равно 125.

Линейное программирование.Теория двойственности. 45 Теория двойственности Рассмотрим две задачи Оказывается, что задачи (6) и (7), по смыслу совершенно различные, могут быть формально связанными отношением так называемой двойственности. (6) (7)

Линейное программирование.Теория двойственности. 46 Введем двойственные переменные для задачи (6) – неотрицательный вектор y, вектор двойственных переменных Здесь yi – условная оценка (условная, «теневая» цена) i-го ресурса. Тогда двойственной задачей к (6) будет задача (7)

Линейное программирование.Теория двойственности. 47 Т.е. прямую и двойственную к ней задачи можно записать так

Линейное программирование.Первая теорема двойственности. 48 Первая теорема двойственности Задачи (6) и (7) одновременно разрешимы. Если x*, y* – оптимальные решения пары задач, то Экономический смысл первой теоремы двойственности: Согласно первой теореме двойственности имеем . Величина имеет

Линейное программирование.Первая теорема двойственности. 49 размерность стоимости (цена, умноженная на объем продукции). Следовательно, имеет ту же размерность. Поскольку - вектор объемов ресурсов, то - в некотором роде вектор цен на ресурсы. Максимальная прибыль задачи сопровождается наилучшей оценкой использования ресурсов или максимальной эффективности использования технологий отвечает наилучшая оценка используемых ресурсов. Двойственные оценки помогают ответить на вопрос, какова наименьшая

Линейное программирование.Первая теорема двойственности. 50 стоимость набора ресурсов, дающая возможность обращения ресурсов в продукты и продажи этих продуктов с целью максимизации прибыли. При оптимальных значениях и и экономической системе или фирме безразлично, использовать ли ресурсы для производства и продать продукты, чтобы получить , или продать ресурсы по ценам , так как для них

Линейное программирование.Вторая теорема двойственности. 51 Вторая теорема двойственности Для того чтобы пара планов x*, y* была оптимальной в прямой и двойственной задачах соответственно, необходимо и достаточно, чтобы выполнялись следующие условия:

Линейное программирование.Вторая теорема двойственности. 52 Экономический смысл второй теоремы двойственности: 1. Если xj>0, j-ая технология рентабельна (соответственно, j-ое ограничение двойственной задачи, которое характеризует условные удельные

Линейное программирование.Вторая теорема двойственности. 53 оценки затрат ресурсов при выпуске одной единицы продукции j-го вида, выполняется как строгое равенство), то условная удельная оценка всех используемых ресурсов при производстве одной единицы продукции j вида равна прибыли cj. И наоборот, если условная оценка удельных затрат используемых ресурсов равна прибыли cj, то данная технология рентабельна. 2. Если xj=0, т.е. j-ая технология нерентабельна, то условная удельная оценка затрат больше удельной прибыли. И наоборот, если условная удельная оценка затрат ресурсов больше удельной прибыли,

Линейное программирование.Вторая теорема двойственности. 54 технология нерентабельна. 3. Если yi>0 (условная цена i-го ресурса отлична от 0), то весь i-ый ресурс расходуется полностью. Наоборот, если (i-ый ресурс используется полностью), то у него есть ненулевая «цена», как мера его дефицитности. Эти «цены» в сравнении с собой устанавливают некоторую упорядоченность среди дефицитных ресурсов (чем больше «цена», тем более дефицитен ресурс). 4. Если цена равна 0, т.е. i-ый ресурс недефицитен, тогда соответствующее ограничение по расходу i-го ресурса выполняется как строгое неравенство.

Линейное программирование.Третья теорема двойственности. 55 Третья теорема двойственности Если двойственная оценка yi*>0, то вдоль оптимального плана x* эта оценка yi* есть частная производная функции L по i-му аргументу, т.е. Третью теорему двойственности можно использовать для приближенного определения

Линейное программирование.Третья теорема двойственности. 56 изменения прибыли в исходной задаче при изменении дефицитных ресурсов без решения новой задачи с измененными ресурсами. Пусть в некоторой задаче имеем

Линейное программирование.Третья теорема двойственности. 57 Определим новое приближенное значение прибыли, не решая заново задачу симплекс-методом, при условии изменения первого ресурса на 10% - а второго – на 20% - . Тогда прибыль с изменением объема ресурсов будет рассчитываться по формуле Где изменение прибыли :

Линейное программирование.Третья теорема двойственности. 58 Имеем Итак приближенное значение максимальной прибыли: L = 1000 +283=1283.

Линейное программирование.Транспортная задача. 59 Транспортная задача Транспортная задача (ТЗ) является одной из задач ЛП. С помощью алгоритма и модели ТЗ решаются не только транспортные задачи, но и многие другие проблемы, например задачи распределительные. Модель транспортной задачи характеризуется многоиндексными неизвестными. Эти задачи можно свести к предыдущим задачам, но при этом полученные задачи ЛП будут высокой размерности и матрицы ограничений будут содержать много нулей. Решение таких задач возможно также симплекс-методом, но это решение не будет эффективно,

Линейное программирование.Транспортная задача. 60 т.к. не учитывает специфики постановки задачи, и поэтому желателен метод решения задачи, учитывающий её особенности. Одним из таких методов и является метод потенциалов, который рассмотрим ниже.

Линейное программирование.Пример постановки ТЗ. 61 Пример постановки ТЗ Пусть имеется m предприятий, которые производят (накапливают) некий однородный продукт в количествах а1, а2,..., аm единиц, и n потребителей этого продукта, которым необходимо соответственно не менее b1, b2,..., bn единиц. Также известна стоимость перевозки единицы продукта из i пункта отправления в j пункт назначения (для всех маршрутов), она равна сij . Необходимо найти план перевозок, при котором общие затраты на перевозку продукции были бы минимальными.

Линейное программирование.Пример постановки ТЗ. 62 Модель ТЗ играет важную роль для фирм с большим количеством филиалов и партнеров и лежит в основе их поведения. Транспортная логистика – это область принятия решений, базирующаяся на алгоритмах решения транспортных задач.

Линейное программирование.Математическая модель ТЗ. 63 Математическая модель ТЗ 1. Введем переменные xij - объем продукции, который отправляет i поставщик j потребителю. 2. Построим ограничения по поставщикам и потребителям

Линейное программирование.Математическая модель ТЗ. 64 В практике планирования используются также дополнительные условия: каждый поставщик должен вывезти всё, что у него есть, а каждый потребитель должен получить столько, сколько ему надо. В этой ситуации ограничения по потребителям и поставщиками выглядят как строгие равенства. Ограничения в этом случае принимают вид - балансовые ограничения по поставщикам - балансовые ограничения по потребителям

Линейное программирование.Математическая модель ТЗ. 65 3. Построим критерий оптимальности – суммарные затраты на поставки Итак, требуется найти оптимальный план X=(xij) , при котором целевая функция L(x) достигает своего минимального значения, т.е. требуется решить следующую задачу оптимизации

Линейное программирование.Математическая модель ТЗ. 66 Такие задачи целесообразно решать при помощи особого варианта симплекс-метода — так называемого метода потенциалов. Далее везде предполагаем, что ТЗ “закрытая”. где есть количество продукции, находящееся на складе i, и — потребность потребителя j или суммарный “спрос” равен суммарному (8) , (9)

Линейное программирование.Математическая модель ТЗ. 67 Замечание. Если “спрос” больше “предложения”, т.е. , то количество продукции, равное , недостает и его надо дополнительно произвести. В этом случае мы вводим фиктивного» производителя (склад) или поставщика m+1 с мощностью и полагаем транспортные расходы равными 0 для всех j. Если “предложение” больше “спроса” , то необходимо ввести дополнительного (n+1)-го потребителя с

Линейное программирование.Математическая модель ТЗ. 68 потребностью или “емкостью” и при этом транспортные затраты полагаем равными 0 для всех i и тогда задача опять становится закрытой. Ситуация с открытой ТЗ равносильна наличию в исходной постановке в ограничениях, вместо равенств, неравенств, например ,что соответствует возможности неполного вывоза груза из пунктов отправления. Нетрудно видеть, что такая постановка задачи может быть сведена к рассмотренной выше постановке путем введения дополнительного

Линейное программирование.Математическая модель ТЗ. 69 фиктивного потребителя Bn+1, который характеризуется потребностью в грузе и тарифами перевозок Обычно данные ТЗ записываются в виде следующей таблицы (транспортной таблицы) (смотри следующий слайд.)

Линейное программирование.Математическая модель ТЗ. 70

Линейное программирование.Некоторые теоретические сведения. 71 Некоторые теоретические сведения ТЗ является частным случаем основной задачи ЛП, следовательно, минимальное значение целевой функции достигается в вершине многогранника решений (опорном плане). Число компонент xij в плане ТЗ с m поставщиками и n потребителями равно mхn, а число уравнений в (8) равно m+n. Ограничившись рассмотрением только закрытых моделей, мы предполагаем выполнение условия (9), что уменьшает ранг системы в (8) на единицу. Таким образом, опорный план ТЗ может иметь не более n+m-1 отличных от нуля переменных.

Линейное программирование.Некоторые теоретические сведения. 72 Определение 1. Если опорный план имеет n+m-1 отличных от нуля переменных, то он называется невырожденным, а если меньше – то вырожденным. Лемма 1. Допустимый план ТЗ является опорным, если из ненулевых перевозок этого плана нельзя составить замкнутый цикл. Теорема 1 (О существовании решения ТЗ). Для разрешимости транспортной задачи ЛП необходимо и достаточно выполнение условия (9), т.е. чтобы модель ТЗ была закрытой. Эта теорема дает критерий существования решения ТЗ, ограничивая класс задач, подлежащих дальнейшему рассмотрению, закрытыми моделями.

Линейное программирование.Некоторве теоретические сведения. 73 Если же постановка задачи приводит к построению открытой модели, то, как показано выше, она может быть сведена к закрытой модели.

Линейное программирование.Методы определения опорных планов ТЗ. 74 Методы определения опорных планов ТЗ Для нахождения первоначального опорного плана имеется несколько методов. Наиболее популярными из них являются метод северо-западного (С-З) угла и метод минимального элемента. В методе северо-западного угла первой заполняется С-З клетка. Эта поставка либо полностью удовлетворяет спрос первого потребителя, если предложение первого поставщика достаточное для этого, либо, в противном случае, полностью используется предложение первого поставщика. После этого вычеркивается либо первый столбец, либо, во

Линейное программирование.Методы определения опорых планов ТЗ. 75 втором случае, первая строка. Затем в оставшейся части таблицы находится опять крайняя С-З клетка и все повторяется сначала. В методе минимального элемента, который часто оказывается более эффективным, по сравнению с методом С-З угла, последовательно, с сохранением баланса по спросу и предложению, заполняются поставками клетки транспортной таблицы с минимальной стоимостью.

Линейное программирование.Метод определения оптимальных планов ТЗ. 76 Метод определения оптимальных планов ТЗ При определении оптимального плана ТЗ (как и в более общем случае основной задачи ЛП) встает вопрос о возможности формулирования необходимого и достаточного условия оптимальности. Ответ на этот вопрос дает следующая теорема. Теорема 2 (О потенциалах): Если для некоторого опорного плана X=(xij) транспортной задачи (34) существуют такие числа u1, u2, …, um, и v1, v2, …,vn, называемые потенциалами, такие что

Линейное программирование.Метод определения оптимальных планов ТЗ. 77 при (10) при (11) для всех то X=(xij) – оптимальный план транспортной задачи. Метод потенциалов является частным случаем симплекс-метода, который учитывает специфику ограничений ТЗ. Доказательство теоремы 2 о потенциалах проводится прямым применением второй теоремы двойственности. При этом потенциалы рассматриваются как переменные задачи, двойственной к транспортной задаче.

Линейное программирование.Метод определения оптимальных планов ТЗ. 78 Определение 2:Циклом (циклом пересчета) в таблице ТЗ называется ломаная линия, вершины которой (точки, в которых ломаная меняет направление) расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем одно звено каждой вершины находится в строке, а другое в столбце. Точки пересечения звеньев цикла не являются вершинами. Лемма 2 (О возможности построения цикла): Добавляя любую свободную (незанятую) клетку к занятым клеткам транспортной таблицы, соответствующим невырожденному опорному

Линейное программирование.Метод определения оптимальных планов ТЗ. 79 плану ТЗ, всегда можно построить цикл пересчета, в который в качестве вершин будут входить некоторые из этих клеток (но свободная клетка обязательно). Лемма 3 (О единственности цикла пересчета): Множество клеток таблицы ТЗ, состоящее из произвольно выбранной свободной клетки и занятых клеток, соответствующих базисным компонентам опорного плана может содержать лишь один цикл пересчета. Доказательство этих утверждений основывается на аналогичных утверждениях из общей теории ЛП о

Линейное программирование.Метод определения оптимальных планов ТЗ. 80 о свойствах опорных планов (вершин многогранника решений) основной задачи ЛП. Рассмотрим процедуру, называемую сдвигом по циклу пересчета. Эта процедура состоит в переходе от ранее полученного плана к новому опорному плану, содержащему, в качестве базисной, ранее свободную переменную. Соответствующая этой переменной свободная клетка вместе с некоторыми из занятых клеток ранее полученного опорного плана составляют цикл. Далее необходимо «переместить грузы» в пределах цикла. Это перемещение производится по следующим правилам:

Линейное программирование.Метод определения оптимальных планов ТЗ. 81 1) каждой из клеток, связанных циклом с данной свободной клеткой, приписывают определенный знак, причем свободной клетке – знак плюс, а всем остальным клеткам при движении вдоль цикла – поочередно знаки минус и плюс (эти клетки называют минусовыми и плюсовыми); 2) в свободную клетку переносят минимальное из значений перевозок хij, стоящих в минусовых клетках. Одновременно это число прибавляют к значениям перевозок, стоящим в плюсовых клетках, и вычитают из значений перевозок, стоящих в минусовых клетках.

Линейное программирование.Метод определения оптимальных планов ТЗ. 82 Клетка, которая ранее была свободной, становится занятой, а клетка, в которой стояло минимальное среди минусовых клеток значение перевозок, считается свободной. В результате указанных «перемещений груза» в пределах клеток, связанных циклом с данной свободной клеткой, определяют новый опорный план ТЗ. Данная процедура по своему смыслу полностью аналогична процедуре перехода в рамках симплексного метода от одного опорного плана основной задачи ЛП к другому с помощью жордановского исключения. Процедура сдвига по циклу пересчета играет ту же роль в методе потенциалов.

Линейное рограммирование.Метод потенциалов. 83 Метод потенциалов Процесс нахождения решения ТЗ методом потенциалов включает следующие этапы: 1. Нахождение первого опорного плана (например, одним из приведенных выше методов). При этом число заполненных клеток должно быть равным m+n-1. 2. Нахождение потенциалов, соответствующих этому опорному плану из уравнений (10) с учетом дополнительного соотношения u1=0.

Линейное программирование.Метод потенциалов. 84 3. Определение оценок u1+vj-cij для всех свободных клеток таблицы планирования. Если среди них нет положительных, то получен оптимальный план ТЗ; если же они имеются, то необходимо переходить к новому опорному плану. 4. Среди положительных оценок свободных клеток выбирается максимальная, и для данной свободной клетки строится цикл и производится сдвиг по циклу пересчета. Построив новый опорный план, необходимо перейти к этапу 2 и продолжить последовательное выполнение

Линейное программирование.Метод потенциалов. 85 этапов до тех пор, пока проверка знаков оценок на этапе 3 не позволит сделать вывод о нахождении оптимального плана ТЗ. Необходимость дополнения уравнений (10) дополнительным соотношением u1 = 0, вызвана тем, что система (10) состоит из m+n-1 линейно независимых уравнений, но содержит m+n неизвестных Тем самым, для однозначного решения системы (10) недостает одного уравнения. Неоднозначность определения потенциалов не сказывается на алгоритме. ).

Линейное программирование.Метод потенциалов. 86 Очевидно, что количество итераций, необходимых для получения решения ТЗ методом потенциалов, существенно будет зависеть от выбора первого опорного плана.

Линейное программирование.Пример решения ТЗ методом потенциалов. 87 Пример решения ТЗ методом потенциалов Пример. Пусть имеется 3 склада, число единиц продукции на которых, соответственно, равно 20, 50, 30, и четыре потребителя, которым необходимо доставить 10, 45, 10, 35 единиц продукции, соответственно, а таблица затрат имеет вид, как показано на таблице 19. Найти план перевозок с минимальными затратами.

Линейное программирование.Пример решения ТЗ методом потенциалов. 88 Таблица.

Линейное программирование.Пример решения ТЗ методом потенциалов. 89 Решение. Сначала в три этапа построим математическую модель: 1. Введем неизвестные: В качестве переменных модели введем - количество груза, перевозимого из пункта отправления Ai в пункт потребления Bj , естественном условии неотрицательности перевозок. 2. Построим ограничения - а) по поставщикам

Линейное программирование.Пример решения ТЗ методом потенциалов. 90 (количество груза, вывезенного из пункта отправления Ai, равно запасу груза в этом пункте) б) по потребителям

Линейное программирование.Пример решения ТЗ методом потенциалов. 91 (количество груза, ввезенного в пункт назначения Bj, равно потребности в грузе в этом пункте). 3. Введем критерий оптимальности: Теперь приступим к решению задачи методом потенциалов. Сначала проверяем условие (9). Конечно, здесь

Линейное программирование.Пример решения ТЗ методом потенциалов. 92 мы имеем закрытую модель ТЗ, т.к. 10+40+10+40 = 20+50+30. Приступим к решению задачи методом потенциалов. Сначала находим первоначальный опорный план. Используя метод северо-западного угла, получим:

Линейное программирование.Пример решения ТЗ методом потенциалов. 93 Убедимся, что число заполненных клеток действительно равно m+n-1=6. Опорный план невырожденный. Теперь применяем итерации метода потенциалов. Итерация 1. Находим потенциалы, соответствующие первому опорному плану, для чего построим систему уравнений: которую дополним соотношением .

Линейное программирование.Пример решения ТЗ методом потенциалов. 94 Решая эту систему, получим: После нахождения потенциалов, вычисляем потенциалы незанятых клеток по формуле Получим (значения оценок удобно записывать в левых верхних углах клеток таблицы планирования):

Линейное программирование.Пример решения ТЗ методом потенциалов. 95 Так как среди оценок имеются положительные, то найденный опорный план не является оптимальным и необходимо перейти к новому опорному плану.

Линейное программирование.Пример решения ТЗ методом потенциалов. 96 Следующий этап алгоритма – построение нового опорного плана. Наибольшей среди положительных оценок свободных клеток является 3, поэтому для данной свободной клетки строим цикл пересчета:

Линейное программирование.Пример решения ТЗ методом потенциалов. 97 Наряду с клеткой в него будут входить клетки , и Далее производим сдвиг по циклу пересчета, для чего сначала определим плюсовые (в этом примере и минусовые ( и ) клетки. Затем найдем минимальное среди значений перевозок в минусовых клетках (в нашем случае 5). Эта величина вычитается из значений перевозок в минусовых клетках и прибавляется к значениям перевозок в плюсовых клетках. и )

Линейное программирование.Пример решения ТЗ методом потенциалов. 98 При этом необходимо следить за тем, чтобы количество занятых клеток осталось равным m+n-1=6, т.е. чтобы план оставался невырожденным. Если количество занятых клеток станет меньше, то необходимо в любую свободную клетку поставить символическую поставку (например 0), так чтобы занятые клетки теперь не образовывали замкнутый контур. Итерация 2. Продолжим, начиная с п.2 выполнение алгоритма для полученного в результате первой итерации опорного плана.

Линейное программирование.Пример решения ТЗ методом потенциалов. 99 Соответствующая этому плану таблица планирования имеет вид:

Линейное программирование.Пример решения ТЗ методом потенциалов. 100 Проверим этот план на оптимальность, для чего построим систему уравнений относительно потенциалов которая вместе с дополнительным отношением дает

Линейное программирование.Пример решения ТЗ методом потенциалов. 101 Далее вычисляем оценки свободных клеток

Линейное программирование.Пример решения ТЗ методом потенциалов. 102 Среди оценок свободных клеток имеются положительные, т.е. полученный на предыдущей итерации опорный план не является оптимальным и необходимо перейти к новому опорному плану. Цикл пересчета будем строить для клетки , т.к. здесь имеется максимальная положительная оценка.

Линейное программирование.Пример решения ТЗ методом потенциалов. 103 Наряду с клеткой цикл будет включать в себя клетки , и . Минусовые клетки: , . Минимальное значение перевозок – 5. На эту величину увеличиваются значения перевозок в плюсовых клетках , и уменьшается значение перевозки в минусовой клетке . Клетка становится свободной. Итерация 3. Проверим полученный на предыдущей итерации план на оптимальность.

Линейное программирование.Пример решения ТЗ методом потенциалов. 104 Ищем потенциалы из соотношений Получим

Линейное программирование.Пример решения ТЗ методом потенциалов. 105 Далее вычисляем оценки свободных клеток

Линейное программирование.Пример решения ТЗ методом потенциалов. 106 Т. к. план не оптимален, необходимо строить цикл пересчета для клетки .

Линейное программирование.Пример решения ТЗ методом потенциалов. 107 Получаем цикл, состоящий из плюсовых клеток , , и минусовых - , , . Минимальное значение перевозки находится в клетке . Производя сдвиг по циклу пересчета получим новый опорный план, которому соответствует таблица планирования(смотри следующий слайд)

Линейное программирование.Пример решения ТЗ методом потенциалов. 108 Итерация 4. Находим потенциалы полученного на предыдущей итерации опорного плана из соотношений

Линейное программирование.Пример решения ТЗ методом потенциалов. 109 Получим

Линейное программирование.Пример решения ТЗ методом потенциалов. 110 Далее вычисляем оценки свободных клеток

Линейное программирование.Пример решения ТЗ методом потенциалов. 111 Положительных оценок нет, следовательно, найденный опорный план является оптимальным.

Линейное программирование.Пример решения ТЗ методом потенциалов. 112 При этом значение целевой функции L = 1·20+2·10+3·30+1·10+2·15+4·15 = 230. Интересно, что в данном примере оценка одной из свободных клеток в оптимальном плане равна нулю. Это означает, что задача имеет альтернативный оптимум или неединственное оптимальное решение.

Линейное программирование.Пример решения ТЗ методом потенциалов. 113 Формально продолжим процедуру метода потенциалов и построим цикл пересчета для этой клетки:

Линейное программирование.Пример решения ТЗ методом потенциалов. 114 После процедуры сдвига по циклу пересчета получим:

Линейное программирование.Пример решения ТЗ методом потенциалов. 115 Посчитав значения целевой функции на данном опорном плане, убедимся, что L=230. Таким образом, присутствие нулевой оценки одной или нескольких клеток в векторе оценок оптимального плана свидетельствует о неединственности решения задачи и, при этом, набор оптимальных решений будет описываться выпуклой линейной комбинацией полученных матричных планов (здесь двух), т.е. , где

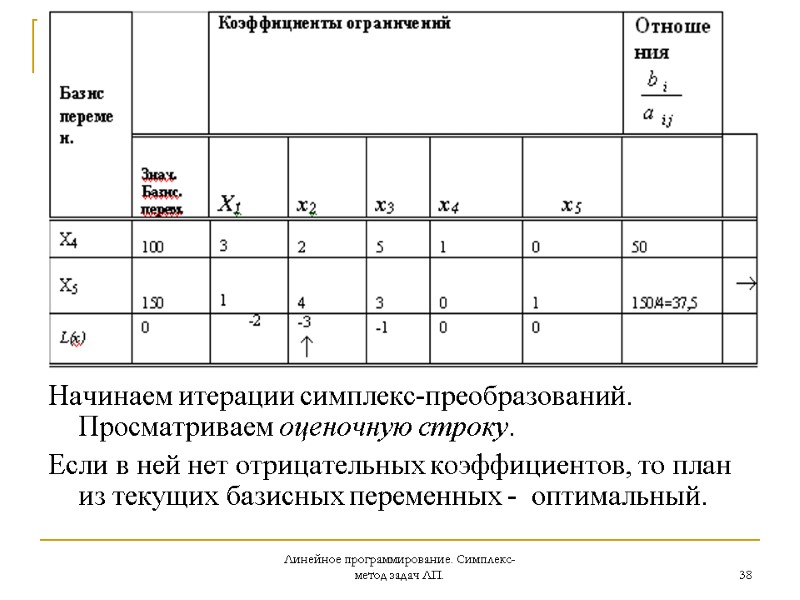
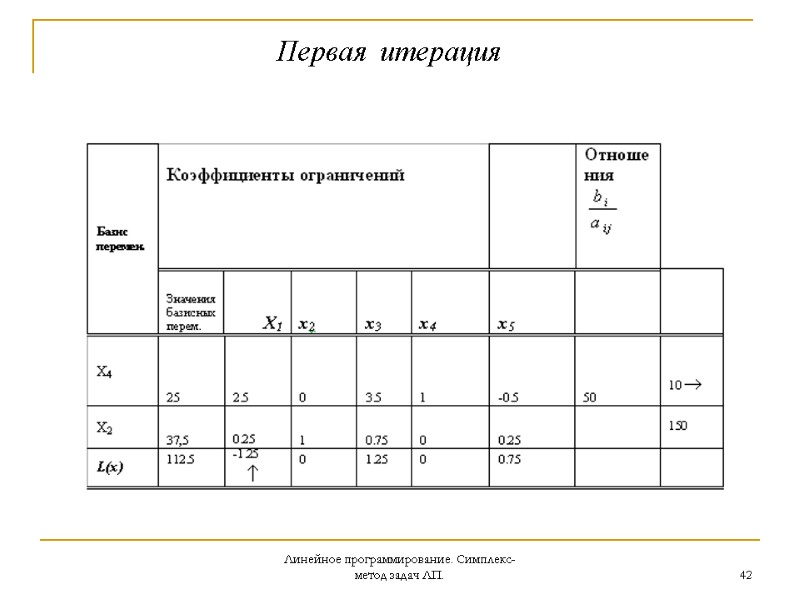
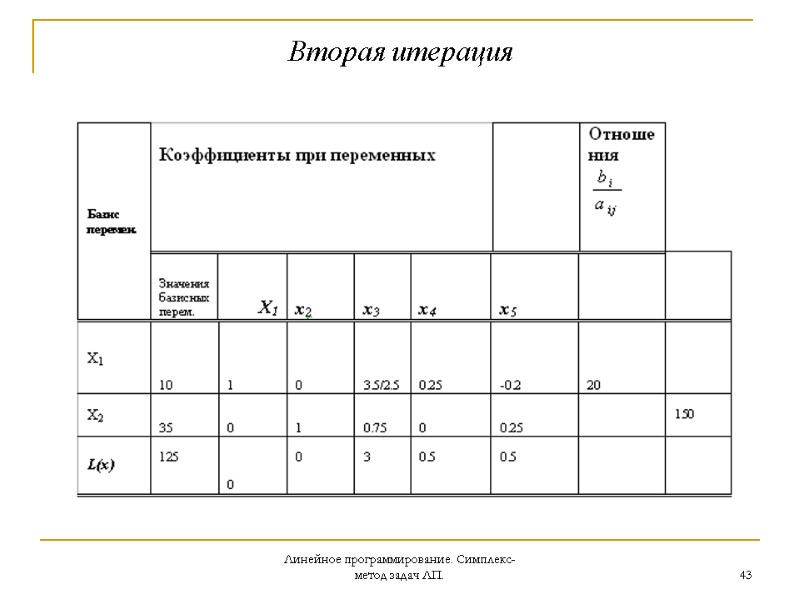
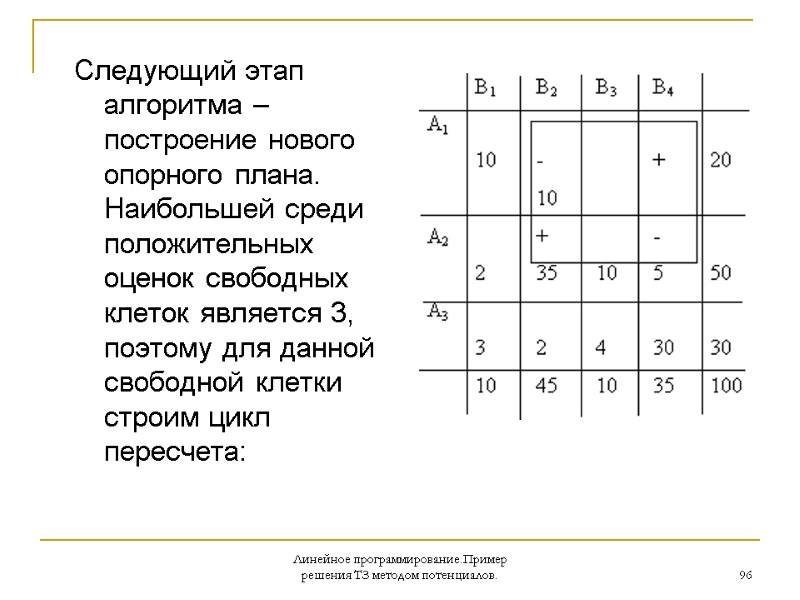
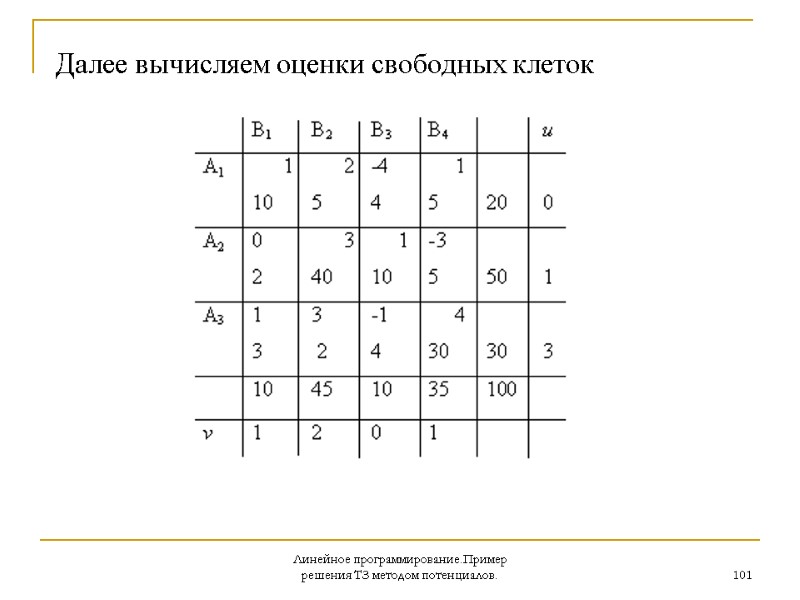
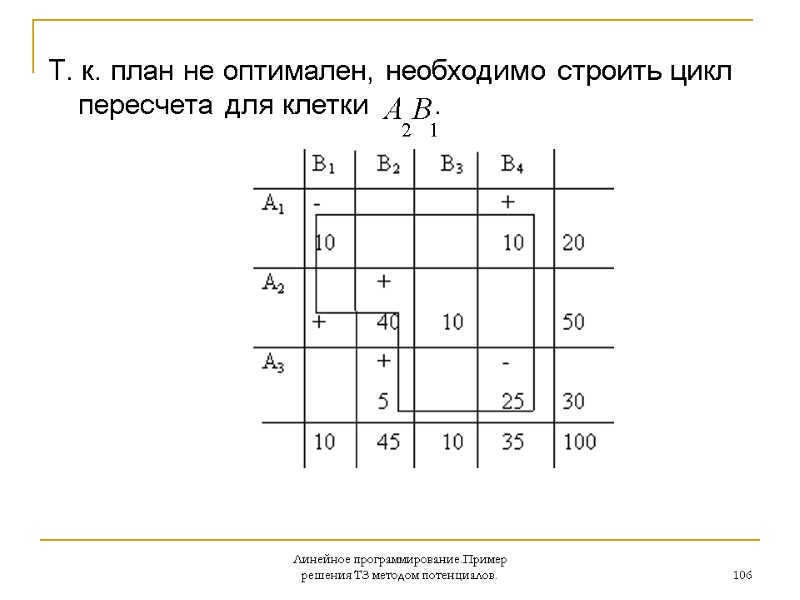
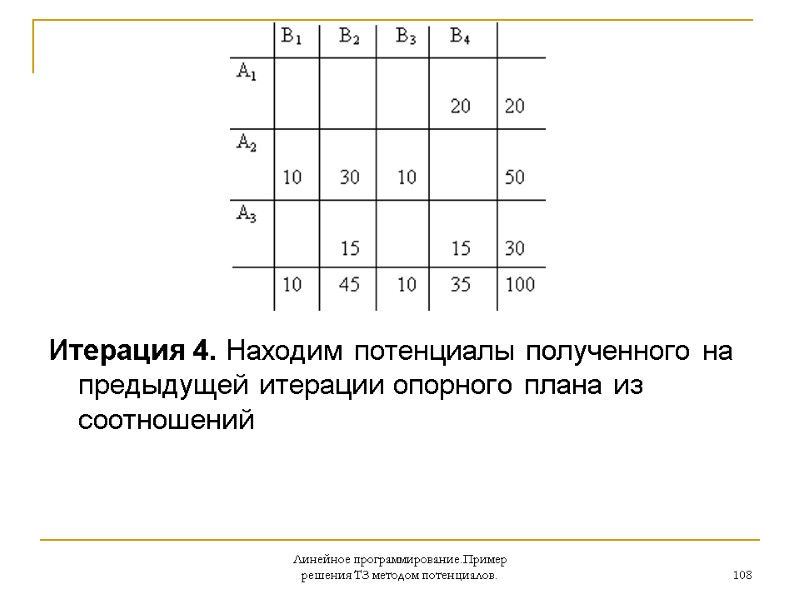
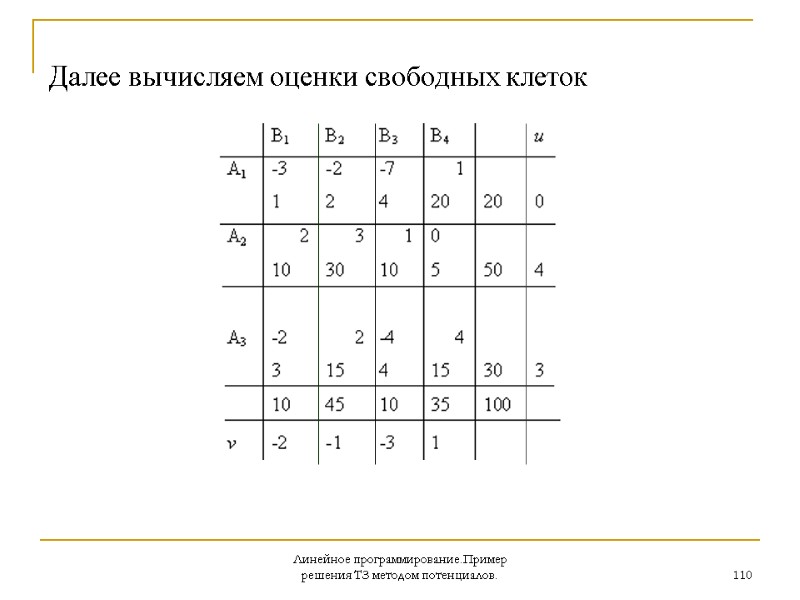
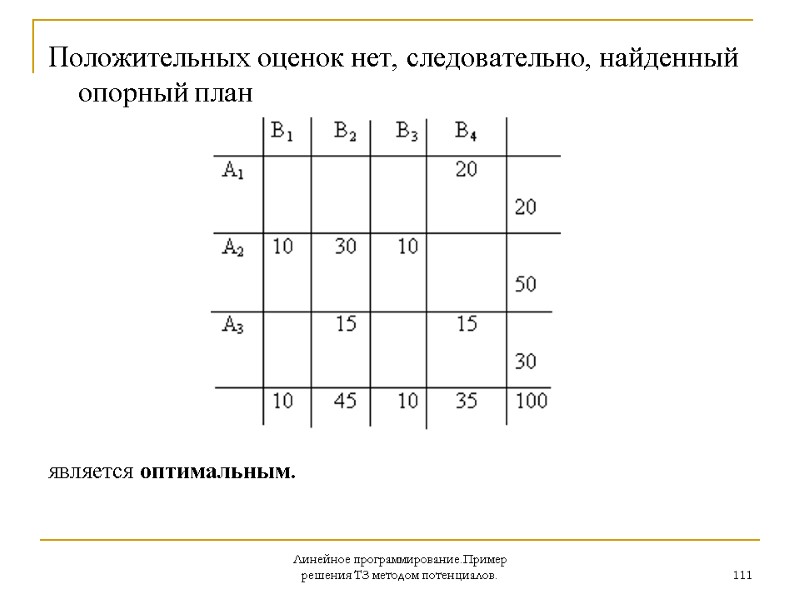
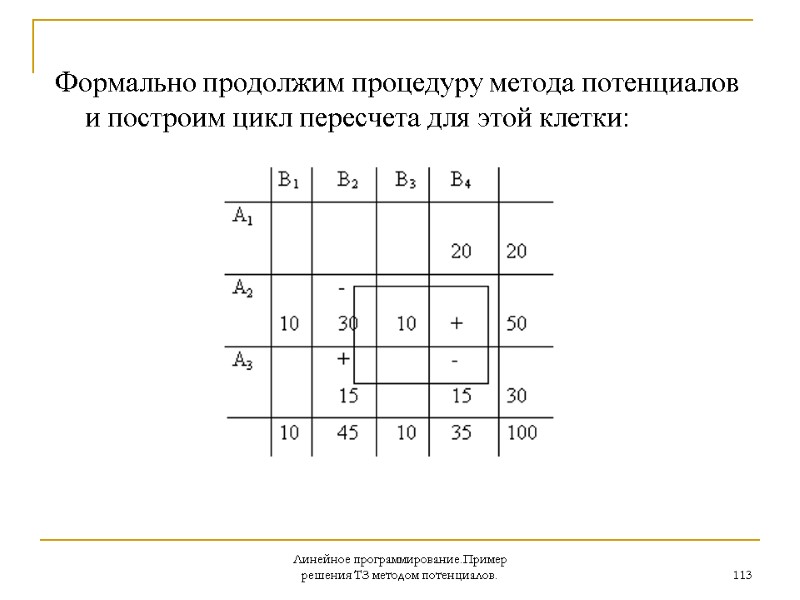
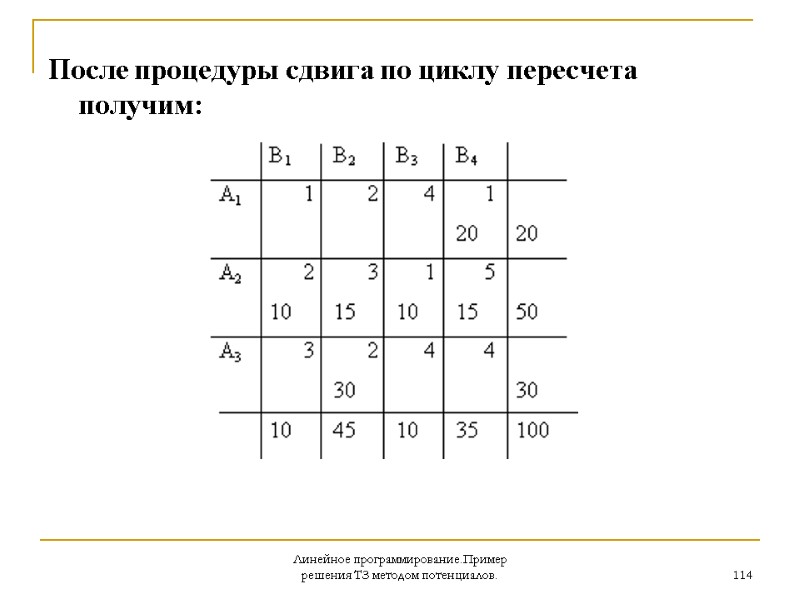
Линейное программирование.Пример решения ТЗ методом потенциалов. 116 Замечание. Выпуклой линейной комбинацией элементов Х1, Х2,…, Хn называется элемент , где коэффициенты линейной комбинации неотрицательны и в сумме равны 1, т.е. α1+α2 +…+αn =1.

Элементы теории игр 117 Элементы теории игр Принятие решений в экономике происходит в результате взаимодействия различных сторон – субъектов, предприятий, фирм и т.д. Их интересы не являются полностью совпадающими (коалиционные игры) или совпадающими (коалиционные игры); интересы могут быть противоположными (антагонистические игры); результатом действия таких партнеров является выработка компромисса в очевидных условиях конфликтности сторон. Игры также бывают неантагонистическими, кооперативными, некооперативными, парными, стратегическими и др.

Элементы теории игр 118 При описании конфликта используются следующие понятия стороны, партнеры; действия сторон – стратегии или альтернативы; интересы сторон.

Антагонистические матричные игры двух игроков 119 Антагонистические матричные игры двух игроков Рассмотрим матричные антагонистические игры или матричные игры с нулевой суммой.. Пусть имеется 2 игрока A и B. У каждого из них набор стратегий.

Антагонистические матричные игры двух игроков 120 Будем считать, что в результате выбора сторонами альтернатив или стратегий (Ai; Bk) выигрыш первого игрока равен aik. При этом проигрыш второго игрока - bik = - aik Проигрыш и выигрыш будем понимать условно, предполагая, что если у 1-го игрока aik – отрицательное количество единиц, то это значит, он проиграл соответствующую сумму денежных единиц 2-му игроку. Т.к. сумма выигрышей обоих игроков равна 0, то эти игры называются матричными играми с нулевой суммой.

Антагонистические матричные игры двух игроков. 121 А – платежная матрица игры (матрица «выигрышей»).

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 122 Гарантирующие стратегии При любых действиях первого игрока, когда он применяет чистые стратегии, он гарантирует себе минимальный выигрыш, т.е. при выборе им первой стратегии он выиграет не больше, чем При выборе остальных стратегий гарантированный результат будет следующим:

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 123 Игрок второй, при выборе им каждой своей чистой стратегии, гарантировать себе может лишь соответствующий максимальный “проигрыш”, т.е. здесь гарантированные результаты имеют вид

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 124 Очевидно, что для всех i,k

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 125 Теперь очевидно, что первый игрок среди своих гарантированных результатов может выбрать наилучший, т.е. искать или среди гарантированных выигрышей игрок A выбирает наилучший (максимальный) Стратегия игрока А, которой отвечает выигрыш , называется максиминной стратегией (лучшее из худших).

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 126 Игрок В среди гарантированных результатов(максимальных проигрышей) стремится выбрать минимаксную стратегию, обеспечивающую наилучший результат, т.е. наименьший максимальный проигрыш или В стремится получить Стратегия игрока В, которой отвечает проигрыш  называется минимаксной стратегией (тоже для него лучшее из худших).

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 127 Назовем α – нижней ценой игры, а β – верхней ценой игры. Если в игре имеет место α = β, т.е. существует такая стратегия первого игрока Аi0 и стратегия второго игрока Bk0, что , то будем говорить, что игра находится в равновесном состоянии. Элемент платёжной матрицы ai0k0 называется Седловой точкой и очевидно . Нетрудно видеть, что в игре есть седловая точка, тогда и только тогда, когда в платежной матрице есть элемент одновременно минимальный в своей строке и максимальный в своем столбце.

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 128 Итак, если в матричной игре с нулевой суммой существует седловая точка, то максиминная стратегия 1-го игрока и минимаксная стратегия 2-го игрока являются решениями игры. На этих чистых стратегиях достигается компромисс. Пусть игроки уклоняются от своих оптимальных стратегий (при многократном повторении игры). Тогда средний выигрыш игрока А может уменьшаться, а средний проигрыш игрока В может увеличиваться.

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 129 Пример 1. Для следующей платежной матрицы вычисляем гарантированные результаты

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 130 Т.к. здесь седловой точки нет ( ) и игра не имеет решения в классе чистых стратегий. Наилучшие чистые стратегии каждого игрока есть соответственно. Если оба игрока их придерживаются, то наградой, при каждой реализации игры, первому игроку будет не проигрыш (-2), а выигрыш (1), а второму игроку будет не проигрыш (2), а проигрыш меньший и равный той же (1).

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 131 Допустим, что второй игрок знает, что первый игрок осторожный и сначала выберет наилучшую свою чистую стратегию A2, тогда второй игрок решает отойти от своей компромиссной стратегии B2 с желанием улучшить свой результат. Он выбирает стратегию B1: гарантированный выигрыш игрока А есть (-2), т.е. проигрыш (-2), и для В (-2) является выигрышем. Далее, если первый игрок сохраняет свою компромиссную стратегию, второй игрок опять выбирает стратегию В1 и опять выигрывает (- 2), но со временем первый игрок учитывает выбор второго игрока и при дальнейшем повторении игрок А отходит от своей стратегии А2 и выбирает А1, надеясь на прежний выбор второго игрока.

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 132 Пусть так и есть. И мы видим, что при этом, вместо проигрыша (1) у игрока В, в случае выбора им компромиссной стратегии В2, проигрыш игрока В уже составит (4). Этот проигрыш отрезвляет второго игрока и он возвращается к использованию своего наилучшего гарантированного результата, но довольным не является. Ведь он же будет проигрывать. Так ли все мрачно для второго игрока? Можно ли все таки выиграть у первого игрока, или хотя бы не проиграть или на крайний случай свести свой проигрыш к минимуму?

Антагонистические матричные игры двух игроков. Смешенные стратегии. Теорема Дж. фон Неймана. 133 Смешaнные стратегии. Теорема Дж. фон Неймана Итак между нижней и верхней ценой игры может быть большая дистанция, нельзя ли эту разность перераспределить и каждому игроку улучшить свой средний результат при многократном повторении игры за счет использования чистых стратегий с какими то частотностями. Оказывается, что в случае отсутствия седловой точки ( ) компромисс при дележе разности β – α может быть достигнут, если при многократном повторении игры мы будем использовать свои чистые стратегии с некоторыми вероятностями (частотностями), т.к. существует такая частотность применения чистых стратегий для 1-го и 2-го игроков, при которой средний выигрыш 1-го игрока будет больше α, а у 2-го игрока средний проигрыш будет меньше .

Антагонистические матричные игры двух игроков. Смешенные стратегии. Теорема Дж. фон Неймана. 134 Этот набор вероятностей используется для так называемой смешанной стратегии. Образуем вектор Х для 1-го игрока и вектор Y для 2-го игрока где хi – «частота» применений чистой i-той стратегии Ai и yk – «частота» применений чистой k- той стратегии Bk.

Антагонистические матричные игры двух игроков. Смешенные стратегии. Теорема Дж. фон Неймана. 135 При этом очевидно, что Итак X, Y – смешанные стратегии в матричной игре двух лиц. В классе смешанных стратегий средний выигрыш или платежная функция игры имеют вид т.е. средний выигрыш есть взвешенный (вероятностями наступления того или иного выигрыша в классе чистых стратегий) суммарный выигрыш при всех реализациях игры.

Антагонистические матричные игры двух игроков. Смешенные стратегии. Теорема Дж. фон Неймана. 136 Теорема Дж. фон Неймана: Каждая матричная игра с нулевой суммой имеет решение в классе смешанных стратегий, т.е. существуют такие вектора X* и Y*, что Замечание. Согласно теореме решение X* , Y* может быть неединственным и является седловой точкой функции выигрыша и при этом X* есть точка максимина функции , заданной на множестве допустимых векторов Х,Y, а Y* - соответствующая точка минимакса.

Антагонистические матричные игры двух игроков. Сведение матричной игры к задаче ЛП. 137 Сведение матричной игры к задаче ЛП Введем пару взаимосопряженных задач линейного программирования.

Антагонистические матричные игры двух игроков. Сведение матричной игры к задаче ЛП. 138

Антагонистические матричные игры двух игроков. Сведение матричной игры к задаче ЛП. 139

Антагонистические матричные игры двух игроков. Сведение матричной игры к задаче ЛП. 140 Задачи (1) и (2) – двойственные ЗЛП. Оптимальные смешанные стратегии Неймана определяются через решение задач (1) и (2) следующим образом

Антагонистические матричные игры двух игроков. Сведение матричной игры к задаче ЛП. 141 Решение примера 1 на ЭВМ с помощью применения пакета экономических расчетов или других пакетов содержащих симплекс-метод показывает, что оптимальный средний выигрыш первого игрока за игру (или соответственно средний «проигрыш второго игрока») равен 0.5, оптимальная смешанная стратегия первого игрока будет равна Х*·=(0.415;0.585;0), а оптимальная смешанная второго игрока равна Y*·=(0.5;0;0.5).

Антагонистические матричные игры двух игроков. Сведение матричной игры к задаче ЛП. 142 Таким образом первому игроку необходимо примерно в 40% реализаций игры применять первую стратегию, и примерно в 60% - применять вторую стратегию, третью же чистую стратегию вообще не применять. Второму игроку согласно его оптимальной смешанной стратегии надо по очереди, при каждой реализации игры, применять первую или третью чистые стратегии. И таким образом второй игрок снижает свой средний гарантированный проигрыш до 0.5 за игру. Если же первый игрок отклоняется при этом от своей оптимальной смешанной стратегии, то второй игрок и просто выигрывает.

Антагонистические матричные игры двух игроков. Сведение матричной игры к задаче ЛП. 143 Пусть, например, первый игрок в 100 реализациях игры придерживается своей третьей стратегии, т.е. Х··=(0;0;1)Т, а второй - Y* ·= (0.5;0;0.5)Т. Тогда средний «выигрыш» первого игрока за игру приближенно составит –1.5 (0·1·0.5+2·1·0+(-3)·0.5 = 1.5), т.е. первый игрок фактически проигрывает, а второй выигрывает в среднем за игру 1.5. Так что у второго игрока не все так мрачно. Ему необходимо придерживаться своей оптимальной смешанной стратегии и надеяться на неоптимальное поведение первого игрока. При этом, в крайнем случае, если первый игрок не ошибается и использует свою оптимальную смешанную стратегию, то второй игрок будет иметь минимальный средний проигрыш за игру – 0.5.

Антагонистические матричные игры двух игроков. Решение задач в условиях неопределенности и риска. 144 Решение задач в условиях неопределенности и риска На практике смешанные стратегии часто используют при решении так называемых игр с природой. Так, например, оптимальные пропорции выпуска продукции предприятий в условиях неполной информации о спросе можно определить, как оптимальную смешанную стратегию для «игрока», играющего против «природы» (спроса). Приведем пример такой задачи.

Антагонистические матричные игры двух игроков. Решение задач в условиях неопределенности и риска. 145 Задача 2. Предприятие может выпускать три вида продукции (А1, А2, А3), получая при этом прибыль, зависящую от спроса. Спрос в свою очередь может принимать одно из четырех состояний ( В1, В2, В3, В4) - хорошая аналогия с сезонным спросом на товары. В следующей платежной матрице элементы aik характеризуют прибыль, которую получит предприятие при выпуске i-й продукции и k-м состоянии спроса: A =

Антагонистические матричные игры двух игроков. Решение задач в условиях неопределенности и риска. 146 Пусть требуется определить оптимальные пропорции в выпускаемой продукции, считая состояние спроса полностью неопределенным, гарантируя при этом среднюю величину прибыли при любом состоянии спроса. Оптимальная смешанная стратегия (седловой точки тут нет, проверьте!), найденная с помощью сведения игровой задачи к задачам ЛП, имеет вид Х* ·= (0.5;0.5;0)Т, а средний выигрыш равняется 5.

Антагонистические матричные игры двух игроков. Решение задач в условиях неопределенности и риска. 147 Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игроком 1. Игрок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре. Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально, хотя вполне могут встретиться ситуации, в которых «игроком» 2 действительно может быть природа (например, обстоятельства, связанные с погодными условиями или с природными стихийными силами).

Антагонистические матричные игры двух игроков. Решение задач в условиях неопределенности и риска. 148 На первый взгляд отсутствие обдуманного противодействия упрощает игроку задачу выбора решения. Однако, хотя лицу, принимающему решение (ЛПР) никто не мешает, ему труднее обосновать свой выбор, поскольку в этом случае гарантированный результат не известен. Методы принятия решений в играх с природой зависят от характера неопределенности, точнее от того, известны или нет вероятности альтернатив (стратегий) природы, т.е. имеет ли место ситуация риска или неопределенности. Ниже будут описаны методы, применяемые в обоих случаях.

Решение задач в условиях неопределенности и риска. Понятие риска. 149 Понятие риска Пусть игрок 1 имеет m возможных стратегий: а у природы имеется n возможных альтернатив (стратегий): тогда условия игры с природой задаются матрицей выигрышей игрока 1: А =

Решение задач в условиях неопределенности и риска. Понятие риска. 150 Платит, естественно, не «природа», а некая третья сторона (или совокупность сторон, влияющих на принятие решений игроком 1 и объединенных в понятие «природа»). Возможен и другой способ задания матрицы игры с природой: не в виде матрицы выигрышей, а в виде так называемой матрицы рисков R или матрицы упущенных возможностей. Величина риска – это размер платы за отсутствие информации о состоянии среды и при этом матрица R может быть построена непосредственно из условий задачи или на основе матрицы выигрышей A.

Решение задач в условиях неопределенности и риска. Риск игрока. Матрица рисков. 151 Риски(упущенные возможности) игрока Разность между выигрышем, который он получил бы, если бы знал состояние «природы», и выигрышем, который он получит в тех же условиях, применяя ту или иную стратегию. Матрица рисков(упущенных возможностей) Это таблица, в которой заданы стратегии игрока, состояния «природы» и риски при всех возможных сочетаниях стратегий «природы».

Решение задач в условиях неопределенности и риска. Формирование матрицы рисков. 152 Формирование матрицы рисков Зная состояние природы (стратегию) , игрок выбирает ту стратегию, при которой его выигрыш максимальный, т.е. , где при заданном k. Например, для матрицы выигрышей: А=

Решение задач в условиях неопределенности и риска. Формирование матрицы рисков. 153 Согласно введенным определениям и получаем матрицу рисков: R= Независимо от вида матрицы игры требуется выбрать такую стратегию игрока (чистую или смешанную, если последняя имеет смысл), которая была бы наиболее выгодной по сравнению с другими.

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 154 Основные критерии выбора лучшей стратегии В случаях отсутствия информации о вероятностях состояний среды (природы) для определения наилучших решений используются следующие критерии: Максимакса, Вальда, Сэвиджа, Гурвица. Применение каждого из перечисленных критериев проиллюстрируем на примере матрицы выигрышей A или связанной с ней матрицы рисков R.

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 155 Критерий Максимакса С его помощью определяется стратегия, максимизирующая максимальные выигрыши для каждого состояния природы. Это критерий крайнего оптимизма. Наилучшим признается решение, при котором достигается максимальный выигрыш, равный Нетрудно увидеть, что для матрицы A наилучшим решением будет A2, при котором достигается максимальный выигрыш - 8. Следует отметить, что ситуации, требующие применения такого критерия, в экономике в общем нередки, и пользуются им не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение, когда они вынуждены руководствоваться принципом «или пан, или пропал».

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 156 Максиминный критерий Вальда – критерий разумного пессимизма основан на гипотезе о том, что при выборе решения надо рассчитывать на самый худший возможный результат, т.к. здесь природа рассматривается как агрессивно настроенный и разумный противник. Выбирается стратегия на которой достигается наилучший гарантированный результат, т.е. первый игрок действует по принципу максмина и для каждой своей стратегии сначала выбирает наихудший результат, а затем выбирается та из них для которой этот результат наилучший.

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 157 Для платежной матрицы А нетрудно рассчитать: для первой стратегии (i=1) для второй стратегии (i=2) для третьей стратегии(i=3) Тогда , что соответствует второй стратегии А2 игрока 1. В соответствии с критерием Вальда, из всех самых неудачных результатов выбирается лучший (W=3).

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 158 Этот критерий формирует оптимальную стратегию игрока, при которой минимальный выигрыш максимален, т.е. выбирается стратегия, гарантирующая при любых условиях выигрыш, не меньший, чем нижняя цена игры. Это несколько перестраховочная позиция, рассчитанная на худший случай. Такая стратегия приемлема, например, когда игрок не хочет рисковать, или не имеет право рисковать и желает застраховать себя от неожиданных проигрышей. Выбор такой стратегии определяется отношением игрока к риску.

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 159 Критерий минимаксного риска Сэвиджа. Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуя не матрицей выигрышей А, а матрицей рисков R (или матрицей упущенных возможностей, матрицей сожаления): Для матрицы R нетрудно рассчитать: для первой стратегии(i=1) ; для второй стратегии(i=2) ; для третьей стратегии(i=3) .

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 160 Минимально возможный из самых крупных рисков, равный 3, достигается при использовании второй стратегии А2. Итак для критерия Сэвиджа оптимальной считается альтернатива минимизирующая максимальный риск или здесь используется минимаксный критерий для матрицы сожаления и таким образом выбирается стратегия, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации.

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 161 Критерий оптимизма–пессимизма Гурвица. Этот критерий компромиссный и рекомендует при выборе альтернативы в условиях неопределенности не руководствоваться ни крайним пессимизмом, ни крайним оптимизмом. Крайние оценки учитываются с экспертным коэффициентом оптимизма(или, если удобно, пессимизма), выбираемым между нулем и единицей, т.е. критерий при выборе решения рекомендует руководствоваться некоторым «средним» результатом, характеризующим состояние между разумным пессимизмом и безудержным оптимизмом.

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 162 Согласно этому критерию стратегия в матрице А выбирается в соответствии со значением: где здесь p – коэффициент пессимизма При p = 0 критерий Гурвица совпадает с максимаксным критерием, а при p=1 – с критерием Вальда. Покажем процедуру применения данного критерия для матрицы А при p=0,5: для первой стратегии для второй стратегии для третьей стратегии

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 163 Тогда , т.е. оптимальной является вторая стратегия А2. Применительно к матрице рисков R критерий пессимизма – оптимизма Гурвица имеет вид: При p=0 выбор стратегии игрока 1 осуществляется по условию наименьшего из всех возможных рисков при p=1 – по критерию минимаксного риска Сэвиджа.

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 164 Пример: Проиллюстрируем результаты применения рассмотренных выше критериев еще на одном примере матрицы выигрышей: Для игрока 1 лучшими являются альтернативы: по критерию Вальда – А4, по критерию Сэвиджа – А3, по критерию Гурвица (при p=0,6) – А4, по критерию максимакса – А4.

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 165 Поскольку стратегия А4 фигурирует в качестве оптимальной по трем критериям из четырех и поэтому ее можно здесь рекомендовать для применения. Таким образом, в случае отсутствия информации о вероятностях состояний среды выбор критерия проводится эвристическим способом, т.к. математически строгих рекомендаций по выбору критериев принятия решений нет. Это объясняется не слабостью теории, а неопределенностью самой ситуации. Единственный разумный выход в подобных случаях – попытаться получить дополнительную информацию, например, путем проведения исследований или экспериментов.

Решение задач в условиях неопределенности и риска. Основные критерии выбора лучшей стратегии. 166 При отсутствии дополнительной информации принимаемые решения теоретически недостаточно обоснованы и в значительной мере субъективны и в частности, зависят от мнения экспертов. Хотя применение математических методов в играх с природой не дает абсолютно достоверного результата и последний в определенной степени является субъективным (вследствие произвольности выбора критерия принятия решения), использование формальных математических подходов создает некоторое упорядочение имеющихся в распоряжении ЛПР данных и такое упорядочение представлений о проблеме само по себе способствует повышению качества принимаемых решений.

Антагонистические матричные игры двух игроков. Доминирующие стратегии. 167 Доминирующие стратегии Оказывается, что матрицы игр можно упрощать, оперируя смыслом строк и столбцов и исключая заведомо невыигрышные стратегии. Например, рассмотрим матрицу игры

Антагонистические матричные игры двух игроков. Доминирующие стратегии. 168 Здесь очевидно, что при сравнении второй и третьей стратегий первого игрока между собой третья стратегия ей проигрывает, т.к. при любой стратегии второго игрока результаты по второй стратегии не хуже и поэтому первый игрок будет всегда использовать из этих двух стратегий только вторую. При этом говорят, что стратегия А2 доминирует А3 или А2 – доминирующая, а А3 – доминируемая стратегии. Вычеркнем доминируемую стратегию, получим

Антагонистические матричные игры двух игроков. Доминирующие стратегии. 169 Между оставшимися стратегиями первого игрока доминирования уже не наблюдается. Рассмотрим стратегии второго игрока. Здесь, очевидно, что четвертая и третья стратегии(четвертый и третий столбцы матрицы проигрышей) всегда(при любой стратегии первого игрока) хуже (проигрыши больше) первой стратегии второго игрока и поэтому 4 и 3 стратегии второго игрока неэффективны по сравнению с первой его стратегией. Таким образом пришли к существенному упрощению исходной платежной матрицы

Антагонистические матричные игры двух игроков. Решение матричных игр 2*n и m*2 графическим методом. 170 Решение матричных игр 2*n и m*2 графическим методом На примере задачи о фермере продемонстрируем, с одной стороны возможности теории игр при моделировании реальных ситуаций при принятии решений, а с другой – приведем один метод нахождения оптимальных смешанных стратегий для частных классов игр. Здесь будет использоваться теорема из теории матричных игр с нулевой суммой, полезная при практическом решении частных классов игр.

Антагонистические матричные игры двух игроков. Решение матричных игр 2*n и m*2 графическим методом. 171 Теорема об активных стратегиях. Если первый игрок использует свою оптимальную смешанную стратегию Х*, а второй – одну из чистых стратегий, входящую в состав его оптимальной смешанной стратегии Y*·, то средний оптимальный выигрыш v равен линейной комбинации компонент вектора Х*, где коэффициентами линейной комбинации выступают коэффициенты столбца платежной матрицы, отвечающего выбранной чистой стратегии второго игрока, т.е. для всех значений индекса k, которым соответствуют номера чистых стратегий второго игрока, входящих в состав его оптимальной смешанной стратегии.

Антагонистические матричные игры двух игроков. Решение матричных игр 2*n и m*2 графическим методом. 172 Аналогично, если второй игрок использует свою оптимальную смешанную стратегию Y*, а первый – одну из чистых стратегий, входящую в состав его оптимальной смешанной стратегии Х*, то средний оптимальный выигрыш v равен линейной комбинации компонент вектора Y*, где коэффициентами линейной комбинации выступают коэффициенты строки платежной матрицы, отвечающего выбранной чистой стратегии первого игрока, т.е. для всех значений индекса i, которым соответствуют номера чистых стратегий первого игрока, входящих в состав его оптимальной смешанной стратегии Х*.

Задача о фермере. 173 Задача о фермере Каждый год фермер должен принимать решение о посеве на своих площадях (предположим 100 га) традиционных для него (или региона) трех культур в любой пропорции. Фермер аккуратно ведет и анализирует многолетнюю базу данных урожайности этих культур на своих площадях и сочетание основных климатических факторов (количество осадков и средняя температура в летний сезон).

Задача о фермере. 174 Для простоты анализа по фактору «осадки» фермер ввел для летнего сезона три градации: Н – нормальный, З – засушливый, Д – дождливый; а для фактора «температура» - две градации: Н – нормальный, Ж – жаркий. Пусть известна статистика по урожайности культур А,А,А (в центнерах с одного гектара) в зависимости от сочетания природных факторов(табл.1) и предполагаемые рыночные цены реализации этих культур(табл.2). Требуется найти решение о посеве этих культур, максимизирующее предполагаемый рыночный доход.

Задача о фермере. 175

Задача о фермере. 176 Теперь вместо табл.1 построим табл. 3 предполагаемого дохода в тысячах рублей, умножая данные урожайности на соответствующие цены.

Задача о фермере. 177 Таблицу можно рассматривать как соответствующий набор выигрышей в матричной игре с нулевой суммой, где фермер «играет» против природы. Столбцы - отвечают стратегиям второго игрока, различным сочетаниям природных факторов, а строки – стратегиям первого игрока, выбору тех или иных культур. В игре нет седловой точки, т.к. нижняя цена игры равна 9, а верхняя – 15, поэтому решение надо искать в классе смешанных стратегий. Предварительно упростим игру, исключая доминируемые стратегии игроков.

Задача о фермере. 178 Сначала сравниваем стратегии второго игрока. Видим, что набор проигрышей первого столбца лучше набора проигрышей второго столбца, т.е. не превышает, поэтому доминируемой стратегией является вторая и ее надо исключить. Аналогично пятая стратегия второго игрока лучше шестой. В оставшейся части платежной матрицы третья строка уступает первой и поэтому третья стратегия первого игрока исключается. В результате получаем игру 2х4 с платежной матрицей

Задача о фермере. 179 Итак, мы уже понимаем, что третью культуру фермер не будет применять – рискованно, т.е. она неактивная и использоваться не будет, а значит х3=0. Решаем эту игру графическим методом, применяя теорему об активных стратегиях. Пусть х – вероятность выбора стратегии А1, а (1-х) – вероятность выбора стратегии А2. Таким образом, в реальной практике х есть частота применения первой стратегии, выбора первой культуры или какую часть своих площадей фермер занимает первой культурой. Можно подойти иначе. Считаем, что однократная реализация игры есть принятие решения о посеве той или иной культуры на каждом конкретном гектаре.

Задача о фермере. 180 Поэтому х·100 есть число гектаров, засеваемых первой культурой, а (1-х)·100 – второй культурой. В декартовой системе координат строим графики функций , , , , 0

Задача о фермере. 181 Также мы видим, что в оптимальную смешанную стратегию второго игрока входят только две стратегии В1,В5 , остальные стратегии не являются активными и поэтому, используя опять теорему об активных стратегиях для второго игрока получаем v=12y1+21y5, v=15y1+9y5 Находим решение этой системы при v=13.8 и получаем, что y1=0.8; y5=0.2. Итак Х* = (0.4;0.6;0)T, Y* = (0.8;0;0;0;0.2;0)T , v=13.8 .

Задача о фермере. 182 Экономическая интерпретация решения – на 40% площадей необходимо использовать первую культуру, на 60% - вторую и при этом гарантированный доход фермера с гектара при наименее благоприятных погодных условиях составит 13.8 тысяч рублей. Т.к у фермера 100 гектаров, то общий гарантированный доход при «наихудшей погоде» будет приближенно равен 1380 тысяч рублей. Замечание. Почему мы используем слово«приближенно»? Вместо ситуации с бесконечным числом однократных реализаций игры для которой и рассчитываются точные вероятности применения чистых стратегий мы используем всего 100 реализаций(гектаров).

Численные методы безусловной оптимизации первого порядка. Вектор-градиент Градиентом дифференцируемой функции f(x) в точке х0 называется n-мерный вектор f(x0), компоненты которого являются частными производными функции f(х), вычисленными в точке х0, т. е. Этот вектор перпендикулярен к плоскости, проведенной через точку х0 , и касательной к поверхности уровня функции f(x), проходящей через точку х0. В каждой точке такой поверхности функция f(x) принимает одинаковое значение. Приравнивая функцию различным постоянным величинам С0, С1, ... , получим серию поверхностей, характеризующих ее топологию

Антиградиент. Градиентный спуск. Вектор-градиент направлен в сторону наискорейшего возрастания функции в данной точке. Вектор, противоположный градиенту (-f’(х[0])), называется антиградиентом и направлен в сторону наискорейшего убывания функции. В точке минимума градиент функции равен нулю. На свойствах градиента основаны методы первого порядка, называемые также градиентными методами минимизации. Использование этих методов в общем случае позволяет определить точку локального минимума функции. Очевидно, что если нет дополнительной информации, то из начальной точки х0 разумно перейти в точку х1, лежащую в направлении антиградиента или направлении наискорейшего убывания функции. Выбирая в качестве направления спуска антиградиент -f’(х[k]) в точке х[k], получаем итерационный процесс вида В координатной форме этот процесс записывается следующим образом:

Критерий останова В качестве критерия останова итерационного процесса используют либо выполнение условия малости приращения аргумента либо выполнение условия малости градиента Здесь ε и δ - заданные малые положительные величины. Градиентные методы отличаются друг от друга способами выбора величины шага . При методе с постоянным шагом для всех итераций выбирается некоторая постоянная величина шага. Достаточно малый шаг обеспечит убывание функции, т. е. выполнение неравенства Однако это может привести к необходимости проводить неприемлемо большое количество итераций для достижения точки минимума. С другой стороны, слишком большой шаг может вызвать неожиданный рост функции либо привести к колебаниям около точки минимума (зацикливанию). Из-за сложности получения необходимой информации для выбора величины шага методы с постоянным шагом применяются на практике редко. Более экономичны в смысле количества итераций и надежности градиентные методы с переменным шагом.

Метод наискорейшего спуска Этот метод есть модификация метода градиентного спуска. На каждой итерации метода градиентного спуска величина шага выбирается из условия минимума функции f(x) в направлении спуска, т. е. Это условие означает, что движение вдоль антиградиента происходит до тех пор, пока значение функции f(x) убывает. С математической точки зрения на каждой итерации необходимо решать задачу одномерной минимизации по функции .

Матрица Гессе(гессиан) определяется как квадратная матрица вторых частных производных гладкой функции многих переменных. Т.к для гладкой функции смешанные производные функции по одним и тем же переменным равны, то гессиан - симметричная квадратная матрица.

Т.е. Собственные числа любой квадратной матрицы А образуют ее спектр и определяются как нули следующего уравнения Корни этого характеристического уравнения матрицы А, вообще говоря, есть комплексные числа. Они могут быть действительными и различными(матрица с простым спектром), могут быть кратными. Матрица А называется положительно определенной(положительно полуопределенной или неотрицательно определенной), если она симметрична и ее собственные числа положительны (неотрицательны). Для таких матриц используются обозначения

Матрица А называется отрицательно определенной(отрицательно полуопределенной) , если она симметрична и ее собственные числа отрицательны (неположительны). Собственным вектором w матрицы A, отвечающим соответствующему собственному числу λ называется ненулевое решение уравнения Aw=λw. Собственные вектора находятся с точностью до константы. Введенные понятия играют большую роль в приложениях математики.

Угловые(диагональные) миноры - Определители m-го порядка , полученные из А вычеркиванием (n-m)-cтрок и (n-m)-столбцов с одинаковыми номерами называются главными минорами.

Критерий Сильвестра Точка экстремума - точка локального минимума и тогда и только тогда, когда знаки угловых миноров все строго положительны. Точка экстремума - точка локального максимума и тогда и только тогда, когда знаки угловых миноров чередуются, начиная с отрицательного.

Дисретные динамические системы. Основные определения. 192 Дискретные динамические системы. Основные определения Пусть состояние объекта в каждый момент времени описывается набором переменных состояний(фазовыми переменными) – координатами вектора состояний х: i=1,..n, Для дискретных систем время t дискретно Здесь N- число тактов управления (если это число тактов заданное – задача с фиксированным временем).

Дискретные динамические системы. Основные определения. 193 На переменные состояния часто накладываются ограничения, диктуемые особенностью задач, например, ограничения определяются принадлежностью каким-то заданным коридорам, диктуемым безопасной эксплуатацией объекта. Эти ограничения называются фазовыми ограничениями. где G-множество допустимых состояний. Объект управления можно представить в виде схемы с входными и выходными сигналами: На выходе объекта – состояние, на входе – управление u(t).

Дискретные динамические системы. Основные определения. 194 u(t) есть r-мерный вектор Координаты вектора управления - управляющие воздействия могут быть стеснены дополнительными ограничениями, диктуемыми техническими возможностями исполнительных устройств и/или запасами ресурсов. Т.е.

Дискретные динамические системы. Основные определения. 195 Ограничения на управление могут представляться в виде замкнутых областей или открытых. Примеры замкнутых областей Программное управление - законы управления, зависящие только от времени. Синтезирующее управление - управление, зависящее не только от времени, но и от состояния. Последнее часто используется при коррекции программных движений х(t). Отметим, что ограничения на управление могут отсутствовать – классические задачи.

Дискретные динамические системы.Основные определения. 196 Системы с обратной связью Синтезирующее управление формируется обратной связью в объекте.

Дисктретные динамические системы. Основные определения. 197 Переменные наблюдения связаны либо с невозможностью фиксировать значения всех переменных состояния либо с ненадобностью таковой и возможностью управления объекта на основе реально наблюдаемых необходимых величин. В таком случае в данной схеме вводится контур наблюдения. Пусть С – матрица размерности mxn.

Дискретные динамические системы. Основные определения. 198 Модель объекта - это соотношения, которые связывают в каждый момент времени входные воздействия управления и его состояния с одной стороны, а с другой- позволяют предсказывать это состояние в зависимости от времени, если известны при этом управляющие воздействия. Математическая модель объекта управления, в идеале, строится с учетом законов предметной области, описывающих функционирование объекта. Отметим, однако, что на практике часто используют статистические модели (их обобщение нейронные модели), основанные на обработке имеющейся информации в рамках той или иной модели «черного ящика»(1943 год, Норберт Винер), т.е. тогда, когда понимания внутренних механизмов функционирования нет.

Модель дискретной управляемой системы 199 Пусть поведение объекта управления описывается уравнением: х - вектор состояния системы, f - вектор функция, описывающая состояние объекта, и строится на законах предметной области. - начальное состояние объекта (задано) где G-это область ограничений на переменные состояния объекта. u - вектор управления где U - некоторое заданное замкнутое выпуклое множество допустимых значений управления. Модель дискретной управляемой системы x(t+1)=f(t, x(t), u(t)), x(0)=

Модель дискретной управляемой системы 200 Рассмотрим управляемый процесс. Предположим, что управление можно разбить на N шагов, а вектор управления – r-мерный вектор, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему из начального состояния в конечное, представляет собой совокупность r пошаговых управлений. В результате управления система переходит из состояния х(0) в х(N), принадлежащее некоторому целевому множеству GG.

Критерии качества управления 201 Мало просто управлять, необходимо управлять рационально. Критерии, оценивающие переход в целевое множество, зависят от поставленной задачи управления: если задача минимизировать N (минимизируем время перехода объекта из начального состояния в конечное) Задача с незакрепленным временем называется задачей с подвижным правым концом. Сюда же входят задачи быстродействия. Критерии качества управления

Критерий качеста управления 202 Если задача минимизировать затраты на управление, то в критерий вводятся затраты на управление, например слагаемое Критерий называется критерием Майера-Больца. Если φ=0 , тогда это критерий Лагранжа. Если F=0 - критерий Майера.

Задача оптимального управления дискретной системой 203 Заключается в выборе управляющего воздействия u(t) или u(t,x) из множества допустимых, которое переводит систему в целевое множество и при этом минимизирует один из критериев качества управления Майера, Лагранжа, Майера-Больца. Задача оптимального управления дискретной системой

Динамическое программирование 204 Динамическое программирование - есть особый метод оптимизации решений, специально приспособленный к так называемым «многошаговым», или «многоэтапным» операциям. Рассмотрим дискретный управляемый процесс, где уравнения состояния объекта подчиняются следующим соотношениям Здесь N-тактов управления.

Динамическое программирование 205 Итак будем считать, что управление u(t) выбирается из минимума следующего функционала (целевой функции) качества управления: Из уравнения, описывающего состояние объекта, следует, что состояние х(k) системы на k-ом шаге зависит только от предшествующего состояния системы х(k-1) и управления на данном шаге u(k-1) и не зависит от предшествующих состояний и управлений.

Сведения исходной задачи оптимального управления к задаче нелинейного программирования 206 Предположим нам известно управление и соответствующая траектория , которая вычисляется по следующей формуле: Сведение дискретной задачи оптимального управления к задаче нелинейного программирования.

Сведения исходной задачи оптимального управления к задаче нелинейного программирования 207 Тогда критерий качества управления имеет следующий вид: Где - r-мерный вектор, и компоненты этого вектора в каждый момент времени неизвестные.

Сведения исходной задачи оптимального управления к задаче нелинейного программирования 208 Получается, что вместо критерия в исходной задаче мы имеем задачу НЛП Итак, каждая задача дискретного оптимального управления эквивалентна некоторой задаче НЛП, но число переменных при этом велико . Формализация в виде задачи оптимального управления помогает генерировать новые вычислительные конструкции для задач НЛП высокой размерности, учитывающие их специфику, в частности схемы динамического программирования.

Принцип оптимальности Беллмана Принцип оптимальности Беллмана - Часть оптимальной траектории сама является оптимальной траекторией. Рассмотрим графическое изображение оптимальной траектории: оптимальная траектория на всем отрезке времени t=0,1,…,N-1

Принцип оптимальности Беллмана 210 Вместо исходного отрезка рассмотрим теперь отрезок времени t,t+1,…,N-1, т.е его конечную часть. Теперь начальное состояние объекта равно . Пусть на конечной части этого отрезка оптимальная траектория будет . Принцип оптимальности Беллмана говорит о том, что всегда должно совпадать с . Таким образом, Р. Беллман ввел в рассмотрение только такие системы, для которых имеет место принцип оптимальности. К счастью, это подавляющее большинство реальных систем.

Функция Беллмана 211 Под функцией Беллмана в текущий момент времени понимаем минимальное значение критерия качества в текущий момент времени: Если t=0, то Таким образом, значение функции Беллмана S(x,t) определяет минимальную величину функционала для любого начального состояния x(t) в любой момент времени t . Или функция Беллмана совпадает с критерием оптимальности на всем интервале времени Функция Беллмана

Уравнение Беллмана 212 Уравнение Беллмана Ключевым в динамическом программировании является уравнение Беллмана. Оказывается для функции Беллмана можно вывести рекуррентное соотношение: Это рекуррентное соотношение имеет конечное условие

Уравнение Беллмана 213 Замечание: если исходный критерий оптимальности был не на минимум, а на максимум, то в уравнении Беллмана меняется только знак операции. Итак, вычислим значение функции Беллмана при t=N-1: ОБРАТНЫЙ ХОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Уравнение Беллмана 214 В следующий момент времени получаем - найдено на предыдущем шаге. Таким образом, при t=0 значение уравнения Беллмана:

Обратный ход динамического программирования 215 Дойдя до 0 и найдя u(0), мы можем восстановить всю картину оптимального решения. Подставим u(0) в систему мы теперь можем вычислить И так далее. Мы проиллюстрировали решение задачи методом Беллмана. Прямой ход динамического программирования

Пример решения задачи, используя уравнение Беллмана 216 Пример: Распределение инвестиций между предприятиями холдинга, включающего 3 предприятия. Для каждого из них известна функция дохода от вложенных инвестиций. Пусть требуется некоторую сумму из инвестиций M=5 млн. у.е. распределить так, чтобы годовой доход холдинга был максимальным. Для простоты выделяемые инвестиции считаем целочисленными. Пример решения задачи, используя уравнение Беллмана

Пример решения задачи, используя уравнение Беллмана 217

Пример решения задачи, используя уравнение Беллмана 218 Значение, записанное в ячейке с координатами (uk, gi), где k=0,1,..,5 и i=1,..,3 соответствует прибыли полученной i-ым предприятием при вложении в него инвестиций в размере uk. Тогда под хi будем понимать остаток нераспределенных инвестиций для i-го предприятия х1 - остаток инвестиций, который можно распределить первому предприятию или начальный запас инвестиций. - остаток средств, которые можно распределить 2-му предприятию. - остаток средств, которые можно распределить 3-му предприятию

Пример решения задачи, используя уравнение Беллмана 219 Тогда 0≤ u1 ≤ х1 0 ≤ u2 ≤ х2 0 ≤ u3 ≤ х3 Итак, математическая модель нашей задачи

Пример решения задачи, используя уравнение Беллмана 220 Уравнение Беллмана для нашей задачи Решение:

Пример решения задачи, используя уравнение Беллмана 221

Пример решения задачи, используя уравнение Беллмана 222

Пример решения задачи, используя уравнение Беллмана 223 Максимальная прибыль I(u)=10,36 при следующем распределении инвестиций (которые вычисляются обратным ходом): и , тогда . При , тогда При

Непрерывные управляемые процессы 224 Непрерывные управляемые процессы Здесь динамика объекта описывается системами дифференциальных уравнений, например, системами обыкновенных дифференциальных уравнений

Непрерывные управляемые процессы 225 Критерий качества Конечное время T может быть как фиксированным, так и не фиксированным (с подвижным правым концом). Частный случай - это задача быстродействия, где =0, F 1, GT= хT

Непрерывные управляемые процессы 226 Итак, в задаче быстродействия требуется выбрать вектор u(t), принадлежащий (2), такой, что вдоль него решение (1) удовлетворяет в каждый момент времени фазовым ограничениям (3) и при этом в конечный момент времени , то есть ищется допустимое управление, переводящее систему в заданную точку за минимальное время

Задача со свободным правым концом 227 Задача со свободным правым концом Задача Майера Оптимизируется(минимизируется) функция конечного состояния Задача Лагранжа

Необходимое условие оптимальности в задаче Майера - Бойца 228 Наличие ограничений на управления типа замкнутых неравенств резко изменяет характеристики результатов. Например, (2) имеет вид некоторого замкнутого множества, включающего свои граничные точки, в частности, u(t)1, t [0,T]. Вместо классического вариационного исчисления, здесь необходимо применять принцип максимума Понтрягина. Принцип максимума Понтрягина. Для формулировки принципа максимума введем семейство множителей Лагранжа - на каждое дифференциальное уравнение свой множитель а затем введем гамильтониан Необходимое условие оптимальности в задаче Майера - Больца

Необходимое условие оптимальности в задаче Майера - Бойца 229 Вводятся n дополнительных соотношений для множителей Лагранжа, имеющих вид системы обыкновенных дифференциальных уравнений первого порядка с условием на правом конце временного интервала – краевое условие. Далее будем считать, что фазовые ограничения (3) и (4) отсутствуют, т.е. рассматривается задача оптимального управления (1), (2), (5) без дополнительных ограничений на переменные состояния.

Принцип максимума Понтрягина 230 Принцип максимума Понтрягина Пусть u*(t) есть оптимальное управление в задаче (1),(2),(5) и ему соответствует оптимальная траектория х*(t). Этой паре u*(t),х*(t) отвечает множитель Лагранжа *(t) – решение задачи (6). Тогда необходимо должно выполняться следующее условие максимума функции H : При почти всех

Принцип максимума Понтрягина 231 Пример 1.

Принцип максимума Понтрягина 232

Принцип максимума Понтрягина 233 Теперь очевидно, что совокупность всевозможных фазовых траекторий, среди которых есть оптимальная изображена на графике Из критерия оптимальности следует, что претендентами на оптимальную траекторию являются т.к. именно для этих траекторий x(1) наименее отклоняется от 0

Принцип максимума Понтрягина 234 Пример 2.

Принцип максимума Понтрягина 235

Принцип максимума Понтрягина 236

Принцип максимума Понтрягина 237 Вводим гамильтониан Вычисляем максимум H по u -

Класс задач оптимального управления, где правая задача принципа максимума распадается 238 Пусть уравнения движения линейны по состоянию x, т. е. Класс задач оптимального управления, где краевая задача принципа максимума распадается

Класс задач оптимального управления, где правая задача принципа максимума распадается 239 Выпишем гамильтониан задачи (1)-(3): Условие трансверсальности - т.е. множитель Лагранжа ортогонален множеству конечных состояний.

Класс задач оптимального управления, где правая задача принципа максимума распадается 240 (1),(4),(5) - есть краевая задача принципа максимума Понтрягина. Из (4) ψ находится независимо от x и u. Затем из (5) находим управление u и подставляем его в (1) и получаем систему для определения оптимальной траектории x. Итак, краевая задача принципа максимума разбилась на 2 начальные задачи (задачи Коши) и одну задачу оптимизации: Начальная задача (4) - решается в обратном времени. Из задачи конечномерной оптимизации (5) находим u(t). 3. Система (1) - решается в прямом времени (от 0 до Т)

Класс задач оптимального управления, где правая задача принципа максимума распадается 241 Для решения задачи (4) в прямом времени на обычном пакете необходимо сделать в (4) замену независимой переменной τ =T- t (вместо t ввести τ) При t=T ,τ=0 При t=0, τ=T. Таким образом, вместо (4), получаем

Задача линейно-квадратичного оптимального управления. Задача Калмана-Лётова 242 Задача линейно-квадратичного оптимального управления. Задача Калмана-Лётова Оптимальные регуляторы Калмана-Летова. Сначала рассмотрим задачи на конечном промежутке времени. Пусть поведение объекта описывается линейной системой:q

Задача линейно-квадратичного оптимального управления. Задача Калмана-Лётова 243 -квадратичная форма по х, определяемая матрицей Q(t). -квадратичная форма по u, определяемая матрицей R(t). Замечание: - транспонированный вектор х Замечание: (u,Ru) - скалярное произведение векторов. Скалярное произведение векторов а и b, с числом элементов n, определяется по формуле:

Задача линейно-квадратичного оптимального управления. Задача Калмана-Лётова 244 Применим принцип максимума Понтрягина к решению этой задачи. Так как оптимальное управление удовлетворяет принципу максимума, т. е. оптимальное управление необходимо является точкой максимума функции H по u при почти всех t, тo необходимо выполнение условия т.е. получаем

Задача линейно-квадратичного оптимального управления. Задача Калмана-Лётова 245

Задача линейно-квадратичного оптимального управления. Задача Калмана-Лётова 246 В данной краевой задаче можно применить метод прогонки (часть координат решения краевой задачи можно записать через другую) или (t)= -К(t)x(t) (**) Подставим (**) в (*).

Задача линейно-квадратичного оптимального управления. Задача Калмана-Лётова 247 Получаем для матрицы К(t) матричную начальную задачу (7) С дополнительным условием в конечный момент Т К(T)=F (8) Задача (7)-(8) является матричной дифференциальной задачей Коши для определения матрицы K(t). Если эту задачу решить, найти K(t) и подставить в (4),то мы получим выражение

Задача линейно-квадратичного оптимального управления. Задача Калмана-Лётова 248 (9) Т. е. управление подозрительное на оптимум определяется в виде явной зависимости от траектории x. (9) - формула синтеза, какое бы ни было состояние х в момент времени t, оптимальное управление в этот момент нам известно, если будет заранее известна матрица K(t). Матрица K(t)-решение задачи (7)-(8) играет большую роль в теории управления - матрица коэффициентов усиления в оптимальном контуре обратной связи.

Задача линейно-квадратичного оптимального управления. Задача Калмана-Лётова 249 Это уравнение (7)-(8) встречается в разных приложениях, в частности при расчетах оптимального движения в условиях случайных помех при белом шуме. Мы рассматриваем задачу на конечном времени с точки зрения инженерной коррекции движения объекта, и формирования соответствующих законов управления. Большой интерес имеют стационарные линейно-квадратичные задачи на полуоси.

Стационарные линейно-квадратичные задачи на полуоси 250 Это задачи следующего типа: Стационарные линейно-квадратичные задачи на полуоси

Стационарные линейно-квадратичные задачи на полуоси 251 Оптимальный регулятор имеет то же выражение И оптимальный синтез в виде (9) можно записать в следующем виде: где K- матричное решение уже не дифференциального уравнения, а алгебраического. (*) Определение. Система управляема на отрезке времени [0,T], если для любого начального и конечного состояний существует кусочно-непрерывное управление, переводящее систему на этом отрезке из начального состояния в конечное.

Стационарные линейно-квадратичные задачи на полуоси 252 Оказывается уравнение (*) разрешимо и его решение K*>0 , если система управляема и Q>0. Система управляема <=> когда ранг матрицы где n - это максимальная размерность невырожденного минора. Итак

Стационарные линейно-квадратичные задачи на полуоси 253 Уравнение (**) называется замкнутой системой для оптимальных движений. Матрица (A-SK) замкнутой системы оказывается обладает замечательным свойством: Собственные числа Reλ(A-SK) (где K>0 - положительно определенное решение алгебраического уравнения Риккати) находятся в левой полуплоскости, т.е. Reλ(A-SK)<0

Стационарные линейно-квадратичные задачи на полуоси 254 Таким образом оптимальное синтезирующее управление в задаче на полуоси делает замкнутую систему асимптотически устойчивой по Ляпунову, т.е. для вcех траекторий замкнутой системы и для любого начального условия выполняется следующее: Или какое бы ни было начальное отклонение системы оптимальное управление стабилизирует систему и возвращает ее в положение равновесия. Итак, теория оптимального управления позволяет находить обратную связь, не просто погашающую отклонение, но и выполняющее это демпфирование оптимальным образом.

0. Устойчивость непрерывных систем Рассмотрим нелинейную систему Дадим определения устойчивости и асимптотической устойчивости заданной траектории x(t). Можно показать, что задача анализа устойчивости заданной траектории x(t) сводится к задаче анализа устойчивости тривиальной траектории x(t). И для тривиальной траектории x(t)0 (f(0,t)0) введем определения Определение 1. Систему (1) будем называть устойчивой в момент времени t0, если для любого ε ≥ 0 существует δ(ε, t0) ≥ 0 такое, что для любой траектории x(t) из условия ║x(t0)║  δ cледует ║x(t)║  ε при t ≥ t0. Определение 2. Систему (1) будем называть асимптотически устойчивой в момент времени t0, если (1) просто устойчивая система и существует h(t0) 0 такое, что для любой траектории x(t) из условия║x(t0)║ ≤ h cледует = 0.

Анализ устойчивости линейных систем по собственным числам матрицы системы Рассмотрим линейную стационарную систему Для асимптотической устойчивости линейной стационарной системы необходимо и достаточно, чтобы все собственные числа матрицы А имели отрицательные действительные части. т.к. .

Принцип максимума Понтрягина для дискретных многошаговых систем управления 257 Принцип максимума Понтрягина для дискретных многошаговых систем управления Пусть уравнение объекта имеет вид x(k+1)=f(x(k),u(k),k) (1) (2) k - дискретное время, k=0,1,…,N-1 (3)

Принцип максимума Понтрягина для дискретных многошаговых систем управления 258 Требуется выбрать управление из (3),так чтобы вдоль траекторий системы (1)-(2) минимизировать функционал (4) Задача (1)-(4) аналог непрерывной задачи Майера-Больца. Принцип максимума для такой задачи имеет некоторые особенности: для произвольной дискретной задачи он не справедлив, т.е. если мы введем аналог гамильтониана, то не всегда оптимальное управление есть точка максимума по u этого гамильтониана.

Принцип максимума Понтрягина для дискретных многошаговых систем управления 259 Теорема (принцип максимума для дискретных систем): Пусть U выпуклое множество, F,φ - непрерывно дифференцируемые функции, а F выпукла по u. Замечание 1. Функция f(x) выпукла по x,если

Принцип максимума Понтрягина для дискретных многошаговых систем управления 260 Или функция выпукла, если она подобна параболе с ветвями вверх, либо прямой. Тогда оптимальное управления задачи (1)-(4) удовлетворяет принципу максимума, т. е. Где - отвечающие оптимальному управлению траектория и соответствующая сопряженная переменная.

Принцип максимума Понтрягина для дискретных многошаговых систем управления 261 Пример: двухшаговая система k=0,1 x(k+1)=x(k)+u(k), x(0)=3

Принцип максимума Понтрягина для дискретных многошаговых систем управления 262

Принцип максимума Понтрягина для дискретных многошаговых систем управления 263

Итак оптимальное управление оптимальная траектория минимальное значение функционала

Введение в ТПР 265 Еще раз концептуально о ТПР Исследование операций; Технологии принятия решений. Исследование операций рассматривает чётко формализованные модели и конкретные количественные методы их исследования (линейное, нелинейное программирование, теории оптимального управления).

Введение в ТПР 266 Технологии принятия решений рассматривают задачи, не имеющие строгих формализованных постановок. Существуют субъективные (неформализуемые) категории - мнение эксперта. Также к Технологиям принятия решений относятся и количественные технологии, к изучению которых мы переходим. Одна из проблем ТПР – множественность целей, критериев оценки (анализа тех или иных альтернатив).

Введение в ТПР 267 Пусть x є Gx - набор альтернатив и имеется I1(x)…Im(x) – m-критериев для сравнения альтернатив. Будем считать, что все эти критерии на max. max Ii(x)= x є Gx Будeм считать argmax Im(x)=

Введение в ТПР. Свертка критериев 268 Множество критериев порождают зачастую субъективность при сравнении. Человек принимающий решение не может оперировать множеством признаков, критериев и естественно упрощает задачу многокритериальную и сводит множество критериев к одному. Этот приём носит название свёртки критериев. Вместо m критериев вводится один: сi - веса ( частные производные свёртки по i-ому критерию), т.е. сi показывает вклад i-ого критерия в общий критерий F(x) или сi - чувствительность F(x) к частному критерию. Чем чувствительность выше, тем критерий важнее.

Введение в ТПР. Свертка критериев 269 Процедура определения весов – есть процесс ранжирования и сама по себе есть отдельная проблема. Чаще всего она решается экспертно, и в этом случае предъявляются требования к экспертам: их суждения не должны сильно отличаться между собой (тогда группа экспертов качественная ). эксперты должны быть независимыми и опытными. Формирование таких экспертных групп возможно только для дорогих кампаний и проектов.

Введение в ТПР. Использование контрольных показателей. 270 Использование контрольных показателей Пусть известна для каждого критерия некая нормативная величина. Определим отношение каждого критерия к своему нормативу, просматривая эти отношения для всех альтернатив и для каждого критерия. Затем определим - критерий наихудший из m критериев, он очень близок к нормативу. Мы выбрали критические направления, теперь ищем c тем чтобы найти альтернативу х, которая отодвигает нас максимально от норматива по наихудшему критерию.

Введение в ТПР. Последовательный метод линейной свертки 271 Это частный случай свертки критериев, когда некоторое сi =1 , а сk =0 и k=1,..,m (ik). Результат такой свёртки – выбор одного главного критерия среди m-критериев. Любой из перечисленных приёмов уязвим для критики и в этой ситуации хотелось бы увидеть критерии с разных сторон сравнивая их между собой. Каждой альтернативе х из Gx отвечает точка в m- мерном пространстве критериев. Метод главного критерия

Введение в ТПР. Свертка критериев в пространстве 272 Метод идеальной точки Предположим, что нам известны по каждому из критериев наилучшие альтернативы и соответствующие наилучшие значения всех критериев при однокритериальном подходе. Введём положительно-определённую матрицу R для взвешивания квадратов отклонений всех критериев от своих наилучших значений.

Введение в ТПР. Свертка критериев в пространстве. 273 Составим общий критерий: введём - вектор текущих критериев. Введем критерий

Паретооптимальные (эффективные) решения 274 Парето-оптимальные (эффективные) решения В. Парето предложил свой подход определения лучших альтернатив по многим критериям сразу. Пусть имеем набор альтернатив х и m критериев оценки альтернатив fi (x), i є [1,..,m] Требуется найти такие альтернативы на которых одновременно (!!!!????) максимизируется m- критериев.

Паретооптимальные (эффективные) решения 275 Вообще говоря, как мы уже отмечали, эта задача не разрешима. Можно лишь найти некий вектор x, который в каком-то другом смысле решает эту задачу. Будем считать вектор оптимальным по Парето (эффективным по Парето), если не существует такого, что fi ( ) ≥ fi ( ), i є 1,.,m и при этом хотя бы одно неравенство строгое fi ( ) > fi ( ) Т.е. Парето - оптимальный вектор х* является неулучшаемым, хотя бы по одному критерию.

Паретооптимальные (эффективные) решения. 276 Пример №1: Спортивная гимнастика среди мужчин ( 6 дисциплин-критериев, 6 чемпионов по видам). Множество претендентов – все участники. Все участники участвуют во всех дисциплинах. В каждой дисциплине выбирается победитель. Группа из 6 чемпионов по всем видам образует Парето множество, т.к. каждый элемент этого множества спортсменов не является улучшаемым, т.к. среди всех спортсменов не найдётся участников, которые имеют результаты по всем дисциплинам не хуже, а хотя бы по одной дисциплине имеют результат лучше.

Паретооптимальные (эффективные) решения 277 Пример № 2: Пусть имеется 2 критерия по отбору банков: f1-доходность f2- надёжность Найдём Парето множество на этом множестве всех банков.

Паретооптимальные (эффективные) решения 278 В этой задаче иллюстрируется популярный подход проекции на плоскость 2-х критериев, реальных многокритериальных множеств. Обозначим точками совокупность банков, координаты которых –это заданные значения оценок по критериям f1 и f2 Банки, принадлежащие северо-восточной границе множества, несравнимы. Банк B уступает банку А по критерию f1, но превосходит по f2. Банк B неулучшаем - в нашем множестве (не найдётся банка, у которого характеристики не хуже, а хотя бы по одному критерию лучше). Банки A, B, C, D, E, (СБ) F принадлежат Парето множеству. Таким образом при выборе банка мы будем оперировать границей A-F , а уже потом на этом множестве естественно склоняться к выбору банков со «средними» характеристиками.

Антагонистические матричные игры двух игроков. Гарантирующие стратегии. 279 Предположим, что на плоскости 2-х критериев, граница множества вариантов имеет следующий вид: Найдём Парето множество на этом множестве.

Принцип оптимальности Неша 280 Выбор по Парето обладает несомненными очевидными преимуществами (неулучшаемость). Однако, при небольшом «шевелении» данных решение задачи может сильно измениться. Но так как в реальности точного ничего нет, а все приближённо, то желательно иметь выбор устойчивый к возмущениям. Принцип устойчивого выбора– выбор альтернативы должен быть устойчивым к возмущениям. При учете этого принципа выбор может сильно измениться. Джон Нэш предложил определение устойчивого выбора. Устойчивый выбор по Нэшу cвязан с образованием коалиций. Принцип оптимальности Нэша

Принцип оптимальности Неша 281 Определение. Пусть на некотором множестве альтернатив имеется выбор

Устойчивость равновесия Нэша Равновесие по Нэшу говорит, что одному игроку не выгодно отклоняться от согласованного решения. Это условие устойчивости компромисса. Т.е. условие устойчивости компромисса заключается в том, что, если существует коалиция и она держится соглашения, то тот один, кто нарушает – проигрывает. Но не всякий компромисс устойчив и не всякий оптимальный выбор по Парето устойчивый по Нэшу и наоборот не всякое устойчивое равновесие по Нэшу эффективно по Парето.

Принцип оптимальности Неша. Пример Гермермера 283 Пример (Гермейера) Пусть N – игроков, N - критериев тогда выигрыш каждого fi=1. Итак, здесь все игроки получают по выигрышу равном единице. Оказывается такое решение является оптимальным по Нэшу. Действительно

Принцип оптимальности Неша. Пример Гермермера 284 Пусть, например, второй игрок отклоняется от оптимального соглашения и выбирает Остальные игроки придерживаются соглашения и выигрывают по (1+дельта). А выигрыш второго игрока уменьшается и составляет 1-δ, т.е. меньше своего выигрыша, когда он придерживался соглашения и выбирал Итак, при малых положительных δ для предложенной альтернативы выполняется условие оптимальности по Нэшу. Но эта альтернатива неэффективна по Парето. Действительно

Принцип оптимальности Неша. Пример Гермермера 285 Возьмём . Тогда выигрыш каждого будет равен fi =N-1, т.е. последняя альтернатива является лучшей сразу по всем критериям, чем предыдущее решение, а значит не эффективно по Парето. Пусть теперь все игроки, кроме Одного, придерживаются стратегии , а один отклоняется и, например, тогда для j-го игрока выигрыш составит Выигрыш других игроков будет равен Т.е. решение неулучшаемо или эффективно по Парето, но это решение не устойчиво по Нэшу – один вышел из соглашения и все проиграли.

Принцип оптимальности Неша. Пример Гермера 286 Итак решение устойчиво по Нэшу, но не эффективно по Парето. А решение оптимально по Парето, но не устойчиво по Нэшу. Системы принятия решений, где равновесие одновременно оптимально по Парето и устойчиво по Нэшу – встречаются достаточно редко. Для этого необходим некий объединяющий критерий для игроков.

Теорема Гермейра-Вателя 287 Теорема Гермейера-Вателя Пусть имеется общий глобальный критерий для N субъектов и каждый из них имеет свой критерий: - это часть ресурса направляемая i –м игроком на свои интересы, - часть ресурса , который i -ый субъект направляет на общие цели.

Теорема Гермейра-Вателя 288 - связывающий критерий, который определяет эффективность расходования средств «из общего котла». Теорема. Если f и F монотонно возрастающие функции, тогда существуют устойчивые равновесия, среди которых, по крайней мере, одно эффективно по Парето. Вывод: Анализируя интересы группы взаимодействующих субъектов, желательно выделить критерии каждого, формализуя их в виде монотонно возрастающих функций, и при этом обязательно находить связывающий критерий.

Методы принятия решений в многокритериальной среде 289 Методы принятия решений в многокритериальной среде Метод анализа иерархии (МАИ). Метод Flectrе Метод вербального анализа MVA. При рассмотрении многокритериальной задачи важное место занимают шкалы измерений, в которых мы будем производить сравнения различных альтернатив, критериев. Предполагаем, что для всех альтернатив мы можем определить интенсивности, определяемые выбранными критериями.

290 Типы шкал и их основные характеристики.

291

292

293

294

Задача многокритериальной теории принятия решений 295 Задача многокритериальной теории принятия решений характеризуется следующим набором данных, представляемые следующим кортежем. Он записывается в виде: T – постановка задачи, тип задачи. S – множество альтернатив. K – множество критериев. X – множество шкал. F – отображение множества альтернатив на множество векторных оценок. P – система предпочтений лица, принимающего решение R – решающее правило.

Задача многокритериальной теории принятия решений 296 Процесс принятия решения должен учитывать как достаточно формализуемые этапы и несколько нечёткие (субъективные). Более точно - все приведённые параметры кортежа включают в себя стратегии неопределённости, субъективность и в итоге Вы ищете решение на основе несколько размытых представлений. Противовес размытости, нечёткости - опыт, знание, интуиция экспертов, с одной стороны, а с другой - и сама процедура принятия решений, предусматривающая процедуры осреднения.

Задача многокритериальной теории принятия решений 297 Несмотря на неопределённость на всех этапах, некоторые из них достаточно детерминированные, например, постановка задачи. Очень важно альтернативы соотнести с целями. К – множество критериев(допустим есть критерий – максимум прибыли, но нет согласия в коллективе; укрепить коллектив только деньгами нельзя – должно быть что-то вроде социальной гармонии и соответствующий критерий по гармонии???!!!). Х – множество шкал. Желательно проводить выбор в нескольких шкалах, «победитель» – лидер по многим шкалам одновременно . F – отображение. Р – система предпочтений.

Метод анализа иерархий Метод анализа иерархий Метод анализа иерархий предполагает декомпозицию проблемы на простые составляющие части и обработку суждений лица принимающего решение. В результате определяется относительная значимость исследуемых альтернатив для всех критериев, находящихся в иерархии. Относительная значимость выражается численно в виде векторов приоритетов. Полученные таким образом значения векторов являются оценками в шкале отношений и соответствуют так называемым жестким оценкам.

Постановка задачи, решаемой с помощью метода анализа иерархий, заключается обычно в следующем: Дано: общая цель решения задачи; критерии оценки альтернатив; альтернативы. Требуется: выбрать наилучшую альтернативу. Подход метода анализа иерархий состоит из совокупности этапов:

Структуризация задачи в виде иерархической структуры с несколькими уровнями: цели-критерии-альтернативы. Попарное сравнение элементов каждого уровня лицом, принимающим решения. Результаты сравнения имеют числовой характер. Вычисление коэффициентов важности(предпочтения) для элементов каждого уровня. Проверка согласованности суждений ЛПР. Подсчет количественной оценки качества альтернатив. Выбор лучшей альтернативы.

Структуризация задачи в виде иерархии Построение иерархий начинается с очерчивания проблемы исследования. Далее строится иерархия, включающая цель на верхнем уровне, промежуточные уровни (например, критерии) и альтернативы, формирующие самый нижний иерархический уровень.

Обратно симметричные матрицы При формировании парных сравнений используются Обратно симметричные матрицы. показывает оценку сравнения i-ого с j-ым. Свойства: Максимальное по модулю значение собственного числа в обратносимметричных матрицах ≥ размерности матрицы n. Положительная обратносимметричная матрица согласованна тогда и только тогда, когда максимальное значение собственного числа равно размеру матрицы n.

Важное значение имеет согласованность матрицы парных сравнений (т.е. следование логике экспертов при простановке оценок). Для оценки согласованности матрицы вводится понятие индекса согласованности. Uo – индекс однородности Uc –индекс согласованности - максимальное по значению собственное число Oc – оценка согласованности Oo – оценка однородности M(uo) – среднее значение индекса согласованности для случайно сгенерированной матрицы размерности n.

Шкала отношений Для логического построения матрицы парных сравнений применяется шкала отношений.

Пример: Выбор сотового оператора из трех альтернатив (Билайн, Мегафон, МТС) по следующим критерием: Тарифы Услуги Качество Цена Решение:

Иерархия: Уровень выбора оператора сотовой связи Уровень критериев Уровень альтернатив Решение Сначала построим матрицы парных сравнений при сравнении альтернатив с точки зрения каждого из критериев, затем сравним критерии между собой. Для полученных матриц парных сравнений посчитаем λmax и нормированные собственные вектора, отвечающие λmax . Вычислим все индексы и построим итоговые оценки при помощи иерархического синтеза

Вывод Исходя из произведенных расчетов, выбранный оператор сотовой связи - МЕГАФОН. Данный вывод основан на мнении эксперта со следующими параметрами: место проживания и пользования услугами сотовой связи – Москва и Московская область возраст – 20 лет безработный.