ДИСКРЕТНАЯ МАТЕМАТИКА С.130-134,134 -143 ДМ 2. Теория формальных



















































116-2011_!l13_dm_kob_minim.ppt
- Количество слайдов: 74
 ДИСКРЕТНАЯ МАТЕМАТИКА
ДИСКРЕТНАЯ МАТЕМАТИКА

 С.130-134,134 -143
С.130-134,134 -143
 ДМ 2. Теория формальных языков и автоматов. Тема 4. Логические автоматы Тема 5.Тестирование логических автоматов Тема 6. Элементы теории кодирования Тема 7. Автоматы и формальные языки
ДМ 2. Теория формальных языков и автоматов. Тема 4. Логические автоматы Тема 5.Тестирование логических автоматов Тема 6. Элементы теории кодирования Тема 7. Автоматы и формальные языки
 Т7.Автоматы, и формальные языки
Т7.Автоматы, и формальные языки
 Регулярные языки и конечные автоматы
Регулярные языки и конечные автоматы
 Множество всех слов, распознаваемых автоматом, мы назвали языком.
Множество всех слов, распознаваемых автоматом, мы назвали языком.
 Автоматный язык Грамматика типа 3 – имеют правила вида АaB, либо Ab, где А,ВN; a,bT. Здесь A,B,a,b – одиночные символы (не цепочки) соответствующих словарей. A,B - состояния автомата, a,b - входные символы
Автоматный язык Грамматика типа 3 – имеют правила вида АaB, либо Ab, где А,ВN; a,bT. Здесь A,B,a,b – одиночные символы (не цепочки) соответствующих словарей. A,B - состояния автомата, a,b - входные символы
 Суммой языков L и L´ называется язык, который обозначается L + L´ и получается объединением множеств L и L´, т.е. L + L´ = Сумма языков состоит из слов, принадлежащих хотя бы одному из языков L и L´. Поэтому L + L´ = L´ + L . .
Суммой языков L и L´ называется язык, который обозначается L + L´ и получается объединением множеств L и L´, т.е. L + L´ = Сумма языков состоит из слов, принадлежащих хотя бы одному из языков L и L´. Поэтому L + L´ = L´ + L . .
 Далее конкатенацией (или соединением) слов w и w´ будем называть слово ww´, полученное приписываем справа слова w´ к слову w. Например, конкатенацией слов ba и cba будет слово bacba. Из этих же слов можно получить слово cbaba, которое является конкатенацией cba и ba. В общем случае конкатенации ww´ и w´w различаются. .
Далее конкатенацией (или соединением) слов w и w´ будем называть слово ww´, полученное приписываем справа слова w´ к слову w. Например, конкатенацией слов ba и cba будет слово bacba. Из этих же слов можно получить слово cbaba, которое является конкатенацией cba и ba. В общем случае конкатенации ww´ и w´w различаются. .
 Произведением языков L и L´ называется язык, который обозначается L·L´ и получается в результате конкатенации всех возможных слов w и w´, где w принадлежит языку L, а w´ – языку L´, Пример 1. Пусть L = {a, cb}, L´ = {ab, bсb}. Тогда L·L´ = {aab, abcb, cbab, cbbcb}, L´·L = {aba, abcb, bcba, bcbcb}. Слово abcb принадлежит обоим языкам L·L´ и L´·L.
Произведением языков L и L´ называется язык, который обозначается L·L´ и получается в результате конкатенации всех возможных слов w и w´, где w принадлежит языку L, а w´ – языку L´, Пример 1. Пусть L = {a, cb}, L´ = {ab, bсb}. Тогда L·L´ = {aab, abcb, cbab, cbbcb}, L´·L = {aba, abcb, bcba, bcbcb}. Слово abcb принадлежит обоим языкам L·L´ и L´·L.
 Итерацией языка L называется язык, который обозначается L* и получается в результате сложения бесконечного числа языков
Итерацией языка L называется язык, который обозначается L* и получается в результате сложения бесконечного числа языков
 Пусть имеется алфавит А = {а1, а2, …, аs}. Одноэлементные языки а1, а2, …, аs, а также язык, содержащий только пустое слово Λ, будем называть элементарными языками.
Пусть имеется алфавит А = {а1, а2, …, аs}. Одноэлементные языки а1, а2, …, аs, а также язык, содержащий только пустое слово Λ, будем называть элементарными языками.
 Регулярным языком называется такой язык, который можно получить из элементарных языков с помощью конечного числа операций сложения, умножения и итерации.
Регулярным языком называется такой язык, который можно получить из элементарных языков с помощью конечного числа операций сложения, умножения и итерации.
 Пусть автомат с начальным состоянием v1 и заключительным состоянием v3 задан графом Язык L можно задать регулярным выражением b·(a + b)* + a·b*·а·(a + b)*
Пусть автомат с начальным состоянием v1 и заключительным состоянием v3 задан графом Язык L можно задать регулярным выражением b·(a + b)* + a·b*·а·(a + b)*
 ТЕОРЕМА КЛИНИ (основная теорема теории автоматов). Язык L распознается конечным детерминированным автоматом тогда и только тогда, когда L – регулярный язык.
ТЕОРЕМА КЛИНИ (основная теорема теории автоматов). Язык L распознается конечным детерминированным автоматом тогда и только тогда, когда L – регулярный язык.
 Stephen C Kleene-1909-1994. США.
Stephen C Kleene-1909-1994. США.
 Хомский, Аврам Ноам
Хомский, Аврам Ноам
 Это теоретическая основа многих информационных технологий, таких как разработка математического обеспечения вычислительных систем, проектирование компиляторов и синтаксических анализаторов для языков программирования, создание лингвистических структур для баз данных и знаний
Это теоретическая основа многих информационных технологий, таких как разработка математического обеспечения вычислительных систем, проектирование компиляторов и синтаксических анализаторов для языков программирования, создание лингвистических структур для баз данных и знаний
 Понятие о задании автомата сетью Петри
Понятие о задании автомата сетью Петри
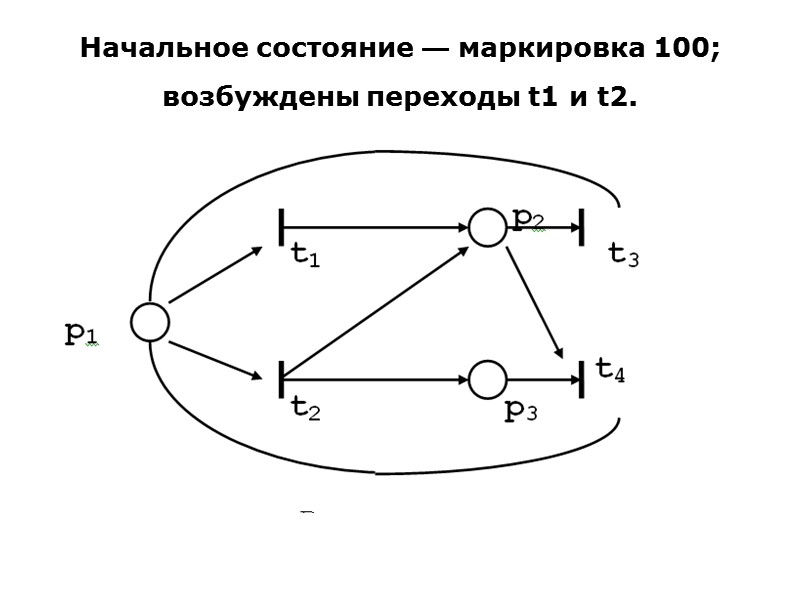
 Начальное состояние — маркировка 100; возбуждены переходы t1 и t2.
Начальное состояние — маркировка 100; возбуждены переходы t1 и t2.
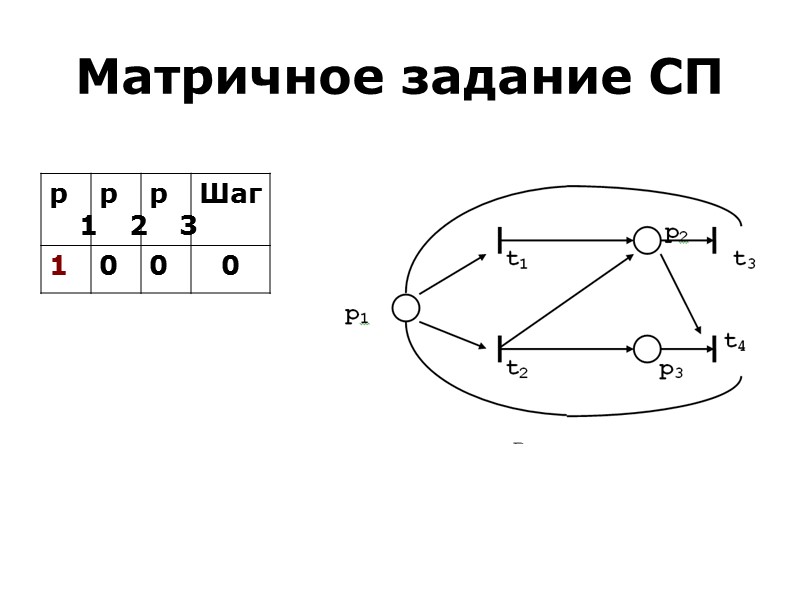
 Матричное задание СП
Матричное задание СП
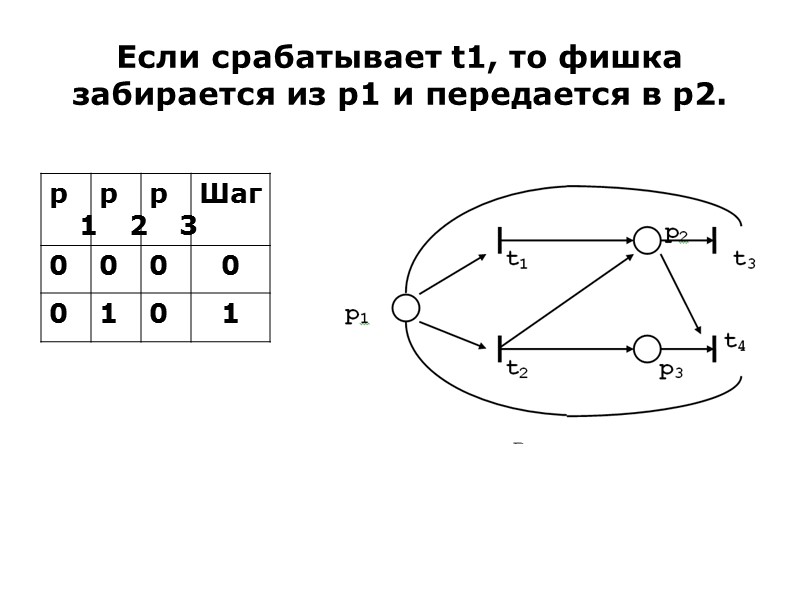
 Если срабатывает t1, то фишка забирается из р1 и передается в р2.
Если срабатывает t1, то фишка забирается из р1 и передается в р2.
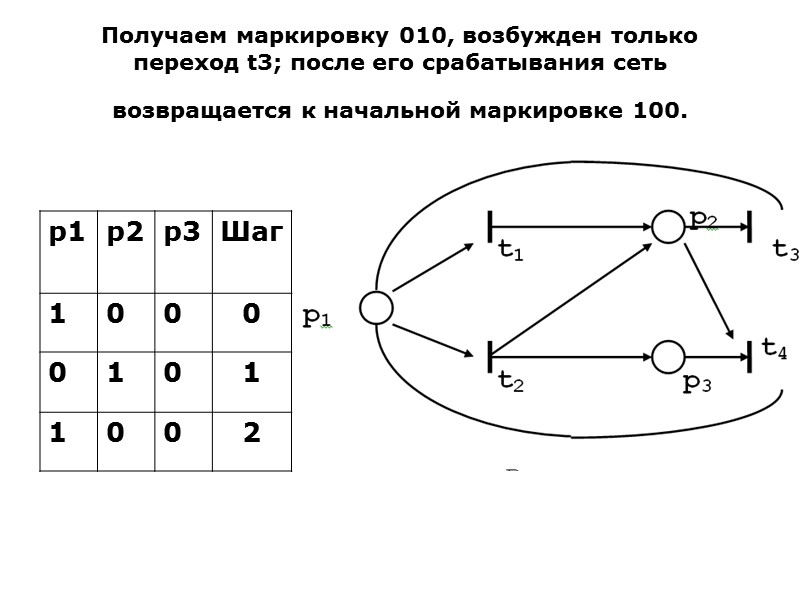
 Получаем маркировку 010, возбужден только переход t3; после его срабатывания сеть возвращается к начальной маркировке 100.
Получаем маркировку 010, возбужден только переход t3; после его срабатывания сеть возвращается к начальной маркировке 100.
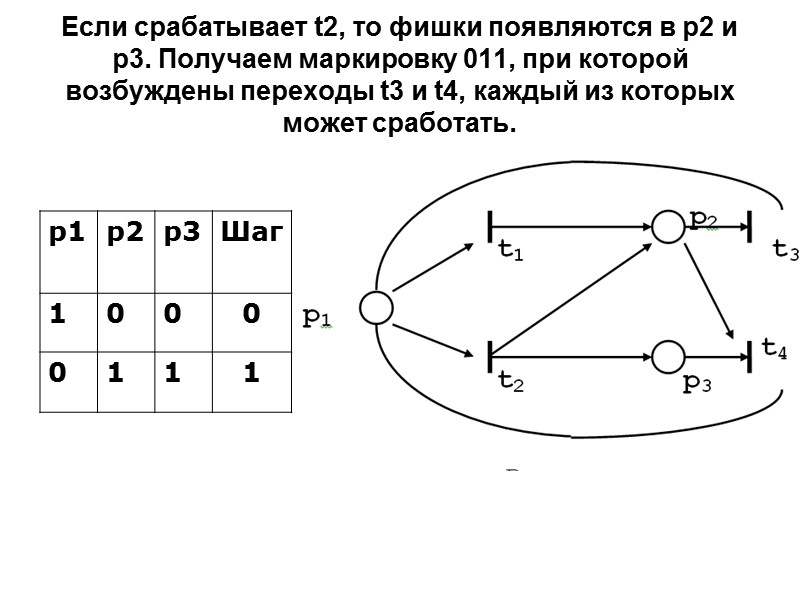
 Если срабатывает t2, то фишки появляются в р2 и р3. Получаем маркировку 011, при которой возбуждены переходы t3 и t4, каждый из которых может сработать.
Если срабатывает t2, то фишки появляются в р2 и р3. Получаем маркировку 011, при которой возбуждены переходы t3 и t4, каждый из которых может сработать.
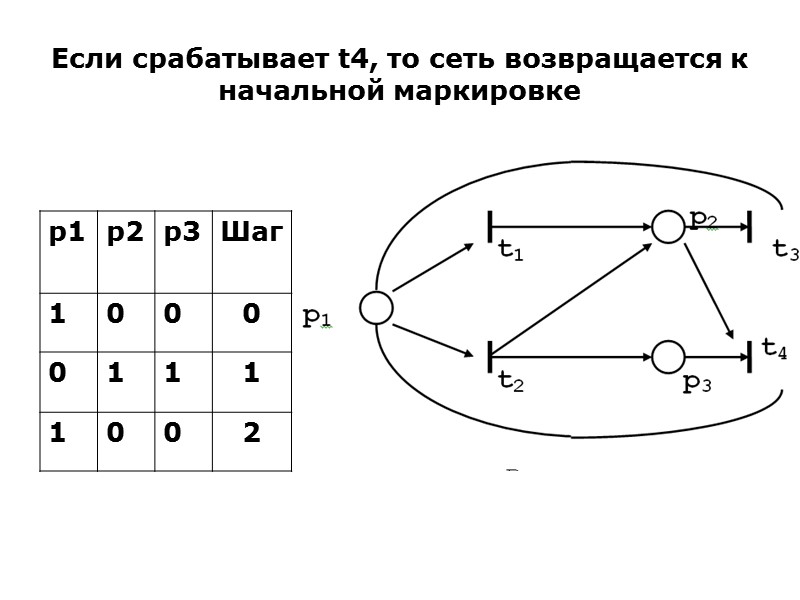
 Если срабатывает t4, то сеть возвращается к начальной маркировке
Если срабатывает t4, то сеть возвращается к начальной маркировке
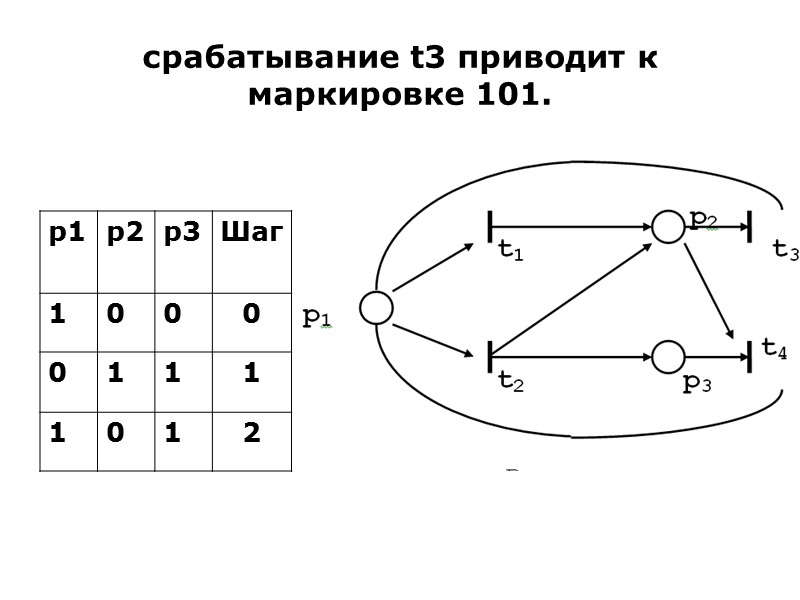
 срабатывание t3 приводит к маркировке 101.
срабатывание t3 приводит к маркировке 101.
 Магазинный автомат
Магазинный автомат
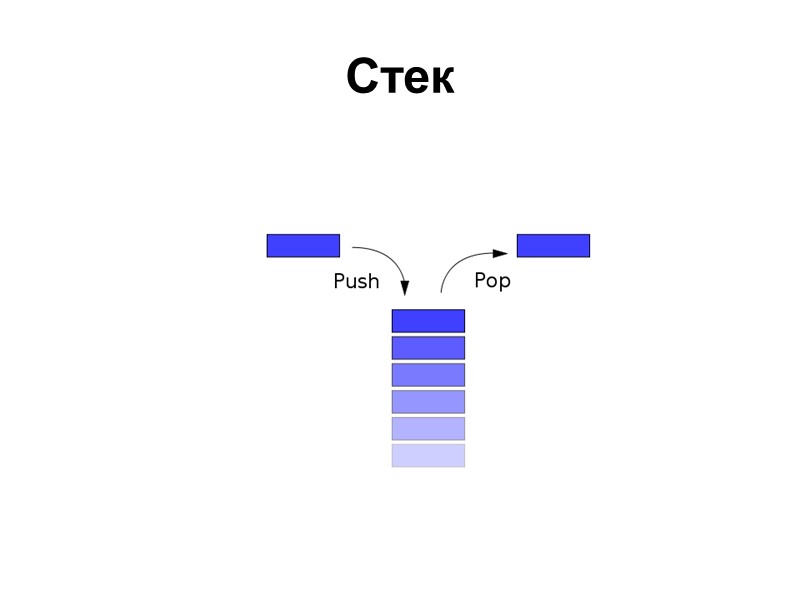
 Магазин - стек Стек (англ. stack — стопка) — структура данных с методом доступа к элементам LIFO (англ. Last In — First Out, «последним пришел — первым вышел»). Стек - магазин - по аналогии с магазином в огнестрельном оружии (стрельба начнётся с патрона, заряженного последним
Магазин - стек Стек (англ. stack — стопка) — структура данных с методом доступа к элементам LIFO (англ. Last In — First Out, «последним пришел — первым вышел»). Стек - магазин - по аналогии с магазином в огнестрельном оружии (стрельба начнётся с патрона, заряженного последним
 Стек
Стек
 Стеки широко используются в вычислительной технике — так для отслеживания точек возврата из подпрограмм стек вызовов, который является неотъемлемой частью архитектуры большинства современных процессоров.
Стеки широко используются в вычислительной технике — так для отслеживания точек возврата из подпрограмм стек вызовов, который является неотъемлемой частью архитектуры большинства современных процессоров.
 Языки программирования высокого уровня используют стек вызовов для передачи параметров при вызове процедур.
Языки программирования высокого уровня используют стек вызовов для передачи параметров при вызове процедур.
 Стек FIFO First In First Out
Стек FIFO First In First Out
 Лекция 13
Лекция 13
 Эквивалентность автоматов. Теорема Мура
Эквивалентность автоматов. Теорема Мура
 Автоматы А и В
Автоматы А и В
 Их реакции на входную цепочку aabbabb одинаковы:
Их реакции на входную цепочку aabbabb одинаковы:
 Эквиваленты ли эти автоматы? Перебрать все входные цепочки невозможно – их бесконечно много.
Эквиваленты ли эти автоматы? Перебрать все входные цепочки невозможно – их бесконечно много.
 Поэтому проблема эквивалентности автоматов нетривиальна. К счастью, существует метод решения этой проблемы. Он основан на понятии прямого произведения автоматов.
Поэтому проблема эквивалентности автоматов нетривиальна. К счастью, существует метод решения этой проблемы. Он основан на понятии прямого произведения автоматов.
 Теорема Мура.
Теорема Мура.
 Теорема Мура. Два конечных автомата с одинаковым входным алфавитом эквивалентны тогда и только тогда, когда для любого достижимого состояния в их прямом произведении А × В функции выходов одинаковы:
Теорема Мура. Два конечных автомата с одинаковым входным алфавитом эквивалентны тогда и только тогда, когда для любого достижимого состояния в их прямом произведении А × В функции выходов одинаковы:
 Два конечных автомата с одинаковым входным алфавитом эквивалентны тогда и только тогда, когда для любого достижимого состояния в их прямом произведении А × В функции выходов одинаковы:
Два конечных автомата с одинаковым входным алфавитом эквивалентны тогда и только тогда, когда для любого достижимого состояния в их прямом произведении А × В функции выходов одинаковы:
 Параллельно работающие на одном входе автоматы
Параллельно работающие на одном входе автоматы
 Граф прямого произведения автоматов А и В - автомат А × В
Граф прямого произведения автоматов А и В - автомат А × В
 Удалим недостижимые состояния
Удалим недостижимые состояния
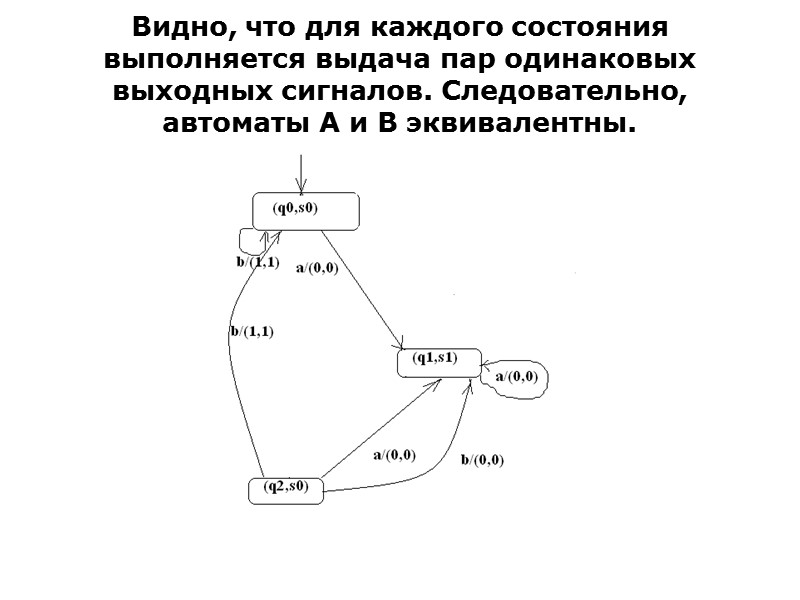
 Видно, что для каждого состояния выполняется выдача пар одинаковых выходных сигналов. Следовательно, автоматы А и В эквивалентны.
Видно, что для каждого состояния выполняется выдача пар одинаковых выходных сигналов. Следовательно, автоматы А и В эквивалентны.
 Минимизация автоматов
Минимизация автоматов
 Минимизация конечных автоматов Разные автоматы могут функционировать одинаково, даже если у них разное число состояний. Важной задачей теории автоматов является нахождение минимального автомата, реализующего заданное автоматное отображение.
Минимизация конечных автоматов Разные автоматы могут функционировать одинаково, даже если у них разное число состояний. Важной задачей теории автоматов является нахождение минимального автомата, реализующего заданное автоматное отображение.

 Начальное разбиение – это один блок, включающий все состояния: 0= {А0 <1,2,3,4,5,6,7,8,9>}.
Начальное разбиение – это один блок, включающий все состояния: 0= {А0 <1,2,3,4,5,6,7,8,9>}.
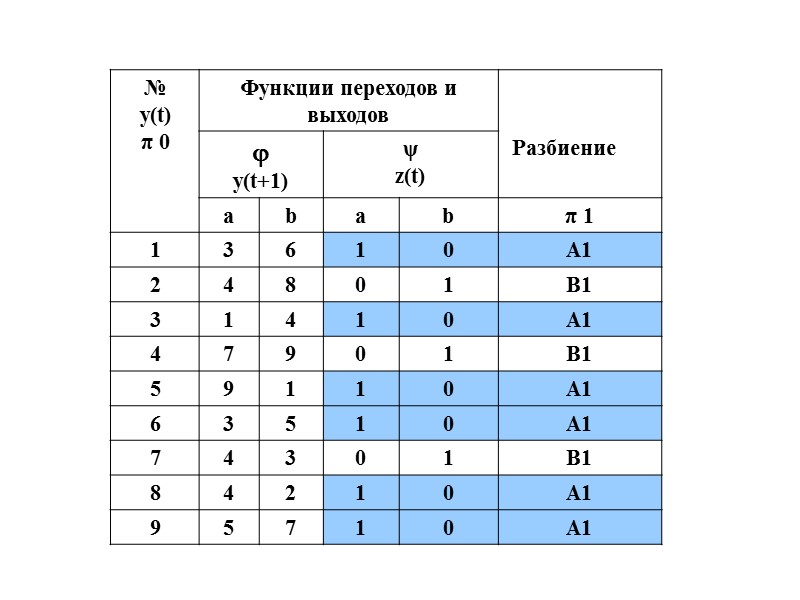
 Строим 1 – те состояния, которые не различаются цепочкой длины 1 – то есть символом либо а, либо b. Видим, что состояния разбиваются на два блока – в первом реакции 1,0, во втором – 0,1: 1= {А1=<1,3,5,6,8,9>;В1=<2,4,7>}
Строим 1 – те состояния, которые не различаются цепочкой длины 1 – то есть символом либо а, либо b. Видим, что состояния разбиваются на два блока – в первом реакции 1,0, во втором – 0,1: 1= {А1=<1,3,5,6,8,9>;В1=<2,4,7>}

 Теперь смотрим, в какие блоки переходит автомат из блоков 1 под воздействием символов а, либо b.
Теперь смотрим, в какие блоки переходит автомат из блоков 1 под воздействием символов а, либо b.
 Итак, в первой строчке под воздействием «а» осуществляется переход в состояние 3 – это блок А1, под воздействием «b» осуществляется переход в состояние 6, это тоже блок А1. Так и записываем. π 1= {А1 = <1,3,5,6,8,9>; В1=<2,4,7>}.
Итак, в первой строчке под воздействием «а» осуществляется переход в состояние 3 – это блок А1, под воздействием «b» осуществляется переход в состояние 6, это тоже блок А1. Так и записываем. π 1= {А1 = <1,3,5,6,8,9>; В1=<2,4,7>}.
 Во второй строчке под воздействием «а» осуществляется переход в состояние 4 – это блок В1, под воздействием «b» осуществляется переход в состояние 6, это блок А1. π 1= {А1 = <1,3,5,6,8,9>; В1=<2,4,7>}.
Во второй строчке под воздействием «а» осуществляется переход в состояние 4 – это блок В1, под воздействием «b» осуществляется переход в состояние 6, это блок А1. π 1= {А1 = <1,3,5,6,8,9>; В1=<2,4,7>}.
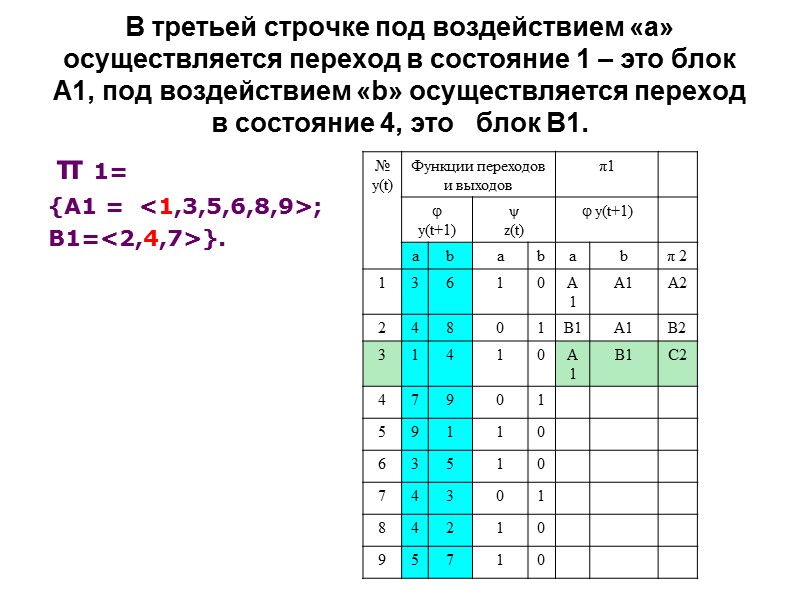
 В третьей строчке под воздействием «а» осуществляется переход в состояние 1 – это блок А1, под воздействием «b» осуществляется переход в состояние 4, это блок В1. π 1= {А1 = <1,3,5,6,8,9>; В1=<2,4,7>}.
В третьей строчке под воздействием «а» осуществляется переход в состояние 1 – это блок А1, под воздействием «b» осуществляется переход в состояние 4, это блок В1. π 1= {А1 = <1,3,5,6,8,9>; В1=<2,4,7>}.
 В четвёртой строчке под воздействием «а» осуществляется переход в состояние 7 – это блок В1, под воздействием «b» осуществляется переход в состояние 9, это блок А1. Действуя аналогично, получаем всю таблицу π 1= {А1 = <1,3,5,6,8,9>; В1=<2,4,7>}.
В четвёртой строчке под воздействием «а» осуществляется переход в состояние 7 – это блок В1, под воздействием «b» осуществляется переход в состояние 9, это блок А1. Действуя аналогично, получаем всю таблицу π 1= {А1 = <1,3,5,6,8,9>; В1=<2,4,7>}.
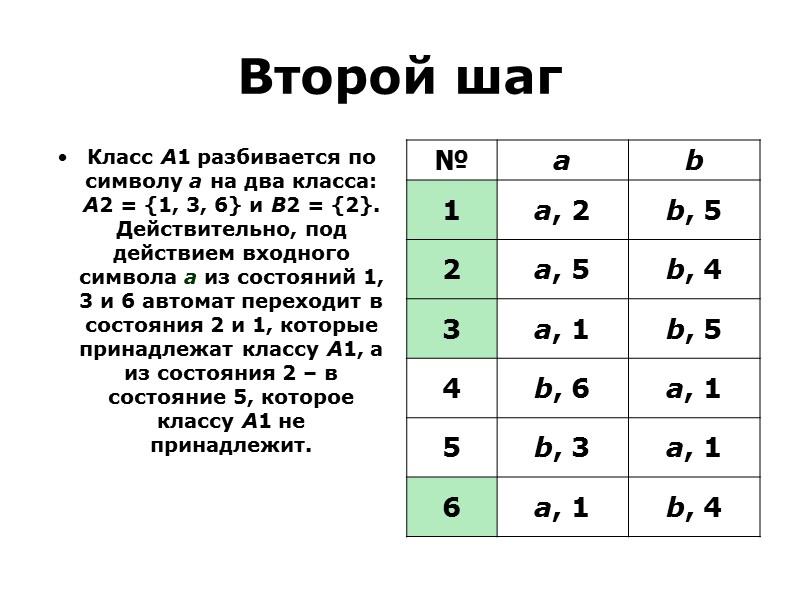
 Получили π2 = {А2 = <1,5,6>;В2=<2,4,7>; С2=<3,9>; D2=<8>}.
Получили π2 = {А2 = <1,5,6>;В2=<2,4,7>; С2=<3,9>; D2=<8>}.
 Строим π3. При его построении уже не нужно анализировать, в какой блок π2 переходит автомат из состояния 8, поскольку оно единственное в π2 и дальше дробиться не будет. π2 = {А2 = <1,5,6>; В2=<2,4,7>; С2=<3,9>; D2=<8>}.
Строим π3. При его построении уже не нужно анализировать, в какой блок π2 переходит автомат из состояния 8, поскольку оно единственное в π2 и дальше дробиться не будет. π2 = {А2 = <1,5,6>; В2=<2,4,7>; С2=<3,9>; D2=<8>}.
 Получаем разбиение π3= {А3 = <1,5,6>; В3=<2>; С3=<4,7>; D 3=<3,9>; Е3=<8>}. π2 = {А2 = <1,5,6>; В2=<2,4,7>; С2=<3,9>; D2=<8>}.
Получаем разбиение π3= {А3 = <1,5,6>; В3=<2>; С3=<4,7>; D 3=<3,9>; Е3=<8>}. π2 = {А2 = <1,5,6>; В2=<2,4,7>; С2=<3,9>; D2=<8>}.
 Строим π4
Строим π4
 Получаем разбиение π4= {А4 = <1,5,6>; В4=<2>; С4=<4,7>; D 4=<3,9>; Е4=<8>}. Поскольку π4 = π3, искомое разбиение найдено. Минимальный автомат имеет 5 состояний, а его функции переходов и выходов определяются так (берём за основу разбиение π3): (А3,а)= D3, ψ (А3,а)=1 и так далее.
Получаем разбиение π4= {А4 = <1,5,6>; В4=<2>; С4=<4,7>; D 4=<3,9>; Е4=<8>}. Поскольку π4 = π3, искомое разбиение найдено. Минимальный автомат имеет 5 состояний, а его функции переходов и выходов определяются так (берём за основу разбиение π3): (А3,а)= D3, ψ (А3,а)=1 и так далее.

