Дискретная математика Презентации к курсу лекций Структура

Дискретная математика Презентации к курсу лекций

Структура курса • Теория множеств • Логика • Теория графов

Литература • Общая – 1. Новиков Ф. А. Дискретная математика для программистов. 2000, 304 с. – 2. Донской В. И. Дискретная математика. 2000. – 3. Яблонский С. В. Введение в дискретную математику. Серия: Высшая математика. М. : Высшая школа. 2000 – 4. Москинова Г. И. Дискретная математика. Математика для менеджеров в примерах и упражнениях: Учебное пособие. М. : ИК Логос. 2000. – 5. Акимов О. Е. Дискретная математика. Логика, группы, графы. Серия: Технический университет. М. : Лаборатория Базовых Знаний. 2001. – 6. Иванов Б. Н. Дискретная математика. Алгоритмы и программы. Серия: Технический университет. М. : Лаборатория Базовых Знаний. 2001 г, 285 с. – 7. Ахо А. В. , Хопфорт Д. Э. , Ульман Д. Д. Структуры данных и алгоритмы

Литература • Теория множеств – Коршунов Ю. М. Математические основы кибернетики. Учебное пособие для втузов. М. : Энергия. 1972, 376 с. – Кузнецов О. П. , Адельсон-Вельский Г. М. Дискретная математика для инженера. М. : Энергоатомиздат, 1988. 480 с. – Основы кибернетики. Математические основы кибернетики. Под ред. проф. К. А. Пупкова. М: Высшая школа. 1974. 413 с. – П. С. Александров Введение в теорию множеств и общую топологию М. : Наука, 1977 – Н. Бурбаки Начала математики. Первая часть. Основные структуры анализа. Книга первая. Теория множеств М. : , Мир, 1965. 456 с – К. Куратовский, А. Мостовский Теория множеств М. : , Мир, 1970. 416 с – Дж. Барвайс Справочная книга по математической логике в четырёх частях под редакцией. Часть II. Теория множеств М. : , Наука, 1982. 376 с

Литература • Логика – Бочаров В. А. , Маркин В. И. Основы логики. 1997. – Савельев А. Я. Арифметические и логические основы цифровых автоматов: Учебник. - М. : Высш. школа, 1980. - 255 с. , ил. – Савельев А. Я. Прикладная теория цифровых автоматов: Учебник. - М. : Высш. школа, 1989. - 273 с. , ил. – Теория автоматов / Ю. Г. Карпов - СПб. : Питер, 2002. - 224 с.

Литература • Теория графов – Зыков А. А. Основы теории графов. 1987. 384 с. – Оре О. Теория графов. М: Наука, 1980. 336 с – Цой С. , Цхай С. М. Прикладная теория графов. Алма-Ата: Наука, 1971. 500 c. – Лекции по теории графов / Емеличев В. А. и др. - М. : Наука, 1990. - 384 с.

Теория множеств • • • Множества Операции над множествами Упорядоченные множества Соответствия Отображения и функции Отношения

Множество. Основные понятия • Множество – некоторая совокупность объектов или элементов. • Элемент множества отдельный объект множества. • Конечные множества можно задавать перечислением их элементов. При перечислении элементов множества можно использовать характеристически свойства.

Способы задания множеств • Перечисление элементов М = {a 1, a 2, a 3, …, ak} M 9 = {1, 2, 3, 4, 5, 6, 7, 8, 9} • Выделение определяющего свойства M = {x | P(x)} M 9 = {n | n & n < 10} • Определение порождающей процедуры M = {x | x = f} M 9 = {n | for n from 1 to 9 write n}

Парадокс Рассела • Множество всех множеств, не содержащих себя в качестве элемента: Y = {X | X X} Если множество Y существует, то Y Y ? Пусть Y Y , тогда Y Y (по определению) Пусть Y Y, тогда Y Y (по определению) Получаем логическое противоречие.

Сравнение множеств • Два множества равны между собой, они состоят из одних и тех же элементов если – Свойства: для любых трех множеств X, Y, Z верно • рефлексивность X = X; • коммутативность • транзитивность X = Y Y = X; (X = Y) & (Y = Z) X = Z. (идемпотентность) • Множество X является подмножеством множества Y, если любой элемент множества X принадлежит и множеству Y. X Y, если x X и x Y; – Свойства: X Y, если X Y • рефлексивность X X • транзитивность X Y & Y Z, X Z • свойства 0 и 1 Y U

Универсум и пустое множество • Пустое множество, обозначаемое или {} есть множество, не содержащее элементов • Универсальное множество или универсум есть множество, элементами которого являются все возможные элементы множества.

Операции над множествами • Объединение A B = {x |x A x B} • Пересечение A B = {x |x A & x B} • Разность AB = {x |x A & x B} • Симметрическая разность A/B = (A B)(A B ) = {x | (x A & x B)} • Дополнение = {x | x A} = UA, где U - некоторый универсум.

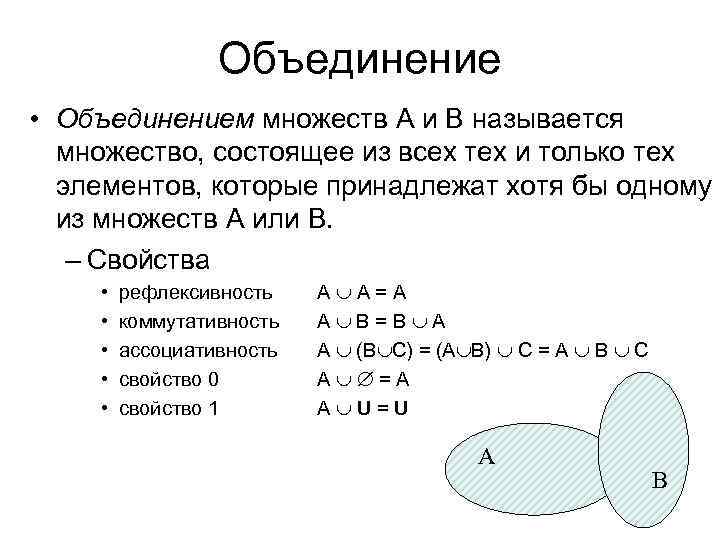Объединение • Объединением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В. – Свойства • • • рефлексивность коммутативность ассоциативность свойство 0 свойство 1 А А=A А В=В А А (В С) = (А В) С = А В С А =А А U=U А В

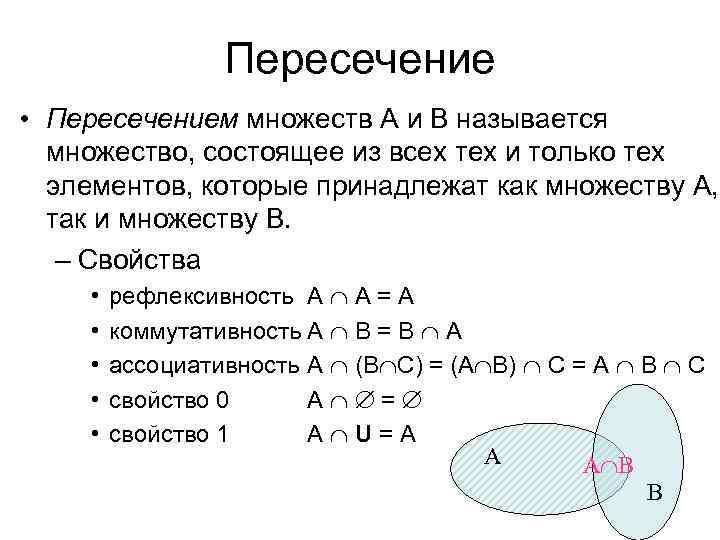Пересечение • Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству А, так и множеству В. – Свойства • • • рефлексивность А А = A коммутативность А В = В А ассоциативность А (В С) = (А В) С = А В С свойство 0 А = свойство 1 А U=А А А В В

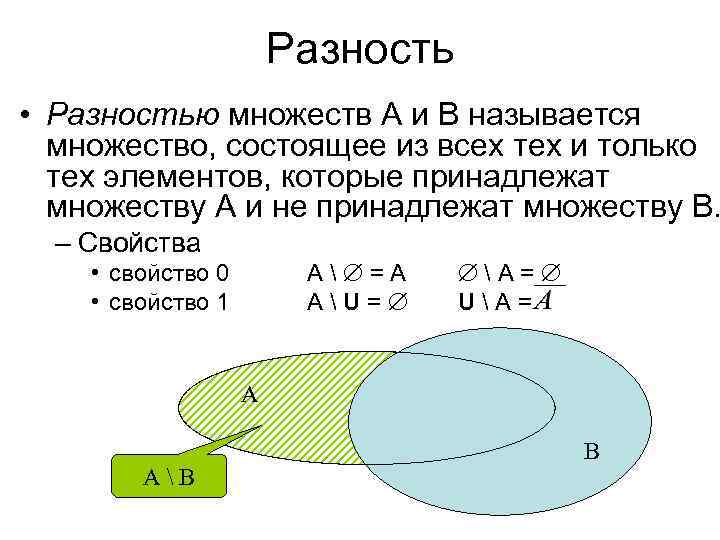Разность • Разностью множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В. – Свойства А =А АU= • свойство 0 • свойство 1 А= UА= А АВ В

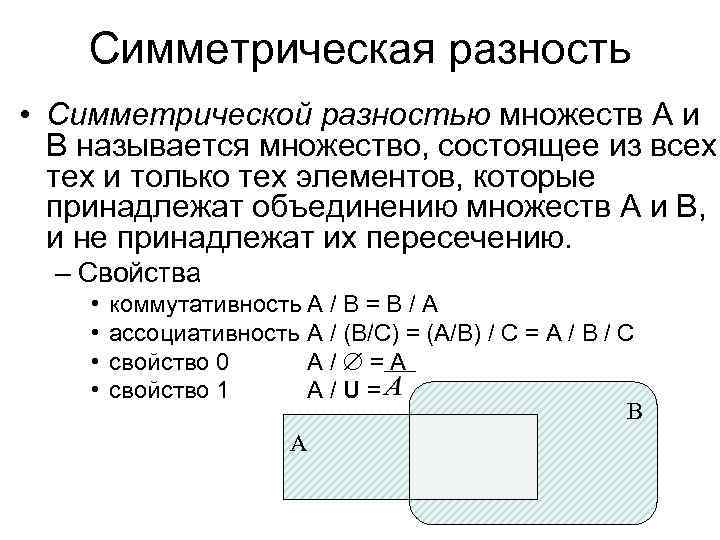Симметрическая разность • Симметрической разностью множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат объединению множеств А и В, и не принадлежат их пересечению. – Свойства • • коммутативность А / В = В / А ассоциативность А / (В/С) = (А/В) / С = А / В / С свойство 0 А/ =А свойство 1 А/U= В А

Законы теории множеств • Дистрибутивный – A (B C) = (A B) (A C) • Закон поглощения – (A B) A = A • Законы де Моргана – • Выражение для разности –AB=A

Декартово произведение множеств, булеан, мощность множества • Булеаном множества А называется множество всех подмножества А и обозначается как P(А) • Декартовым произведением множеств А и В называется множество, определяемое следующим образом: А В = {(a, b) | a A & b B}. Объект (a, b) называется упорядоченной парой. • Мощность множества |M| количество элементов множества

Степень множества • Степенью множества А называется его прямое произведение самого на себя: Аn = A A. . . A. n раз Соответственно, А 0 = { }; А 1 = A; А 2 = A A; • Теорема: Теорема |A B| = |A| |B|. Аn = A An-1.

Проекция множества • Пусть А - множество, состоящее из кортежей длины n, тогда проекцией множества А называют множество проекций кортежей из А. (операция проекции может применяться только к таким множествам, элементами которых являются кортежи одинаковой длины). – Если А = X Y, то Пр1 А = Х, Пр2 А = Y. – Если А X Y, то Пр1 А Х, Пр2 А Y.

Соответствия • Соответствие - это множество пар вида (a, b), образующихся при сопоставлении заданным образом элементов множества А элементам множества В, и сами сопоставляемые множества А и В. q = (A, B, Q), Q A B. – Пр. АQ A называется областью определения соответствия, или источником соответствия. – Пр. ВQ В называется областью значений соответствия, или приемником. – Множество пар Q, определяющих соответствие, называется графиком соответствия.

Способы задания соответствия • В виде описания в соответствии с определением А={красный, желтый, зеленый}; B={стоять, идти}; А Q={(красный, стоять), (зелёный, идти)} • Графически • В виде матрицы B

Обратное соответствие • Соответствие, обозначаемое как q-1 = (B, A, Q-1), где Q-1 B A, является обратным для соответствия q=(A, B, Q), где Q A B, и получается, если данное соответствие q рассматривать в обратном направлении. – Пример: А={красный, желтый, зеленый}; B={стоять, идти}; Q={(красный, стоять), (зеленый, идти)}. Q-1={(стоять, красный), (идти, зеленый)}. – Свойства: (q-1)-1 = q.

Композиция соответствий • Композиция соответствий - это операция с 3 -мя множествами А, В, С, на которых заданы два соответствия q = (A, B, Q), где Q A B и р = (В, С, Р), где Р B C, причем область значений первого соответствия q совпадает с областью определения второго р Пр2 Q = Пр1 Р. • Обозначение: q(p) = (A, C, Q P), Q P A C.

Отображения • Полностью определенное на множестве источнике соответствие q(A, B, Q) (где множество А есть область определения данного соответствия q) называется отображением множества А в множество В. • Обозначения – Г: А В = (А, В, Г), где Г А В, Пр. АГ = А или (А, В, Г), Г А В | a A b B • Каждому элементу x A отображение Г ставит в соответствие подмножество Г(x) В, которое называют образом элемента x. • Пусть X A; x X, Г(x) В – образ элемента х, тогда Г(Х) = – образ множества Х

Отображения • Отображение i : X X называется тождественным, если I(x) = x для всех х Х, и обозначается как id. X или как 1 Х. Свойство: Для любого отображения Г : X Y имеет место 1 Y g = g 1 X = g. • Отображение Г : X Y называется инъекцией, если для любых 2 -х x 1, x 2 X из равенства Г(x 1)=Г(x 2) следует x 1=x 2. • Отображение Г : X Y называется сюръекцией, если для каждого y Y существует такой x X, что y=Г(x). • Отображение Г : X Y называется биекцией, если оно одновременно является инъекцией и сюръекцией.

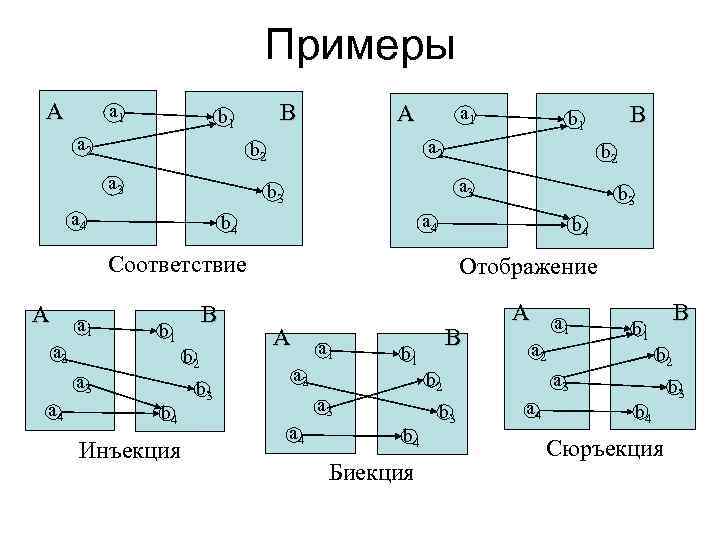Примеры А а 1 В b 1 а 2 А b 2 а 3 b 3 а 4 b 4 Соответствие А а 1 а 2 b 1 b 2 а 3 а 4 В b 4 Инъекция b 3 а 4 b 4 В b 1 а 2 b 2 а 3 а 1 Отображение А а 1 а 2 b 2 а 3 а 4 В b 1 А а 1 b 4 Биекция b 3 В b 1 b 2 а 3 а 4 b 4 Сюръекция b 3

Свойства отображений • Если Х 1 А и Х 2 А, то – верно только в случае однозначного отображения.

Частный случай отображения • Отображение вида Г: А А является частным случаем отображения Г: А В, при А=В, представляет собой отображение множества А в себя самого и определяется парой (А, Г), где Г А 2. • Композицией 2 -х отображений вида Г: А А и : А А называется отображение Г , определяемое как (Г )(х) = Г( (х)). • Если Г= , то Г 2(х)=Г(Г(х)), Г 3(х)=Г(Г 2(х)), … Гn(х)=Г(Гn-1(х)); Г 0(х)=Г(Г-1(х))=(ГГ-1)(х)=x

Функции • Однозначное отображение f: X Y называется функцией. Однозначность означает, что для любых пар (x 1, y 1) f и (x 2, y 2) f из x 1 = x 2 следует y 1 = y 2. • Если Y R, то функция f называется функцией с вещественными значениями. • Для любых пар (x, y) f y = f(x). • Формальное определение f = { (x, y) X Y | y = f(x) }

Способы задания функций • Перечисление пар (х, у) • Формула преобразования х в у • График функции

Функции многих переменных • Если в выражении f: X Y Х=U V, то имеем функцию 2 -х переменных f(u, v), где u U, v V. • Или формально f = { (u, v, y) U V Y | y = f(u, v) } • Функция n переменных f = { (x 1, x 2, …, xn, y) X 1 X 2 … Xn Y | y = f(x 1, x 2, …, xn) }

Операции над функциями • Обратная функция f-1: Y X • Композиция функций если f: X Y, g: Y Z, то f g: X Z z = (f g)(x) = g(f(x))

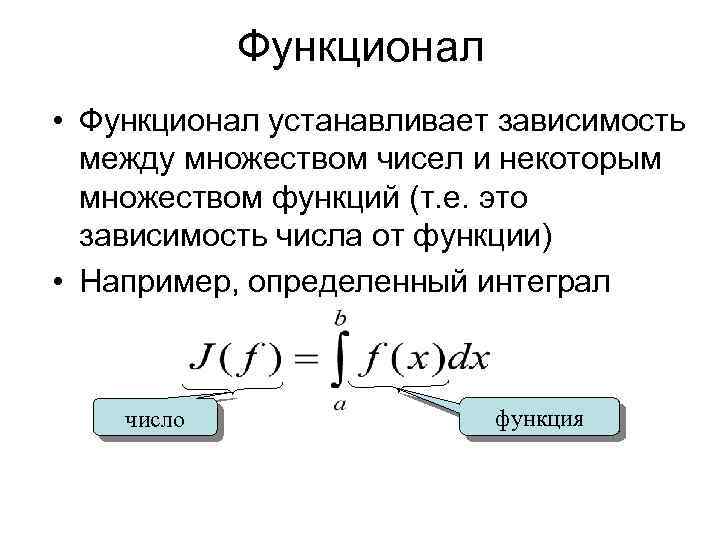Функционал • Функционал устанавливает зависимость между множеством чисел и некоторым множеством функций (т. е. это зависимость числа от функции) • Например, определенный интеграл число функция

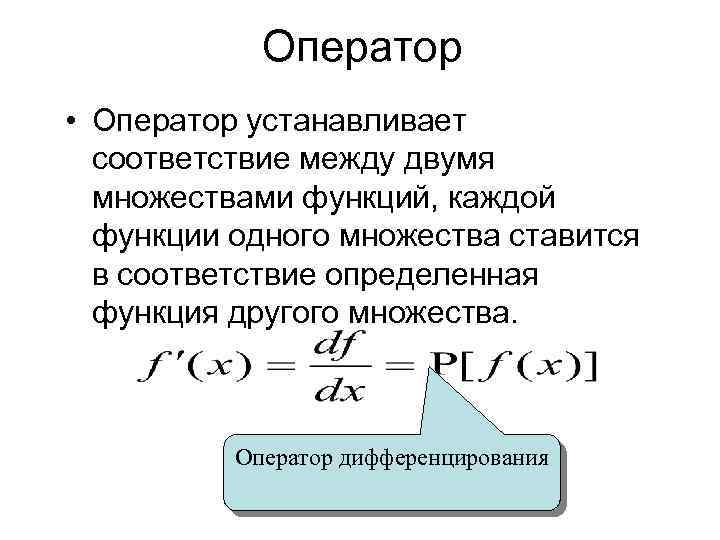Оператор • Оператор устанавливает соответствие между двумя множествами функций, каждой функции одного множества ставится в соответствие определенная функция другого множества. Оператор дифференцирования

Отношения • Термин «отношение» обозначает некоторые виды соответствий, заданные на одном множестве. • Если задано соответствие (Х, R), то о элементе у R(х) говорят, что он находится в отношении R к элементу х: у R х. • Отношением называется пара множеств (Х, R), где R Хn. • Элементами множества Хn являются упорядоченные n-ки, и такое отношение называют n-арным или nместным; множество упорядоченных пар элементов называют бинарным, упорядоченных троек тернарным.

Отношения Если R A 2 - отношение, заданное на множестве А, то • Обратное отношение R-1={(a, b) | (b, a) R} • Дополнение отношения R ={(a, b) | (a, b) R} • Тождественное отношение I = {(a, a) | a A} • Универсальное отношение U= {(a, b) | a A & b A} [U = A 2] • Ядро отношения O = R° R-1

Свойства отношений • Рефлексивность х. Rхистинно ; • Антирефлексивность х. Rх ложно; • Симметричность х. Rу у. Rх; • Антисимметричность (х R у)&(у R х) x=y ; • Несимметричность (полнота, или линейность) Если (х R у) – истинно, то (у R х) – ложно; • Транзитивность (х R у)&(у R z) x R z.

Теорема о свойствах отношений • Если R A A - отношение на множестве А, то тогда – R - рефлексивно – R - антирефлексивно – R - симметрично – R - антисимметрично I R; R I = ; R = R-1; R R-1 I; – R - несимметрично = U; (полно) R I R-1 – R - транзитивно R ° R R;

Отношение эквивалентности • Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. • Элементы множества рассматриваются как эквивалентные тогда, когда любой из этих элементов при некотором рассмотрении может быть заменен другим. • Например, на множестве студентов – отношение «быть в одной группе» или «быть на одном курсе» ; на множестве целых чисел – «иметь одинаковый остаток при делении на число n» .

Классы эквивалентности • Если на множестве Х определено отношение эквивалентности, то подмножество элементов, эквивалентных некоторому элементу х Х, называют классом эквивалентности. • {Aj X | j = 1 n} – множество классов эквивалентности для множества Х. Так как все элементы одного класса эквивалентности эквивалентны между собой, то всякий элемент х Х может находиться только в одном классе. Х будет являться объединением непересекающихся множеств Аj, так что полная система классов {Aj X | j = 1 n} – есть разбиение множества Х. • Каждому отношению эквивалентности на множестве Х соответствует некоторое разбиение множества Х на классы эквивалентности Aj.

Отношения порядка • Отношения порядка определяют порядок расположения элементов множества. • Отношение является отношением нестрого порядка, если оно рефлексивно, антисимметрично и транзитивно ( , , , ). • Отношение является отношением строго порядка, если оно антирефлексивно, несимметрично и транзитивно (<, , >, , ). • Множество Х называется упорядоченным, если сравнимы между собой любые 2 его элемента, то есть для них имеет место x < y или x = y или x > y

Отношение доминирования • Между элементами множества Х имеет место отношение доминирования, если эти элементы обладают следующими свойствами: – Антирефлексивность (никакой элемент не может доминировать над самим собой). – Несимметричность (в каждой паре элементов только один из них может доминировать над другим).

Реализация множеств • Посредством двоичного вектора • Массив • Связанный список

Двоичный вектор Недостатки: ограниченность количества элементов множества, необходимость упорядочивания элементов множества

Массив • Количество элементов множества ограничено размером массива • Время поиска элемента определяется размером массива (справедливо для неупорядоченных массивов) • Для хранения массива необходимо выделять память (частично справедливо для динамических массивов) • Более сложная реализация операций над множествами

Связанный список • Количество элементов списка ограничено размером оперативной памяти • Время поиска определяется длиной списка

Применение множеств • • Словарь Хэш – таблицы Очередь с приоритетами Отношение «многие – ко – многим» и мультисписки • Деревья двоичного поиска

Словарь • Часто возникает задача проверить наличие в множестве некоторого элемента. Для таких целей используется словарь, который может быть как упорядоченным, так и неупорядоченным. • Недостаток: быстрый рост времени выполнения поиска по мере роста словаря

Хэш - таблица • Множество разбивается на подмножества, называемые сегментами. Задаётся хэш – функция, принимающая уникальное значение для каждого сегмента. • Открытое хеширование – в таблице сегментов хранятся значение хэш – функции и указатель на список элементов сегмента • Закрытое хеширование – элементы сегмента хранятся в таблице сегментов

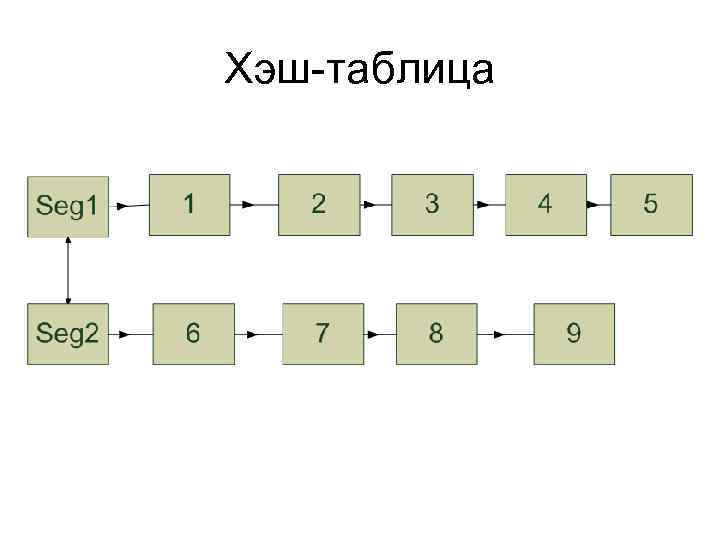Хэш-таблица

Очереди с приоритетом • На множестве элементов задана функция приоритета, принимающая целочисленные значения или значения из линейно упорядоченного множества • Пример: планирование разделения времени процессора, приоритеты при передаче данных • Реализация – связанный список, частично упорядоченное дерево

Отношение «многие – ко – многим» и мультисписки • Мультисписок – структура, в которой каждый элемент имеет более одного указателя и может принадлежать одновременно нескольким спискам • Пример – список учебных курсов и посещающих их студентов

Деревья двоичного поиска • Дерево, узлы которого хранят элементы множества. • Все элементы, хранящиеся в узлах левого поддерева любого элемента x всегда меньше x, а узлы правого поддерева – всегда больше x. • Если обойти дерево во внутреннем (симметричном) порядке, то полученный список будет отсортирован в соответствии с заданным отношением порядка

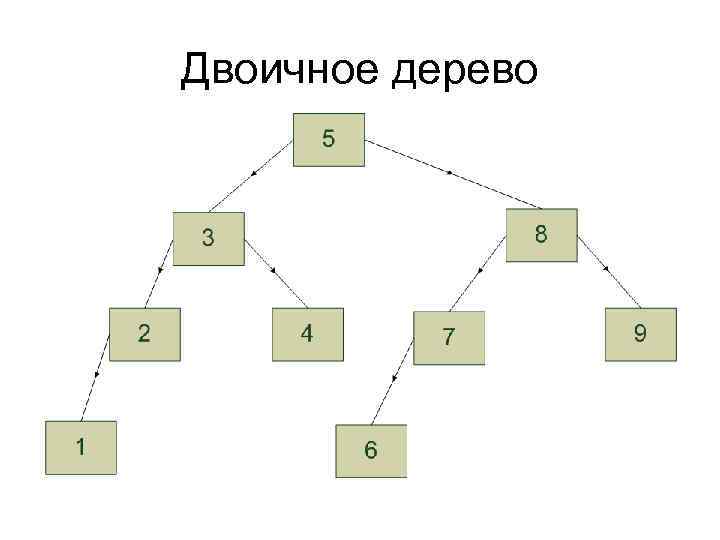Двоичное дерево