Дискретна математика Професор Погорілий Сергій Дем’янович 2 Мета

Дискретна математика Професор Погорілий Сергій Дем’янович

2 Мета і предмет навчальної дисципліни Інформація про курс Мета навчальної дисципліни "Дискретна математика" полягає в оволодінні студентами 1-го курсу напряму підготовки „Комп’ютерна інженерія” математичними засадами новітніх комп’ютерних та інформаційних технологій і формуванні навичок розв’язання базових задач, а також світогляду студентів у галузі застосування методів дискретної математики для ефективного засвоєння комп’ютерних курсів у подальшому навчанні. Предмет навчальної дисципліни "Дискретна математика" включає основні відомості з теорії фінітних та нескінченних множин, методів булевої алгебри, алгоритмів аналізу таких дискретних структур як графи та методів синтезу скінченних автоматів.

3 Структура курсу. Розподіл годин Інформація про курс Модуль 1. Вступ до теорії множин. Булева алгебра. – 14 годин. Закінчується контрольною роботою (останній тиждень березня); Модуль 2. Вступ до теорії графів. Синтез скінченних автоматів. – 20 годин. Закінчується колоквіумом (перший тиждень травня); Практична робота. Самостійна робота студента, розвязання задач з курсу дискретної математики на семінарських заняттях та у вигляді домашніх завдань. Іспит.

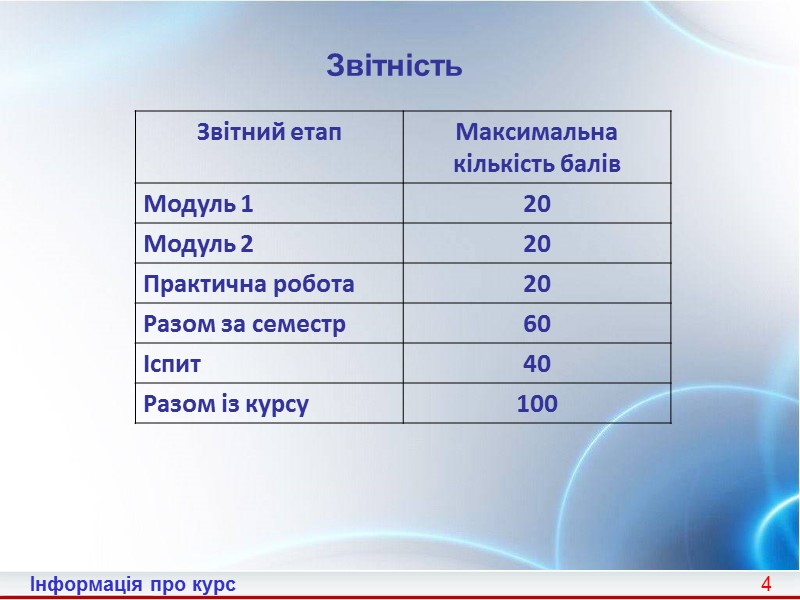
4 Звітність Інформація про курс

5 Література Інформація про курс Погорілий С.Д. Програмне конструювання. ВПЦ Київський університет. 2-е видання, 2007, 438 с. 2. Погорілий С.Д., Калита Д.М. Комп'ютерні мережі. ВПЦ Київський університет. 2007, 456 с. 3. Згуровський М.З., Панкратова Н.Д. Основи системного аналізу. Серія «Інформатика» за редакцією академіка НАНУ Згуровського М.З. Київ, видавнича група BHV, 2007. – 544 с. Література

6 Інформація про курс Література [4, 5, 7 – 14, 18 – 22, 25, 27 – 29]

7 Модуль 1. Вступ до теорії множин. Булева алгебра Вступ до теорії множин

8 Вступ до теорії множин. Відношення Лекція 1 Вступ до теорії множин

Вступ до теорії множин 9 Поняття множини Засновник теорії множин німецький математик Г.Кантор розумів множину як об'єднання до єдиного цілого об'єктів, які ми розрізнюємо інтуїтивно або подумки. Терміни множина, сукупність, колекція, зібрання, масив, об'єднання цілком рівноправні. Далі як основний використовуватимемо лише термін множина. Дискретна математика оперує переважно фінітними (скінченними) множинами. Вступ до теорії множин Вступ до теорії множин Вступ до теорії множин

Вступ до теорії множин 10 Георг Кантор (3.03.1845 - 6.01.1918) Німецький математик, народився у Санкт-Петербурзі. Відомий як творець теорії множин, що стала наріжним каменем в математиці. Кантор дав визначення нескінченних і цілком-упорядкованих множин і довів, що дійсних чисел «більше», ніж натуральних. Визначив поняття кардинальних і порядкових чисел та їх арифметику. Теорія Кантора про трансфінітні числа спочатку була сприйнята настільки нелогічною, парадоксальною і навіть шокуючою, що натрапила на різку критику з боку математиків-сучасників, а згодом стала класичною математичною дисципліною.

Вступ до теорії множин 11 Надалі позначатимемо множини великими літерами, а при переліченні елементів множин братимемо їх у фігурні дужки, наприклад, B = {b1, b2, ..., bn}. Після вертикальної риски у фігурних дужках може бути записано закон, якому підпорядковано елементи множини, що розглядається, наприклад A = {2aa = 1, 2, ...} (множина всіх парних натуральних чисел). Кількість елементів у множині позначатимемо  (іноді це записують як Card()). Якщо множина не містить елементів, вона позначається як . Позначення множин

Вступ до теорії множин 12 Підмножини та надмножини Якщо множина A входить до множини B, то кажуть, що A є підмножиною B, а B – надмножиною A та позначають їх як AB або AB. Множини A та B називають еквівалентними, якщо AB і BA. Нехай існує деяка множина A. Множини A та  називаються невласними підмножинами множини A, а всі інші підмножини A – її власними підмножинами. Операції над множинами можуть бути теоретико-множинними, алгебраїчними або мішаними.

Вступ до теорії множин 13 Об'єднанням множин A та B називатимемо множину AB, елементи якої належать множині A чи B, AB  a(aA)(aB). Для n множин Ai записують Теоретико-множинні операції. Об'єднання множин

Вступ до теорії множин 14 Переріз множин Перерізом множин A та B називатимемо множину AB, елементи якої належать як множині A, так і множині B, AB  a(aA)(aB). Для n множин Ai записують .

Вступ до теорії множин 15 Різниця множин Різницею множин A та B назвемо множину A\B, що складається з тих і тільки тих елементів, які належать A та не належать B, A\B = {a(aA)(aB)}.

Вступ до теорії множин 16 Доповнення множини , де BV. Припустимо, що A та B – підмножини деякої множини V. Доповненням множини A до множини V називають і через = V\A. Важливо підкреслити, що операцію різниці може бути застосовано до довільних множин A та B, у той час як операцію визначення доповнення множини A до множини V – лише за умови, що AV. Має місце рівність A\B = A , де BV.

Вступ до теорії множин 17 Диз’юнктивна сума множин Диз'юнктивною сумою множин A та B називають і через AB позначають множину, елементи якої належать тільки множині A або тільки множині B (виключне OR), AB = {a(aAB)((aAB)(aA\B)(aB\A))}. Для n множин Ai

Вступ до теорії множин 18 Алгебраїчна операція над множинами. Декартів добуток множин Нехай A та B – дві довільні множини елементів. Множина C = A  B називається декартовим або прямим добутком множин A та B, якщо для будь-якого cC має місце співвідношення c = (a, b), де aA та bB, AB = {(a, b)(aA)(bB)}. Інакше кажучи, довільний елемент c є парою, на першому місці якої стоїть довільний елемент a, на другому – довільний елемент b. Дві пари (a, b) та (a', b') вважаються рівними тоді й тільки тоді, коли a = a' та b = b'. Приклад. Якщо A = {a1, a2}, а B = {b1, b2, b3}, то декартовим добутком множин A та B є множина C = {(a1, b1), (a1, b2), (a1, b3), (a2, b1), (a2, b2), (a2, b3)}.

Вступ до теорії множин 19 Декартів добуток множин Для довільного елемента cC співвідношення a є першим елементом пари c і b є другим елементом пари c функціональні за a та b, відповідно. Вони визначають відображення AB на A та AB на B, що позначаються через pr1, pr2 і називаються першою та другою проекціями. Замість a є першим елементом пари c кажуть a – перша проекція c і пишуть a = pr1(c) або pr1(c)A. Співвідношення a = pr1(c) і b = pr2(c) є еквівалентним співвідношенню c = (a, b).

Вступ до теорії множин 20 Мішані операції. Cума множин Сумою множин A та B називають і через A+B позначають об'єднання множин A' та B' таких, для яких існують взаємно однозначні відображення, відповідно A на A' та B на B'. Інакше кажучи, сума множин A та B являє собою об'єднання перенумерованих множин A' та B'. Множини A' та B' утворюються у такий спосіб. Введемо у розгляд множину індексів I = {1, 2, ...}, яка містить кількість елементів, що дорівнює кількості множин, які підсумовуються. Вважатимемо, що A' = {1}A та B' = {2}B. Зрозуміло, що відображення a(1, a) та b(2, b) – суто взаємно однозначні відображення A на A' та B на B'. Тому A + B = ({1}A)({2}B).

Вступ до теорії множин 21 Cума множин Кажуть, що сума множин A та B утворюється приєднанням множини B до множини A. Якщо AB = , то у такому й тільки у такому частинному випадку об'єднання множин A та B збігається з їх сумою, тобто A + B = AB. Якщо заздалегідь нічого не відомо про множини A та B, то у загальному випадку сума цих множин утворюється у вказаний вище спосіб. Для n множин Ai Cума множин

Вступ до теорії множин 22 Відношення Нехай A1, A2, ..., An – довільні множини (не обов'язково відмінні). Під n-арним відношенням, або n-відношенням n на множинах A1, A2, ..., An розуміємо закон (характеристичну властивість), що виділяє у декартовому добутку A1A2 ... An деяку підмножину nA1A2...An та називається графіком відношення n. Якщо A1 = A2 = ... = An = A, то кажуть про n-відношення n на множині A із графіком n An. Досить часто поняття n-відношення ототожнюють із графіком, тобто під n-відношенням на A1, A2, ..., An розуміють саме підмножину nA1A2 ... An.

Вступ до теорії множин 23 Відношення (2) Якщо (ai(1),ai(2),…,ai(n))n, то кажуть, що елементи ai(1),ai(2),…,ai(n) знаходяться у відношенні n, n:n(ai(1),ai(2),…,ai(n)), отже позначення (ai(1),ai(2),…,ai(n))n і n(ai(1),ai(2),…,ai(n)) є еквівалентними. Послідовність (ai(1),ai(2),…,ai(n))n називається елементом або вектором n-відношення n. Відношення, графіки яких складаються із фінітної множини векторів, називаються скінченними n-відношеннями. Якщо n = , то n-відношення n називається порожнім (n). Якщо ж n = , то n називається універсальним (n). Відношення (2) Відношення (2) Відношення (2)

Вступ до теорії множин 24 Відношення (3) Підмножинами декартового добутку є n-відношення, тому існують різноманітні способи їх задання, аналогічні способам задання множин. Наприклад, графік n зручно задавати матрицею, рядки якої є векторами відношення n. Якщо j = {(ai(1),ai(2),…,ai(n))j = 1, 2, ..., m} – множина всіх векторів відношення n, то його графік може бути представлено у матричній формі (наступний слайд). Відношення 1 на множині A називаються унарними, 2 на множинах A1 та A2 – бінарними, 3 на множинах A1, A2 та A3 – тернарними.

Вступ до теорії множин 25 Матричне задання n-відношення n = .

Вступ до теорії множин 26 Унарні відношення Унарне відношення 1 на множині A є характеристичною властивістю деякої підмножини 1A. Множина всіх унарних відношень на A збігається із множиною всіх підмножин множини A. Якщо A = {a1, a2, ..., an} (|A| = n), то кількість унарних відношень на A дорівнює 2n. Приклад 1.1. Нехай задано множину N = {1, 2, ..., n}. Тоді відношення, показані нижче, унарні. 1 = {3, 7, 10, 11, ..., 19} 1 = {nза будь-якого n  k} 1 = {nза будь-якого n  m} 1 = {2kk = 1, 2, ...} 1 = {2k-1k = 1, 2, ...}. Парність та непарність є унарними відношеннями на множині N.

Вступ до теорії множин 27 Бінарні відношення (1) Бінарне відношення 2 на множинах A та B визначається графіком 2AB. Якщо елементи aA та bB знаходяться у відношенні 2, то поряд із позначеннями (a, b)2 і 2(a, b) часто пишуть a2b. A називається областю визначення, B – областю значень відношення 2. Відношення {(b, a)|(a, b)} називається оберненим до відношення  і часто позначається через –1. Крім матричного, існують й інші способи задання бінарних відношень за допомогою таблиць і стрілок.

Вступ до теорії множин 28 Приклад 1.2. Є дві множини A = {2, 3, 5} і B = {2, 3, 4, 5, 6}. Графік бінарного відношення 2 на множинах A та B такого, що ai2bj тоді й тільки тоді, коли ai є дільником bj, має вигляд: Бінарні відношення (2) 2 = .

Вступ до теорії множин 29 Представлення бінарного відношення у вигляді таблиці Представлення бінарного відношення у вигляді таблиці Нижче наведено представлення відношення 2 з Прикладу 1.2 у табличному вигляді:

Вступ до теорії множин 30 Представлення бінарного відношення у вигляді стрілок Нижче наведено представлення відношення 2 з Прикладу 1.2 у вигляді стрілок (рис. 1.1 a). У наведеному прикладі множина A входить до множини B, AB, тому дане бінарне відношення може бути представлене так, як показано на рис. 1.1 б. а б

Вступ до теорії множин 31 Бінарні відношення (3) Приклад 1.3. Розглянемо множину N = {1, 2, ...}. Бінарні відношення (<2), (>2), (=2), (2) та (2) визначаються графіками (<2) = (>2) = (2) = (2) = (=2) = , , , ,

Вступ до теорії множин 32 Бінарні відношення (4) Приклад 1.4. Підмножина 2  DD (D – множина дійсних чисел) є графіком деякого бінарного відношення на D. Відношення x = y та x < y показано на рис. 1.2 а та б. а б

Вступ до теорії множин 33 Бінарні відношення (5) Приклад 1.5. Нехай F(A) – множина всіх слів скінченної довжини над алфавітом A = {a1, a2, ..., an}. Відношення < на множині F(A) визначається графіком (

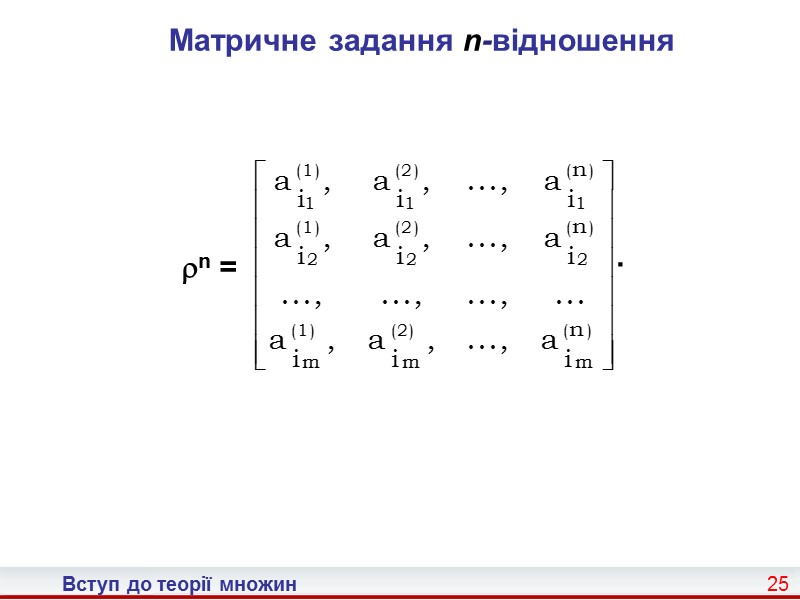
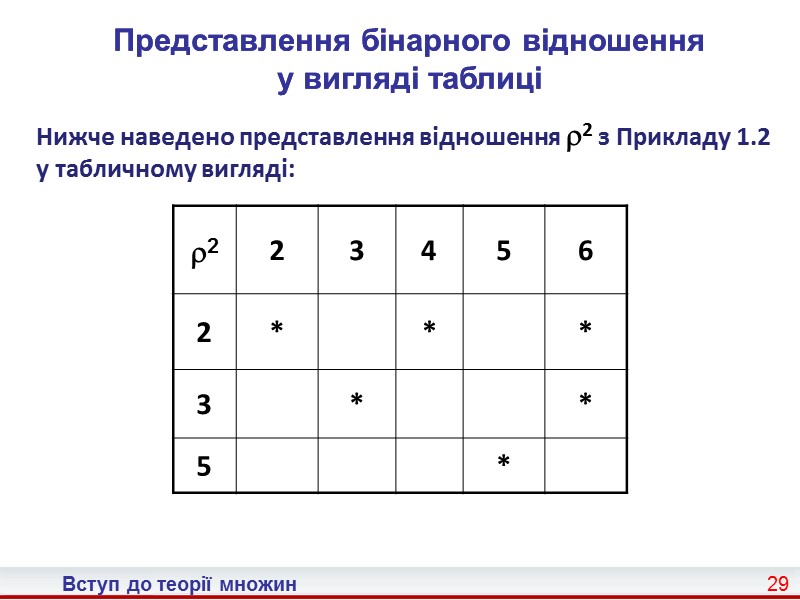
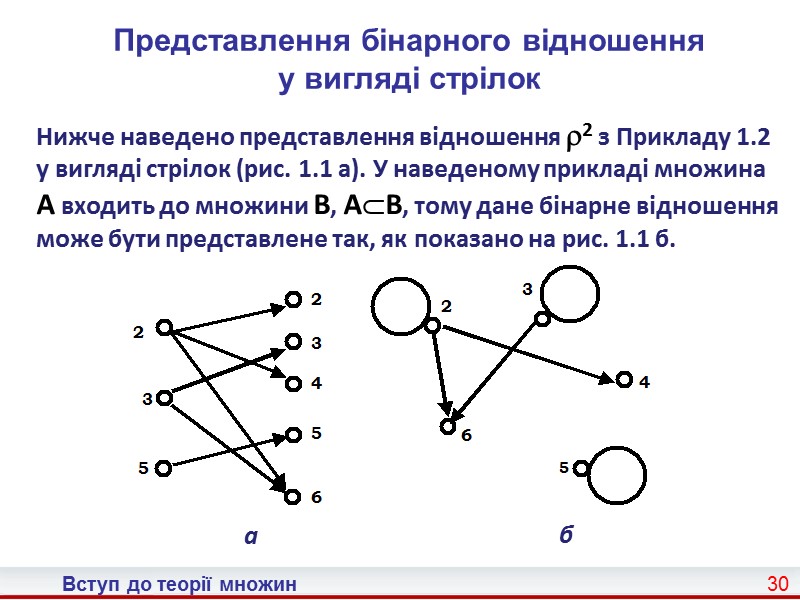
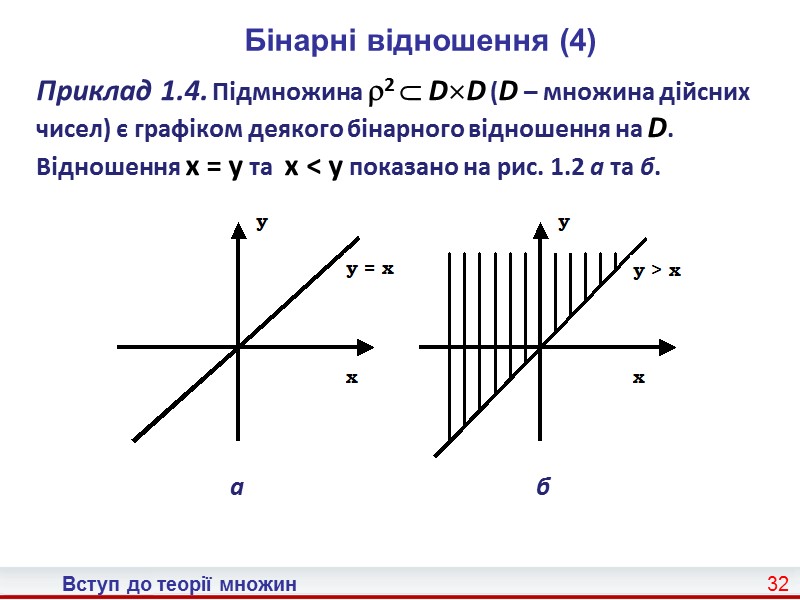
Вступ до теорії множин 34