ДИНАМИКА ТВЕРДОГО ТЕЛА ЛЕКЦИИ 1, 2 :

ДИНАМИКА ТВЕРДОГО ТЕЛА ЛЕКЦИИ 1, 2 : ГЕОМЕТРИЯ МАСС

Рассмотрим прямую (ось) и систему материальных точек с массами , так, что расстояние от от ii — ой точки до оси равно . Величина называется моментом инерции системы относительно оси 1. Определение момента инерцииl 1, nm m. Kir 2 1 n l i i i I m r l Для непрерывно распределенных масс 2 2 l V V I r dm r dv Для однородного ( ) тела Const /M V 2 l V M I r dv V Задача: научиться считать момент инерции любого тела относительно любой оси

2. Физический смысл момента инерцииl Момент инерции представляет собой меру инерции тела во вращательном движении Произведение момента инерции тела на его угловое ускорение равно сумме моментов всех сил, приложенных к телу ll d d I t M m dv dt F сравните вращательное движение поступательное движение 21 2 l. KI 21 2 Kmv

3 a. Моменты инерции простейших 1 — D и 2 -D тел 3 2 22 1 2 2 3 3 a a M M a I x dx Ma a a Стержень. Ось проходит через середину стержня, перпендикулярно ему aa x

3 b. Моменты инерции простейших 1 — D и 2 -D тел Диск. Ось проходит через середину диска, перпендикулярно ему24 2 2 2 0 0 0 2 2 1 4 2 a a M M M a I r rdrd r rdr Ma a a

3 c. Моменты инерции простейших 1 — D и 2 -D тел Прямоугольный треугольник. Ось проходит через катетb a x /y b b a x 3 3 22 1 3 4 6 M ba ba Ma ab ( / ) 2 2 0 0 0 2 2 ( / ) b b a xa a M M I x dydx x b b a x dx ab ab

4 a. Моменты инерции простейших 3 — D тел 2 2 8 a b c x a b c M I y z dxdydz abc Прямоугольный параллелепипед. 2 a 2 b 2 c x y z 3 3 2 22 2 2 8 3 3 3 M c b M a b c abc

4 b. Моменты инерции простейших 3 — D тел Шар. Ось проходит через центр 2 2 2 33 (4 / 3)V M I x y z y x z dv a 2 2 3 3 0 2 2 6 4 (4 / 3) 5 a V M M r dv r r dr Ma a a x y z Из соображений симметрии x y z. I I 22 5 I Ma a

5. Радиус инерции 2 0 I Mr Момент инерции относительно оси можно выразить в виде Стержень 0 3 a r Диск 0 2 a r Треугольник 0 6 a r Параллелепипед 2 2 0 3 b c r Шар0 2 5 r a Величина называется радиусом инерции тела относительно данной оси 0 r По определению радиус инерции есть длина, равная расстоянию от данной оси той точки, в которой нужно сосредоточить массу всей системы, чтобы получить тот же момент инерции.

Момент инерции II относительно оси равен сумме момента инерции II CC тела относительно параллельной оси, проходящей через масс и произведения массы тела на квадрат расстояния между осями 6. Теорема (Гюйгенса-Штейнера) о параллельных осях. C x y zd r 1 r 2 CI r dm 2 1 I r dm 2 2 2 12 cos 2 r r d rd r d dy 2 22 I r dm d ydm CI 2 Md 0 CMy 2 CI I d M Очевидное обобщение 2 2 1 2 I I d d M 2 1 1 CI I d M 2 2 2 CI I d M

Момент инерции плоской фигуры относительно оси zz , перпендикулярной плоскости фигуры, равен сумме моментов инерции фигуры относительно двух других осей, лежащих в ее плоскости 7. Теорема о перпендикулярных осях2 z. I r dm 2 x. I y dm 2 2 2 r x y z x y. I I I x y z r 2 y. I x dm dm

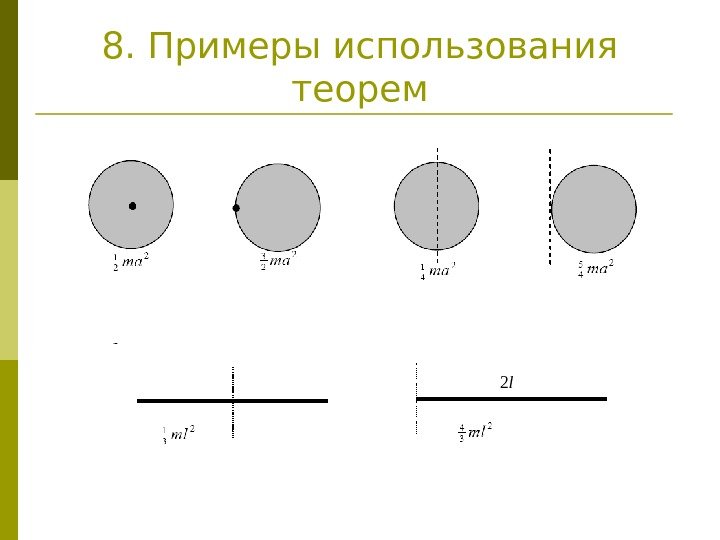
8. Примеры использования теорем 2 l

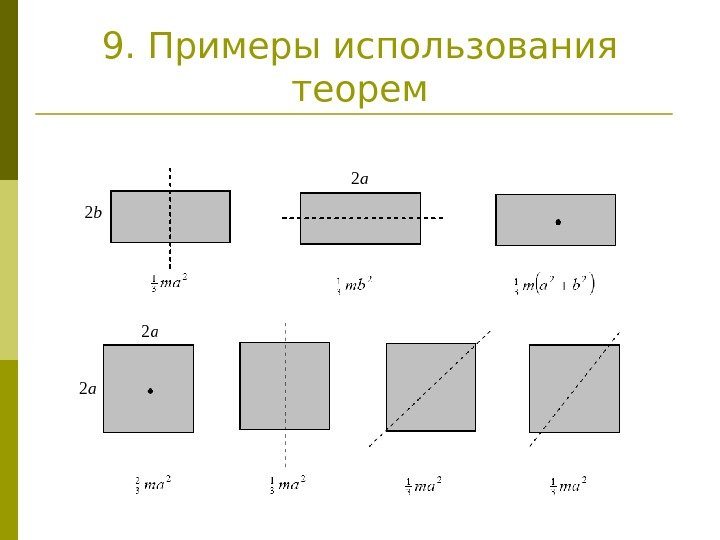
9. Примеры использования теорем 2 a 2 b 2 a 2 a

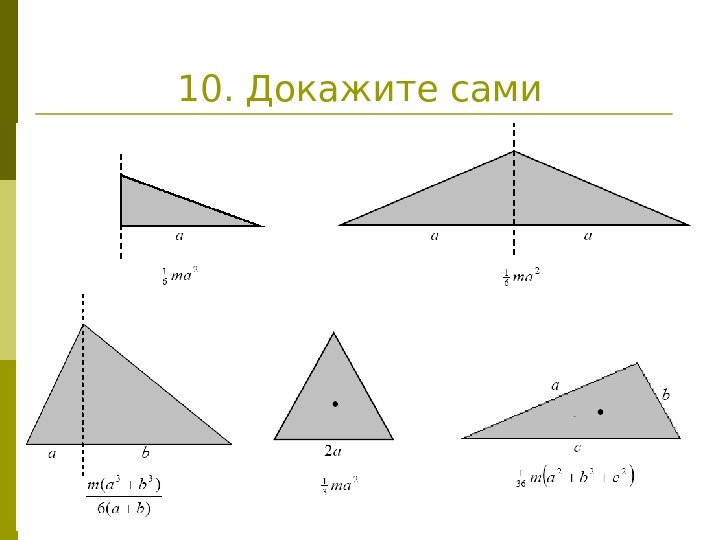
10. Докажите сами

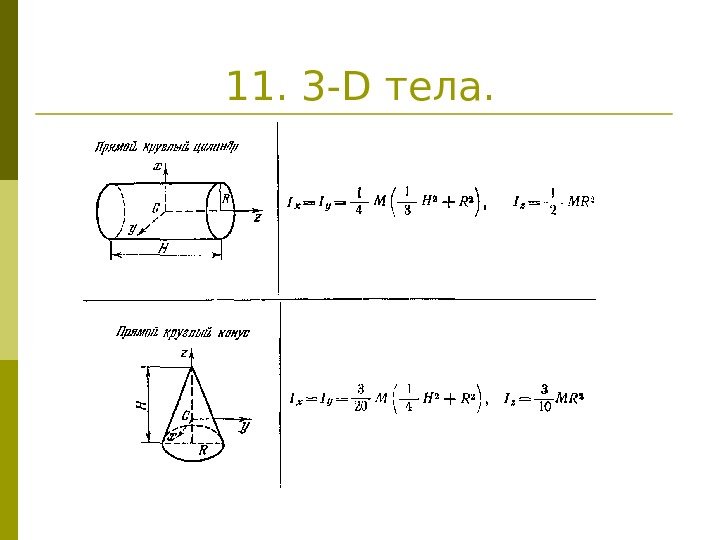
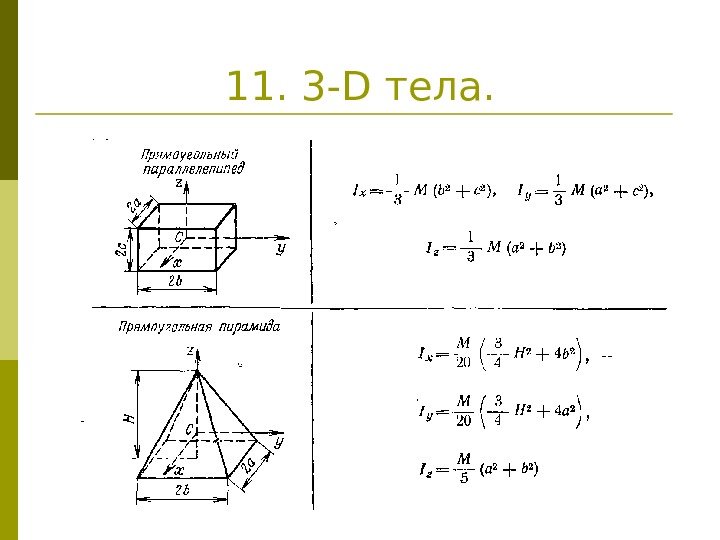
11. 3 — D тела.

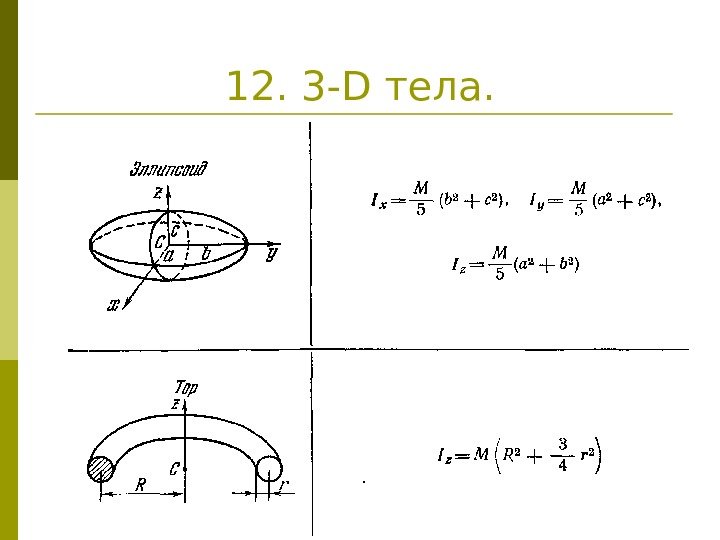
11. 3 — D тела.

12. 3 — D тела.

13. Моменты инерции относительно осей, выходящих из данной точкиx Oy zl 0 l. N P 0 cos cos l i j k , , x y zcos cos. PN x y z 0 i j k l × ON uuur cos cos cosz y x i j k 22 2 2 2 2 cos cos. PN y z z x x y 2 cos cos 2 cosxy yz zx 2 2 2 2 2 cos cosl V V V I y z dm z x dm x y dm 2 cos cos 2 cos V V V xydm yzdm zxdm , , x y z. I I I, , xy yz zx. I I I моменты инерции относительно осей центробежные моменты инерции 2 2 2 cos cos 2 cosl x y z xy yz zx. I I I I

14. Тензор инерции, , xy yz zx. I I I x xy xz yx y yz zx zy z I I I I I I Тензор инерции , 1 : 0 T x x x I x Некоторые свойства тензора инерции 1) Симметричность ij ji. I I 2) Положительная определенность 3 0 0 0, 0, , 1 T l ij i j I I l l l I l , , x y z. I I I, z x y. I I I 3) Неравенства для 2 2 2 x y y z x z Геометрическое толкование: из трех отрезков, длины которых пропорциональны моментам инерции относительно трех перпендикулярных осей, всегда можно построить треугольник 4) Неравенства для / 2, / 2 xy z yz x zx y. I I I 2 22 xy x y

15. Эллипсоид инерции Тензору соответствует квадратичная форма. I 2 2 2( , , ) 2 2 2 x y z xy yz zx. F x y z I x I y I z I xy I yz I zx и поверхность уровня ( , , ) 1 F x y z В силу положительной определенности поверхностью уровня является эллипсоид Его называют эллипсоидом инерции. . I Физический смысл эллипсоида инерции Проведем через начало координат в направлении оси прямую до пересечения с эллипсоидом инерции. Обозначим через длину соответствующего отрезка, а через координаты точки пересечения. l R * * * , , x y z * * *cos , cosx R y R z R 1 l R I 2 * * *1 , , l. F x y z R I Длина радиуса-вектора эллипсоида инерции обратно пропорциональна корню квадратному из момента инерции относительно оси, направленной по этому радиусу

16. Главные оси тензора инерции Уравнение эллипсоида можно упростить, если перейти к новым координатным осям , направив их по главным диаметрам поверхности. 2 2 21 x y z a b c ( , , )x y z 0 0 0 x y z I I I I Уравнение эллипсоида инерции в новых осях Тензор инерции в новых осях 1 x a I 1 y b I 1 z c I Как найти главные оси? det 0 I E 1) Найти решения характеристического уравнения. E — единичная матрица 2) Найти собственные вектора как нетривиальное решение уравнения (1) ( 2) ( 3), , ξ ξ ξ ( ) ( ), 1, 2, 3 i i ii Iξ ξ (1) ( 2 ) ( 3), , При этом собственные числа совпадают с , а собственные вектора определят направление главных осей (1) ( 2 ) (3), , x x x. I I I ( , , )x y z (1) ( 2 ) (3), , ξ ξ ξ (1) ( 2 ) (3) (1) ( 2 ) ( 3) трехосный эллипсоид вращения шаровой эллипсоид

Определение предполагает, что 1)1) Выбрана декартова система координат с началом в данной точке 2)2) Одна из осей (скажем ) совпадает с данной осью 3)3) Вычисленные для этой системы координат центробежные моменты 1 7. Главные оси инерции В более широком смысле для данной точки главной осью инерции тела называется ось, для которой оба центробежных момента инерции, содержащие индекс этой оси, равны нулю. , 0 xz yz. I I z Oxyz. O 0 0 x xy yx y z I I I I Свойство быть главной осью не зависит от выбора направлений двух других координатных осей. Возможный вид тензора инерции z 1 z y 1 y x 1 x 0 xz. I xzdm 0 yz. I yzdm 1 cos sinx x y 1 sin cosy x y 1 1 cos sin 0 x z xz yz. I x y zdm I I 1 10 y z. I K

Пусть ось совпадает с одной из главных осей тензора инерции. Выберем две другие оси совпадающими с двумя другими главными осями тензора инерции. В этих осях 18. Главные оси инерции и главные оси тензора инерции 0 xz yz. I I z 0 0 0 x y z I I I I Ось является главной осью инерции тогда и только тогда когда она совпадает с одной из главных осей тензора инерции. , x y 1 11 1, 0 x z y zx y I I Пусть ось является главной осью инерцииz 0 0 x xy yx y z I I I I 0 0 0 x xy yx y z I I I ( 3) z. Idet 0 I E ( 3)Iξ ξ 0 0 0 x z xy x yx y z I I I 0 0 1 x y z

19. Главные центральные оси инерции Главной центральной осью инерции называется главная ось, проходящая через центр масс тела. Свойство быть главной осью зависит не только от самой оси, но и от выбранной точки на ней (начала координат). Вопрос: Когда ось является главной осью для любой лежащей на ней точки? y z 1 z x 1 x 1 y 1 11 1 x z xz CI x z dm x z h dm xzdm h xdm I h. Mx h 1 1 x z CI h. Mx 1 1 y z CI h. My Для того, чтобы ось была главной для точки необходимо и достаточно, чтобы центр масс тела находился на этой оси O 1 O z 1 O Пусть ось главная для точки O 0 xz yz. I I Главная центральная ось инерции является главной осью для всех своих точек, а нецентральная главная ось инерции является главной осью инерции лишь для одной своей точкиz

20. Свойства симметрии 0 xy i i i. I m x y Пусть ось xx есть ось симметрии Если однородное абсолютно твердое тело имеет ось симметрии, то эта ось будет главной осью инерции для всех точек данной оси Тогда каждой частице будет соответствовать такая же частица , , M x y z 0 xz i i i. I m x z EE сли однородное абсолютно твердое тело имеет плоскость симметрии, то для всех точек этой плоскости одна из главных осей инерции будет к ней перпендикулярна ПП римем плоскость симметрии за плоскость ху. В. В сякой частице будет соответствовать такая же частица , , M x y z 0 xz i i i. I m x z 0 yz i i i. I m y z

22. Вычисление моментов инерции относительно произвольных осей. L Пусть для тела известны главные центральные моменты инерции Дана прямая . Как вычислить для нее момент инерции? , , x y z. I I I x y z L ll LP 1) Проводим прямую через центр масс C C d 2) Находим углы между и главными осями инерции l, , 3) Вычисляем момент инерции относительно оси l 2 2 2 cos cosx y z. I I I 0 0 cos cos 0 0 cos x l y z I I 4) По теореме Гюйгенса-Штейнера вычисляем момент инерции относительно оси L 2 L l. I I Md

23. Пример/ 4 OC H / 2 Требуется определить момент инерции прямого кругового конуса относительно образующей SB; радиус основания конуса равен R, высота равна Н. , , x y z главные центральные оси инерции / 2 2 2 sin cosl y z. I I I 2 2 23 3 , 20 4 10 y z H I M R I MR по таблицам 2 2 sin cos R H H R 2 2 2 3 9 20 4 l R I M H R 2 2 3 sin 4 HR d CS H R 2 2 2 3 6 20 L R I M H R

24. Еще пример. KF D E z z. I I · · · 2 2 2 cos , KF KF z x y z. I I x z I y z I z z 2 3 G L g 2 2 sin 3 G L g Вращающаяся часть подъемного крана состоит из стрелы KF длиной L и весом G, противовеса D весом Q и груза Е весом Р. Стрела составляет с вертикальной осью вращения угол . Определить момент инерции крана относительно оси вращения, считая противовес D и груз Е точечными массами, а стрелу — однородной тонкой балкой. Оси х и х’ пп ерпендикулярны к плоскости рисунка. 2 2 2, sin. D E z z Q P I d I L g g / 20 002 2 2 2 sin 3 z Q L G I d P g g