Дифференциальные уравнения Дифференциальным уравнением называется уравнение, связывающее независимую




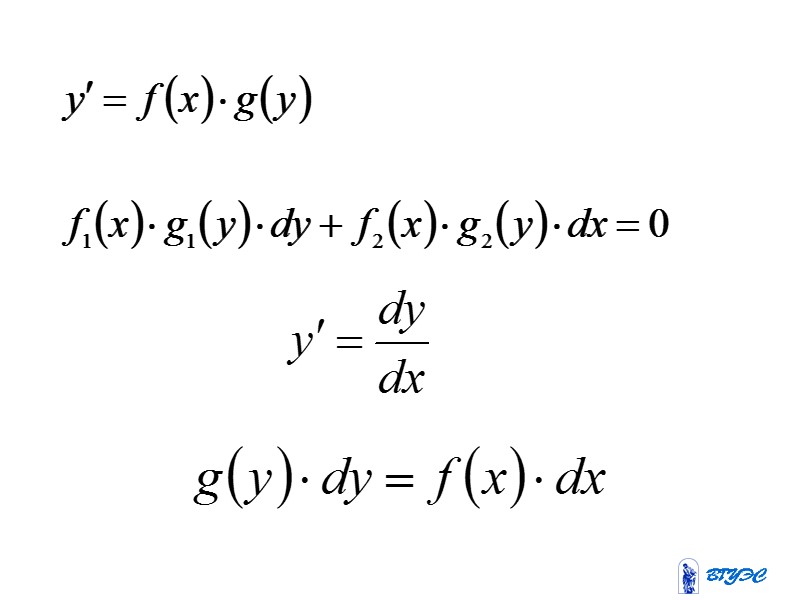

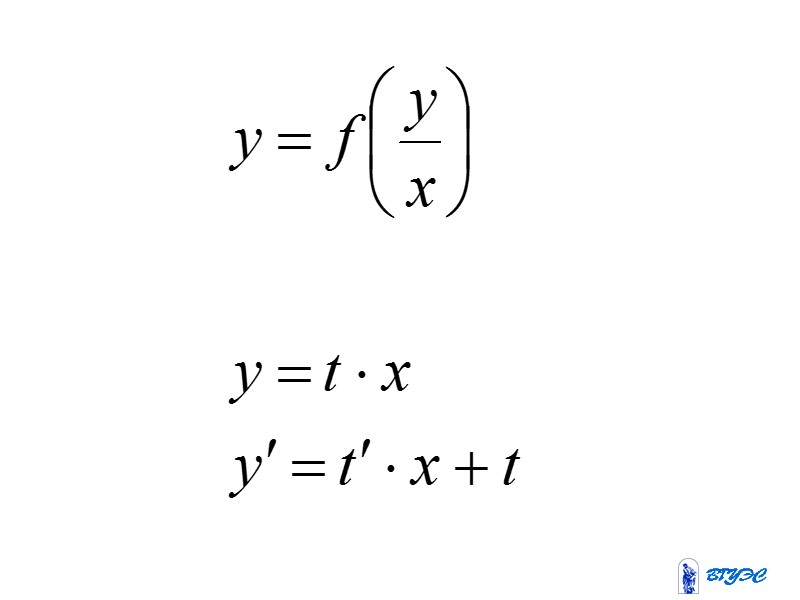

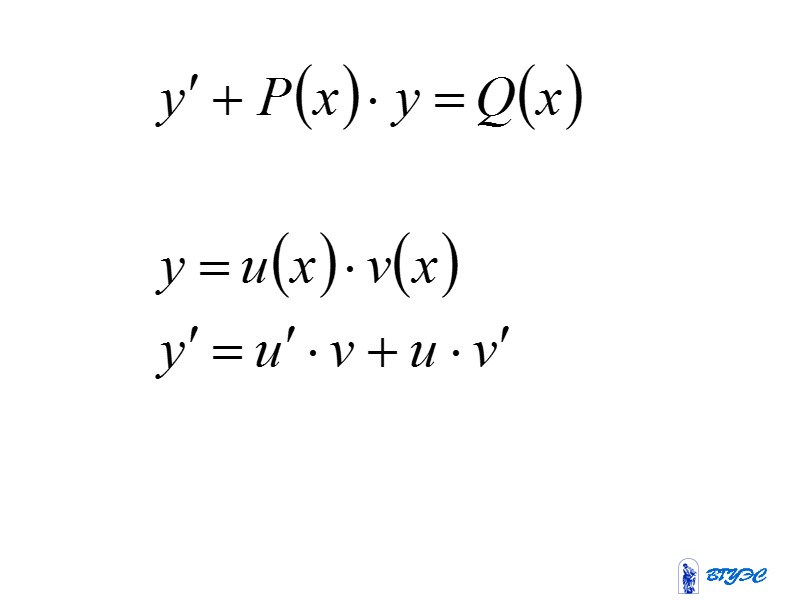
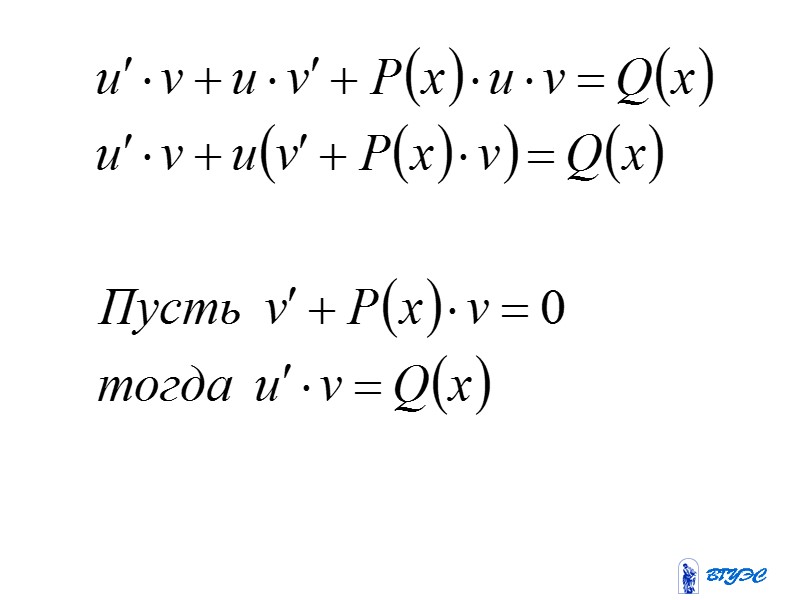







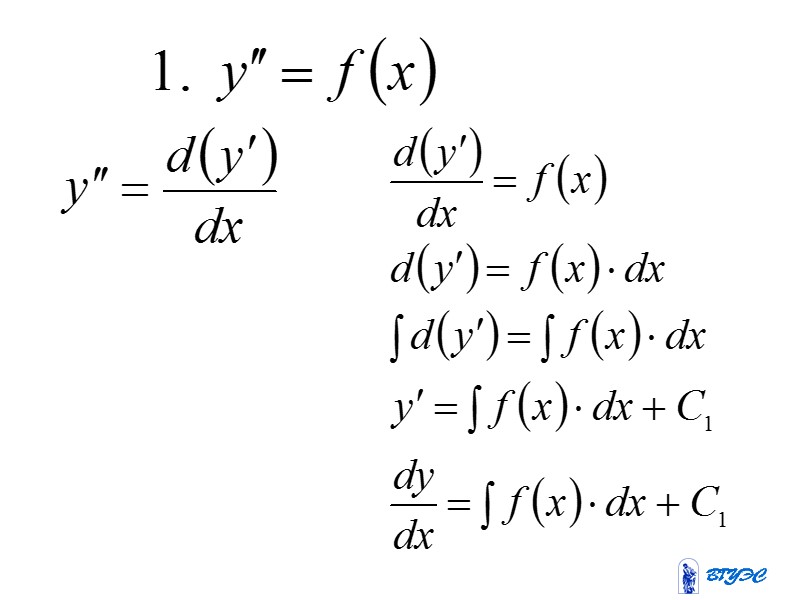
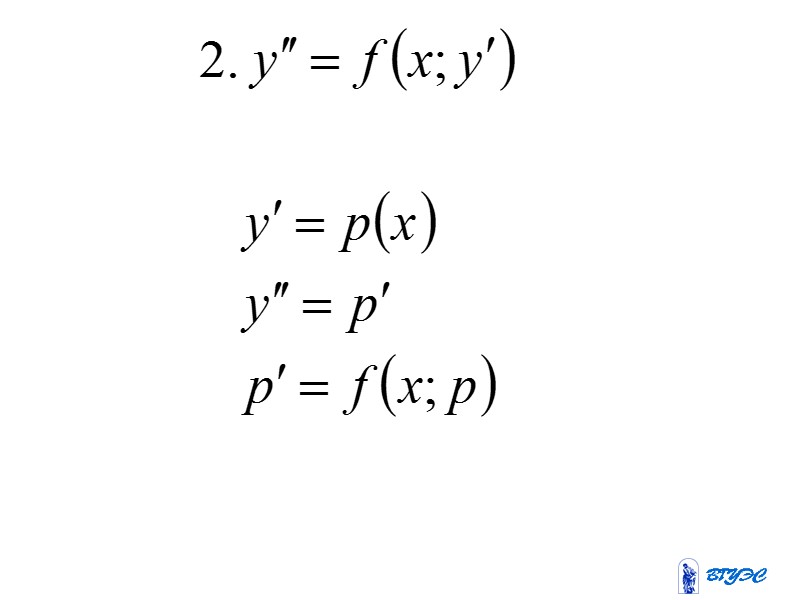





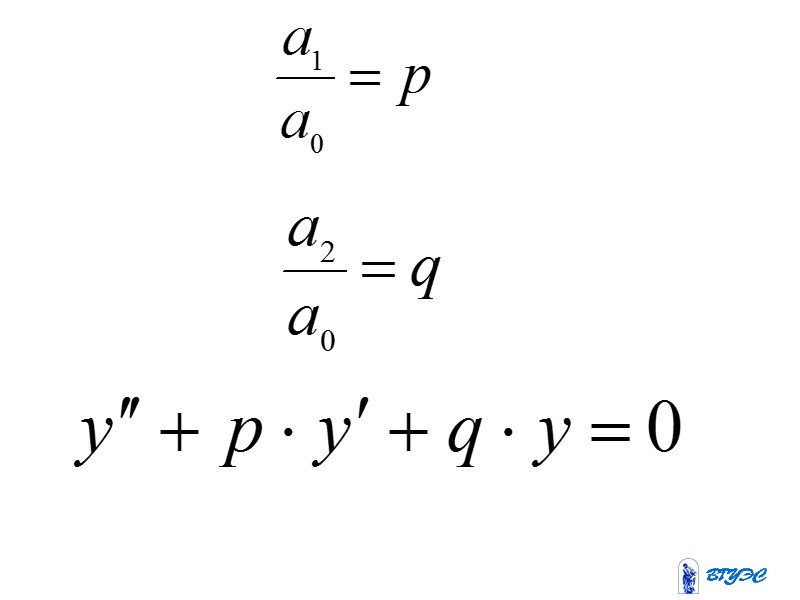


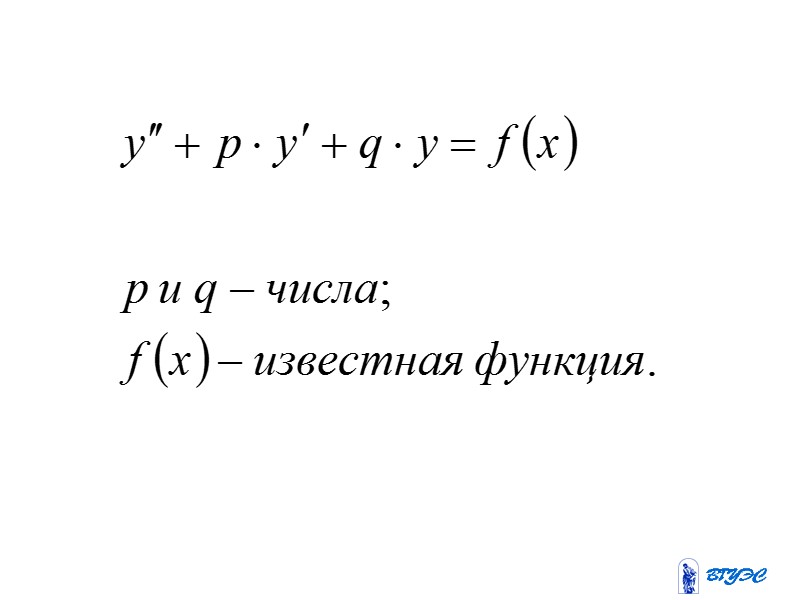









71-6.differencialynye_uravneniya.ppt
- Количество слайдов: 38
 Дифференциальные уравнения
Дифференциальные уравнения
 Дифференциальным уравнением называется уравнение, связывающее независимую переменную , неизвестную функцию и её производные. Наивысший порядок производной, входящей в уравнение называется порядком уравнения.
Дифференциальным уравнением называется уравнение, связывающее независимую переменную , неизвестную функцию и её производные. Наивысший порядок производной, входящей в уравнение называется порядком уравнения.
 Всякая функция , которая, будучи подставленная в уравнение, обращает его в тождество, называется решением этого уравнения. Решить уравнение – значит, найти все его решения в заданной области.
Всякая функция , которая, будучи подставленная в уравнение, обращает его в тождество, называется решением этого уравнения. Решить уравнение – значит, найти все его решения в заданной области.
 Общим решением дифференциального уравнения называется такое его решение , которое содержит столько независимых постоянных, каков порядок этого уравнения. Если общее решение задано в неявном виде то оно называется общим интегралом дифференциального уравнения.
Общим решением дифференциального уравнения называется такое его решение , которое содержит столько независимых постоянных, каков порядок этого уравнения. Если общее решение задано в неявном виде то оно называется общим интегралом дифференциального уравнения.
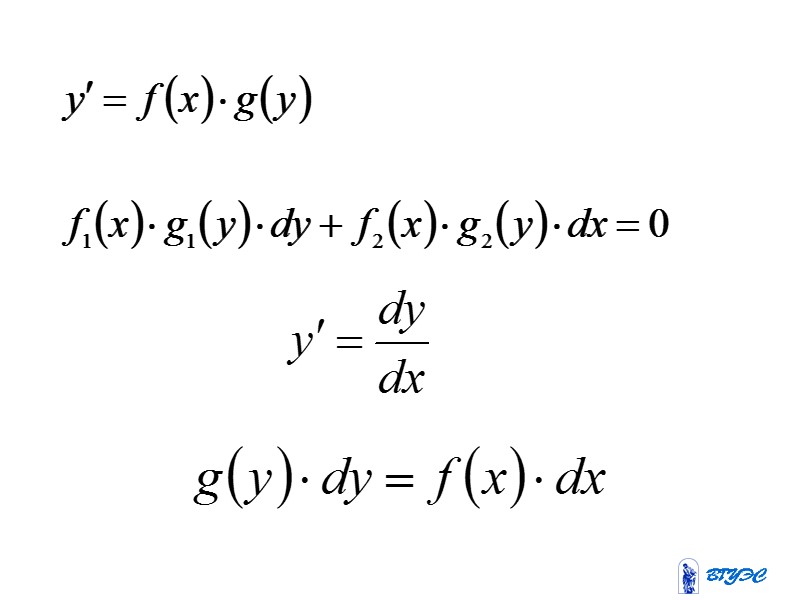 Всякое решение дифференциального уравнения, которое получается из общего решения, если произвольным постоянным, в него входящим придать определенные значения, называется частным решением этого дифференциального уравнения.
Всякое решение дифференциального уравнения, которое получается из общего решения, если произвольным постоянным, в него входящим придать определенные значения, называется частным решением этого дифференциального уравнения.
 Дифференциальные уравнения первого порядка
Дифференциальные уравнения первого порядка
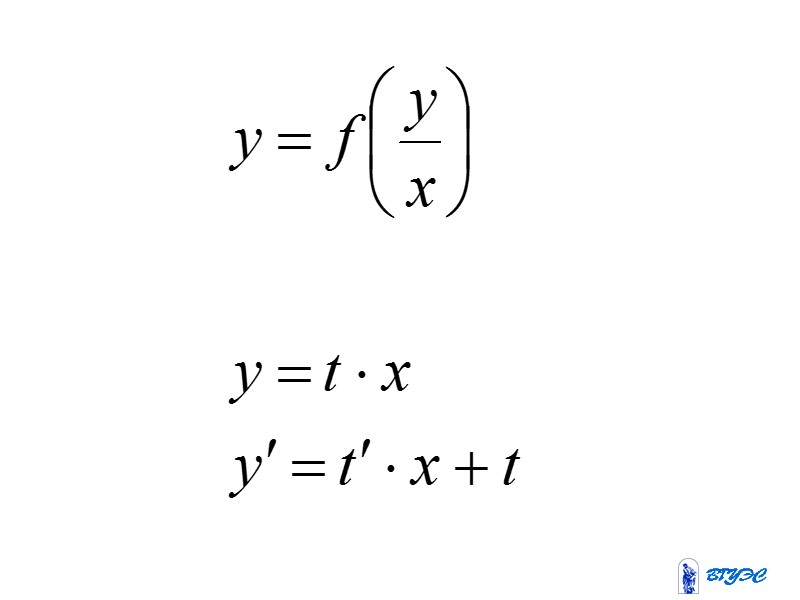 Дифференциальным уравнением первого порядка называется уравнение связывающее независимую переменную , искомую функцию и её первую производную : или .
Дифференциальным уравнением первого порядка называется уравнение связывающее независимую переменную , искомую функцию и её первую производную : или .
 Функция называется общим решением диф.уравнения первого порядка в области , если она удовлетворяют двум условиям: 1) при любых значениях произвольной постоянной , принадлежащих некоторому множеству, функция является решением диф. уравнения;
Функция называется общим решением диф.уравнения первого порядка в области , если она удовлетворяют двум условиям: 1) при любых значениях произвольной постоянной , принадлежащих некоторому множеству, функция является решением диф. уравнения;
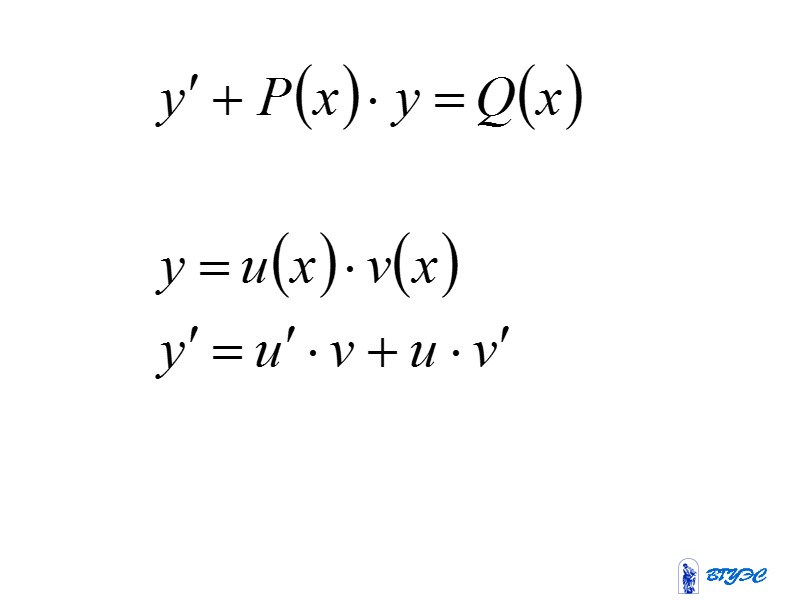 2) какова бы ни была точка , лежащая в обл. , существует единственное значение постоянной , такое, что решение удовлетворяет начальному условию Решение называется частным решением.
2) какова бы ни была точка , лежащая в обл. , существует единственное значение постоянной , такое, что решение удовлетворяет начальному условию Решение называется частным решением.
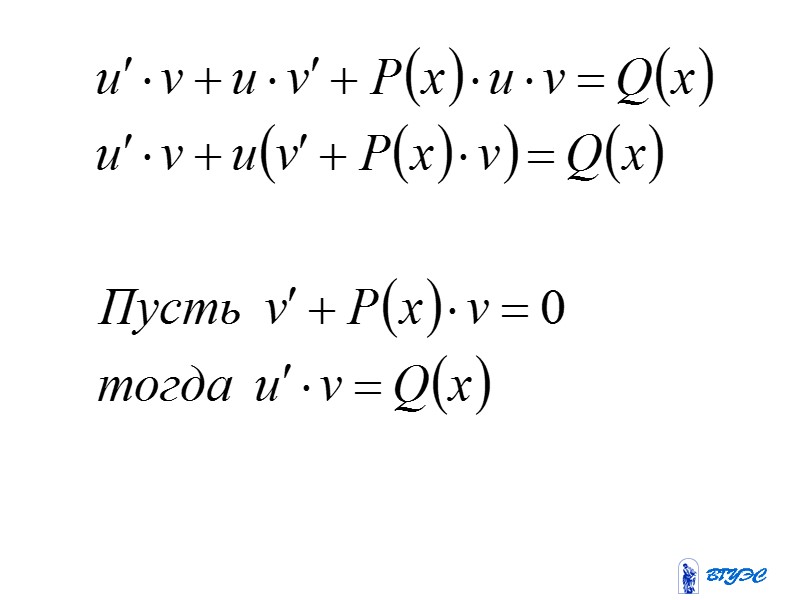 Определение задачи Коши: Задача, в которой требуется найти частное решение уравнения , удовлетворяющее начальному условию , называется задачей Коши. Общее решение , построенное на плоскости , называется интегральной кривой.
Определение задачи Коши: Задача, в которой требуется найти частное решение уравнения , удовлетворяющее начальному условию , называется задачей Коши. Общее решение , построенное на плоскости , называется интегральной кривой.
 Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Не существует общего метода решения дифференциального уравнения первого порядка.
Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Не существует общего метода решения дифференциального уравнения первого порядка.
 Уравнения с разделяющимися переменными
Уравнения с разделяющимися переменными

 Однородные дифференциальные уравнения первого порядка
Однородные дифференциальные уравнения первого порядка

 Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка

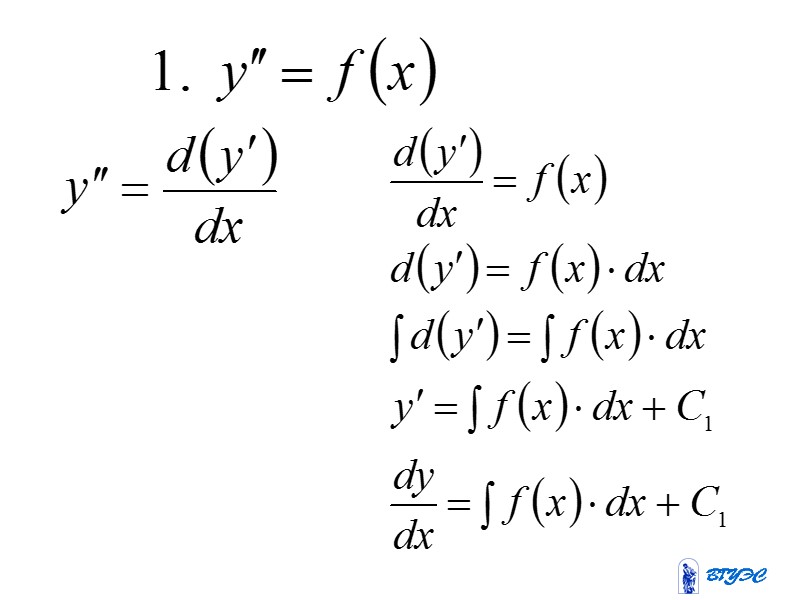
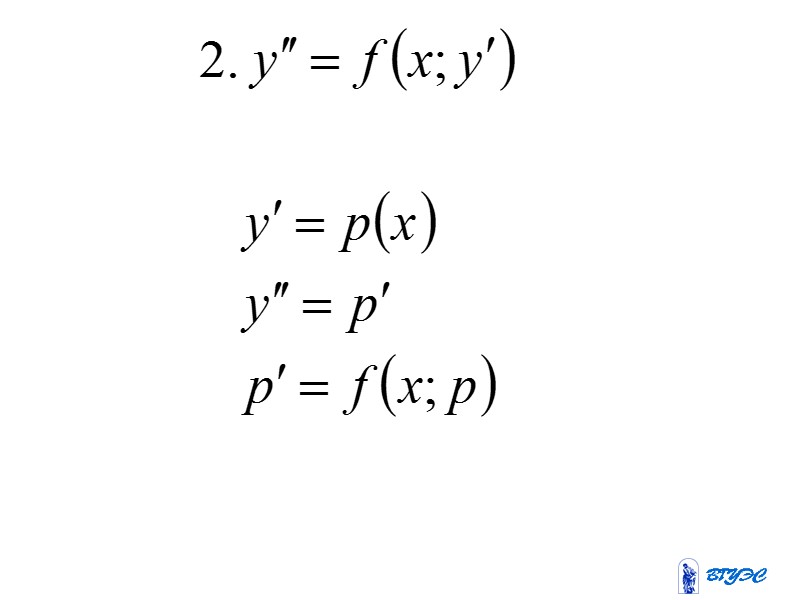 Уравнение Бернулли
Уравнение Бернулли
 Дифференциальные уравнения второго порядка
Дифференциальные уравнения второго порядка
 Дифференциальным уравнением второго порядка называется уравнение связывающее независимую переменную , искомую функцию и её первую и вторую производные :
Дифференциальным уравнением второго порядка называется уравнение связывающее независимую переменную , искомую функцию и её первую и вторую производные :
 Функция называется общим решением диф.уравнения второго порядка в области , если она удовлетворяют двум условиям: 1) при любых значениях произвольных постоянных , принадлежащих некоторому множеству, функция является решением диф. уравнения;
Функция называется общим решением диф.уравнения второго порядка в области , если она удовлетворяют двум условиям: 1) при любых значениях произвольных постоянных , принадлежащих некоторому множеству, функция является решением диф. уравнения;
 2) какова бы ни были начальные условия , , существует единственное значение постоянных такое, что функция является решением уравнения и удовлетворяет начальным условиям
2) какова бы ни были начальные условия , , существует единственное значение постоянных такое, что функция является решением уравнения и удовлетворяет начальным условиям
 Простейшие уравнения второго порядка допускающие понижение порядка
Простейшие уравнения второго порядка допускающие понижение порядка
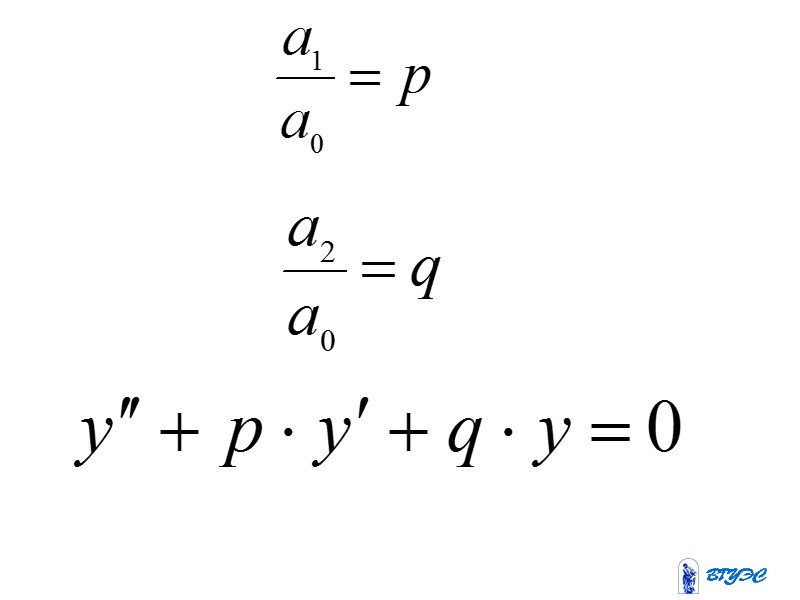


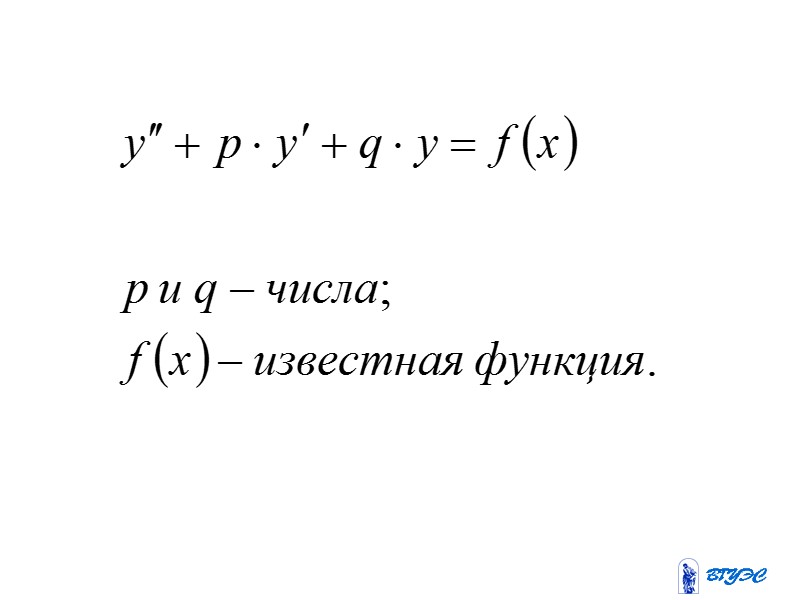 Линейные дифференциальные уравнения второго порядка
Линейные дифференциальные уравнения второго порядка

 Линейные дифференциальные уравнения второго порядка с постоянным коэффициентами
Линейные дифференциальные уравнения второго порядка с постоянным коэффициентами
 1.Линейные однородные диф.уравнения второго порядка с постоянными коэффициентами
1.Линейные однородные диф.уравнения второго порядка с постоянными коэффициентами


 Линейные неоднородные дифференциальные уравнения второго порядка с постоянным коэффициентами
Линейные неоднородные дифференциальные уравнения второго порядка с постоянным коэффициентами



