ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Модуль 5
































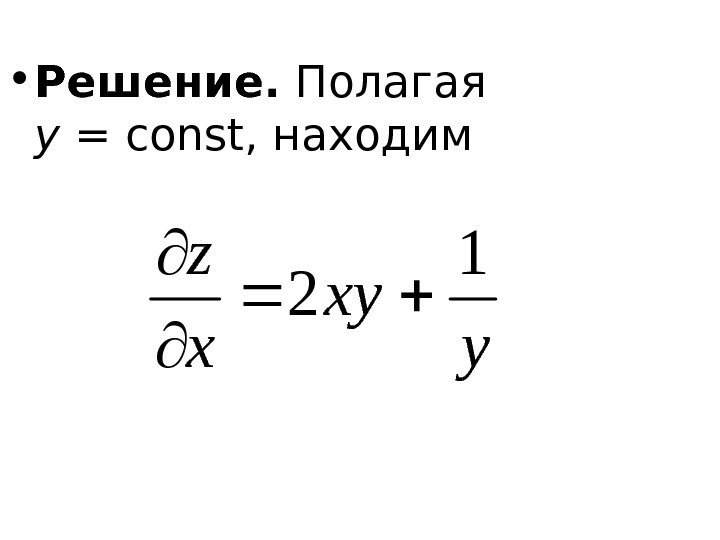


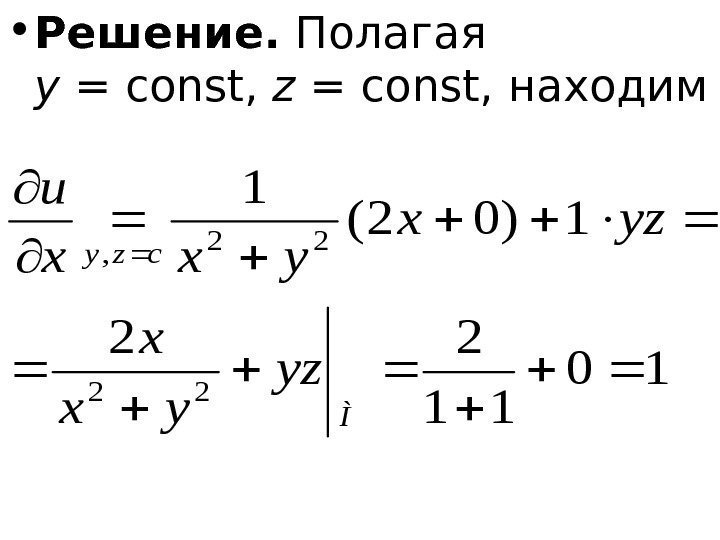
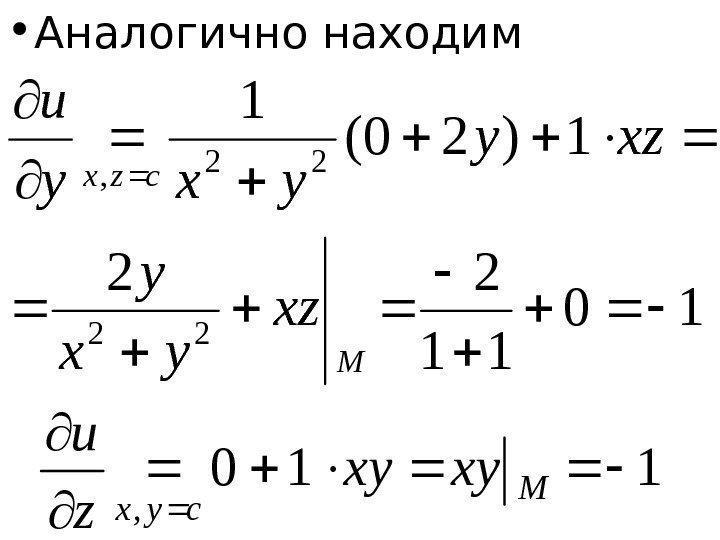








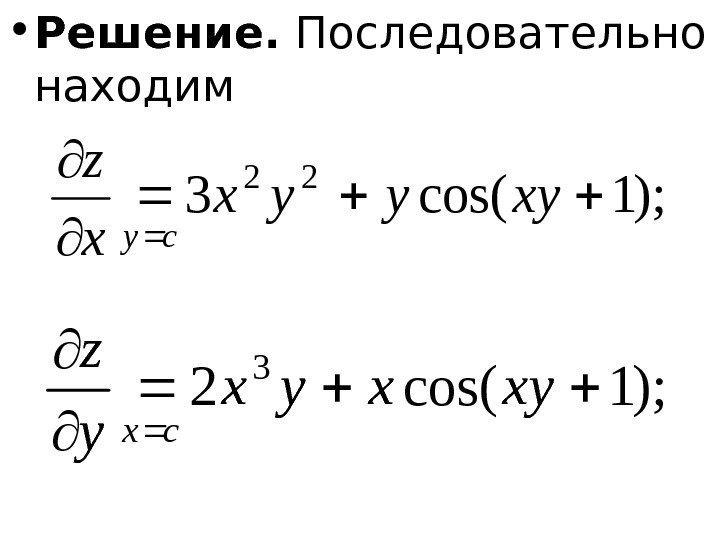
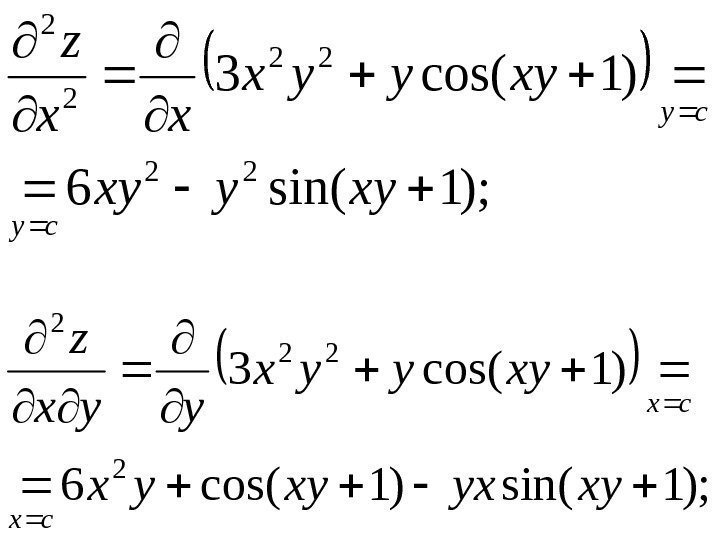
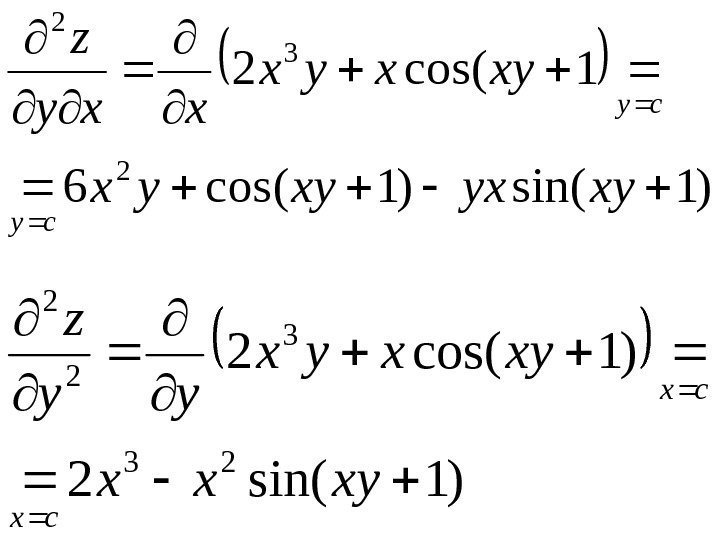


fnp_1.ppt
- Размер: 1.4 Мб
- Автор:
- Количество слайдов: 72
Описание презентации ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Модуль 5 по слайдам
 ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Модуль
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Модуль
 § 1. Понятие функции двух переменных.
§ 1. Понятие функции двух переменных.
 • Пусть x , y – две независимые друг от друга переменные. Графически пару независимых переменных ( x , y ) можно представить как точку M ( x , y ) на плоскости x. Oy. Пусть D – некоторое множество точек M ( x , y ).
• Пусть x , y – две независимые друг от друга переменные. Графически пару независимых переменных ( x , y ) можно представить как точку M ( x , y ) на плоскости x. Oy. Пусть D – некоторое множество точек M ( x , y ).
 • Опр. Если каждой точке M ( x , y ) из множества D по некоторому закону f ставится в соответ — ствие вполне определенное действительное число z , то говорят, что z есть функция двух переменных x и y и пишут z = f ( x , y ) или z = f ( M ) , где M = M ( x , y ) – точка плоскости.
• Опр. Если каждой точке M ( x , y ) из множества D по некоторому закону f ставится в соответ — ствие вполне определенное действительное число z , то говорят, что z есть функция двух переменных x и y и пишут z = f ( x , y ) или z = f ( M ) , где M = M ( x , y ) – точка плоскости.
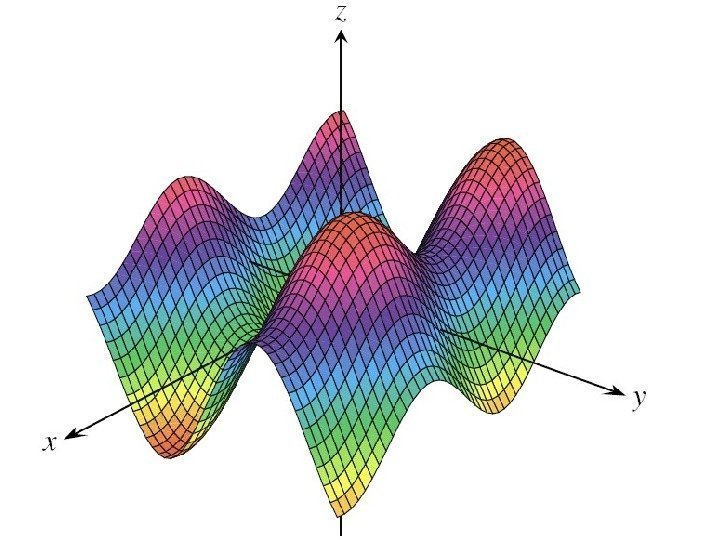
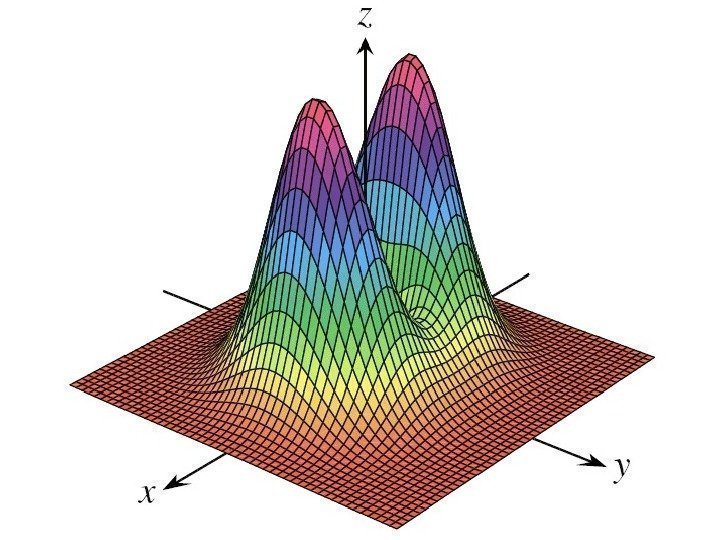
 • Геометрическим изображением функции двух переменных является некоторая поверхность в трехмерном пространстве.
• Геометрическим изображением функции двух переменных является некоторая поверхность в трехмерном пространстве.
 Примеры: • Г рафик функции • ( эллиптический параболоид )22 yxz
Примеры: • Г рафик функции • ( эллиптический параболоид )22 yxz
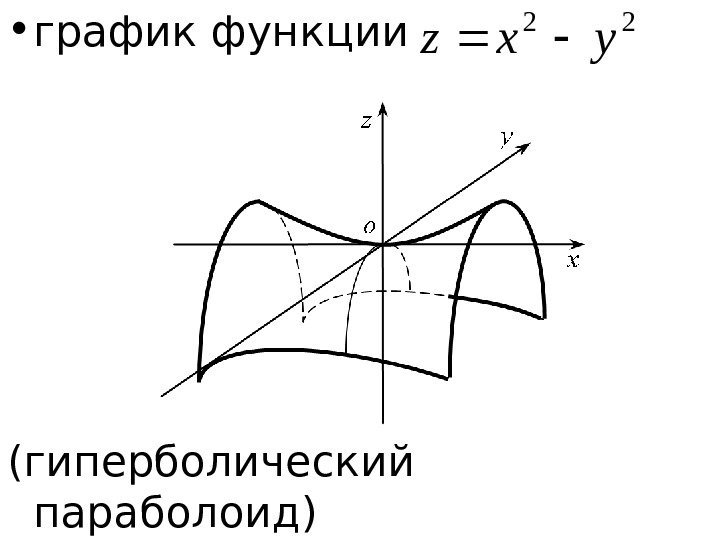
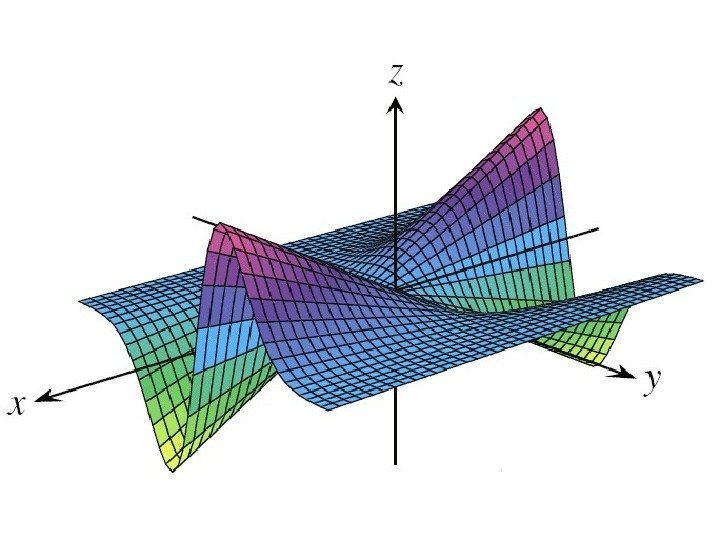
 • г рафик функции ( гиперболический параболоид )22 yxz
• г рафик функции ( гиперболический параболоид )22 yxz
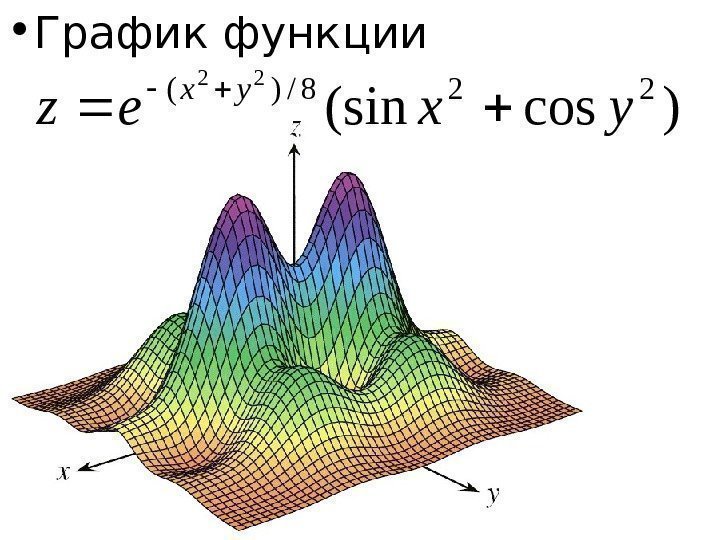
 • Г рафик функции )cos(sin 228/)( 22 yxez yx
• Г рафик функции )cos(sin 228/)( 22 yxez yx
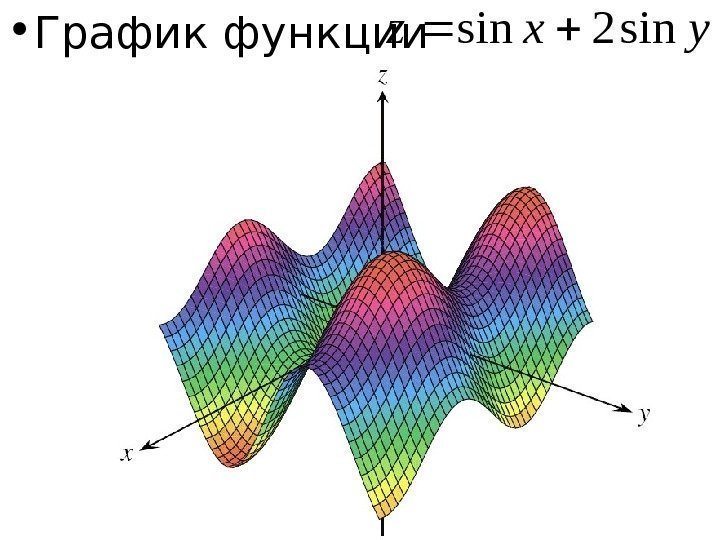
 • График функции yxzsin 2 sin
• График функции yxzsin 2 sin
 • Опр. Областью определения функции z = f ( x , y ) называется множество D точ е к M ( x , y ) , в которых функция z = f ( x , y ) определена и может быть вычислена. Все значения, которые принимает функция z = f ( x , y ) (в области ее определения), образуют множество значений функции.
• Опр. Областью определения функции z = f ( x , y ) называется множество D точ е к M ( x , y ) , в которых функция z = f ( x , y ) определена и может быть вычислена. Все значения, которые принимает функция z = f ( x , y ) (в области ее определения), образуют множество значений функции.
 Примеры
Примеры
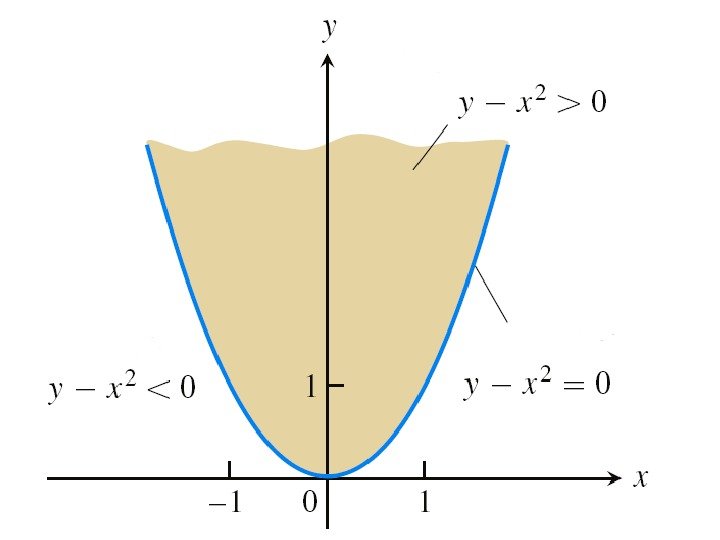
 Графическое изображение области определения функции. • Пример. Построим область определения функции 2 xyw
Графическое изображение области определения функции. • Пример. Построим область определения функции 2 xyw

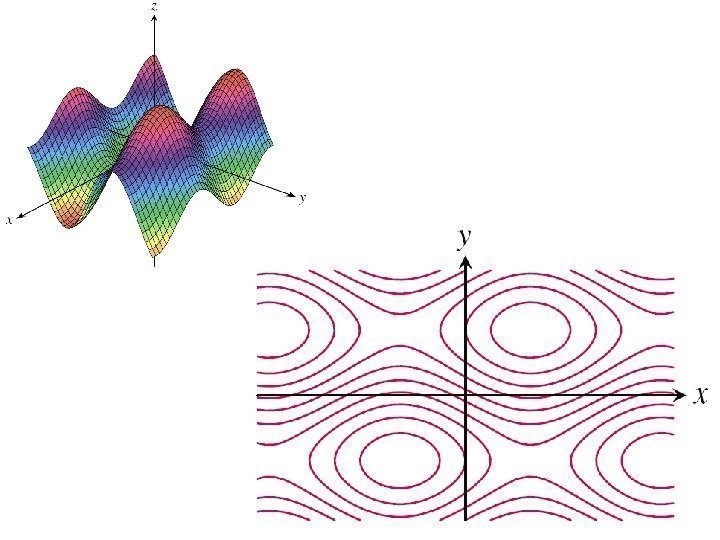
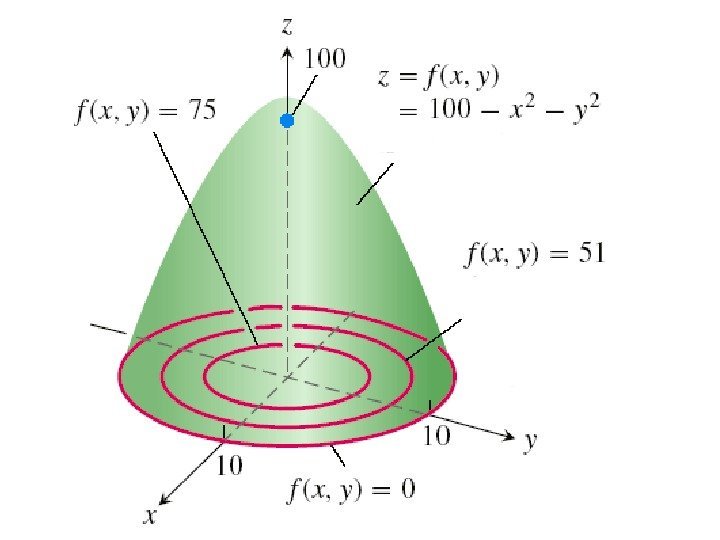
 Линии уровня • Опр. Множество точек плоскости таких, что функция f ( x , y ) принимает в них одно и то же значение, f ( x , y ) = c , называется линией уровня.
Линии уровня • Опр. Множество точек плоскости таких, что функция f ( x , y ) принимает в них одно и то же значение, f ( x , y ) = c , называется линией уровня.




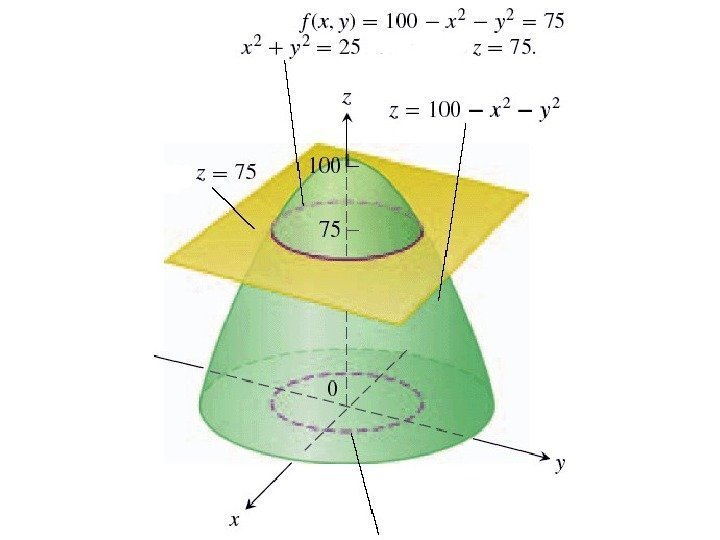
 Построение графика функции двух переменных • Рассмотрим пример построения графика функции 22 100), (yxyxf
Построение графика функции двух переменных • Рассмотрим пример построения графика функции 22 100), (yxyxf
 • Зафиксируем какое-нибудь значение этой функции, например, z = 75. Тем самым мы определили в пространстве плоскость z = 75. Находим линию уровня при z = 75: • 100– x 2 – y 2 =75, откуда x 2 + y 2 = 25 – уравнение окружности.
• Зафиксируем какое-нибудь значение этой функции, например, z = 75. Тем самым мы определили в пространстве плоскость z = 75. Находим линию уровня при z = 75: • 100– x 2 – y 2 =75, откуда x 2 + y 2 = 25 – уравнение окружности.

 • Находя множество линий уровня, строим весь график.
• Находя множество линий уровня, строим весь график.

 § 2. Понятие функции трех и более переменных. • Всякая упорядоченная совокупность действительных чисел ( x 1 , x 2 , …, x n ) называется точкой n –мерного пространства R n. Пусть D – некоторое мно-жество точек пространства R n.
§ 2. Понятие функции трех и более переменных. • Всякая упорядоченная совокупность действительных чисел ( x 1 , x 2 , …, x n ) называется точкой n –мерного пространства R n. Пусть D – некоторое мно-жество точек пространства R n.
 • Опр. Если каждой точке M ( x 1 , x 2 , …, x n ) из области D по некот о рому закону f ставится в сответствие вполне определенное число u , то говорят, что u есть функция n переменных и пишут u = f ( x 1 , x 2 , …, x n ) или u = f ( M ) где M = M ( x 1 , x 2 , …, x n ) – точка n –мерного пространства.
• Опр. Если каждой точке M ( x 1 , x 2 , …, x n ) из области D по некот о рому закону f ставится в сответствие вполне определенное число u , то говорят, что u есть функция n переменных и пишут u = f ( x 1 , x 2 , …, x n ) или u = f ( M ) где M = M ( x 1 , x 2 , …, x n ) – точка n –мерного пространства.
 Примеры
Примеры
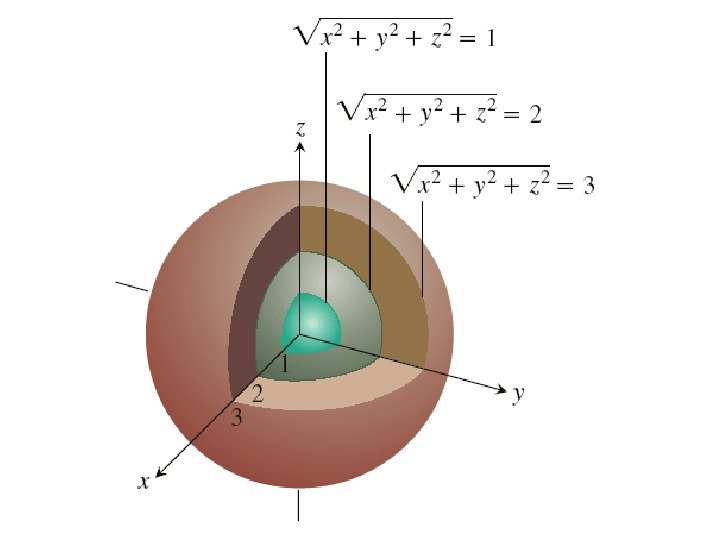
 • Опр. Множество точек пространства, в которых функция трех переменных f ( x , y , z ) принимает одно и то же значение, f ( x , y , z ) = c , называется поверхностью уровня.
• Опр. Множество точек пространства, в которых функция трех переменных f ( x , y , z ) принимает одно и то же значение, f ( x , y , z ) = c , называется поверхностью уровня.

 § 3. Предел и непрерывность функции нескольких переменных
§ 3. Предел и непрерывность функции нескольких переменных
 • Опр. Число A называется пределом функции z = f ( x , y ) в точке M 0 ( x 0 , y 0 ), если для каждого числа ε > 0 найдется такое число δ = δ(ε), что при 0 < | x – x 0 | < δ и 0 < | y – y 0 | < δ выполняется неравенство | f ( x , y ) – A | < ε. При этом пишут)(lim), (lim 0 0 0 Mfyxf. A MM yy xx
• Опр. Число A называется пределом функции z = f ( x , y ) в точке M 0 ( x 0 , y 0 ), если для каждого числа ε > 0 найдется такое число δ = δ(ε), что при 0 < | x – x 0 | < δ и 0 < | y – y 0 | < δ выполняется неравенство | f ( x , y ) – A | < ε. При этом пишут)(lim), (lim 0 0 0 Mfyxf. A MM yy xx
 • Опр. Функция z = f ( x , y ) называется непрерывной в точке M 0 ( x 0 , y 0 ), если функция z = f ( x , y ) определена в этой точке и существует ). , (), (lim 00 0 0 yxfyxf yy xx
• Опр. Функция z = f ( x , y ) называется непрерывной в точке M 0 ( x 0 , y 0 ), если функция z = f ( x , y ) определена в этой точке и существует ). , (), (lim 00 0 0 yxfyxf yy xx
 • Аналогичные определения имеют место и для функции u = f ( x 1 , x 2 , …, x n ) в случае произвольного числа n переменных.
• Аналогичные определения имеют место и для функции u = f ( x 1 , x 2 , …, x n ) в случае произвольного числа n переменных.
 • Если в какой – либо точке условие непрерывности не выполняется, то эта точка называется точкой разрыва функции f ( x , y ). Это может быть в следующих случаях:
• Если в какой – либо точке условие непрерывности не выполняется, то эта точка называется точкой разрыва функции f ( x , y ). Это может быть в следующих случаях:
 • 1. Функция z = f ( x , y ) не определена в точке M 0 ( x 0 , y 0 ). • 2. Не существует предел • 3. Этот предел существует, но он не равен f ( x 0 , y 0 ). ), (lim 0 0 yxf yy xx
• 1. Функция z = f ( x , y ) не определена в точке M 0 ( x 0 , y 0 ). • 2. Не существует предел • 3. Этот предел существует, но он не равен f ( x 0 , y 0 ). ), (lim 0 0 yxf yy xx
 § 4. Частные производные функции нескольких переменных
§ 4. Частные производные функции нескольких переменных









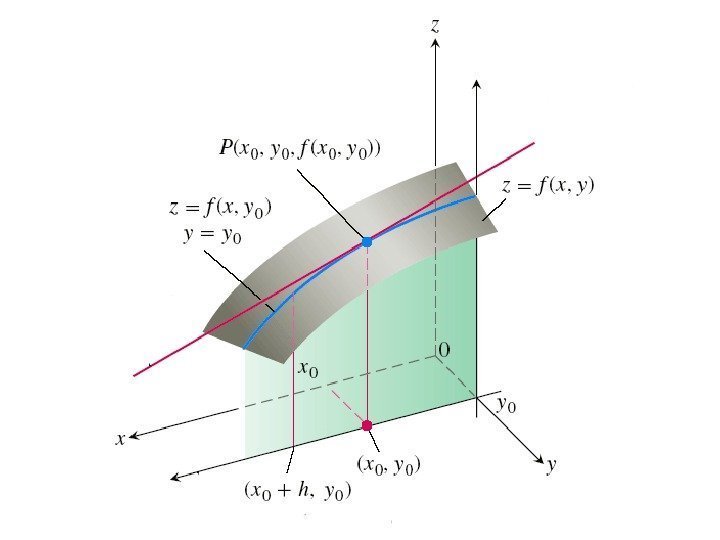
 • Пусть z = f ( x , y ) – функция двух переменных. Дадим независимой переменной x приращение Δ x , оставляя при этом переменную y неизменной. Тогда функция z получит приращение которое называется частным приращением z по x. ), (yxfyxxfz x
• Пусть z = f ( x , y ) – функция двух переменных. Дадим независимой переменной x приращение Δ x , оставляя при этом переменную y неизменной. Тогда функция z получит приращение которое называется частным приращением z по x. ), (yxfyxxfz x
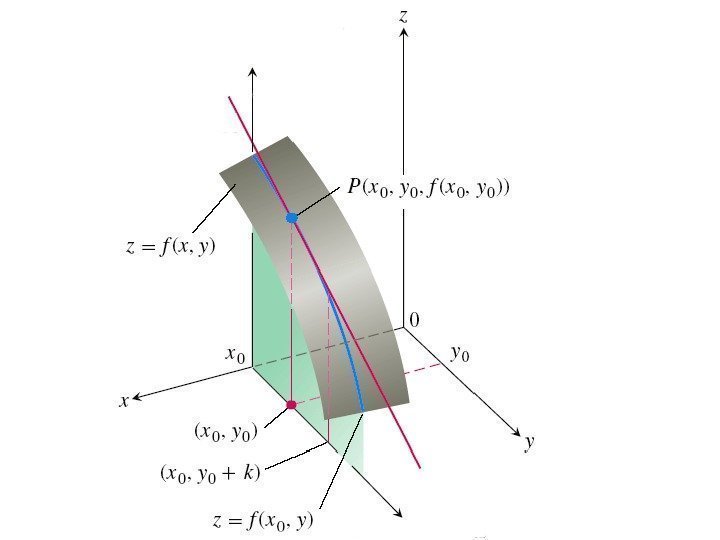
 • Аналогично, если независимой переменной y дадим приращение Δ y , оставляя при этом неизменной переменную x , то функция z получит приращение называемое частным приращением z по y. ), , (), (yxfyyxfzy
• Аналогично, если независимой переменной y дадим приращение Δ y , оставляя при этом неизменной переменную x , то функция z получит приращение называемое частным приращением z по y. ), , (), (yxfyyxfzy
 • Опр. Частной производной по x от функции z называется предел отношения частного приращения Δ x z к приращению Δ x при стремлении Δ x к нулю. • Эта производная обозначается одним из символов). , (, , , yxf x f z xx
• Опр. Частной производной по x от функции z называется предел отношения частного приращения Δ x z к приращению Δ x при стремлении Δ x к нулю. • Эта производная обозначается одним из символов). , (, , , yxf x f z xx
 Таким образом, по определению, x yxfyxxf x z x x x ), ( limlim
Таким образом, по определению, x yxfyxxf x z x x x ), ( limlim
 • Аналогично определяется частная производная от функ-ции z = f ( x , y ) по переменной y : Обозначается одним из символовy yxfyyxf y z y y y ), ( limlim 00 ). , (, , , yxf y f z yy
• Аналогично определяется частная производная от функ-ции z = f ( x , y ) по переменной y : Обозначается одним из символовy yxfyyxf y z y y y ), ( limlim 00 ). , (, , , yxf y f z yy
 • В общем случае частной производной первого порядка функции u = f ( x 1 , x 2 , …, x n ) по переменной x k называется пределk nknkk x xxxfxxxxf x u k k k ), , , , ( lim
• В общем случае частной производной первого порядка функции u = f ( x 1 , x 2 , …, x n ) по переменной x k называется пределk nknkk x xxxfxxxxf x u k k k ), , , , ( lim
 • Т. к. при вычислении частных производных все переменные, кроме одной, считают постоянными, то для частных производных сохранаяются все правила и формулы дифференцирования функции одной переменной.
• Т. к. при вычислении частных производных все переменные, кроме одной, считают постоянными, то для частных производных сохранаяются все правила и формулы дифференцирования функции одной переменной.
 • Пример. Найти частные производные функции y x yxz
• Пример. Найти частные производные функции y x yxz
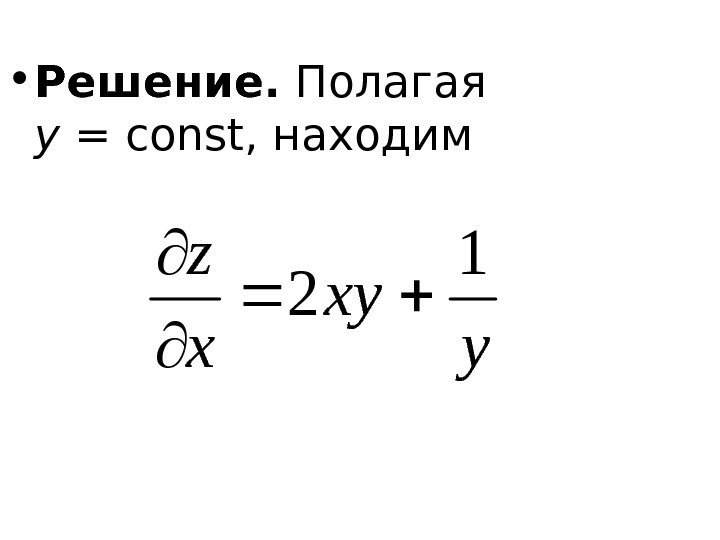 • Решение. Полагая y =const , находимy xy x z
• Решение. Полагая y =const , находимy xy x z
 • Полагая x =const , находим 2 2 ) 1 (1 y x x y xx y z
• Полагая x =const , находим 2 2 ) 1 (1 y x x y xx y z
 • Пример. Найти значения частных производных функции в точке M (1, – 1, 0). xyzyxu)ln(
• Пример. Найти значения частных производных функции в точке M (1, – 1, 0). xyzyxu)ln(
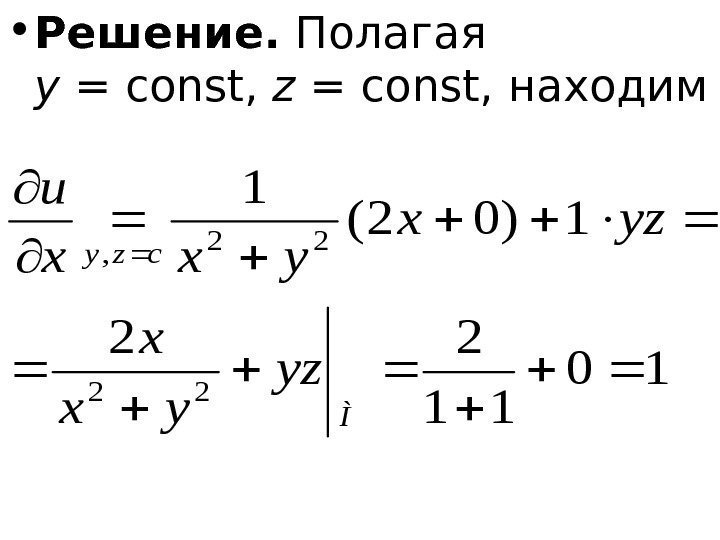 • Решение. Полагая y = const , z = const , находим 10 11 22 1)02( 1 22 22 , Ì czy yz yx x yzx yxx u
• Решение. Полагая y = const , z = const , находим 10 11 22 1)02( 1 22 22 , Ì czy yz yx x yzx yxx u
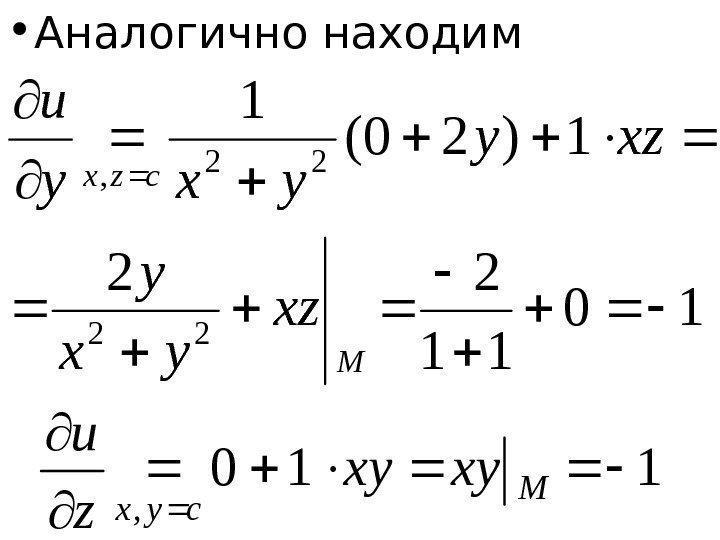 • Аналогично находим 10 11 22 1)20( 1 22 22 , M czx xz yx y xzy yxy u 110 , M cyx xyxy z u
• Аналогично находим 10 11 22 1)20( 1 22 22 , M czx xz yx y xzy yxy u 110 , M cyx xyxy z u
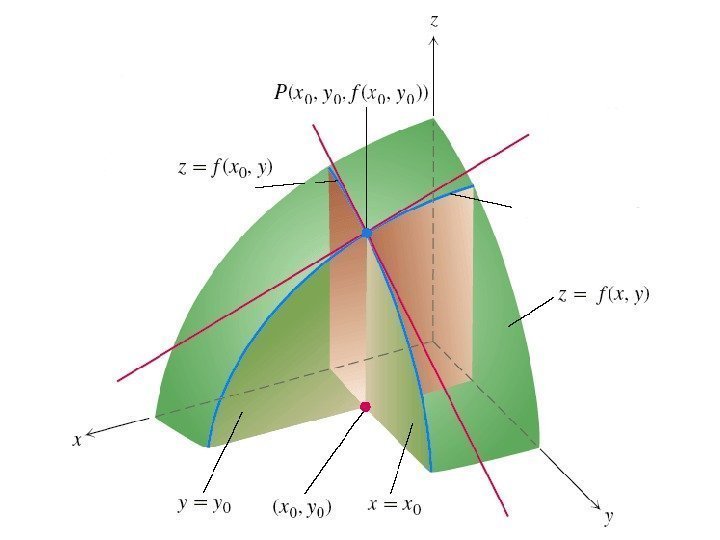
 • Предположим, что функция z = f ( x , y ) имеет непрерывные частные производные), (yxf x z x ), (yxf y z y
• Предположим, что функция z = f ( x , y ) имеет непрерывные частные производные), (yxf x z x ), (yxf y z y
 • Эти производные в свою очередь являются функциями независимых переменных x и y. Будем называть и частными производными 1 — го порядка. ), (yxf x ), (yxf y
• Эти производные в свою очередь являются функциями независимых переменных x и y. Будем называть и частными производными 1 — го порядка. ), (yxf x ), (yxf y
 • Частными производными 2 -го порядка называются частные производные от частных производных 1 -го порядка. • Для функции z = f ( x , y ) двух переменных можно найти четыре частные производные 2 -го порядка, которые обозна-чаются следующим обр-м:
• Частными производными 2 -го порядка называются частные производные от частных производных 1 -го порядка. • Для функции z = f ( x , y ) двух переменных можно найти четыре частные производные 2 -го порядка, которые обозна-чаются следующим обр-м:

 • В общем случае смешанные частные производные могут не совпадать, однако для них справедлива теорема: • Теорема. Если смешанные частные производные и непрерывны в некоторой точке M ( x , y ) , то они равны, т. е. xyfyxf ), (yxfyxf yxxy
• В общем случае смешанные частные производные могут не совпадать, однако для них справедлива теорема: • Теорема. Если смешанные частные производные и непрерывны в некоторой точке M ( x , y ) , то они равны, т. е. xyfyxf ), (yxfyxf yxxy
 • Ч астными производными n – го порядка называются частные производные от частных производных ( n – 1)– го порядка. • Их обозначают и т. д. 221 , , yx z x z n n n
• Ч астными производными n – го порядка называются частные производные от частных производных ( n – 1)– го порядка. • Их обозначают и т. д. 221 , , yx z x z n n n
 • Частные производные любого порядка, взятые по различным переменным, называются смешанными.
• Частные производные любого порядка, взятые по различным переменным, называются смешанными.
 • Пример. Найти частные производные 2 -го порядка функции )1 sin( 23 xyyxz
• Пример. Найти частные производные 2 -го порядка функции )1 sin( 23 xyyxz
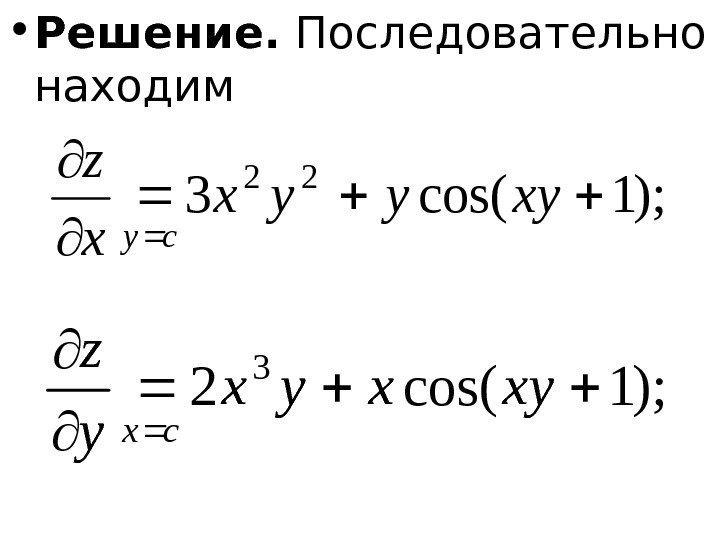 • Решение. Последовательно находим); 1 cos(3 22 xyyyx x z cy ); 1 cos(2 3 xyxyx y z cx
• Решение. Последовательно находим); 1 cos(3 22 xyyyx x z cy ); 1 cos(2 3 xyxyx y z cx
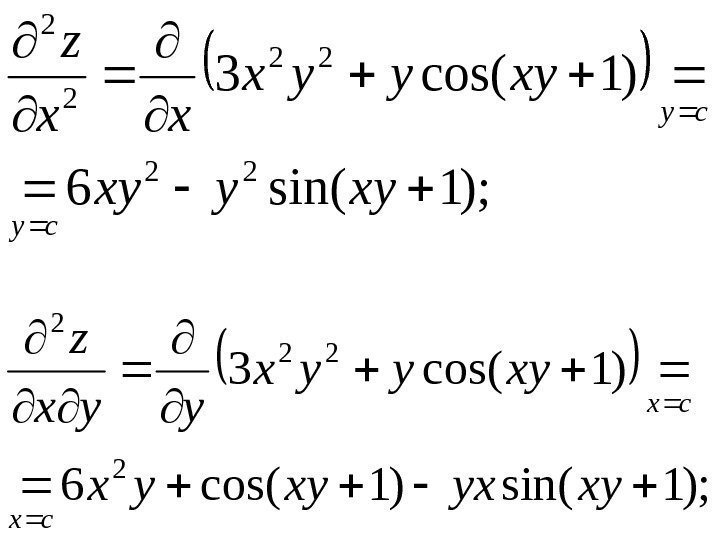 ); 1 sin(6 )1 cos(3 22 22 2 2 xyyxy xyyyx xx z cy cy ); 1 sin()1 cos(6 )1 cos(3 2 22 2 xyyx xyyyx z cx cx
); 1 sin(6 )1 cos(3 22 22 2 2 xyyxy xyyyx xx z cy cy ); 1 sin()1 cos(6 )1 cos(3 2 22 2 xyyx xyyyx z cx cx
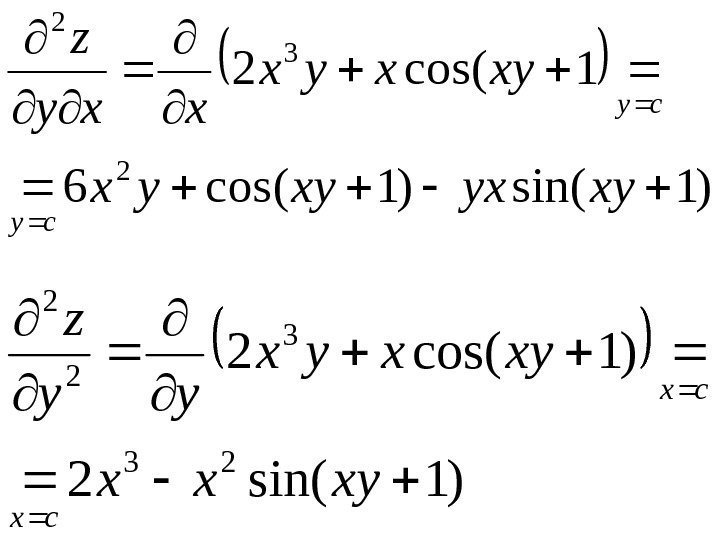 )1 sin()1 cos(6 1 cos(2 2 3 2 xyyx xyxyx xxy z cy cy )1 sin(2 )1 cos(2 23 3 2 2 xyxx xyxyx yy z cx cx
)1 sin()1 cos(6 1 cos(2 2 3 2 xyyx xyxyx xxy z cy cy )1 sin(2 )1 cos(2 23 3 2 2 xyxx xyxyx yy z cx cx




