ДИФФЕРЕНЦИАЛ ФУНКЦИИ Определение дифференциала функции и его геометрический

ДИФФЕРЕНЦИАЛ ФУНКЦИИ Определение дифференциала функции и его геометрический смысл. Основные теоремы о дифференциалах. Применение дифференциала к приближенным вычислениям. Дифференциалы высших порядков.

Вопрос 1. Определение дифференциала функции и его геометрический смысл Пусть функция у = f(х) дифференцируема в точке х, т.е. имеет в этой точке конечную производную На основании теоремы о связи бесконечно малых функций и пределов можно записать (1)

где α(Δх) - бесконечно малая функция при Δх→0, т.е. Умножая обе части равенства (1) на Δх, получим Δу = у′Δх + α(Δх)Δх. (2) Пусть у′ = f′(х)  0. Тогда из равенства (2) следует, что приращение функции Δу представляет собой сумму двух слагаемых - у′Δх и α(Δх)Δх, являющихся бесконечно малыми функциями при Δх→0.

Сравним каждое из них с Δу.

Поэтому первое слагаемое у′Δх называют главной частью приращения функции Δу. О.1.1. Дифференциалом функции у = f(х) в точке х называется главная (линейная относительно Δх) часть ее приращения в данной точке. Обозначение: dу или df(х). По определению dу = у′Δх или dу = f′(х)Δх (3)

Пусть у = х, тогда dу = dх = х′Δх = Δх  дифференциал независимой переменной х равен приращению данной переменной, т.е. dх = Δх Формулы (3) примут вид dу = у′dх или dу = f′(х)dх (4) Таким образом, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Пример 1. Найти дифференциал функции у = х3 ‒ х2 + 3х ‒ 1. Решение

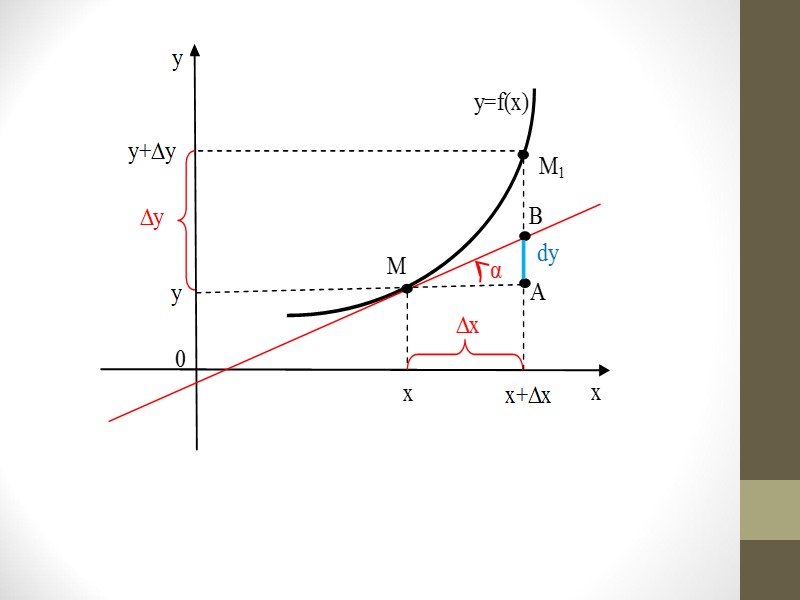
1.2. Геометрический смысл дифференциала Пусть М(х,у) и М1(х+∆х,у+∆у) - две точки графика функции у = f(х). Проведем в точке М касательную МВ к графику функции и рассмотрим прямоугольный треугольник ΔМВА. Если обозначить угол наклона касательной МВ к оси Ох через α, то ВМА = α и АВ = АМ·tgα = Δх·tgα. Но tgα = у′, поэтому АВ = у′Δх = dу.

Таким образом, дифференциал функции у = f(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получает приращение Δх.

Вопрос 2.Основные теоремы о дифференциалах Т.2.1.Дифференциал постоянной С равен нулю, т.е. dС = 0 Доказательство Если у = С, то ч.т.д.

Т.2.2. Дифференциалы алгебраической суммы, произведения и частного двух дифференцируемых функций u = u(х) и v = v(х) определяются следующими формулами:

Доказательство Докажем, например, вторую формулу: Остальные формулы доказываются аналогично (доказать самостоятельно). ч.т.д. Следствие Постоянный множитель можно выносить за знак дифференциала, т.е.

Т.2.3. (инвариантность формы первого дифференциала) Дифференциал сложной функции равен производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента. Доказательство Пусть у = f(u) и u = φ(х) - две дифференцируемые функции, образующие сложную функцию у = f(φ(х)). По правилу дифференцирования сложной функции имеем

Умножив обе части этого равенства на dх, получим Отсюда (5) ч.т.д.

Сравнивая формулы (4) и (5), можно увидеть, что дифференциал функции определяется одной и той же формулой независимо от того, является ли ее аргумент независимой переменной или является функцией другого аргумента. Это свойство дифференциала называется инвариантностью (неизменностью) формы дифференциала.

Замечание Формула (4) (dу = у′dх) по внешнему виду совпадает с формулой (5) , но между ними есть принципиальное отличие: в (4) х – независимая переменная, следовательно, dх = Δх; в (5) u ‒ функция от х, поэтому, вообще говоря, du  Δu.

Пример 2. С помощью определения дифференциала и основных теорем о дифференциалах легко преобразовать таблицу производных в таблицу дифференциалов Пример 3.

Вопрос 3. Применение дифференциала к приближенным вычислениям Рассмотрим равенство (2): Δу = у′Δх + α(Δх)Δх. Перепишем данное равенство с учетом того, что dу = у′Δх. Тогда получим соотношение Δу = dу + α(Δх)Δх. (6) Отбрасывая бесконечно малую α(Δх)Δх более высокого порядка, чем Δу, получаем из (6) приближенное равенство Δу ≈ dу, (7) причем это равенство тем точнее, чем меньше Δх.

Так как ∆у = f(х+∆х) ‒ f(х) и dу = f′(х)Δх, то равенство (7) можно переписать в другой форме f(х+∆х) ‒ f(х) ≈ f′(х)Δх или f(х+∆х) ≈ f′(х)Δх + f(х) (8) Формула (8) используется для вычисления приближенных значений функции.

Пример 4. Найти приближенное значение sin460. Решение

Вопрос 4. Дифференциалы высших порядков Пусть у = f(х) - дифференцируемая функция, где х - независимая переменная. Ее дифференциал dу = f′(х)dх есть функция от двух аргументов - х и dх. Будем рассматривать dх в выражении для dу как постоянный множитель. Тогда dу есть функция аргумента х и можно найти дифференциал данной функции. Дифференциал dу называется дифференциалом первого порядка или первым дифференциалом функции у = f(х).

О.4.1. Дифференциал от первого дифференциала функции у = f(х) называется дифференциалом второго порядка или вторым дифференциалом данной функции и обозначается d2у или d2f(х), т.е. Найдем выражение второго дифференциала функции у = f(х). Так как dх = Δх не зависит от х, то при дифференцировании считаем dх постоянным:

т.е. О.4.2. Дифференциал от второго дифференциала функции у = f(х) называется дифференциалом третьего порядка или третьим дифференциалом данной функции и обозначается d3у или d3f(х), т.е. Аналогично можно показать, что Дифференциалы, начиная со второго, называются дифференциалами высших порядков.

О.4.3. Дифференциал от (n‒1)-го дифференциала функции у = f(х) называется дифференциалом n-го порядка или n-м дифференциалом данной функции и обозначается dnу или dnf(х), т.е. При этом справедлива формула (9)

Пользуясь дифференциалами, производную любого порядка можно представить в виде отношения соответствующих дифференциалов: (10) Замечание Равенства (9) и (10) при n > 1справедливы только, если х – независимая переменная, т.е. дифференциалы высших порядков не обладают свойством инвариантности формы, в отличие от дифференциала первого порядка.