Дифференциал функции двух переменных Таким же важным, как

Дифференциал функции двух переменных

Таким же важным, как и понятие производной в математическом анализе, является и понятие дифференциала функции.

Вернемся к определению производной: Lim ∆y/∆x = y’ ∆x∞ (предел отношения бесконечно) малого приращения функции к бесконечно малому приращению аргумента. Мы знаем, что переменная величина, имеющая предел, может быть представлена в виде суммы этого предела и бесконечно малой: ∆y/∆x=y’+α (1) , где α - бесконечно малая

Отсюда имеем, ∆y=(y,+α ) ∆x=y,× ∆x+a×∆ x. Эта формула определяет связь между приращением ∆y всякой дифференцируемой функции y=f(x) и приращением ее аргумента ∆x. Величина α- бесконечно мала одновременно с ∆x: lim α = 0 Поэтому, второе слагаемое α ×∆ x будет бесконечно малой более высокого порядка, чем ∆x (как произведение двух бесконечно малых ∆x и α); в то же время, как первое слагаемое y/∆x будет бесконечно малой того же порядка, что и ∆ x (если только y≠0 при данном значении аргумента x).

Таким образом, формула определяет бесконечно малое приращение ∆y дифференцируемой функции y (при y≠0) в виде суммы двух слагаемых: одного (y,∆x) – того же порядка малости, что и ∆ x; другого (α×∆ x) – более высокого порядка малости. Поэтому первое слагаемое y,∆x будет главной частью приращения функции ∆ y.

Определение. Эту главную часть приращения функции, пропорциональную приращению аргумента, называют дифференциалом функции и обозначают символом dy: dy=y,*∆ x (2) Применив эту формулу к функции y=x, получим dy=dx=1*∆x=∆x.Поэтому, естественно под дифференциалом аргумента функции понимать приращение dx=∆x, то есть под символом dx понимают и приращение аргумента, и дифференциал функции, равной аргументу.

Теперь, формулу (2) можно записать dy=y,*dx (3), а формулу (1) в виде ∆y=y,*dx+α*dx (4). Итак, установлено: 1) Дифференциал функции равен произведению ее производной на дифференциал аргумента (независимой переменной). 2) Разность между приращением функции ∆y и ее дифференциалом dy есть величина бесконечно малая более высокого порядка малости, чем приращение аргумента ∆ x, а также (при y≠0) более высокого порядка, чем приращение функции ∆y и ее дифференциал dy. 3) Приращение функции ∆ y и ее дифференциал dy при бесконечно малом ∆ x являются равносильными бесконечно малыми dy~∆y (5).

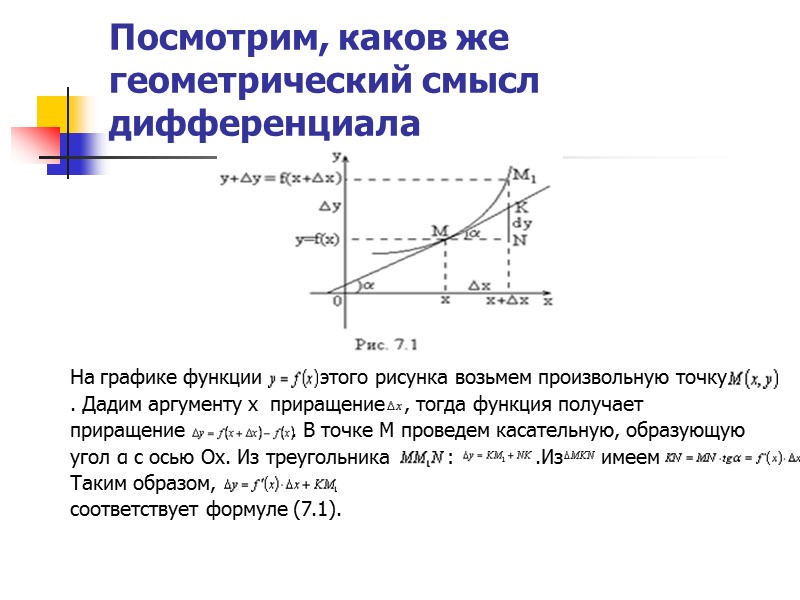
Посмотрим, каков же геометрический смысл дифференциала На графике функции этого рисунка возьмем произвольную точку . Дадим аргументу x приращение , тогда функция получает приращение . В точке М проведем касательную, образующую угол α с осью Ox. Из треугольника : .Из имеем Таким образом, соответствует формуле (7.1).

Следовательно, с геометрической точки зрения дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y=f(x) в данной точке, когда х получает приращение ∆x Дифференциал функции двух переменных Пусть функция z = f(x,y), имеет в точке М0(х0,у0) частные производные f /x (х0,у0) и f /у (х0,у0). О. Полным приращением функции z = f(x,y) в точке М0(х0,у0) называется разность Пусть приращение функции z =f(x,y) можно представить в виде где функция называется дифференцируемой в точке M 0 (х0,у0).

Полным дифференциалом функции z=f(x,y) называется главная часть полного приращения, линейная относительно приращений её аргументов.Полный дифференциал функции (если он существует) равен сумме всех ее частных дифференциалов и вычисляется по формуле: При достаточно малых (по абсолютному значению) приращениях аргументов, полное приращение функции можно с как угодно малой относительной погрешностью заменить ее полным дифференциалом. Дифференциалы dх и dy независимых аргументов функции ∆х и ∆у совпадают с их приращениями соответственно . Таким образом,

Презентацию выполнила студентка 1 курса факультета менеджмента Шутова Виктория Группа 1150

Спасибо за внимание !