«Численные методы решения нелинейных уравнений» 612)(

«Численные методы решения нелинейных уравнений»

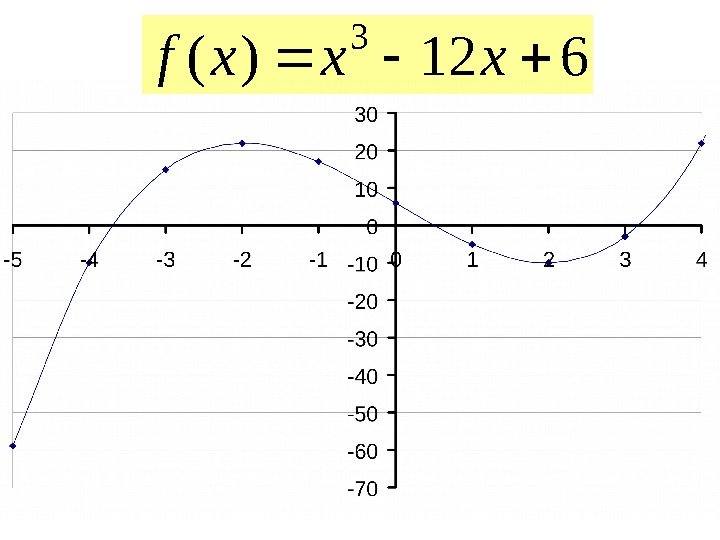
612)( 3 xxxf

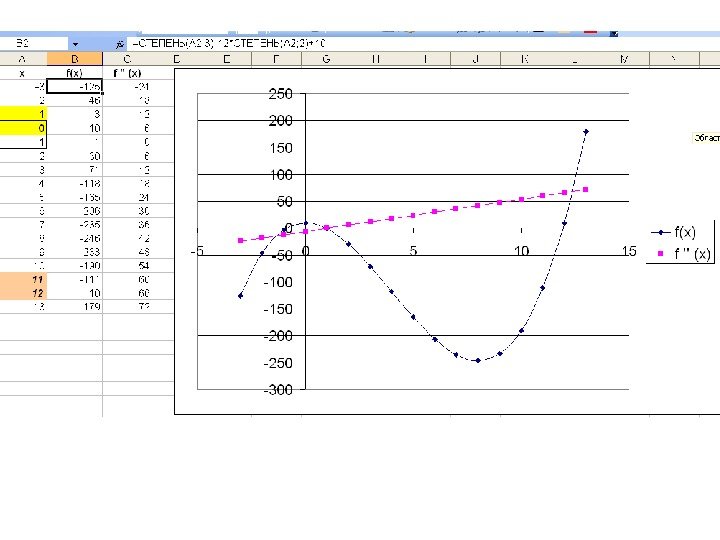
находим первую производную612)( 3 xxxf находим корни первой производной 123)( 2 xxf 2 2 21 x x

составляем таблицу знаков функции: x — -2 2 + знак f(x) ; 2 2; 3 2 1 x x x Уменьшим интервалы, содержащие корни так, чтобы их длина была не более 1 — ++ — 612)( 3 xxxf

x -4 -3 -2 -1 0 1 2 3 4 знак f(x) 4; 3 1; 0 3; 4 3 2 1 x x x -+ + ++ — — +

Волжский институт строительства и технологий (филиал) Волгоградского государственного архитектурно-строительного университета Типовой расчет № 2 «Численные методы решения нелинейных уравнений» Выполнил студент гр. СДМ-2 -08 Иванович Проверил: доц. Байдакова Н. В. Волжский

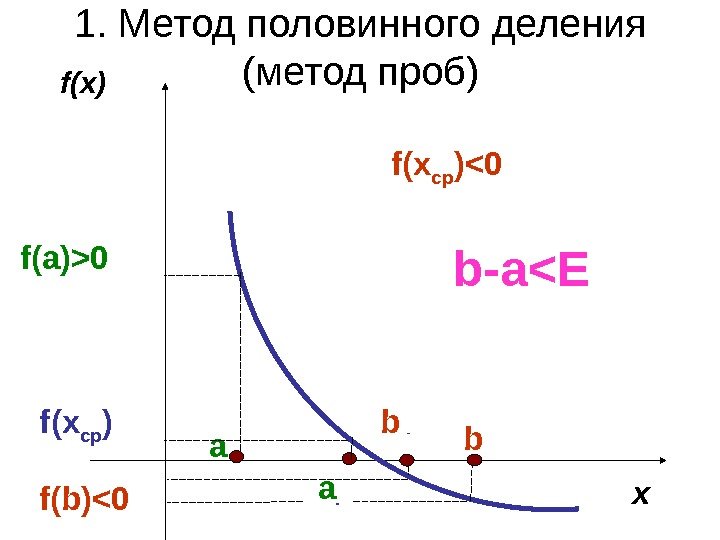
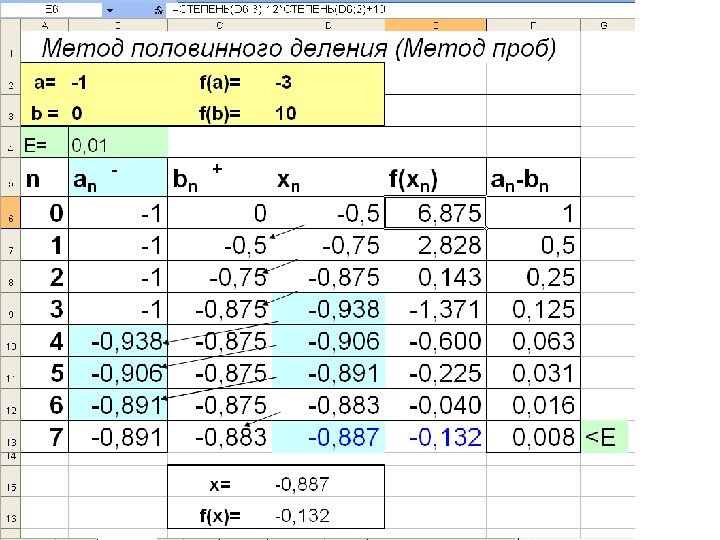
1. Метод половинного деления (метод проб) bf(x) x срaf ( a)>0 f ( b)0 f ( x cp )<0 b b-a<

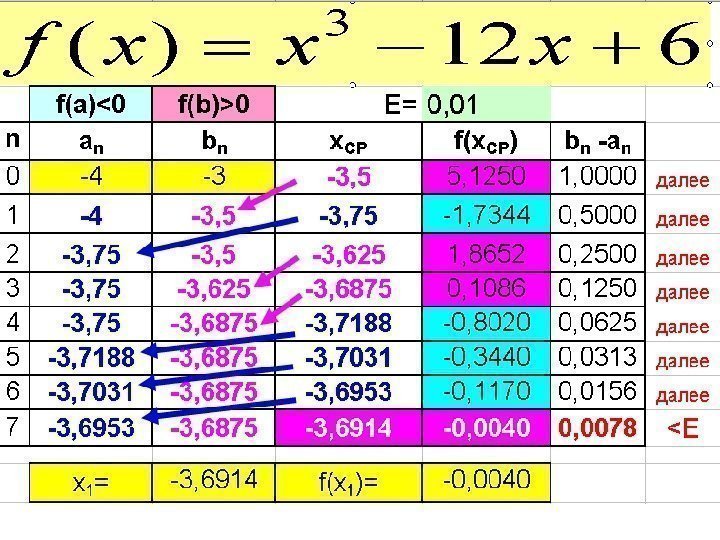
Выберем отрезок [a; b] так, чтобы f(a)*f(b)<0 1. Вычисляем f(x. СР ) где 2 ba x CP 2. Если f(x СР ) =0 то задача решена. 3. Если f(x СР ) ≠ 0 то из двух отрезков [a; x СР ] и [x СР ; b] выбираем тот, на концах которого функция принимает значения разных знаков. 4. Если b-a ≤ E вычисления прекращаем , Иначе переходим к п. 1. Принимаем E 1=0,

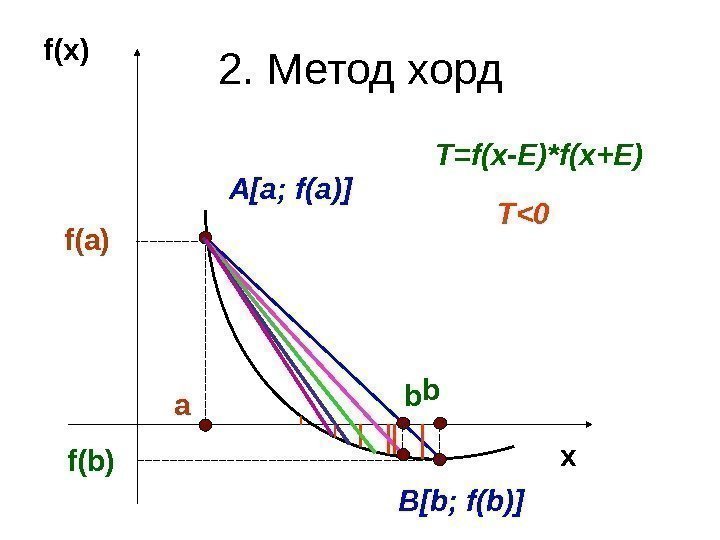
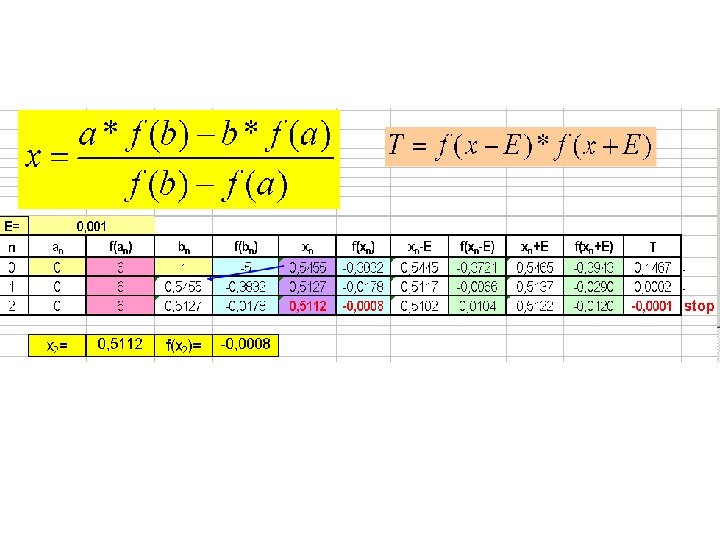
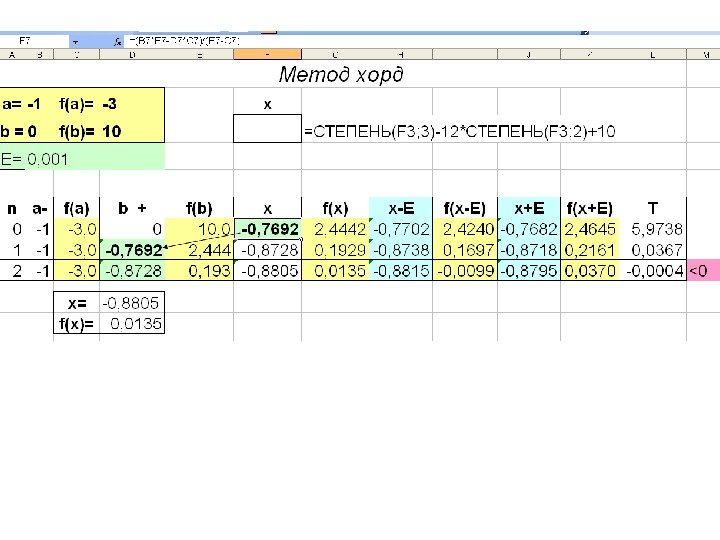
2. Метод хорд x bf(x) a xf ( a) f ( b) A[a; f(a)] B[b; f(b)] T=f(x-E)*f(x+E) T>0 b T<

Выберем отрезок [a; b] так, чтобы f(a)*f(b)<0 1. Проведем хорду, соединяющую точки A[a; f(a)] и B[b; f(b)] 2. Точка пересечения хорды с осью ох : )()( )(*)(* afbf afbbfa x 3. Вычисляем величину: )(*)(Exf. T 4. Если T <0 то задача решена. 5. Иначе из двух отрезков [a; x] и [x; b] выбираем тот, на концах которого функция принимает значения разных знаков. и переходим к пункту 1 Принимаем E 2=0,

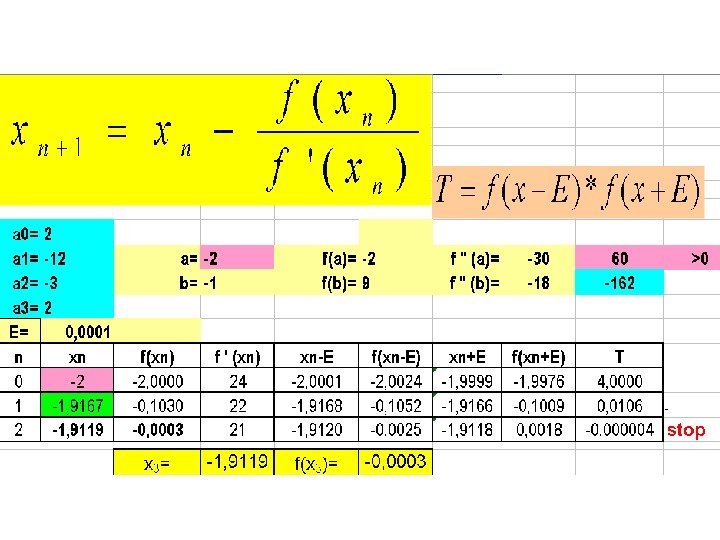
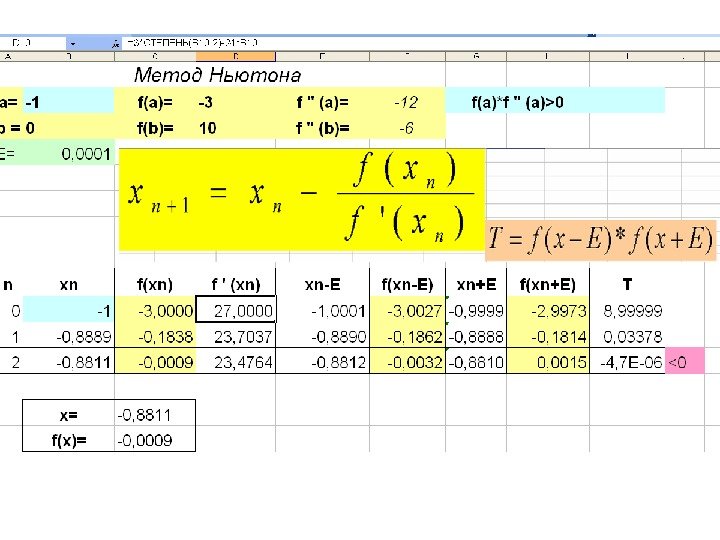
3. Метод касательных (Ньютона) B[b; f(b)] bf(x) a xf ( a) f ( b) A[a; f(a)]0)(*)( 00 xfxf x 0 x 1 0 T

Выберем отрезок [a; b] так, чтобы f(a)*f(b)<0 f ‘‘ (x) определена и на концах отрезка не меняет свой знак. 1. Из двух концов отрезка [a; b] выберем тот, для которого выполняется неравенство: 0)(*)(00 xfxf и проведем касательную к графику функции в этой точке. 2. Точка пересечения касательной с осью ох : Вычисляем величину: )(*)(11 Exf. Tnn 3. Если T <0 то задача решена. 4. Иначе из двух отрезков [a; x] и [x; b] выбираем тот, на концах которого функция принимает значения разных знаков и переходим к пункту 2 Принимаем E 3=0, 0001 )( )( 1 n n nn xf xf xx

Министерство образования и науки РФ Волжский политехнический институт (филиал) Волгоградского государственного технического университета Типовой расчет № 1 «Численные методы решения нелинейных уравнений» Выполнил студент гр. ВСТ-123 Иванович Проверил: доц. Байдакова Н. В. Волжский