ЧИСЛЕННЫЕ МЕТОДЫ Методы решения нелинейных уравнений Лекция 4:

ЧИСЛЕННЫЕ МЕТОДЫ Методы решения нелинейных уравнений Лекция 4:

Комбинированный метод хорд и касательных. Метод хорд и метод касательных часто применяют в сочетании друг с другом. Пусть дано уравнение f(x)=0, корень t отделен и находится на отрезке [a, b]. Применим комбинированный метод хорд и касательных. 2

Комбинированный метод хорд и касательных. Если и f (x)>0, то метод хорд дает приближение корня с недостатком, а метод касательных с избытком. 3

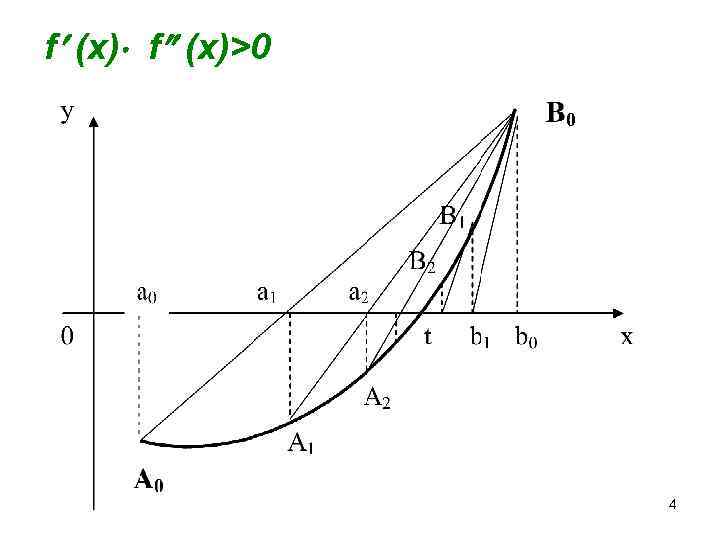f (x)>0 4

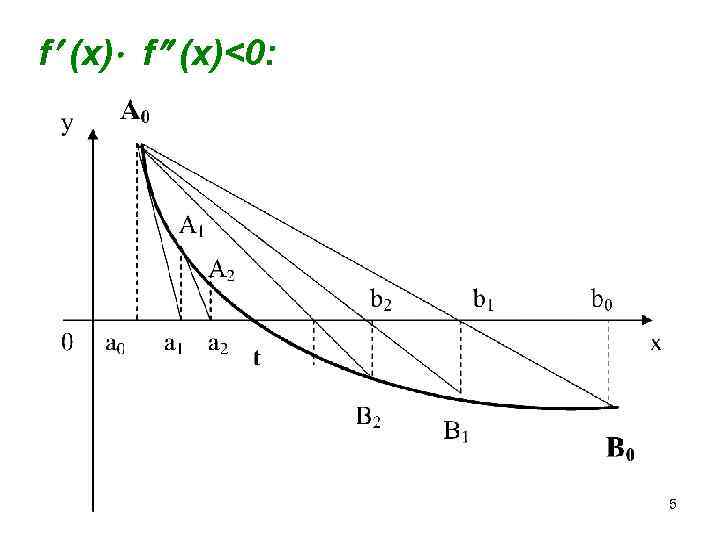f (x)<0: 5

Комбинированный метод хорд и касательных. • Если f (x)>0: • Если f (x)<0: 6

Комбинированный метод хорд и касательных. • Процесс вычислений прекращается, как только станет выполняться неравенство: • Приближенное значение корня: 7

Метод итераций l 8 Заменим уравнение f(x)=0 равносильным ему –x= (x). Требуется найти вещественный корень этого уравнения на отрезке [a, b]. Возьмем произвольную точку x 0 из области определения функции (x) и будем строить последователь-ность чисел с помощью рекуррентной формулы xn+1= (xn), т. е. x 1= (x 0), x 2= (x 1), x 3= (x 2) и т. д.

Метод итераций Итерационная последовательность {xn} : 1)сходится, т. е. имеет предел, равный корню уравнения f(x)=0 или 2) расходится, т. е. не имеет предела. 9

Теорема о сходимости итерационной последовательности • Пусть на отрезке [a, b] имеется единственный корень уравнения x= (x) и во всех точках этого отрезка (x) удовлетворяет неравенству: (x) q<1. Если при этом выполняется и условие a (x) b, то итерационный процесс сходится и за нулевое приближение x 0 можно взять любое число из отрезка [a, b]. 10

Теорема о сходимости итерационной последовательности • Чем меньше - угловой коэффициент касательной, тем лучше сходимость итерационного процесса. 11

Критерий окончания итерационного процесса: Если поставить условие, что истинное значение корня должно отличаться от приближенного значения на величину , т. е. , то приближения надо вычислять до тех пор пока будет выполнено неравенство: или , где q определяется из соотношения: 12

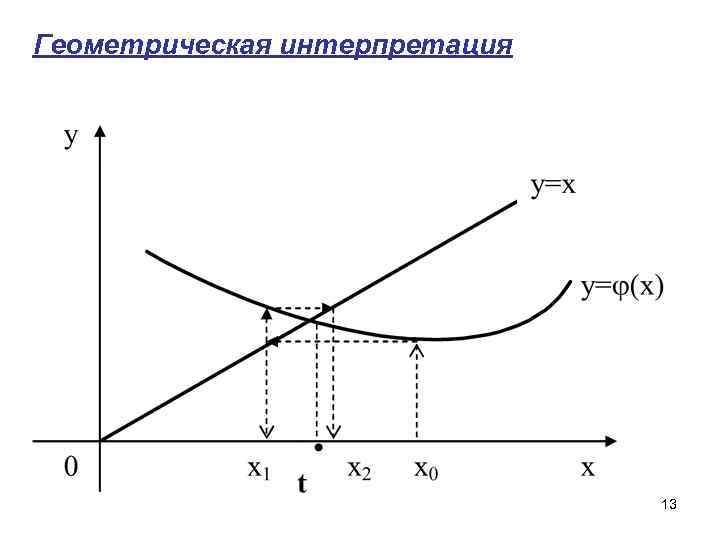Геометрическая интерпретация 13

Пример3: Найти приближенное значение корня на отрезке [0, 1] методом итераций 14

Решение: • На отрезке [0, 1] т. е. выполняется условие где q=0, 85. Принимаем за (середина отр. ) Тогда , , и т. д. 15

продолжение решения: • Нечетные результаты с избытком, четные – с недостатком. …………… 16

продолжение решения: • Точность, достигнутая после 19 итераций, примерно соответствует точности 12 шагов метода бисекции. • Метод Ньютона: после четвертого шага процесс останавливается (пятая итерация дает тот же результат) 17

Построение графиков в Math. Cad Построить график функции y=2 sin 2 x. n Набираем на экране y(x): =2 sin (2 x). Отводим указатель мыши от выделенной части и щелкаем левой кнопкой мышки. Указатель мыши подводим к “Построение графиков”, входим и активизируем “Декартов график”. 18

Построение графиков в Math. Cad n Появляется шаблон для построения графика. На нём выделены метки. Указатель мыши подводим к нижней метке, активизируем. Набираем x. n Появляются по горизонтали еще две метки, где мы должны указать интервалы построения графика. 19

Построение графиков в Math. Cad Указатель мыши подводим к левой метке, щелкая левой кнопкой мыши, активизируем и вводим левую границу 0. Указатель мыши подводим к правой границе, активизируем и вводим 5. Уводим указатель мыши к метке оси Y, активизируем его и вводим y(x). 20

Построение графиков в Math. Cad Появляются метки нижней и верхней границ оси Y. В нижней набираем – 2, в верхней 2. Отводим указатель мыши от шаблона для графиков, щелкаем левой кнопкой мыши. Появляется искомый график. 21

Построение графиков в Math. Cad Для форматирования графика нужно дважды щелкнуть в области графика. В выпавшем меню можно управлять отображением линий, масштабом и др. 22

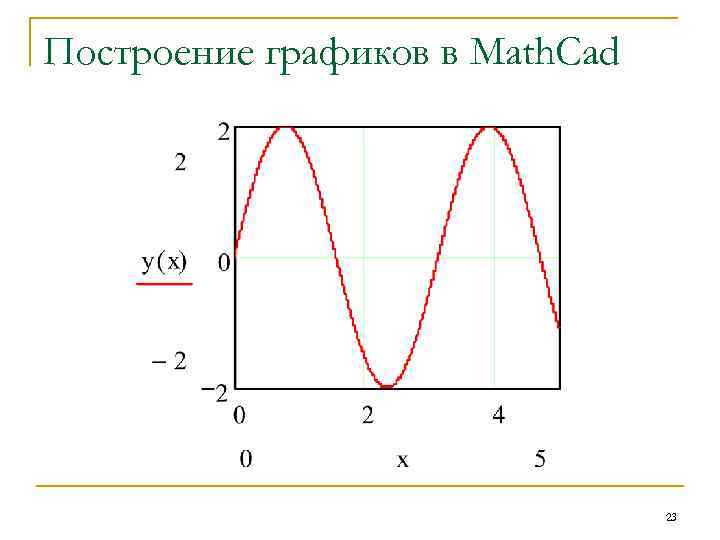Построение графиков в Math. Cad 23