ЧМ Л3 - мет хорд, Ньютона 09_11г.ppt
- Количество слайдов: 35
 ЧИСЛЕННЫЕ МЕТОДЫ Лекция 3: Методы решения нелинейных уравнений
ЧИСЛЕННЫЕ МЕТОДЫ Лекция 3: Методы решения нелинейных уравнений
 Метод хорд (линейное интерполирование). Пусть дано уравнение f(x)=0, где f(x) непрерывная функция, имеющая в интервале (a, b) производные первого и второго порядка. Корень отделен и находится на отрезке [a, b], т. е. f(a) f(b)<0. Ø Идея метода заключается в том, что на достаточно малом промежутке [a, b] дуга кривой y=f(x) заменяется стягивающей ее хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью Оx. Ø
Метод хорд (линейное интерполирование). Пусть дано уравнение f(x)=0, где f(x) непрерывная функция, имеющая в интервале (a, b) производные первого и второго порядка. Корень отделен и находится на отрезке [a, b], т. е. f(a) f(b)<0. Ø Идея метода заключается в том, что на достаточно малом промежутке [a, b] дуга кривой y=f(x) заменяется стягивающей ее хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью Оx. Ø
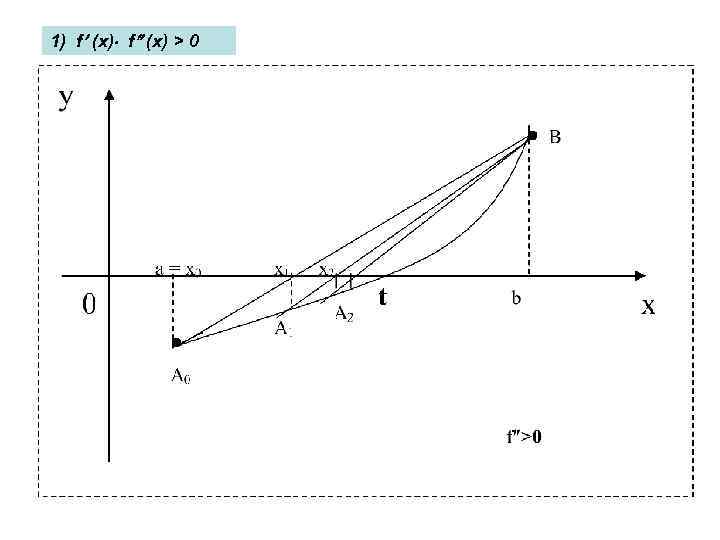 1) f (x) > 0
1) f (x) > 0
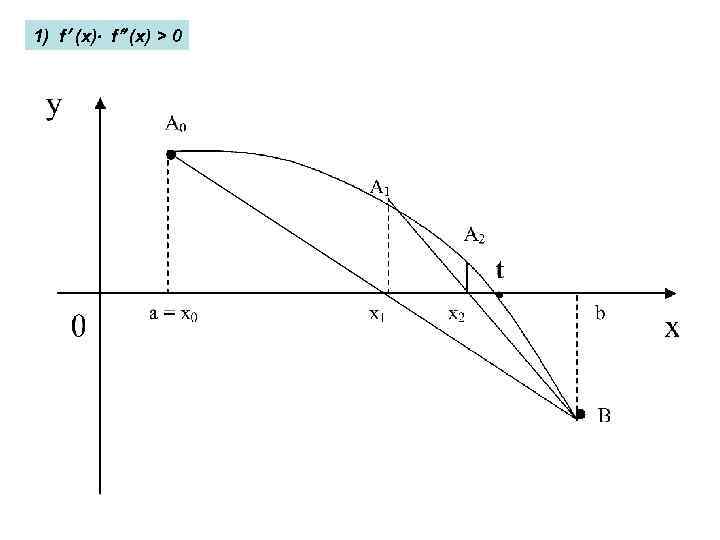 1) f (x) > 0
1) f (x) > 0
 Вывод формулы метода хорд • Уравнение хорды A 0 B: из уравнения прямой, проходящей через две точки: • Найдем значение x=x 1 для которого y=0. или Это формула метода хорд для первого шага. (1)
Вывод формулы метода хорд • Уравнение хорды A 0 B: из уравнения прямой, проходящей через две точки: • Найдем значение x=x 1 для которого y=0. или Это формула метода хорд для первого шага. (1)
![Вывод формулы метода хорд • Сейчас корень внутри отрезка [x 1, b]. • Далее: Вывод формулы метода хорд • Сейчас корень внутри отрезка [x 1, b]. • Далее:](https://present5.com/presentation/6261624_26560505/image-6.jpg) Вывод формулы метода хорд • Сейчас корень внутри отрезка [x 1, b]. • Далее: (2) • Здесь В – неподвижный конец хорды.
Вывод формулы метода хорд • Сейчас корень внутри отрезка [x 1, b]. • Далее: (2) • Здесь В – неподвижный конец хорды.
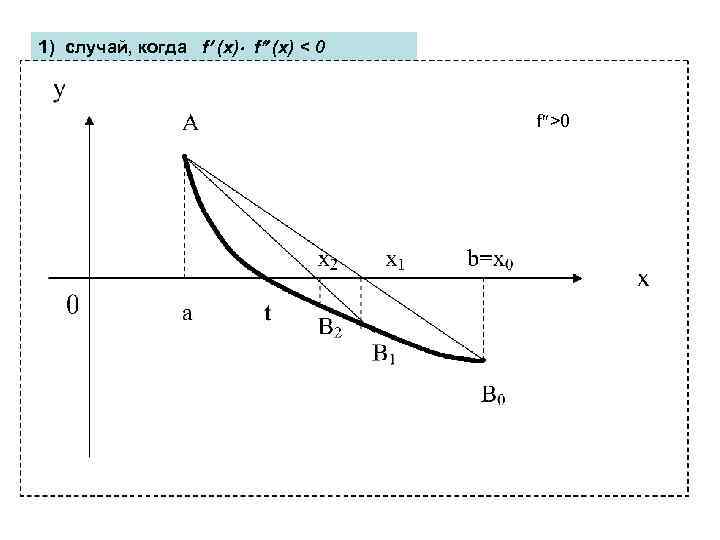 1) случай, когда f (x) < 0 f >0
1) случай, когда f (x) < 0 f >0
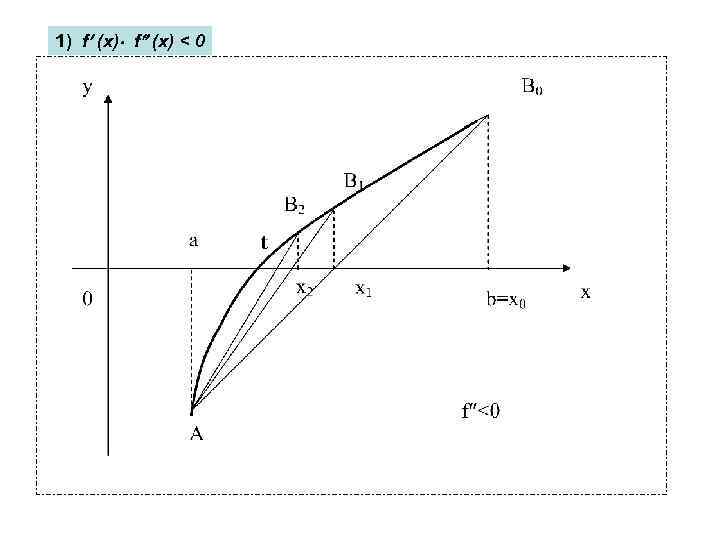 1) f (x) < 0
1) f (x) < 0
 Вывод формулы метода хорд • Уравнение хорды AB 0: • Найдем точку x 1 при y=0. (3) • Итак до (n+1)-го шага: (4) • Здесь А-неподвижный конец хорды.
Вывод формулы метода хорд • Уравнение хорды AB 0: • Найдем точку x 1 при y=0. (3) • Итак до (n+1)-го шага: (4) • Здесь А-неподвижный конец хорды.
 Правило выбора формул: o неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной. o Оценка погрешности метода:
Правило выбора формул: o неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной. o Оценка погрешности метода:
 Пример: Методом хорд уточнить до =0, 001 меньший корень уравнения: Корни отделены и меньший содержится на отрезке
Пример: Методом хорд уточнить до =0, 001 меньший корень уравнения: Корни отделены и меньший содержится на отрезке
 Решение: • Процесс приближения к корню следует продолжать до тех пор, пока не будет выполнено условие:
Решение: • Процесс приближения к корню следует продолжать до тех пор, пока не будет выполнено условие:
 продолжение решения: • Определим знак второй производной: • Значит, за неподвижный конец отрезка нужно принять • Тогда вычисления ведём по формулам (3), (4), где и
продолжение решения: • Определим знак второй производной: • Значит, за неподвижный конец отрезка нужно принять • Тогда вычисления ведём по формулам (3), (4), где и
 продолжение решения: • Если записать (4) в виде: , то сразу же можно будет получить разность между последними приближениями и проверять выполнение неравенства
продолжение решения: • Если записать (4) в виде: , то сразу же можно будет получить разность между последними приближениями и проверять выполнение неравенства
 продолжение решения: • Условие выполнено. • Ответ:
продолжение решения: • Условие выполнено. • Ответ:
![Метод Ньютона (метод касательных). Пусть корень уравнения f(x)=0 отделен на отрезке [a, b], причем Метод Ньютона (метод касательных). Пусть корень уравнения f(x)=0 отделен на отрезке [a, b], причем](https://present5.com/presentation/6261624_26560505/image-16.jpg) Метод Ньютона (метод касательных). Пусть корень уравнения f(x)=0 отделен на отрезке [a, b], причем f (x) и f (x) непрерывны и сохраняют постоянные знаки на отрезке [a, b]. Геометрический смысл метода Ньютона состоит в том, что дуга кривой y=f(x) заменяется касательной к этой кривой.
Метод Ньютона (метод касательных). Пусть корень уравнения f(x)=0 отделен на отрезке [a, b], причем f (x) и f (x) непрерывны и сохраняют постоянные знаки на отрезке [a, b]. Геометрический смысл метода Ньютона состоит в том, что дуга кривой y=f(x) заменяется касательной к этой кривой.
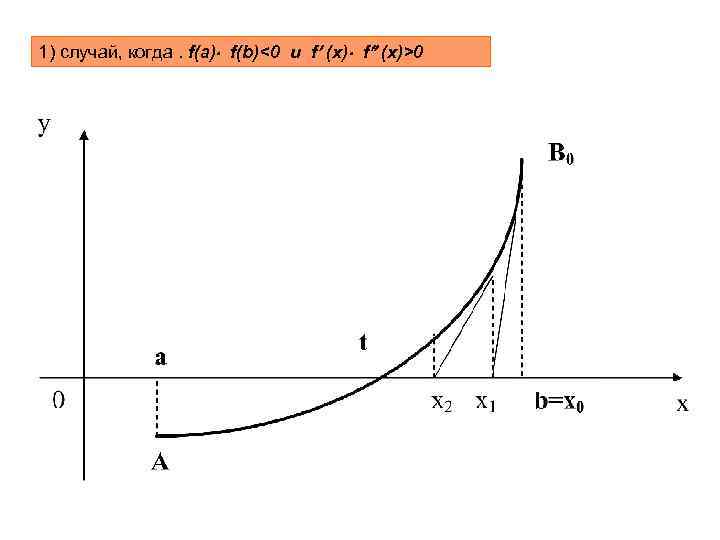 1) случай, когда. f(a) f(b)<0 и f (x)>0
1) случай, когда. f(a) f(b)<0 и f (x)>0
 Уравнение касательной в точке B 0: полагая y=0, x=x 1 получим: продолжая этот процесс, получаем последовательность {xn}, определённую с помощью рекуррентной формулы: (1)
Уравнение касательной в точке B 0: полагая y=0, x=x 1 получим: продолжая этот процесс, получаем последовательность {xn}, определённую с помощью рекуррентной формулы: (1)
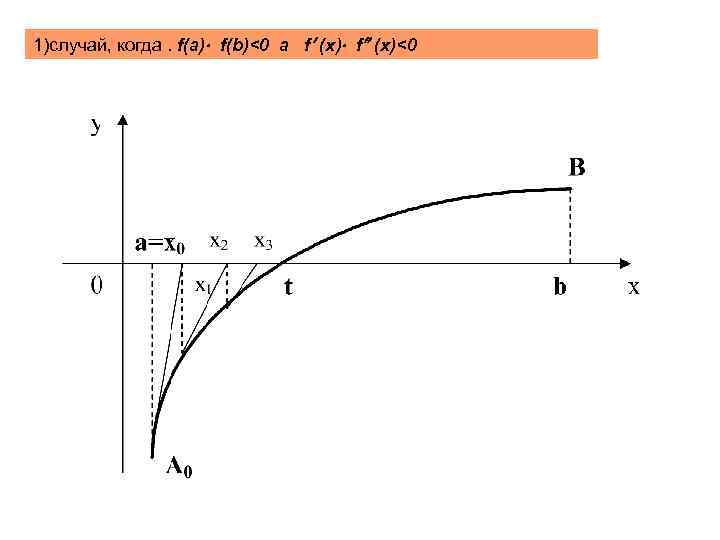 1)случай, когда. f(a) f(b)<0 а f (x)<0
1)случай, когда. f(a) f(b)<0 а f (x)<0
 Уравнение касательной в точке A 0: , при y=0, x=x 1 , И наконец, формула метода Ньютона:
Уравнение касательной в точке A 0: , при y=0, x=x 1 , И наконец, формула метода Ньютона:
![Теорема о сходимости метода Ньютона: Пусть x=t - принадлежит отрезку [a, b] и является Теорема о сходимости метода Ньютона: Пусть x=t - принадлежит отрезку [a, b] и является](https://present5.com/presentation/6261624_26560505/image-21.jpg) Теорема о сходимости метода Ньютона: Пусть x=t - принадлежит отрезку [a, b] и является корнем уравнения f(x)=0, а функция f(x) дважды непрерывно дифференцируема на данном отрезке. Тогда найдется такая -окрестность точки x=t, что при любом выборе начального приближения x 0 на отрезке [t- , t+ ] [a, b]
Теорема о сходимости метода Ньютона: Пусть x=t - принадлежит отрезку [a, b] и является корнем уравнения f(x)=0, а функция f(x) дважды непрерывно дифференцируема на данном отрезке. Тогда найдется такая -окрестность точки x=t, что при любом выборе начального приближения x 0 на отрезке [t- , t+ ] [a, b]
 Теорема о сходимости метода Ньютона: существует бесконечная итерационная последовательность (1) и эта последовательность сходится к корню t. Достаточное условие сходимости метода Ньютона: f(x) f (x) <[ f (x)]2.
Теорема о сходимости метода Ньютона: существует бесконечная итерационная последовательность (1) и эта последовательность сходится к корню t. Достаточное условие сходимости метода Ньютона: f(x) f (x) <[ f (x)]2.
 Правило выбора начального приближения: • за исходную точку (нулевое приближение) следует выбирать тот конец отрезка [a, b], в котором знак функции совпадает со знаком второй производной.
Правило выбора начального приближения: • за исходную точку (нулевое приближение) следует выбирать тот конец отрезка [a, b], в котором знак функции совпадает со знаком второй производной.
 Критерий окончания итерационного процесса: при заданной точности >0 вычисления следует вести до тех пор, пока не окажется выполненным неравенство: xn – xn-1 <. Оценка погрешности метода: где
Критерий окончания итерационного процесса: при заданной точности >0 вычисления следует вести до тех пор, пока не окажется выполненным неравенство: xn – xn-1 <. Оценка погрешности метода: где
 ПРИМЕР 1: • Найти методом касательных приближенное значение корня уравнения f(x) = x - cosx = 0 на интервале [0, 5; 1].
ПРИМЕР 1: • Найти методом касательных приближенное значение корня уравнения f(x) = x - cosx = 0 на интервале [0, 5; 1].
 Решение: • Рекуррентная формула метода касательных принимает в данном случае вид:
Решение: • Рекуррентная формула метода касательных принимает в данном случае вид:
 продолжение решения: • Выберем в качестве нулевого приближения x 0=0, 5 и подсчитаем следующие приближения. Результаты вычислений приведены в таблице: После двух шагов мы достигли точности 10 -4.
продолжение решения: • Выберем в качестве нулевого приближения x 0=0, 5 и подсчитаем следующие приближения. Результаты вычислений приведены в таблице: После двух шагов мы достигли точности 10 -4.
 ПРИМЕР 2: Рассмотрим вычисление как задачу решения уравнения: x 2 - a = 0 в области x>0. Написать для вычисления корня уравнения итерационную последова-тельность по методу касательных. Вычислить с её помощью.
ПРИМЕР 2: Рассмотрим вычисление как задачу решения уравнения: x 2 - a = 0 в области x>0. Написать для вычисления корня уравнения итерационную последова-тельность по методу касательных. Вычислить с её помощью.
 Решение: Рекуррентная формула метода касательных для уравнения принимает вид: (* )
Решение: Рекуррентная формула метода касательных для уравнения принимает вид: (* )
 продолжение решения: Перейдём к вычислению. Вспомним, что. Выбирая x 0=2, делаем несколько итераций по формуле (*): x 0=2; x 1=1, 5;
продолжение решения: Перейдём к вычислению. Вспомним, что. Выбирая x 0=2, делаем несколько итераций по формуле (*): x 0=2; x 1=1, 5;
 продолжение решения: Третий шаг определяет ностью: с погреш-
продолжение решения: Третий шаг определяет ностью: с погреш-
 Лабораторная работа: Метод бисекции. Текст программы:
Лабораторная работа: Метод бисекции. Текст программы:
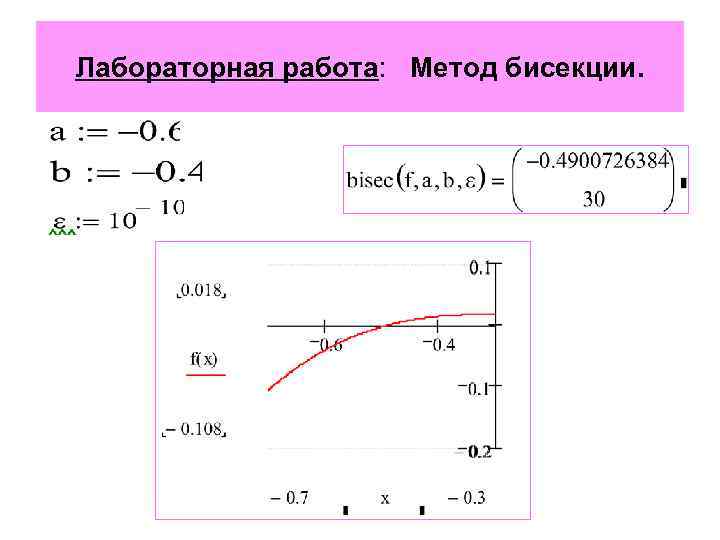 Лабораторная работа: Метод бисекции.
Лабораторная работа: Метод бисекции.
 Метод Ньютона:
Метод Ньютона:
 Метод Ньютона:
Метод Ньютона:
