Численные методы Ч 2 Численное интегрирование Численное

Численные методы Ч 2. Численное интегрирование

Численное интегрирование Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). f(x)

Такой функцией обычно является полином (кусочный полином) – априорная погрешность метода на интервале интегрирования r(x) априорная погрешность метода на отдельном шаге интегрирования

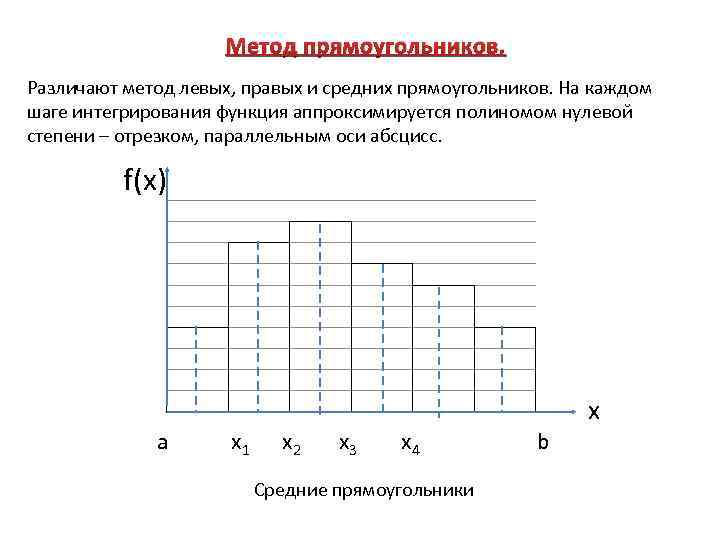Метод прямоугольников. Различают метод левых, правых и средних прямоугольников. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс. f(x) a x 1 x 2 x 3 x 4 Средние прямоугольники b x

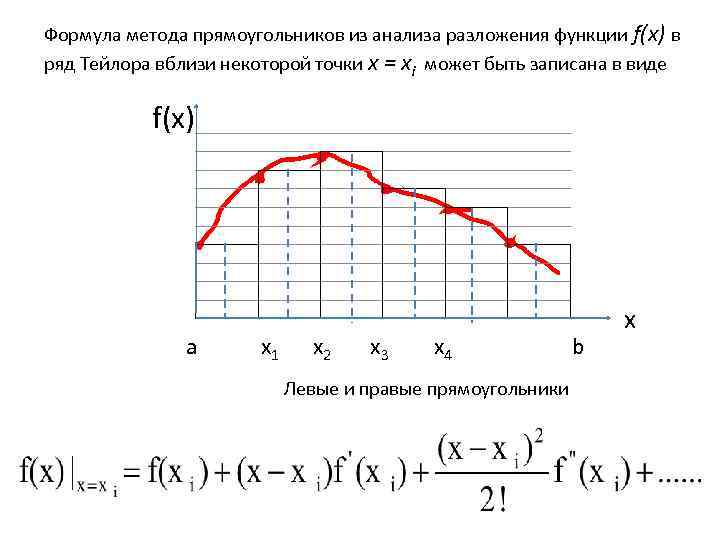Формула метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = xi может быть записана в виде f(x) a x 1 x 2 x 3 x 4 Левые и правые прямоугольники b x

Рассмотрим диапазон интегрирования от xi до xi+h, где h – шаг интегрирования Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности

В случае равного шага формула имеет вид h на всем диапазоне интегрирования общая h=const

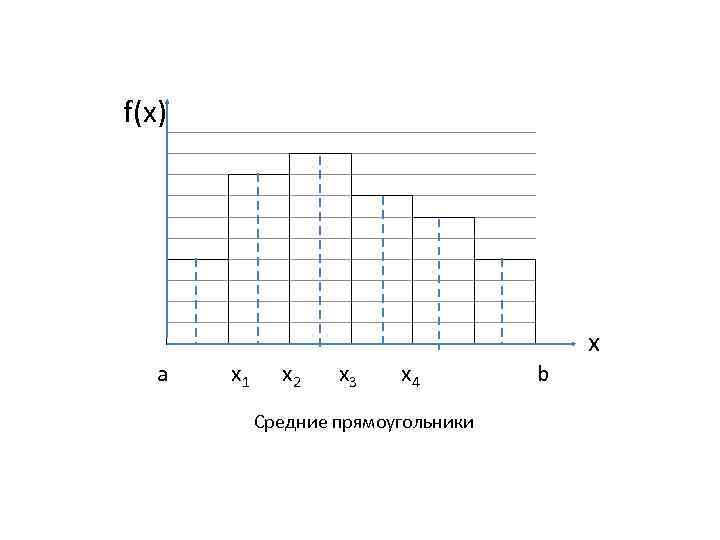f(x) a x 1 x 2 x 3 x 4 Средние прямоугольники b x

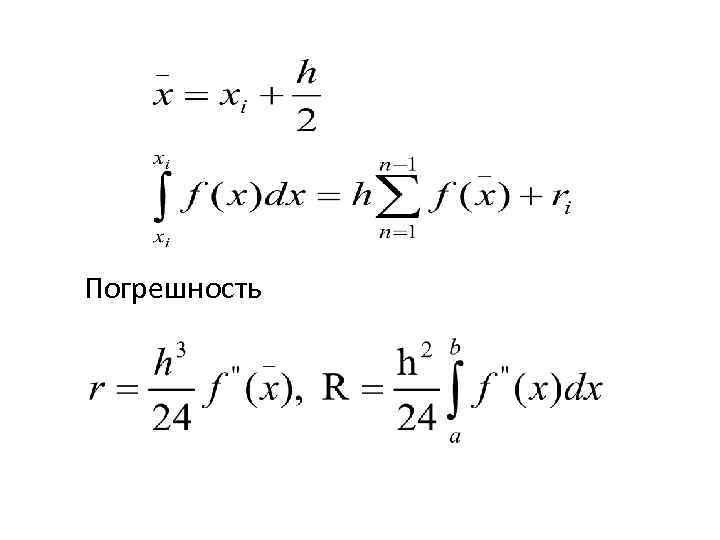Погрешность

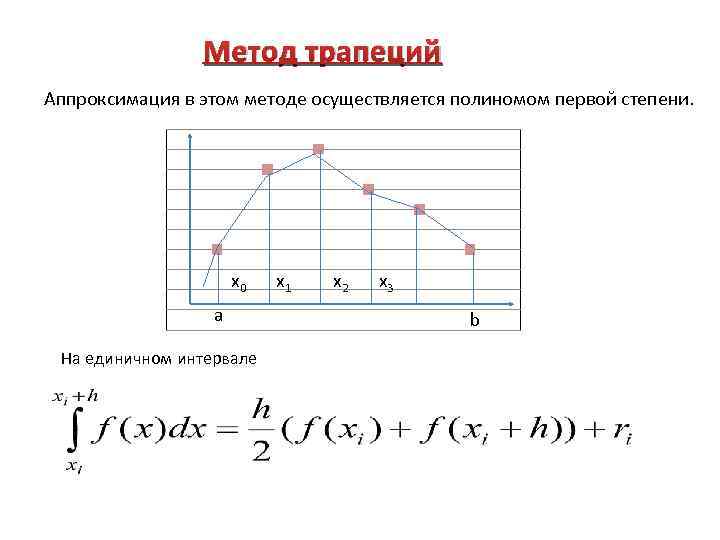Метод трапеций Аппроксимация в этом методе осуществляется полиномом первой степени. x 0 a На единичном интервале x 1 x 2 x 3 b

Равномерная сетка h=const

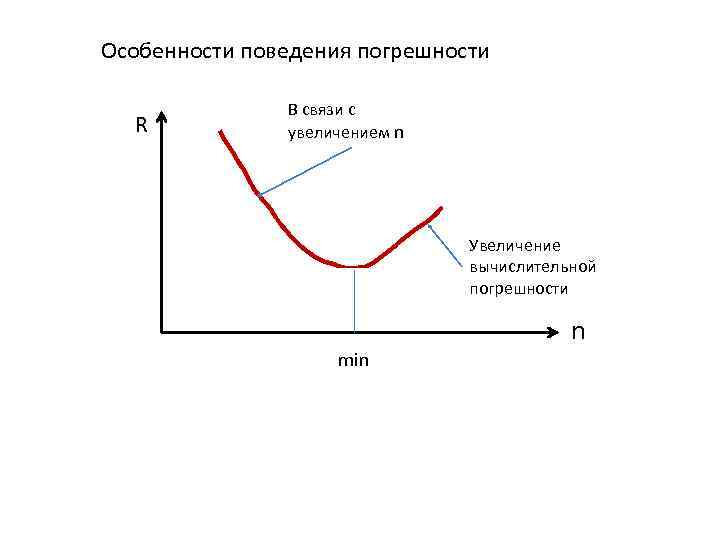Особенности поведения погрешности R В связи с увеличением n Увеличение вычислительной погрешности min n

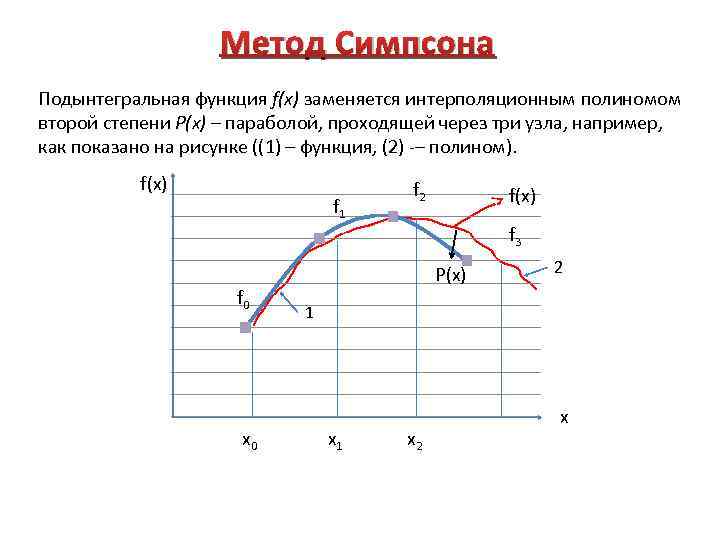Метод Симпсона Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином). f(x) f 1 f 2 f(x) f 3 f 0 x 0 P(x) 2 1 x 2 x

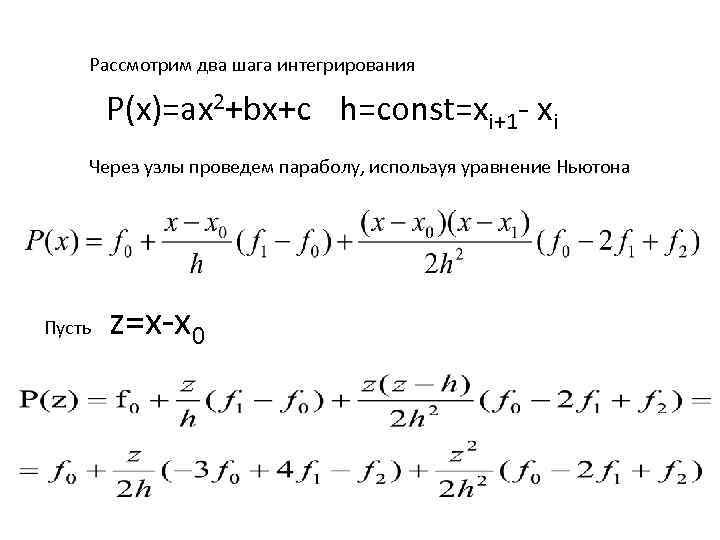Рассмотрим два шага интегрирования P(x)=ax 2+bx+c h=const=xi+1 xi Через узлы проведем параболу, используя уравнение Ньютона Пусть z=x x 0

Теперь, воспользовавшись полученным соотношением, сосчитаем интеграл по данному интервалу:

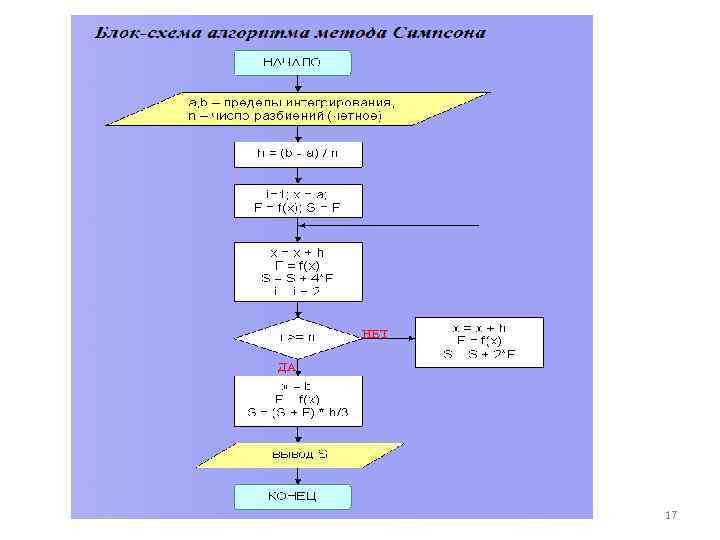
Для равномерной сетки и четного числа шагов принимает вид: n формула Симпсона

17

18