Численные методы анализа.






















chisl_met_an_ch.3_i_4[1].pptx
- Размер: 893.6 Кб
- Автор:
- Количество слайдов: 27
Описание презентации Численные методы анализа. по слайдам
 Численные методы анализа. ч. 3 -4. «Всё опыт, опыт! Опыт – это вздор. Значенья духа опыт не покроет. Всё, что узнали до сих пор, искать не стоило. И знать не стоит. » Монолог Бакалавра. «Фауст» , Гёте
Численные методы анализа. ч. 3 -4. «Всё опыт, опыт! Опыт – это вздор. Значенья духа опыт не покроет. Всё, что узнали до сих пор, искать не стоило. И знать не стоит. » Монолог Бакалавра. «Фауст» , Гёте
 3. Численные методы решения систем уравнений 3. 1. Основные положения 1. Точные методы – конечные алгоритмы для вычисления корней системы. 2. Итерационные методы – решение системы путем сходящихся итерационных процессов. Источники погрешностей: округления (даже в точных методах) и погрешности метода.
3. Численные методы решения систем уравнений 3. 1. Основные положения 1. Точные методы – конечные алгоритмы для вычисления корней системы. 2. Итерационные методы – решение системы путем сходящихся итерационных процессов. Источники погрешностей: округления (даже в точных методах) и погрешности метода.
 33. 2. Метод Крамера (решение систем линейных уравнений с помощью обратной матрицы) Неособенная матрица А : Обратная матрица А -1 : Присоединенная матрица Ã – транспонированная матрица, составленная из миноров A ij со своими знаками. , , , nnnnnn nn nn bxaxaxa. . . . 2211 22222121 11212111 bx. A 0 det. A b. Ax 1 nnnn n n AAA AAA. . . . 1~1 21 22212 12111 1 AA nn nn bbb xxx aaa aaa. . . . .
33. 2. Метод Крамера (решение систем линейных уравнений с помощью обратной матрицы) Неособенная матрица А : Обратная матрица А -1 : Присоединенная матрица Ã – транспонированная матрица, составленная из миноров A ij со своими знаками. , , , nnnnnn nn nn bxaxaxa. . . . 2211 22222121 11212111 bx. A 0 det. A b. Ax 1 nnnn n n AAA AAA. . . . 1~1 21 22212 12111 1 AA nn nn bbb xxx aaa aaa. . . . .
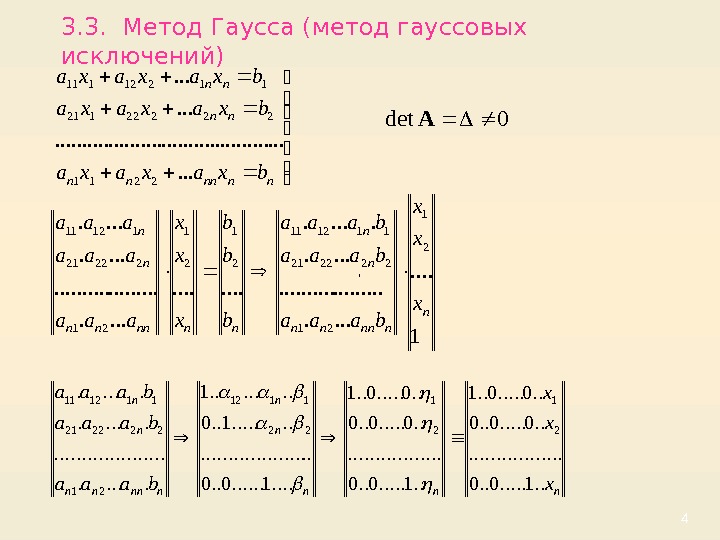
 43. 3. Метод Гаусса (метод гауссовых исключений) , nnnnnn nn nn bxaxaxa. . . . 2211 22222121 11212111 0 det. A nnn n n nnnnn n n x x x baaa. . 1. . 0. . . 0. . 0. . 1. . . 0. . . . 1. . . . . 2 1 22 1112 21 222221 111211 1. . . . . 21 21 222221 111211 21 22221 11211 n nnnnn nn x x x baaa b b b x x x aaa aaa
43. 3. Метод Гаусса (метод гауссовых исключений) , nnnnnn nn nn bxaxaxa. . . . 2211 22222121 11212111 0 det. A nnn n n nnnnn n n x x x baaa. . 1. . 0. . . 0. . 0. . 1. . . 0. . . . 1. . . . . 2 1 22 1112 21 222221 111211 1. . . . . 21 21 222221 111211 21 22221 11211 n nnnnn nn x x x baaa b b b x x x aaa aaa
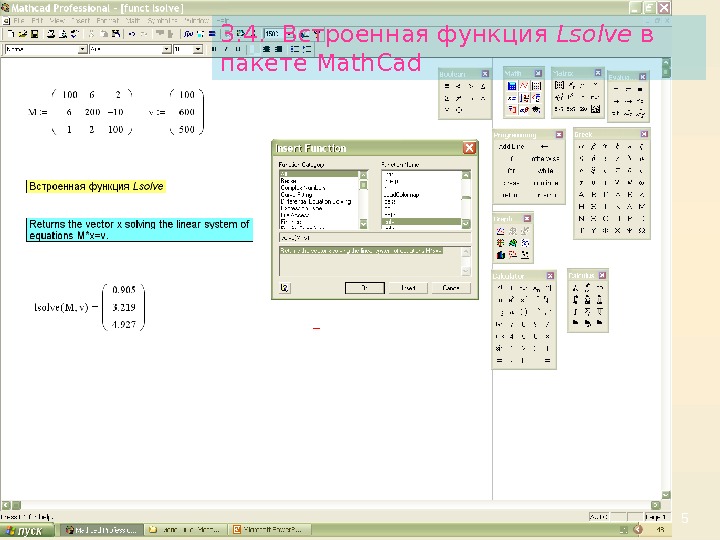
 53. 4. Встроенная функция Lsolve в пакете Math. Cad
53. 4. Встроенная функция Lsolve в пакете Math. Cad
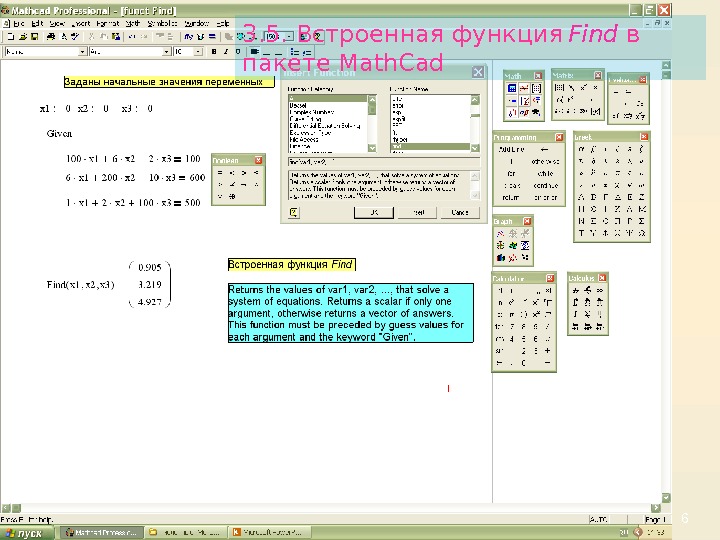
 63. 5. Встроенная функция Find в пакете Math. Cad
63. 5. Встроенная функция Find в пакете Math. Cad
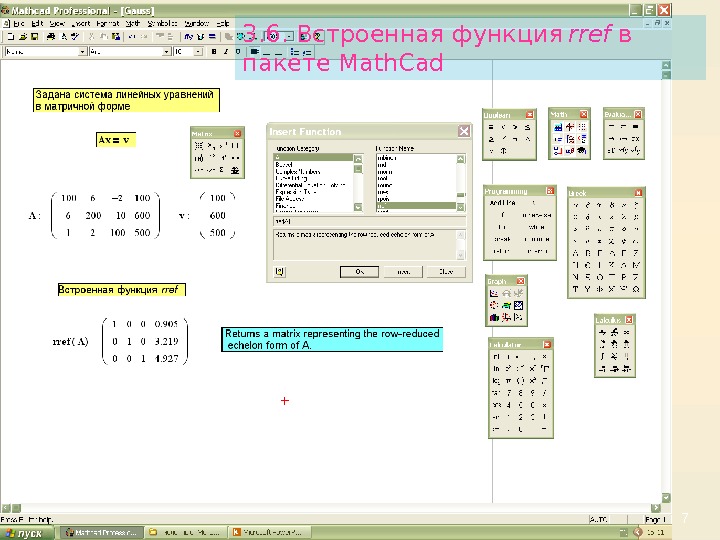
 73. 6. Встроенная функция rref в пакете Math. Cad
73. 6. Встроенная функция rref в пакете Math. Cad
 83. 7. Метод итераций Дана система n линейных уравнений Предполагается, что диагональные коэффициенты отличны от нуля Система приводится к виду или в матричном виде Нулевое приближение k -ое приближение 1)1(2211 22312122 122211. . . . nnnnnnn nn nn xxxx xxx n j ijijbxa 1 0 iia xαβx βx )0( )1()( kk xαβx
83. 7. Метод итераций Дана система n линейных уравнений Предполагается, что диагональные коэффициенты отличны от нуля Система приводится к виду или в матричном виде Нулевое приближение k -ое приближение 1)1(2211 22312122 122211. . . . nnnnnnn nn nn xxxx xxx n j ijijbxa 1 0 iia xαβx βx )0( )1()( kk xαβx
 9 Теорема сходимости итерационного ряда Теорема. Процесс итерации для линейной системы уравнений сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы α меньше единицы, т. е. достаточным условием сходимости является неравенство ║ α ║< 1. Следствие 1. Процесс итерации сходится, если: 1. Неопределенная норма или m -норма: 2. L 1 норма или l- норма: 3. Евклидова норма или k -норма: xαβx n j ij m i 1 1 max n i ij l j 1 1 max 1, 2 n ji ijki
9 Теорема сходимости итерационного ряда Теорема. Процесс итерации для линейной системы уравнений сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы α меньше единицы, т. е. достаточным условием сходимости является неравенство ║ α ║< 1. Следствие 1. Процесс итерации сходится, если: 1. Неопределенная норма или m -норма: 2. L 1 норма или l- норма: 3. Евклидова норма или k -норма: xαβx n j ij m i 1 1 max n i ij l j 1 1 max 1, 2 n ji ijki
 10 Следствие 2. Процесс итерации сходится, если выполнены неравенства : 1. 2. Условия окончания итерационного процесса: n j ijiiaa 1 ‘ n j ijjjaa 1’ )1( )()1( k kk x xx
10 Следствие 2. Процесс итерации сходится, если выполнены неравенства : 1. 2. Условия окончания итерационного процесса: n j ijiiaa 1 ‘ n j ijjjaa 1’ )1( )()1( k kk x xx
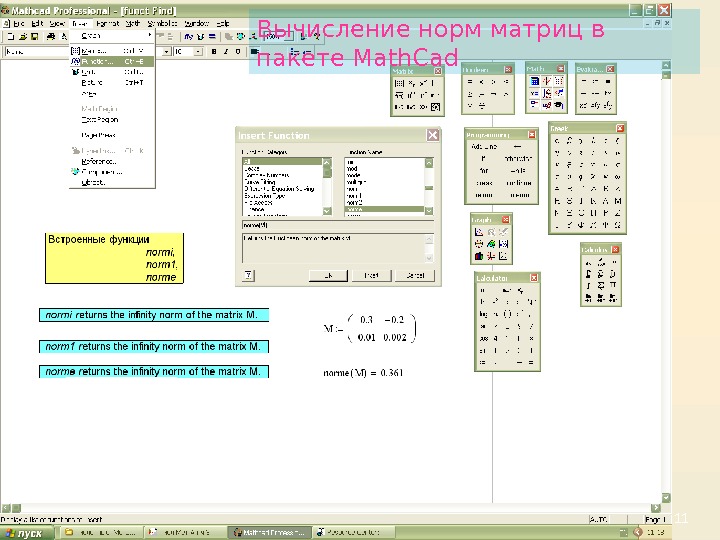
 11 Вычисление норм матриц в пакете Math. Cad
11 Вычисление норм матриц в пакете Math. Cad
 123. 8. Метод Зейделя (модификация метода итераций) При вычислении ( k+1 ) приближения неизвестной x i учитываются уже вычисленные ранее ( k+1) приближения неизвестных x 1 , x 2 , … x i-1. Система приводится к виду ( k +1) -ое приближение Нулевое приближение В матричном виде 1)1(2211 22312122 122211. . . . nnnnnnn xxxx xxx 1 1 )1()1( 1 )( 1 1 )1()1( 3 )1( 1212 )1( 2 2 )( 11 )1( 1 n j k jnjn k n n mj k jmj m j k jmjm k m n j k jj kk n j k jj k xaxax xax xαβx βx )0(
123. 8. Метод Зейделя (модификация метода итераций) При вычислении ( k+1 ) приближения неизвестной x i учитываются уже вычисленные ранее ( k+1) приближения неизвестных x 1 , x 2 , … x i-1. Система приводится к виду ( k +1) -ое приближение Нулевое приближение В матричном виде 1)1(2211 22312122 122211. . . . nnnnnnn xxxx xxx 1 1 )1()1( 1 )( 1 1 )1()1( 3 )1( 1212 )1( 2 2 )( 11 )1( 1 n j k jnjn k n n mj k jmj m j k jmjm k m n j k jj kk n j k jj k xaxax xax xαβx βx )0(
 133. 9. Метода итераций для систем нелинейных уравнений Задана система уравнений и начальные приближения корней x (0) 0 , x (0) 2 , …x (0) n : Система приводится к виду ( k +1) -ое приближение 1 -ое приближение 0), . . . , (. . . . 0), . . . , (21 212 211 nn n n xxx. F ), . . . , (. . . . ), . . . , ( 21 2122 2111 nnn nn xxxx ), . . . , (. . . . . ), . . . , ( )0()0( 2 )0( 1 )1( )0()0( 2 )0( 12 )1( 2 )0()0( 2 )0( 11 )1( 1 nnn n n xxxx ), . . . , (. . . . . ), . . . , ( )()( 2 )( 1 )1( )()( 2 )( 12 )1( 2 )()( 2 )( 11 )1( 1 k n k n kkk xxxx
133. 9. Метода итераций для систем нелинейных уравнений Задана система уравнений и начальные приближения корней x (0) 0 , x (0) 2 , …x (0) n : Система приводится к виду ( k +1) -ое приближение 1 -ое приближение 0), . . . , (. . . . 0), . . . , (21 212 211 nn n n xxx. F ), . . . , (. . . . ), . . . , ( 21 2122 2111 nnn nn xxxx ), . . . , (. . . . . ), . . . , ( )0()0( 2 )0( 1 )1( )0()0( 2 )0( 12 )1( 2 )0()0( 2 )0( 11 )1( 1 nnn n n xxxx ), . . . , (. . . . . ), . . . , ( )()( 2 )( 1 )1( )()( 2 )( 12 )1( 2 )()( 2 )( 11 )1( 1 k n k n kkk xxxx
 144. Интерполирование функций 4. 1. Интерполяционная формула Лагранжа Постановка задачи. 1. На отрезке [ a, b ] заданы n +1 значения аргумента x : x 0 , x 1 , …. x n (узлы) и значения функции y i =f ( x i ). Требуется построить полином L n ( x ) степени не выше n , имеющий в заданных узлах те же значения, что и функция f ( x ) , т. е. L n ( x i ) = y i при ( i=0, 1, 2, …n ). 2. Шаг интерполяции h i+1 =( x i+1 -x i ) может быть произвольным (узлы не являются равноотстоящими. ) Представим полином в виде В результате получим систему n +1 уравнений с n +1 неизвестными a 0 , a 1 , a 2 , …a n : n nnxaxaax. L. . . )(10 nnnnn n n yxaxaxaa. . . .
144. Интерполирование функций 4. 1. Интерполяционная формула Лагранжа Постановка задачи. 1. На отрезке [ a, b ] заданы n +1 значения аргумента x : x 0 , x 1 , …. x n (узлы) и значения функции y i =f ( x i ). Требуется построить полином L n ( x ) степени не выше n , имеющий в заданных узлах те же значения, что и функция f ( x ) , т. е. L n ( x i ) = y i при ( i=0, 1, 2, …n ). 2. Шаг интерполяции h i+1 =( x i+1 -x i ) может быть произвольным (узлы не являются равноотстоящими. ) Представим полином в виде В результате получим систему n +1 уравнений с n +1 неизвестными a 0 , a 1 , a 2 , …a n : n nnxaxaax. L. . . )(10 nnnnn n n yxaxaxaa. . . .
 15 Неизвестные a i можно найти методом Крамера Функция Q i ( x ) должна удовлетворять условиям Её явный вид. Тогда полином примет вид Интерполяционная формула Лагранжа n na )). . . ()(). . . ()(( )( 1110 niiiiiii nii ixxxxxxxxxx x. Q ijji x. Q )( )(. . . )()()(1100 x. Qyx. Lnnn n iniiiiiii nn xxxxxxxxxx yx. L 01110 )). . . ()(). . . ()(( )(
15 Неизвестные a i можно найти методом Крамера Функция Q i ( x ) должна удовлетворять условиям Её явный вид. Тогда полином примет вид Интерполяционная формула Лагранжа n na )). . . ()(). . . ()(( )( 1110 niiiiiii nii ixxxxxxxxxx x. Q ijji x. Q )( )(. . . )()()(1100 x. Qyx. Lnnn n iniiiiiii nn xxxxxxxxxx yx. L 01110 )). . . ()(). . . ()(( )(
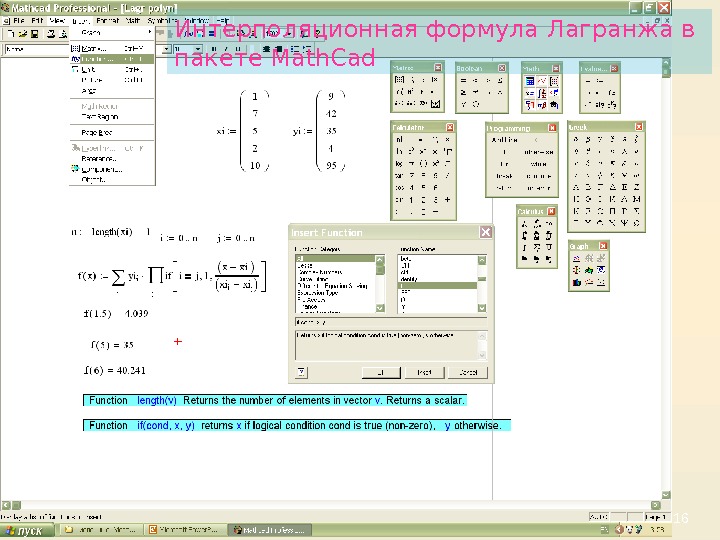
 16 Интерполяционная формула Лагранжа в пакете Math. Cad
16 Интерполяционная формула Лагранжа в пакете Math. Cad
 174. 2. Интерполяционные формулы Ньютона Определения. 1. Конечные разности первого порядка: Δ y i = y i+1 – y i 2. Конечные разности второго порядка: Δ 2 y i = Δ y i+1 – Δ y i = y i+2 – 2 y i+1 + y i 3. Конечные разности n -ого порядка : Δ n y i = Δ n-1 y i+1 – Δ n-1 y i. Рассматриваемые значения аргумента являются равноотстоящими, т. е. образуют арифметическую прогрессию (шаг интерполяции h = const) .
174. 2. Интерполяционные формулы Ньютона Определения. 1. Конечные разности первого порядка: Δ y i = y i+1 – y i 2. Конечные разности второго порядка: Δ 2 y i = Δ y i+1 – Δ y i = y i+2 – 2 y i+1 + y i 3. Конечные разности n -ого порядка : Δ n y i = Δ n-1 y i+1 – Δ n-1 y i. Рассматриваемые значения аргумента являются равноотстоящими, т. е. образуют арифметическую прогрессию (шаг интерполяции h = const) .
 18 Пусть для функции, заданной таблично с постоянным шагом, составлена таблица конечных разностей. Будем искать интерполяционный полином в виде 4. 2. 1. Первая интерполяционная формула Ньютона Коэффициенты a 0 , a 1 , …. a n найдем из условия совпадения значений функции и интерполяционного полинома в узлах интерполяции. Полагая x = x 0 , находим y 0 = P n ( x 0 )= a 0. Далее подставляя x = x 1 , находим y 1 = P n ( x 1 )= a 0 + a 1 ( x 1 — x 0 )= a 0 + a 1 h, x = x 2 , находим y 2 = P n ( x 2 )= a 0 + a 1 ( x 1 — x 0 )+ a 2 ( x 2 — x 0 ) ( x 2 — x 1 ) = a 0 +2 a 1 h +2 a 2 h 2 , )). . . ()((). . . )(()()(110102010 nnnxxxxxxaxxaax. P
18 Пусть для функции, заданной таблично с постоянным шагом, составлена таблица конечных разностей. Будем искать интерполяционный полином в виде 4. 2. 1. Первая интерполяционная формула Ньютона Коэффициенты a 0 , a 1 , …. a n найдем из условия совпадения значений функции и интерполяционного полинома в узлах интерполяции. Полагая x = x 0 , находим y 0 = P n ( x 0 )= a 0. Далее подставляя x = x 1 , находим y 1 = P n ( x 1 )= a 0 + a 1 ( x 1 — x 0 )= a 0 + a 1 h, x = x 2 , находим y 2 = P n ( x 2 )= a 0 + a 1 ( x 1 — x 0 )+ a 2 ( x 2 — x 0 ) ( x 2 — x 1 ) = a 0 +2 a 1 h +2 a 2 h 2 , )). . . ()((). . . )(()()(110102010 nnnxxxxxxaxxaax. P
 19 Найдем коэффициенты a 1 , …. a n : Введем переменную q =( x = x 0 )/ h , ( q – число шагов). Тогда первая интерполяционная формула Ньютона примет вид: Используя понятие обобщенное степени : x [n] = x ( x-h )( x -2 h )… [ x -( n -1) h ] получим)). . . ()(( ! ). . . )(( !2 )()(1102 0 2 0 0 0 n n nxxxxxx hn y xxxx h y yx. P 2 0 !hm y a m m h y a 0 1 2 0 2 2 !2 h y a 00 2 00 ! )1). . . (1(. . . !2 )1( )(y n nqqq yqyx. Pn n nxx hn y xx h y yx. P)( !. . . )( !2 )()(
19 Найдем коэффициенты a 1 , …. a n : Введем переменную q =( x = x 0 )/ h , ( q – число шагов). Тогда первая интерполяционная формула Ньютона примет вид: Используя понятие обобщенное степени : x [n] = x ( x-h )( x -2 h )… [ x -( n -1) h ] получим)). . . ()(( ! ). . . )(( !2 )()(1102 0 2 0 0 0 n n nxxxxxx hn y xxxx h y yx. P 2 0 !hm y a m m h y a 0 1 2 0 2 2 !2 h y a 00 2 00 ! )1). . . (1(. . . !2 )1( )(y n nqqq yqyx. Pn n nxx hn y xx h y yx. P)( !. . . )( !2 )()(
 20 Для интерполирования в конце таблицы применяют вторую интерполяционную формулу Ньютона : Введем переменную q =( x — x n )/ h , тогда 4. 2. 2. Вторая интерполяционная формула Ньютона)). . . (( ! ). . . )(( !2 )( !1 )(1 0 12 2 2 1 xxxx hn y xxxx h y yx. Pnn n n n nn 022 1 ! )1). . . (1(. . . !2 )1( )(y n nqqq yqyx. P n nnnn
20 Для интерполирования в конце таблицы применяют вторую интерполяционную формулу Ньютона : Введем переменную q =( x — x n )/ h , тогда 4. 2. 2. Вторая интерполяционная формула Ньютона)). . . (( ! ). . . )(( !2 )( !1 )(1 0 12 2 2 1 xxxx hn y xxxx h y yx. Pnn n n n nn 022 1 ! )1). . . (1(. . . !2 )1( )(y n nqqq yqyx. P n nnnn
 214. 3. Кубическая сплайн-интерполяция 1. На каждом сегменте [ x i- 1 , x i ], i =1, 2, … n функция S ( x ) является полиномом третьей степени. 2. Функция S ( x ) , а также ее первая и вторая производные непрерывны на отрезке [ a, b ]. 3. S ( x i )= f ( x i ), i =0, 1, 2, … n . Кубическим интерполяционным сплайном, соответствующим данной функции f ( x ) и данным узлам x i , называется функция S ( x ) , удовлетворяющая следующим условиям На каждом из отрезков [ x i- 1 , x i ], i =1, 2, … n будем искать функцию S ( x )= S i ( x ) в виде полинома третьей степени
214. 3. Кубическая сплайн-интерполяция 1. На каждом сегменте [ x i- 1 , x i ], i =1, 2, … n функция S ( x ) является полиномом третьей степени. 2. Функция S ( x ) , а также ее первая и вторая производные непрерывны на отрезке [ a, b ]. 3. S ( x i )= f ( x i ), i =0, 1, 2, … n . Кубическим интерполяционным сплайном, соответствующим данной функции f ( x ) и данным узлам x i , называется функция S ( x ) , удовлетворяющая следующим условиям На каждом из отрезков [ x i- 1 , x i ], i =1, 2, … n будем искать функцию S ( x )= S i ( x ) в виде полинома третьей степени
 22 Коэффициенты a i , b i , c i , d i подлежат определению (т. е. нахождению) на всех n элементарных отрезках [ x i- 1 , x i ] ( i =1, 2, … n ). Для того, чтобы система алгебраических уравнений имела решение, необходимо составить 4 n уравнений Первые 2 n уравнений получаются из условия , что график пройдет через заданные точки гд е, )()(3 1 2 11 iiiixxdxxcxxbax. Siixxx 1 32 1 )( )(1 iiiii iii hdhchbax. S yax. Si 1 iiixxh ni, . . . 2,
22 Коэффициенты a i , b i , c i , d i подлежат определению (т. е. нахождению) на всех n элементарных отрезках [ x i- 1 , x i ] ( i =1, 2, … n ). Для того, чтобы система алгебраических уравнений имела решение, необходимо составить 4 n уравнений Первые 2 n уравнений получаются из условия , что график пройдет через заданные точки гд е, )()(3 1 2 11 iiiixxdxxcxxbax. Siixxx 1 32 1 )( )(1 iiiii iii hdhchbax. S yax. Si 1 iiixxh ni, . . . 2,
 23 Следующие ( n -1) уравнений вытекают из условия непрерывности первых производных в узлах интерполяции Приравнивая правые части в точка x = x i , получаем 2 1111 2 )(3)(2)( iiiiii xxdxxcbx. S dx d 1, . . . 2, 1 ni 2 132 iiiiiihdhcbb )()(1 iiiix. S dx d 1, . . . 2, 1 ni
23 Следующие ( n -1) уравнений вытекают из условия непрерывности первых производных в узлах интерполяции Приравнивая правые части в точка x = x i , получаем 2 1111 2 )(3)(2)( iiiiii xxdxxcbx. S dx d 1, . . . 2, 1 ni 2 132 iiiiiihdhcbb )()(1 iiiix. S dx d 1, . . . 2, 1 ni
 24 Следующие ( n -1) уравнений вытекают из условия непрерывности вторых производных в узлах интерполяции Приравнивая правые части в точка x = x i , получаем )(62)( 111 iiii xxdcx. S dx d 1, . . . 2, 1 ni iiiihdcc 31 )()(2 2 12 2 iiiix. S dx d 1, . . . 2, 1 ni
24 Следующие ( n -1) уравнений вытекают из условия непрерывности вторых производных в узлах интерполяции Приравнивая правые части в точка x = x i , получаем )(62)( 111 iiii xxdcx. S dx d 1, . . . 2, 1 ni iiiihdcc 31 )()(2 2 12 2 iiiix. S dx d 1, . . . 2, 1 ni
 25 На данном этапе у нас имеется 4 n неизвестных и (4 n -2) уравнений. Оставшиеся 2 уравнения можно получить из условия нулевой кривизны линии в концевых точках (условие свободного закрепления концов). Нулевая кривизна означает равенство нулю вторых производных в этих точках. Приравнивая правые части в точка x = x i , получаем 062 0 1 nnn hdcciiiihdcc 31 0)( 22 01 22 nn x. S dx d 1, . . . 2, 1 ni
25 На данном этапе у нас имеется 4 n неизвестных и (4 n -2) уравнений. Оставшиеся 2 уравнения можно получить из условия нулевой кривизны линии в концевых точках (условие свободного закрепления концов). Нулевая кривизна означает равенство нулю вторых производных в этих точках. Приравнивая правые части в точка x = x i , получаем 062 0 1 nnn hdcciiiihdcc 31 0)( 22 01 22 nn x. S dx d 1, . . . 2, 1 ni
 26 В результате получим nn nd c 3 01 1 iiya i iii i h cc d cch h yy b 3 2 3 1 11 1, . . . 2, 1 ni ni, . . . 2, 1 n nn nc h h yy b 3 21 1 211 111 32 i ii iiiii h yy chhchni, . . .
26 В результате получим nn nd c 3 01 1 iiya i iii i h cc d cch h yy b 3 2 3 1 11 1, . . . 2, 1 ni ni, . . . 2, 1 n nn nc h h yy b 3 21 1 211 111 32 i ii iiiii h yy chhchni, . . .
 27 The end
27 The end

