Численное решение уравнения с одной переменной Численное

Численное решение уравнения с одной переменной

Численное решение уравнения с одной переменной Решение практической задачи начинается с описания исходных данных и целей на языке строго определенных математических понятий. Точная формулировка условий и целей решения – это математическая постановка задачи. Наиболее существенные свойства реального объекта описываются с помощью математических соотношений. Данный способ решения называется построением математической модели. Модель – это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале. Процесс исследования свойств объекта по его модели называется моделированием. Математическая модель может иметь вид уравнения, системы уравнений либо быть выраженной в форме математических структур или соотношений. Математические модели могут быть непрерывными или дискретными. После моделирования проводится исследование математической модели, т. е. решение полученной математической задачи.

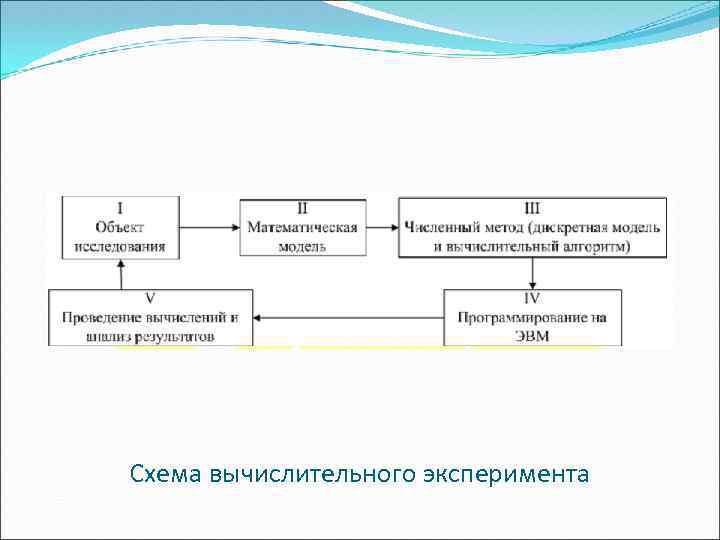Схема вычислительного эксперимента

Постановка задачи Многие задачи исследования различных объектов с помощью математических моделей, применения их для прогноза или расчета, приводят к необходимости решения нелинейных уравнений. Задача нахождения корней нелинейных уравнений вида F(x)=0; встречается в разделах физики, механики, строительства. Необходимым элементом решения этих задач является решение уравнений. Но большинство их не могут быть решены аналитически. Применяются численные методы, которые позволяют решать множество уравнений, недоступных для аналитических методов. Пусть функция F(x) определена и непрерывна на конечном интервале [a, b ]. Всякое число ξ ∈ [a, b ], обращающее функцию F(x) в нуль, т. е. F(ξ )=0, называется корнем уравнения.

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Такими методами решались уравнения из школьной программы. Подавляющее большинство нелинейных уравнений с одной переменной не решается путем аналитических преобразований (прямыми методами), поэтому на практике они решаются только численными методами. Решить такое уравнение – значит установить наличие корней, их число и найти значения этих корней с заданной точностью. При решении задачи численного нахождения действительных корней (комплексные корни нерассматриваются) уравнения выделяют два этапа: 1) отделение корней, т. е. определение интервалов, в каждом из которых содержится только один корень уравнения; 2) уточнение корней, т. е. вычисление их с заданной степенью точности.

Отделение корней производится графически или аналитически. Корни уравнения F(x) – это точки пересечения графика функции F(x)с осью абсцисс. Достаточно построить график функции F(x) и отметить на оси абсцисс отрезки, содержащие по одному корню. Графический способ применяется часто. Обычно с него и начинают отделение корней. Но он не обладает большой точностью: − когда интервал, содержащий корень, небольшой длины или корни расположены близко, можно ошибиться в его выборе; − когда графики функций расположены близко и трудно установить их пересечение. В этих случаях графическое пересечение корней необходимо проверить и уточнить.

Основу аналитического способа отделения корней составляет известная из курса математического анализа теорема Больцано-Коши. Пусть функция F(x)непрерывна на отрезке [a, b] и на концах отрезка принимает значения разных знаков, т. е. F(a)*F(b)< 0. Тогда существует такая точка ξ, принадлежащая интервалу (а, b), в которой функция обращается в ноль, т. е. F(ξ)=0. Корень будет единственным, если F' (x) (или F'' (x) ) существует и сохраняет знак на рассматриваемом отрезке.

Метод половинного деления Это один из простейших методов нахождения корней нелинейного уравнения. Будем считать, что отрезок [a, b], на котором расположен единственный искомый корень, уже найден. х =c – это единственный корень на отрезке [a, b], т. е. с∈ [a, b]. За начальное приближение принимаем середину этого отрезка: Исследуем значения функции F(x) на концах отрезков [a, co] и [co, b] , т. е. в точках а, сo, b. Тот из отрезков, на концах которого F(x) принимает значения разных знаков, содержит искомый корень, поэтому его принимаем в качестве нового отрезка [a 1, b 1 ]. Вторую половину отрезка [a, b ] , на которой знак F(x) не меняется, отбрасываем. В качестве первого приближения корня уравнения F(x) принимаем середину нового отрезка:

Получим последовательность приближений {c 1, c 2, …. ck } т. е. k-е приближение вычисляется как После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое. Пусть требуется найти приближенное решение X* с точностью до некоторого заданного малого числа ε> 0 : Метод половинного деления всегда сходится, и полученное решение может иметь любую наперед заданную точность. Однако, этот метод не позволяет быстро получить результат. Итерационный процесс можно завершать тогда, когда значение функции F(x) после k-й итерации станет меньшим по модулю ε , т. е

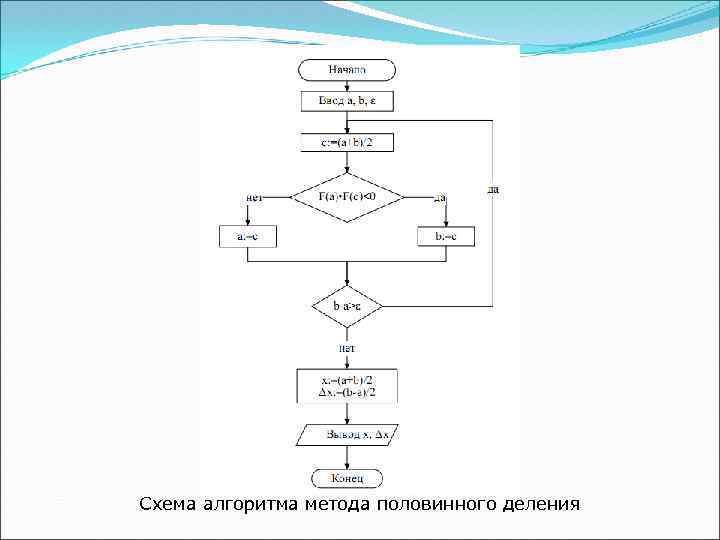Схема алгоритма метода половинного деления

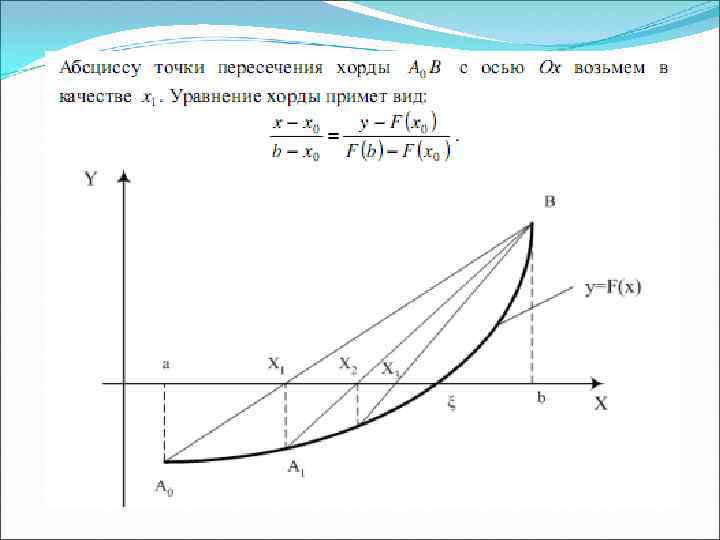
Метод хорд Это метод последовательных приближений. Приближения к корню находятся так: если известно предыдущее приближение Xn(n=0, 1, 2…. ), то последующее приближение Xn+1 вычисляется по формуле: где Р – некоторое выражение, устанавливающее связь между предыдущим и последующим приближениями. Начинается процесс с какого-либо числа Xo из отрезка изоляции корня – начального приближения. Формула называется рекуррентной. Такая формула позволяет выразить (n+1)-й член последовательности через несколько предыдущих его членов. При наличии рекуррентной формулы последовательность полностью определяется выбором начального приближения Xo. Получаемая с помощью рекуррентной формулы последовательность приближений называется итерационной последовательностью.

Итерация – неоднократное применение какой-нибудь операции, в данном случае – это вычисления по рекуррентной формуле. Построим итерационную последовательность. За начальное приближение Xo в методе хорд принимается конец отрезка, противоположный с, где с – один из концов отрезка [a, b ] , удовлетворяющий условию Тогда Xo=a, соединим точки отрезком (хордой)