Численное решение систем нелинейных уравнений С Н У



















3_snu_1.ppt
- Размер: 226.0 Кб
- Автор: Людмила Казанович
- Количество слайдов: 21
Описание презентации Численное решение систем нелинейных уравнений С Н У по слайдам
 Численное решение систем нелинейных уравнений С Н У
Численное решение систем нелинейных уравнений С Н У
 Общий вид СНУ где FF – функции нескольких переменных, хх – неизвестные nn – – порядок системы 0), , , , , ( 21 21 212 211 njn nji nj nj xxxx.
Общий вид СНУ где FF – функции нескольких переменных, хх – неизвестные nn – – порядок системы 0), , , , , ( 21 21 212 211 njn nji nj nj xxxx.
 Методы решения СНУ: 1. 1. Прямых методов для решения СНУ не существует. . 2. 2. Итерационные методы. Методы являются неустойчивыми , однако точность полученного решения определяется пользователем. .
Методы решения СНУ: 1. 1. Прямых методов для решения СНУ не существует. . 2. 2. Итерационные методы. Методы являются неустойчивыми , однако точность полученного решения определяется пользователем. .
 Метод Зейделя (метод простых итераций) Ограниченный круг СНУ Исходные данные: 1. 1. FFii (( xx 11 , x, x 22 , …, xnn )) 2. 2. ХХ (0)(0) 3. 3. ЕЕ
Метод Зейделя (метод простых итераций) Ограниченный круг СНУ Исходные данные: 1. 1. FFii (( xx 11 , x, x 22 , …, xnn )) 2. 2. ХХ (0)(0) 3. 3. ЕЕ
 Требование Функции FF ii (( xx 11 , x, x 22 , …, x nn )) должны быть непрерывны в окрестности точки истинного решения Х и точки начального приближения ХХ (0)(0)
Требование Функции FF ii (( xx 11 , x, x 22 , …, x nn )) должны быть непрерывны в окрестности точки истинного решения Х и точки начального приближения ХХ (0)(0)
 Метод Зейделя на примере СНУ 3 -го порядка 1. 1. Из 1 -го уравнения выражаем неизвестное х11. . 2. 2. Из 2 -го уравнения выражаем неизвестное х 22. . 3. 3. Из 3 -го уравнения выражаем неизвестное х 33. . 0), , ( 3213 3212 3211 xxx.
Метод Зейделя на примере СНУ 3 -го порядка 1. 1. Из 1 -го уравнения выражаем неизвестное х11. . 2. 2. Из 2 -го уравнения выражаем неизвестное х 22. . 3. 3. Из 3 -го уравнения выражаем неизвестное х 33. . 0), , ( 3213 3212 3211 xxx.
 Получим новую систему: 2. В правую часть 1 -го уравнения подставляем начальные приближения неизвестных х 22 (0)(0) и х 33 (0)(0). Получаем уточненное значение неизвестного хх 11 (1)(1). . 3. В правую часть 2 -го уравнения подставляем начальное приближение неизвестного х 33 (0)(0) и уточненное значение х 11 (1)(1). Получаем уточненное значение неизвестного х 22 (1)(1). . 4. В правую часть 3 -го уравнения подставляем уточненные значения неизвестных х 11 (1)(1) и х 22 (1)(1). Получаем уточненное значение неизвестного хх 33 (1)(1). . ), ( 2133 3122 3211 xxx xxx
Получим новую систему: 2. В правую часть 1 -го уравнения подставляем начальные приближения неизвестных х 22 (0)(0) и х 33 (0)(0). Получаем уточненное значение неизвестного хх 11 (1)(1). . 3. В правую часть 2 -го уравнения подставляем начальное приближение неизвестного х 33 (0)(0) и уточненное значение х 11 (1)(1). Получаем уточненное значение неизвестного х 22 (1)(1). . 4. В правую часть 3 -го уравнения подставляем уточненные значения неизвестных х 11 (1)(1) и х 22 (1)(1). Получаем уточненное значение неизвестного хх 33 (1)(1). . ), ( 2133 3122 3211 xxx xxx
 5. Далее рассчитывается разность между значениями начальных приближений и уточненными значениями неизвестных. Если то считается, что значения х 11 (1)(1). , х 22 (1)(1). , х 33 (1)(1) являются решением данной системы. В противном случае эти значения принимаются за начальное приближение и процесс повторяется. Exx и Exx )0( 3 )1( 3 )0( 2 )1( 2 )0( 1 )1(
5. Далее рассчитывается разность между значениями начальных приближений и уточненными значениями неизвестных. Если то считается, что значения х 11 (1)(1). , х 22 (1)(1). , х 33 (1)(1) являются решением данной системы. В противном случае эти значения принимаются за начальное приближение и процесс повторяется. Exx и Exx )0( 3 )1( 3 )0( 2 )1( 2 )0( 1 )1(
 ЗАМЕЧАНИЕ Метод Зейделя применим, если неизвестные из соответствующих уравнений можно выразить в явном виде. . Метод Зейделя для решения СНУ не является универсальным.
ЗАМЕЧАНИЕ Метод Зейделя применим, если неизвестные из соответствующих уравнений можно выразить в явном виде. . Метод Зейделя для решения СНУ не является универсальным.
 Примеры: 12 3 21 21 3 2 2 1 ln 5, 0 41 012 ln 014 xx xx ? ? 0 ln 42 ln 0 cos 10 sin 4 2 1 2 2221 21 3 2 2 1 x x xxxx
Примеры: 12 3 21 21 3 2 2 1 ln 5, 0 41 012 ln 014 xx xx ? ? 0 ln 42 ln 0 cos 10 sin 4 2 1 2 2221 21 3 2 2 1 x x xxxx
 Метод Ньютона для решения СНУ Основа: разложение функций в ряд Тейлора относительно значений начальных приближений неизвестных. Затем применяется линеаризация системы.
Метод Ньютона для решения СНУ Основа: разложение функций в ряд Тейлора относительно значений начальных приближений неизвестных. Затем применяется линеаризация системы.
 Для реализации метода Ньютона необходимо задать следующие данные: 1. Выражения для функций FF 11 , F, F 22 , , …, …, F Fnn в в аналитическом виде. 2. Выражения для частных производных функций FF 11 , F, F 22 , , …, …, F Fnn по каждому аргументу в аналитическом виде. 3. 3. xx 11 00 , x, x 22 00 , …, x nn 00. . 4. Е.
Для реализации метода Ньютона необходимо задать следующие данные: 1. Выражения для функций FF 11 , F, F 22 , , …, …, F Fnn в в аналитическом виде. 2. Выражения для частных производных функций FF 11 , F, F 22 , , …, …, F Fnn по каждому аргументу в аналитическом виде. 3. 3. xx 11 00 , x, x 22 00 , …, x nn 00. . 4. Е.
 Требование Функции FF ii (( xx 11 , x, x 22 , …, x nn )) должны быть непрерывны и дифференцируемы в окрестности точки истинного решения Х и точки начального приближения ХХ (0)(0)
Требование Функции FF ii (( xx 11 , x, x 22 , …, x nn )) должны быть непрерывны и дифференцируемы в окрестности точки истинного решения Х и точки начального приближения ХХ (0)(0)
 Метод Ньютона на примере СНУ 3 -го порядка Задано: xx 11 00 , x, x 22 00 ии x x 33 00. . Истинное решение системы: xx 11 , x, x 22 ии x x 33. . Разность: xx 11 =x=x 11 -x-x 11 00 , , xx 22 =x=x 22 -x-x 22 00 , , xx 33 =x=x 33 -x-x 33 00 0), , ( 3213 3212 3211 xxx.
Метод Ньютона на примере СНУ 3 -го порядка Задано: xx 11 00 , x, x 22 00 ии x x 33 00. . Истинное решение системы: xx 11 , x, x 22 ии x x 33. . Разность: xx 11 =x=x 11 -x-x 11 00 , , xx 22 =x=x 22 -x-x 22 00 , , xx 33 =x=x 33 -x-x 33 00 0), , ( 3213 3212 3211 xxx.
 FF 11 , F, F 22 ии F F 33 разлагаются в ряд Тейлора. Члены, содержащие производные старше первого порядка отбрасываются. 0), , (), , ( 0), , ( 3 3 3 2 2 3 1 1 30 30 20 133213 3 3 2 2 1 1 20 30 20 123212 3 3 1 2 2 1 10 30 20 113211 x x F x x F xxx. Fxxx. F x x F xxx. F Преобразуем систему.
FF 11 , F, F 22 ии F F 33 разлагаются в ряд Тейлора. Члены, содержащие производные старше первого порядка отбрасываются. 0), , (), , ( 0), , ( 3 3 3 2 2 3 1 1 30 30 20 133213 3 3 2 2 1 1 20 30 20 123212 3 3 1 2 2 1 10 30 20 113211 x x F x x F xxx. Fxxx. F x x F xxx. F Преобразуем систему.
 Получим систему линейных алгебраических уравнений: Неизвестные — xx 11 , , xx 2 2 и и xx 33 , , Вектор-столбец свободных членов – FF 11 , F, F 22 ии F F 33 в в точке начального приближения, Коэффициенты — производные функций FF 11 , F, F 22 ии F F 33 по по неизвестным xx 11 , x, x 22 ии x x 33 в точке начального приближения. ), , ( 0 3 0 2 0 133 3 3 2 2 3 1 1 3 0 2 0 123 3 2 2 1 1 2 0 3 0 2 0 113 3 1 2 2 1 1 xxx. Fx x F x x F xxx. Fx x
Получим систему линейных алгебраических уравнений: Неизвестные — xx 11 , , xx 2 2 и и xx 33 , , Вектор-столбец свободных членов – FF 11 , F, F 22 ии F F 33 в в точке начального приближения, Коэффициенты — производные функций FF 11 , F, F 22 ии F F 33 по по неизвестным xx 11 , x, x 22 ии x x 33 в точке начального приближения. ), , ( 0 3 0 2 0 133 3 3 2 2 3 1 1 3 0 2 0 123 3 2 2 1 1 2 0 3 0 2 0 113 3 1 2 2 1 1 xxx. Fx x F x x F xxx. Fx x
 СЛАУ решается любым известным методом (метод Гаусса, метод Крамера), получаем значения неизвестных xx 11 , , xx 2 2 и и xx 33 xx 11 , x, x 22 ии x x 33 рассчитываются по формулам: xx 11 =x=x 11 00 ++ xx 11 , , xx 22 =x=x 22 00 ++ xx 22 , , xx 33 =x=x 33 00 ++ xx 333 3 2 3 1 3 3 2 2 2 1 2 3 1 2 1 1 1 x. F x. F A ), , ( 0 3 0 2 0 13 0 2 0 12 0 3 0 2 0 11 xxx. F B Матрица Якоби (Якобиан)
СЛАУ решается любым известным методом (метод Гаусса, метод Крамера), получаем значения неизвестных xx 11 , , xx 2 2 и и xx 33 xx 11 , x, x 22 ии x x 33 рассчитываются по формулам: xx 11 =x=x 11 00 ++ xx 11 , , xx 22 =x=x 22 00 ++ xx 22 , , xx 33 =x=x 33 00 ++ xx 333 3 2 3 1 3 3 2 2 2 1 2 3 1 2 1 1 1 x. F x. F A ), , ( 0 3 0 2 0 13 0 2 0 12 0 3 0 2 0 11 xxx. F B Матрица Якоби (Якобиан)
 Если полученные значения x 1 и x 2 и x 3 по по модулю оказались менее заданной точности Е, то считается, что рассчитанные значения xx 11 , x, x 22 ии x x 33 являются решением данной системы нелинейных уравнений. Если хотя бы одно из значений x 1 , x 2 , x 3 по по модулю оказалось выше заданной точности Е, то рассчитанные значения xx 11 , x, x 22 ии x x 33 принимаются в качестве нового начального приближения и процесс повторяется.
Если полученные значения x 1 и x 2 и x 3 по по модулю оказались менее заданной точности Е, то считается, что рассчитанные значения xx 11 , x, x 22 ии x x 33 являются решением данной системы нелинейных уравнений. Если хотя бы одно из значений x 1 , x 2 , x 3 по по модулю оказалось выше заданной точности Е, то рассчитанные значения xx 11 , x, x 22 ии x x 33 принимаются в качестве нового начального приближения и процесс повторяется.
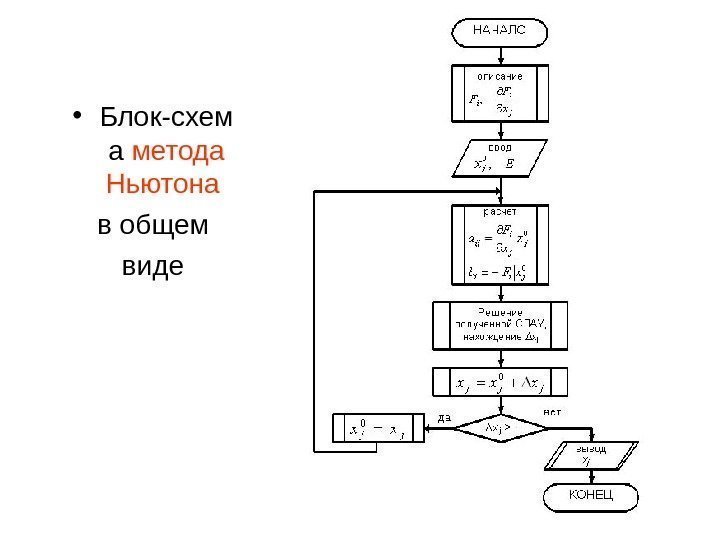
 • Блок-схем а метода Ньютона в общем виде
• Блок-схем а метода Ньютона в общем виде
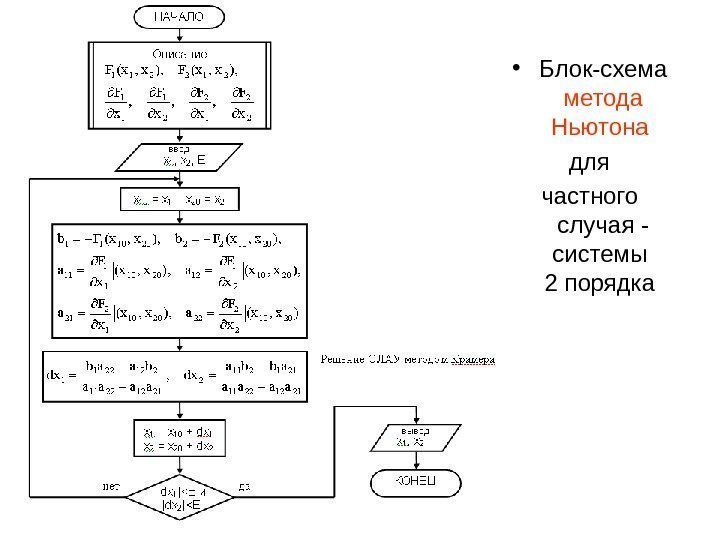
 • Блок-схема метода Ньютона для частного случая — системы 2 порядка
• Блок-схема метода Ньютона для частного случая — системы 2 порядка
 Замечание Метод Ньютона является неустойчивым , , прогнозировать сходимость невозможно. . Сходимость метода зависит от порядка системы и от удачного выбора начального приближения решения.
Замечание Метод Ньютона является неустойчивым , , прогнозировать сходимость невозможно. . Сходимость метода зависит от порядка системы и от удачного выбора начального приближения решения.
