ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ Игнатюк В.И. Игнатов А.Ю. Производная функции

ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ Игнатюк В.И. Игнатов А.Ю.

Производная функции : где: Если Δx принять равным конечному числу, то:

Это соотношение представляет аппроксимацию производной с помощью конечных разностей. При этом шаг аргумента Δx, то есть разность между соседними значениями аргумента, обычно принимают одинаковым и обозначают для краткости одной буквой: h или λ.

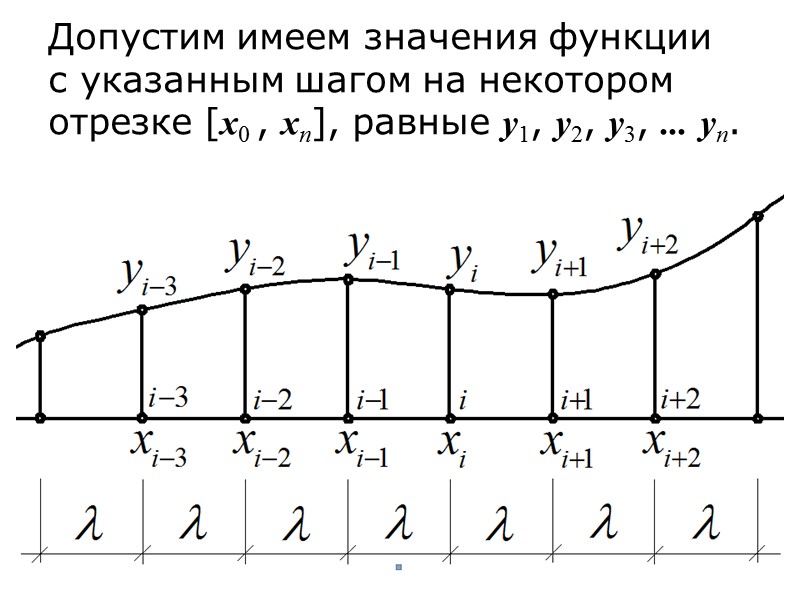
Допустим имеем значения функции с указанным шагом на некотором отрезке [x0 , xn], равные y1, y2, y3, ... yn.

Запишем выражение для производной в точке i (при x = xi). При этом в зависимости от способа вычисления конечных разностей получим разные формулы для вычисления производной в одной и той же точке:

а) для левой разности будем иметь: б) для правой разности получим: в) для центральной разности:

Учитывая, что для центральной разности берется участок большей длины ( 2λ ), то эта разность будет иметь большие погрешности, чем первые две, и соответственно требует разбивки системы на более мелкие участки. Однако она приводит к симметричным уравнениям и поэтому используется довольно часто.

Для второй производной в точке i будем иметь: а) слева через правые разности:

б) справа через левые разности:

Для третьей производной в точке i получим: а) слева (левая разность):

б) справа (правая разность):

Для четвертой производной: а) слева – через правые :

б) справа – через левые : Можно заметить, что четные производные одинаковы слева и справа.

МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ

Для описания задач строительной механики и теории упругости часто используются дифференциальные уравнения равновесия, выражаемые через перемещения (прогибы) систем. При обычном решении таких уравнений ищется функция перемещений, описывающая состояние системы и удовлетворяющая условиям задачи, включая её граничные условия.

В методе конечных разностей (МКР) находится не сама функция, а её значения в некоторых точках (узлах). Понятно, что густота разбивки системы ( λ = Δx ) здесь определяет точность решения.

Дифференциальные уравнения равновесия, выражаемые относительно прогибов для стержней могут быть представлены в следующих видах: 1)

2) известно, что получим: 3) если уравнение из пункта 1 продифференцировать два раза с учетом пункта 2 получим:

При записи производных для граничных точек сооружений, будут появляться точки, расположенные за пределами сооружения, или так называемые законтурные точки.

Для их определений используются обычно граничные условия для сооружений, то есть известные значения физических величин на границах сооружения, связанные с закреплением или незакреплением этих точек. Рассмотрим ряд граничных условий:

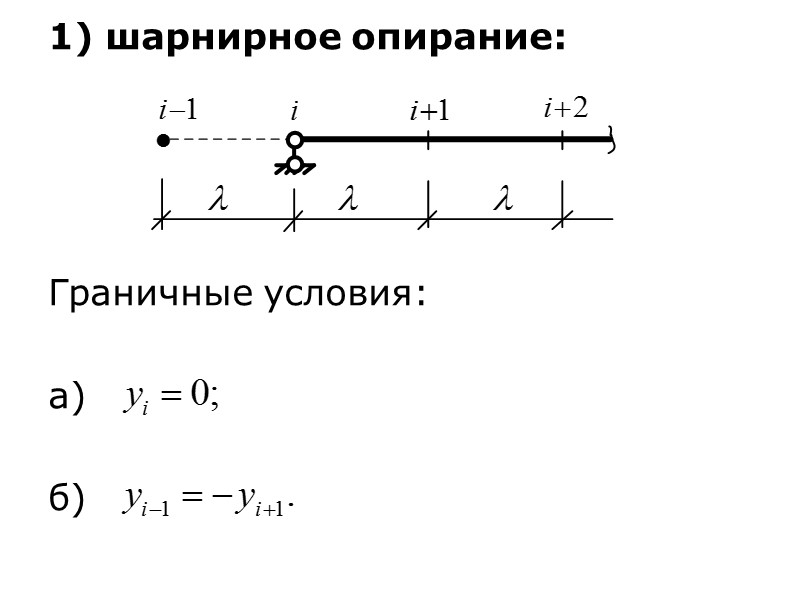
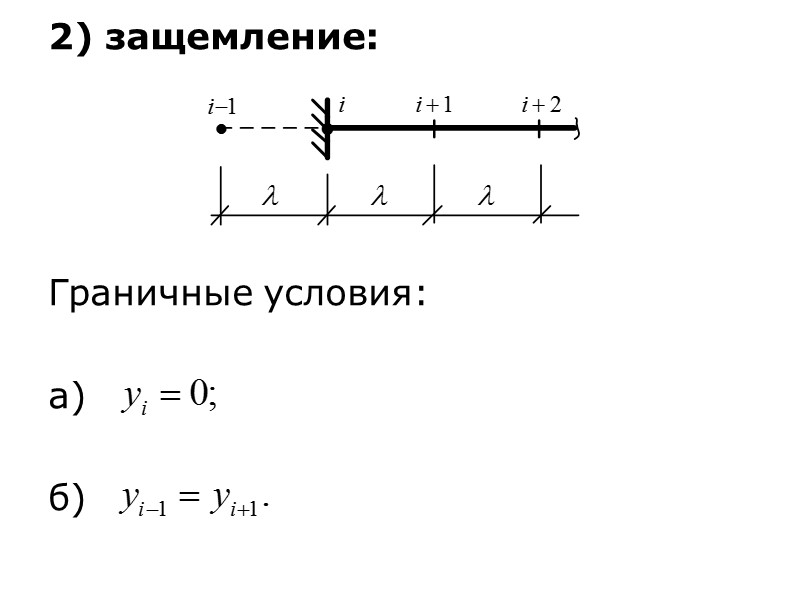
1) шарнирное опирание: Граничные условия: а) б)

2) защемление: Граничные условия: а) б)

3) свободный край: Граничные условия: Если m или P отсутсвуют на краю, то соответств. правые части равны нулю.