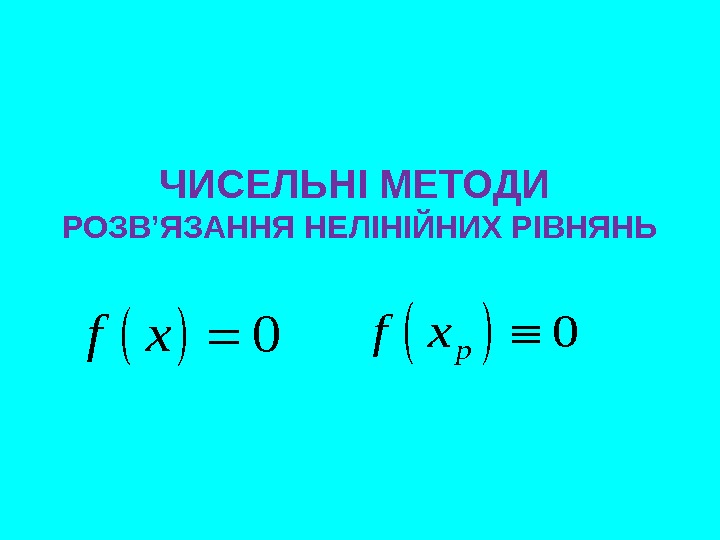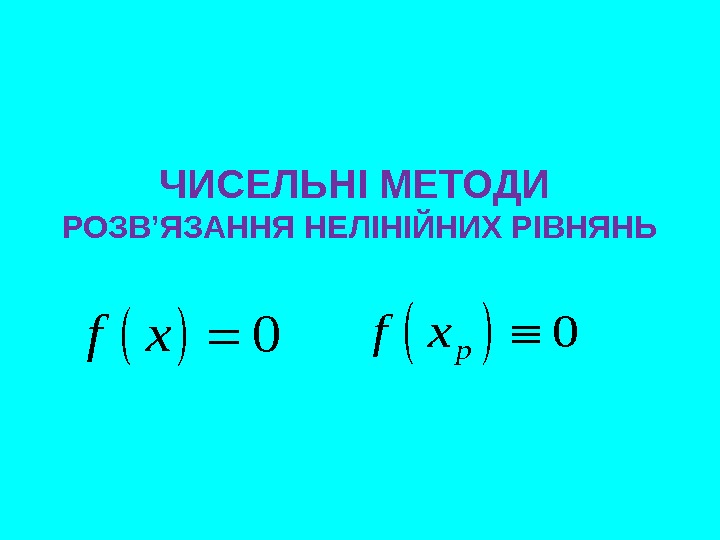ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ НЕЛІНІЙНИХ РІВНЯНЬ 0 f x

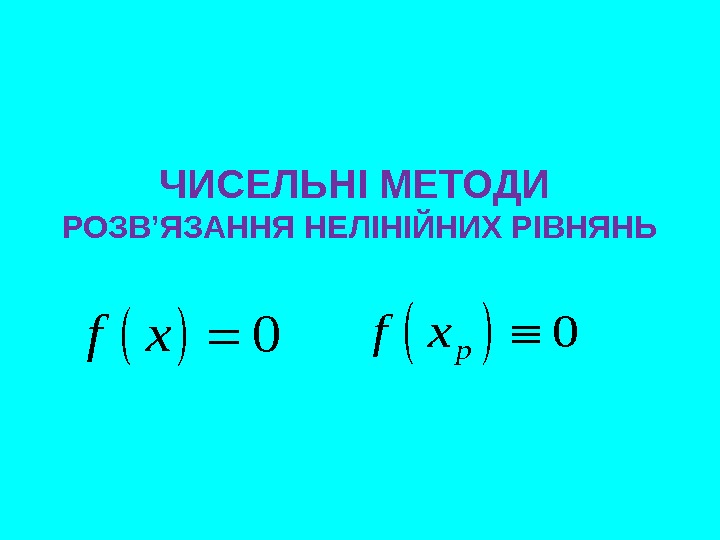ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ НЕЛІНІЙНИХ РІВНЯНЬ 0 f x 0 p f x

ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ НЕЛІНІЙНИХ РІВНЯНЬ 1) Локалізувати корінь a < xp < b ознака: 2) Уточнити корінь до припустимої похибки δ x < ε 0 , f a f b x a b 2 2 p a b x

МЕТОДИ УТОЧНЕННЯ КОРЕНЯ

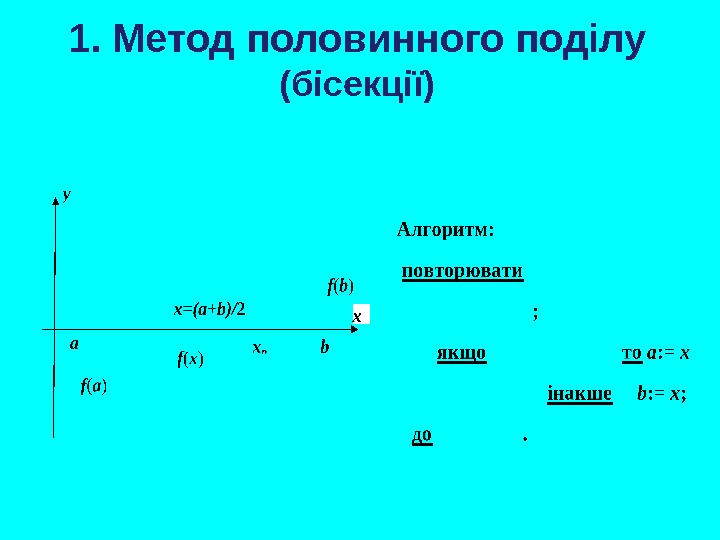1. Метод половинного поділу (бісекції)

2. Метод хорд

3. Метод Ньютона (дотичних) лінеаризація рівняння 0 0 0 0 f x f x x x f x

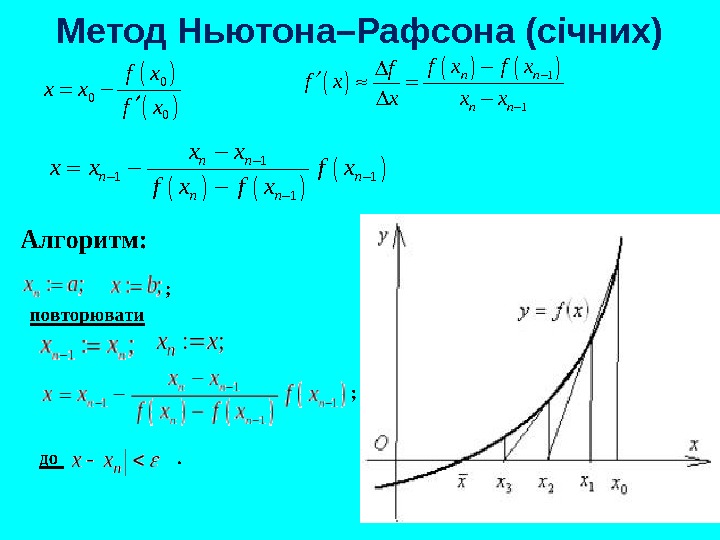Метод Ньютона–Рафсона (січних) 1 1 n n n nf x f f x x 1 1 n n n x x f x f x 0 0 0 f x x x f x

5. Метод простої ітерації 0 f x x x 1 0 2 1 1, , . . n nx x x Якщо існує границя послідовності x n то x n → x р. Умова збіжності: 1 1 1 0 1 n n n n n x x x

Метод простої ітерації геометрична інтерпретація