ЧЕТЫРЁХУГОЛЬНИКИ 8 класс ПАРАЛЛЕЛОГРАММ ПРЯМОУГОЛЬНИК РОМБ КВАДРАТ ТРАПЕЦИЯ
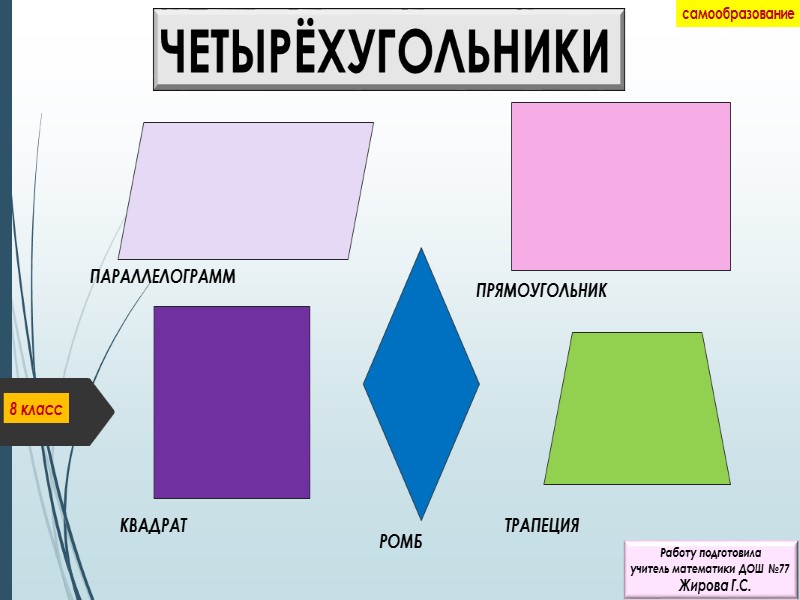
ЧЕТЫРЁХУГОЛЬНИКИ 8 класс ПАРАЛЛЕЛОГРАММ ПРЯМОУГОЛЬНИК РОМБ КВАДРАТ ТРАПЕЦИЯ самообразование Работу подготовила учитель математики ДОШ №77 Жирова Г.С.
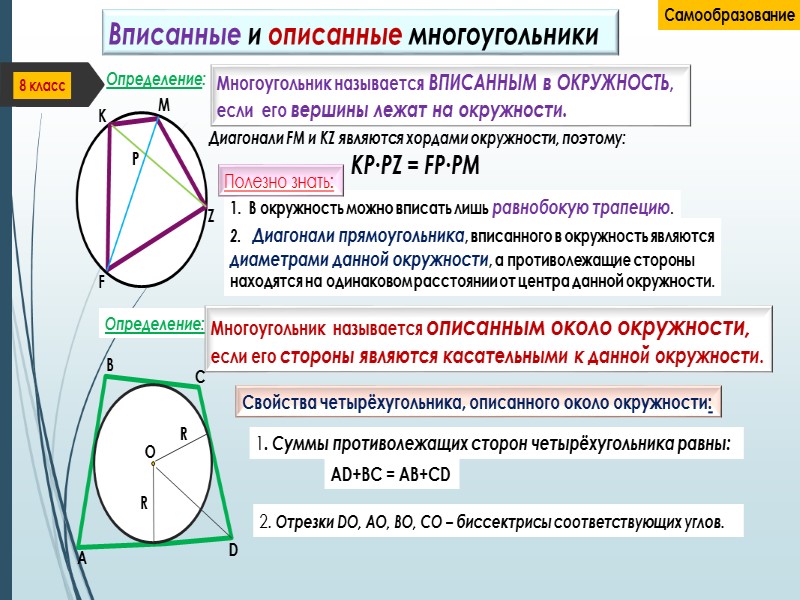
Определение: 8 класс Выпуклый четырёхугольник – это геометрическая фигура, которая состоит из четырёх точек, каждые три из которых не лежат на одной прямой, и четырёх отрезков, последовательно соединяющих эти точки без взаимных пересечений, причём вся фигура расположена в одной полуплоскости относительно прямой, содержащей любую из её сторон. Диагонали четырёхугольника – это отрезки, которые соединяют две не соседние вершины четырёхугольника. А В С D FKLM - данный четырёхугольник. FL, KM – его диагонали Определение: Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны, то есть, лежат на параллельных прямых. F K L M ABCD – параллелограмм: AB║CD; ВС║AD AC, BD – его диагонали; точка О – точка пересечения диагоналей. O


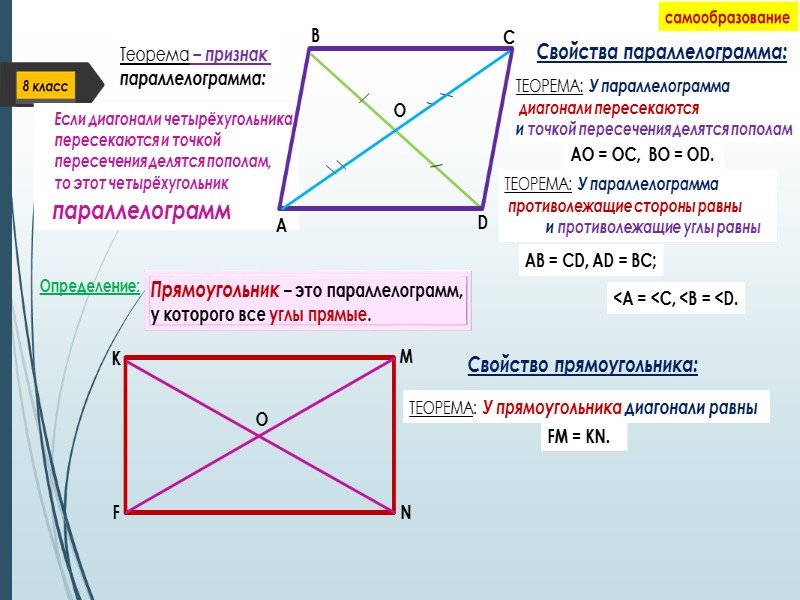
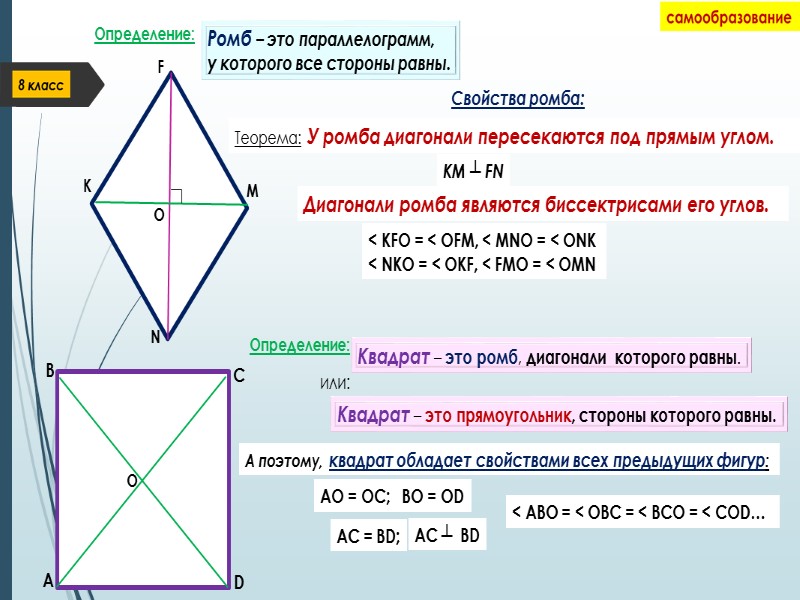
Определение: Ромб – это параллелограмм, у которого все стороны равны. Свойства ромба: Теорема: У ромба диагонали пересекаются под прямым углом. F K M N O KM ┴ FN Определение: Квадрат – это ромб, диагонали которого равны. или: Квадрат – это прямоугольник, стороны которого равны. A B C D А поэтому, квадрат обладает свойствами всех предыдущих фигур: О АО = ОС; ВО = ОD AC ┴ BD AC = BD; Диагонали ромба являются биссектрисами его углов. < KFO = < OFM, < MNO = < ONK < NKO = < OKF, < FMO = < OMN < ABO = < OBC = < BCO = < COD…
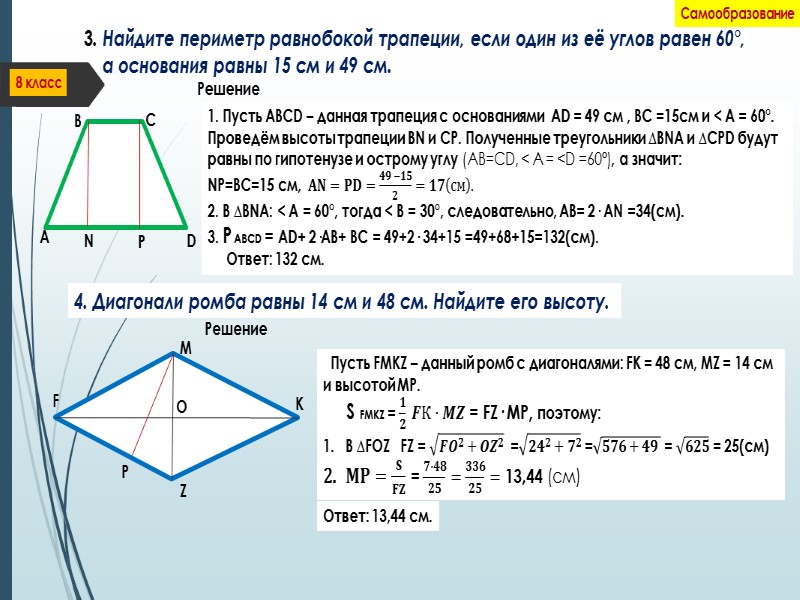
8 класс Самообразование Зная свойства перечисленных фигур, можно успешно решать задачи как вычислительного характера, так и на доказательства. 1. Один из углов параллелограмма равен 83° . Найдите остальные его углы. Решение Пусть ABCD – данный параллелограмм, у которого < А= 83°, тогда : так как противолежащие углы параллелограмма равны, то < С= < А= 83°, а так как сумма углов параллелограмма, прилежащих к его стороне равна 180°, то: < В = 180° – 83° = 97° , следовательно, < D = < В = 97° , как ему противолежащий. Ответ: 97°, 83°, 97°. A B C D 2. Два угла трапеции равны 36° и 112° . Найдите её остальные углы. Решение F K M Z Пусть FKMZ – данная трапеция, угол KFZ которой равен 36°. Так как < F +< K = 180°, как внутренние односторонние при FZ║ KM и FK – секущей, то <К = 180°-36° = 144°. Если < М = 112°, то < Z = 180° - 112°= 68°, так как < М и < Z внутренние односторонние при FZ║ KM и MZ – секущей. Ответ: 144°, 68°.
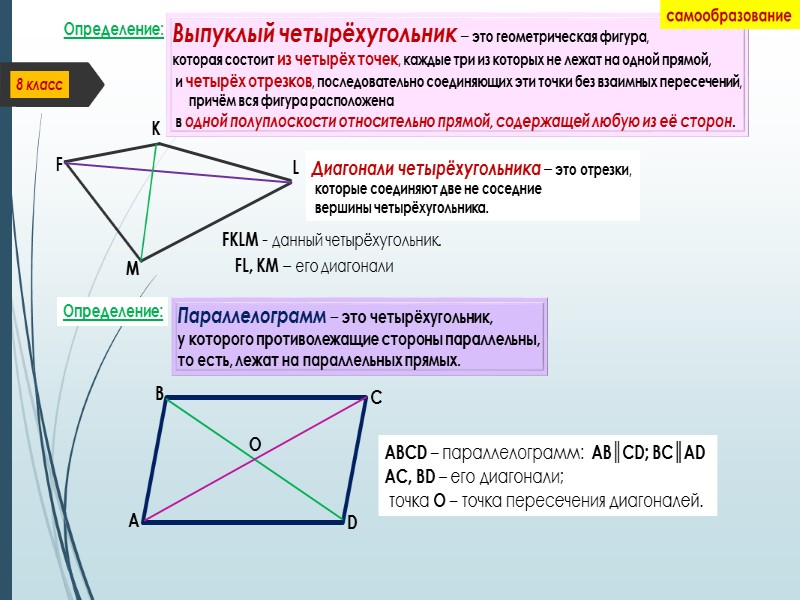
Самообразование Вписанные и описанные многоугольники Определение: Многоугольник называется ВПИСАННЫМ в ОКРУЖНОСТЬ, если его вершины лежат на окружности. F 8 класс Диагонали FM и KZ являются хордами окружности, поэтому: KP∙PZ = FP∙PM K M P Z Определение: Многоугольник называется описанным около окружности, если его стороны являются касательными к данной окружности. A B C D R O R Свойства четырёхугольника, описанного около окружности: 1. Суммы противолежащих сторон четырёхугольника равны: AD+BC = AB+CD 1. В окружность можно вписать лишь равнобокую трапецию. 2. Диагонали прямоугольника, вписанного в окружность являются диаметрами данной окружности, а противолежащие стороны находятся на одинаковом расстоянии от центра данной окружности. Полезно знать: 2. Отрезки DO, AO, BO, CO – биссектрисы соответствующих углов.
8 класс Самообразование 7. Периметр описанной трапеции равен 28 см, а отрезок средней линии трапеции, расположенный между её диагоналями, равен 3 см. найдите основания трапеции. Решение A B C D F K Пусть ABCD – данная трапеция периметр которой равен 28 см, и FK – отрезок её средней линии, равный 3 см. По свойству описанной около окружности трапеции имеем: AD+BC=AB+CD= 14 см. Тогда ZM = 7 см. Так как ZM – средняя линия трапеции, то ZF – средняя линия ∆ABC, KM – средняя линия ∆DCB, а значит, ZF+KM= BC, следовательно, BC = 7 – 3 = 4(см), тогда AD = 14 – 4 = 10(см). Z M Ответ: 10 см, 4 см. 8. Через точку пересечения диагоналей квадрата провели две взаимно перпендикулярные прямые. Докажите, что точки пересечения этих прямых со сторонами квадрата являются вершинами другого квадрата. A B C D F K M Z O Пусть FKMZ – данный квадрат, точка O – точка пересечения его диагоналей, а точки A,B,C,D – точки пересечения двух перпендикулярных прямых AC и BD со сторонами квадрата, проходящих через точку О. Пусть образовавшийся < МОС равен δ, тогда < ZOD = < FOA =

8 класс Самообразование Конечно же, чтобы усвоить данную тему, необходимо решить много задач на применение свойств рассматриваемых фигур. Приведённых примеров явно не достаточно для качественного усвоения темы. Здесь лишь обозначены пути решения задач с конкретными условиями. И приведённые решения не являются единственными решениями, а лишь представляют один из способов решения данной задачи, так что Ваше решение может быть более рациональным, что и будет свидетельствовать о качестве усвоения темы. В предложенной работе намеренно не приводились доказательства свойств фигур, носящих ранг теорем, в надежде, что это вполне доступно выполнить и самостоятельно. Если, на первых порах, доказательство какой-нибудь теоремы вызовет затруднение, то можете пользоваться формулировкой теоремы как известным фактом и применять его при решении задач. Успехов Вам. И помните: ЗНАНИЯ ЛИШЬ ТОГДА БУДУТ ПРОЧНЫМИ, ЕСЛИ ОНИ ПРИОБРЕТЕНЫ СОБСТВЕННЫМИ УСИЛИЯМИ.


164-chetyrehugolyniki_8_kl.pptx
- Количество слайдов: 12
