Часть 2. КИНЕМАТИКА Кинематика – раздел

Часть 2. КИНЕМАТИКА Кинематика – раздел механики, в котором изучаются геометрические свойства движения тел без учета их инерции и действующих на них сил. Основные задачи кинематики: 1. установить способ задания движения точки или тела как функцию положения их в заданной системе координат в любой момент времени. 2. зная закон движения точки (тела), описать параметры движения (перемещение, скорость, ускорение): а) точки; б) тела в целом и каждой точки тела в отдельности.

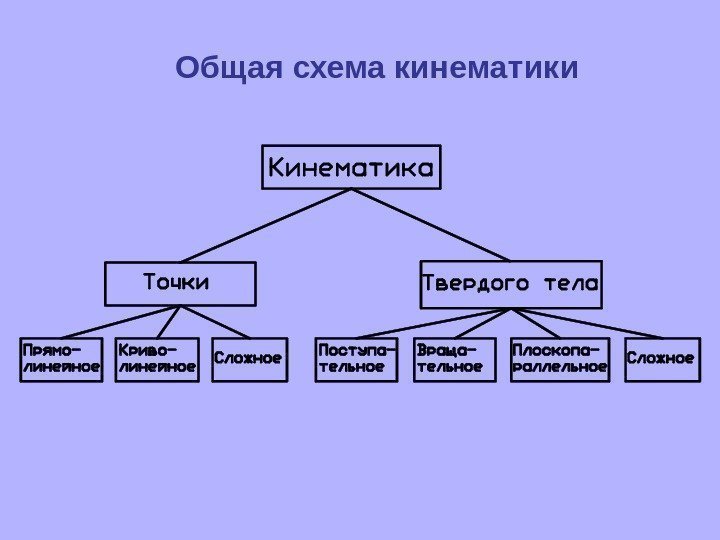
Общая схема кинематики

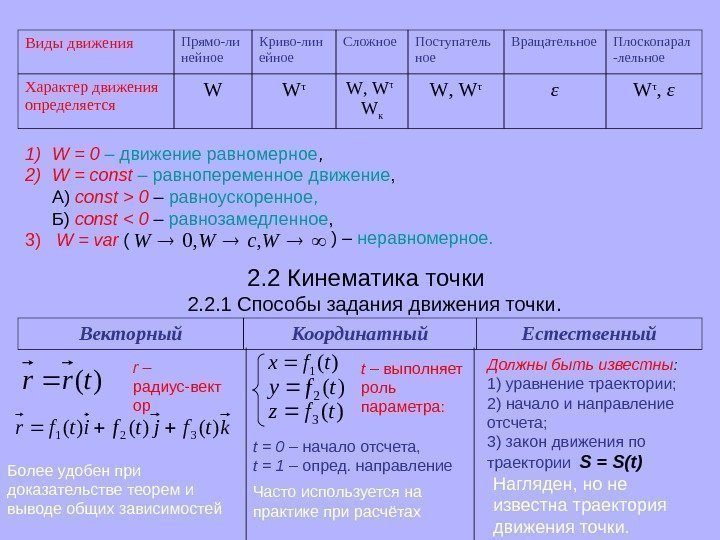
Виды движения Прямо-ли нейное Криво-лин ейное Сложное Поступатель ное Вращательное Плоскопарал -лельное Характер движения определяется W W τ W , W τ W к W , W τ ε W τ , ε 1) W = 0 – движение равномерное , 2) W = const – равнопеременное движение , А) const > 0 – равноускоренное, Б) const < 0 – равнозамедленное , 3) W = var (Wc. WW, , 0 ) – неравномерное. 2. 2 Кинематика точки Векторный Координатный Естественный 2. 2. 1 Способы задания движения точки. )(trr r – радиус-вект ор ktfjtfitfr )()()( 321 Более удобен при доказательстве теорем и выводе общих зависимостей )(1 tfх )(2 tfy )(3 tfz t – выполняет роль параметра: t = 0 – начало отсчета, t = 1 – опред. направление Часто используется на практике при расчётах Должны быть известны : 1) уравнение траектории; 2) начало и направление отсчета; 3) закон движения по траектории S = S ( t ) Нагляден, но не известна траектория движения точки.

Векторный Координатный Естественный r dt rd v kzjyixv x dt dx vx y dt dy vy z dt dz vz v vxcos vv y cos v v z cos 222 zyxvvvv S dt d. S v V – модуль скорости точки. Направлен по касательной к траектории точки. vr dt dv dt rd w 2 2 Направлено в сторону вогнутости траектории. kzjyix. W kvjvivzyx x. VWxx y. VWyy z. VWzz W Wx 1 cos W Wy 1 cos W Wz 1 cos 222 zyx. WWWW v. SW — полностью не характеризует W. dt dv W W Wcos 2 v Wn W Wncos 22 n. WWW — радиус кривизны траектории движения

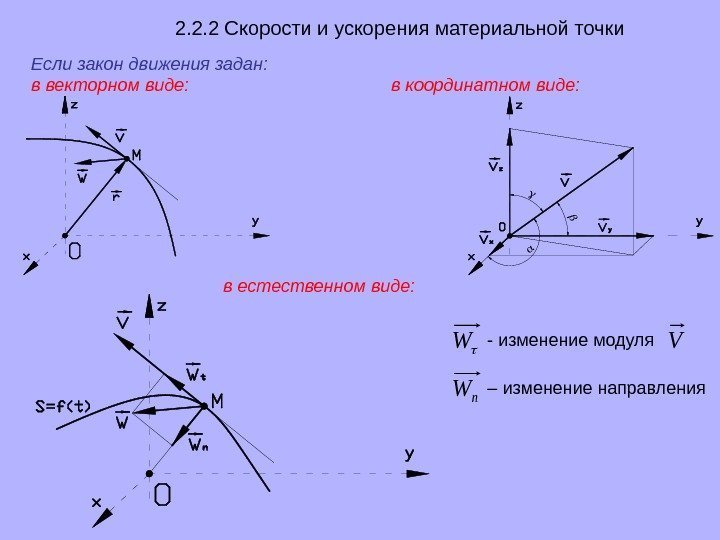
2. 2. 2 Скорости и ускорения материальной точки Если закон движения задан: в векторном виде: в координатном виде: в естественном виде: W — изменение модуля V n. W – изменение направления

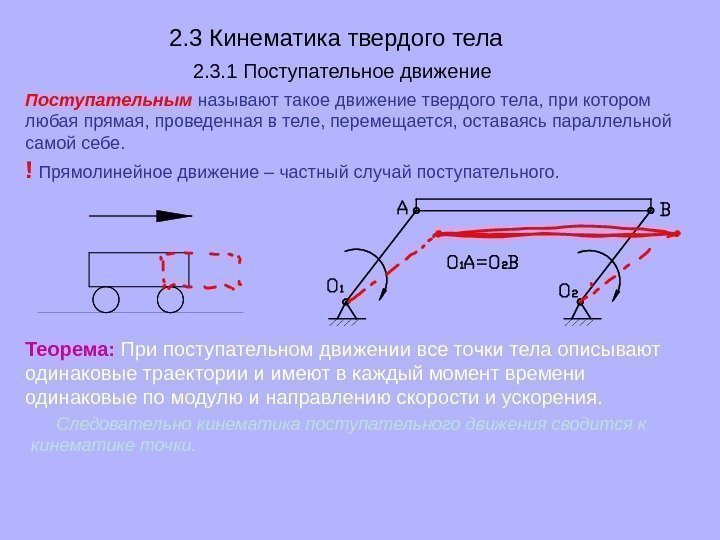
2. 3 Кинематика твердого тела 2. 3. 1 Поступательное движение Поступательным называют такое движение твердого тела, при котором любая прямая, проведенная в теле, перемещается, оставаясь параллельной самой себе. ! Прямолинейное движение – частный случай поступательного. Теорема: При поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. Следовательно кинематика поступательного движения сводится к кинематике точки.

2. 3. 2 Вращательное движение твердого тела Вращательным называется такое движение твердого тела, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во время движения неподвижными. Проходящая через эти точки прямая – ось вращения. )(tf )/1(c dt d — закон вращательного движения твердого тела — угловая скорость Вектор угловой скорости вращения в ту сторону, откуда вращение видно проходящим против хода часовой стрелки. направлен вдоль оси )/1( 2 2 2 c dt d — угловое ускорение 0 – вращение ускоренное ( одинаковый знак с ) 0 – вращение замедленное.

Равномерное и равнопеременное вращение const — вращение называют равномерным. Пусть при t = 0 0 — закон движения при равномерном вращении. , тогда 0 t Связь угловой скорости и частоты оборотов n : )/1(c)/(миноб 3060 2 nn const — вращение называют равнопеременным Пусть при t = 0 0 0 t 0 dtd dttdtd 0 — закон изменения скорости при равнопеременном вращении. 0 2 t t; ; — закон движения при равнопеременном вращении.

2. 3. 3 Скорости и ускорения точек вращающегося тела Точка М описывает окружность. dhd. S h dt d h d d. S V – линейная или окружная скорость точки М. const в заданный момент времени для всех точек тела, значит линейная скорость пропорциональна только h. Траектория т. М – окружность, радиуса h. V – касательная к этой окружности и направлена в сторону вращения. dt d. V W Ускорения т. М : 2 V Wn h , тогда h dt d h. W 2 22 h h h Wn Полное ускорение: 24224222 hhh. WWWn 2 n. W W tg

2. 3. 4 Плоскопараллельное движение твердого тела Плоскопараллельным или плоским движением твердого тела называется такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Для изучения движения всего тела достаточно изучить, как движется сечение S в плоскости x. Oy. Положение S в x. Oy полностью определяется положением в этом сечении произвольного отрезка АВ. ПР//РММ 1 Закон плоскопараллельного движения твердого тела: tf. ХА 1 tf. YА 2 tf 3 В свою очередь положение АВ полностью определяют координаты т. А ( Xa , Ya ) – полюса и угла который образует прямая АВ с осью Ох. Основные кинематические характеристики плоскопараллельного движения: поступательная компонента : вращательная компонента: АAWV, , (1)

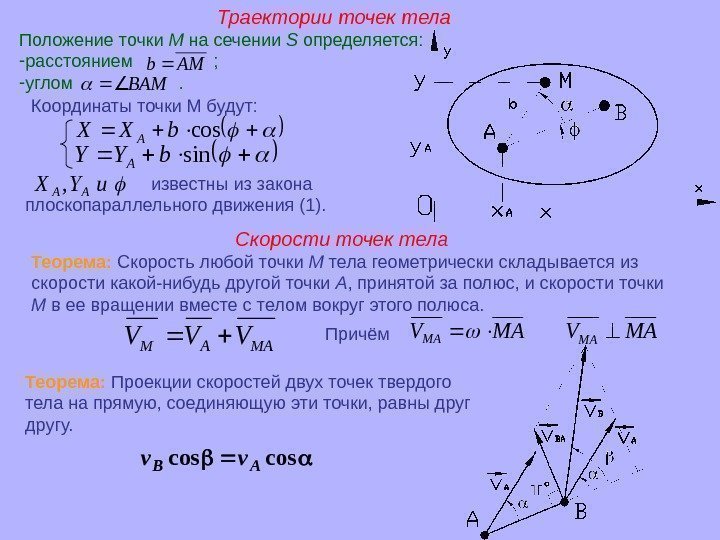
Траектории точек тела Положение точки М на сечении S определяется: — расстоянием ; — углом . AMb ВАМ Координаты точки М будут: cosb. ХXА sinb. YYА известны из закона плоскопараллельного движения (1). и. YХАA, Скорости точек тела Теорема: Скорость любой точки М тела геометрически складывается из скорости какой-нибудь другой точки А , принятой за полюс, и скорости точки М в ее вращении вместе с телом вокруг этого полюса. MAАMVVV Причём МАVMA Теорема: Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны другу. coscos. ABvv

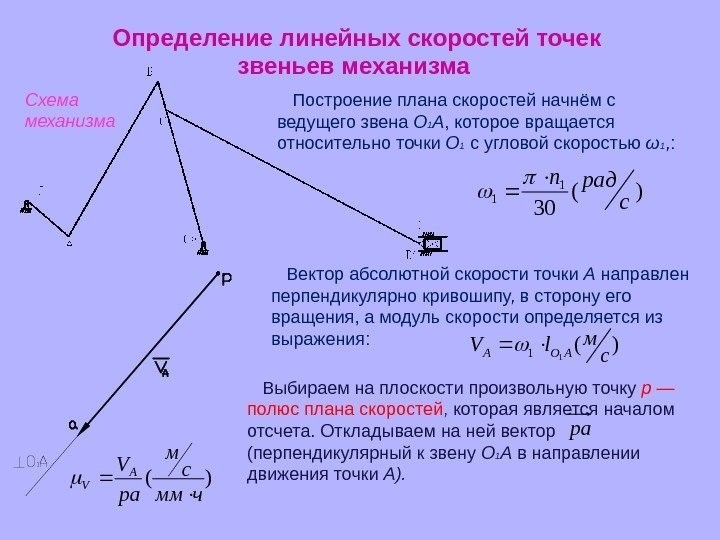
Определение линейных скоростей точек звеньев механизма Построение плана скоростей начнём с ведущего звена О 1 А , которое вращается относительно точки О 1 с угловой скоростью ω 1 , : )( 30 1 1 с радn Вектор абсолютной скорости точки А направлен перпендикулярно кривошипу, в сторону его вращения, а модуль скорости определяется из выражения: )( 11 с мl. V AOA Выбираем на плоскости произвольную точку р — полюс плана скоростей , которая является началом отсчета. Откладываем на ней вектор (перпендикулярный к звену O 1 A в направлении движения точки А). pa. Схема механизма )( чмм с м pa VA V

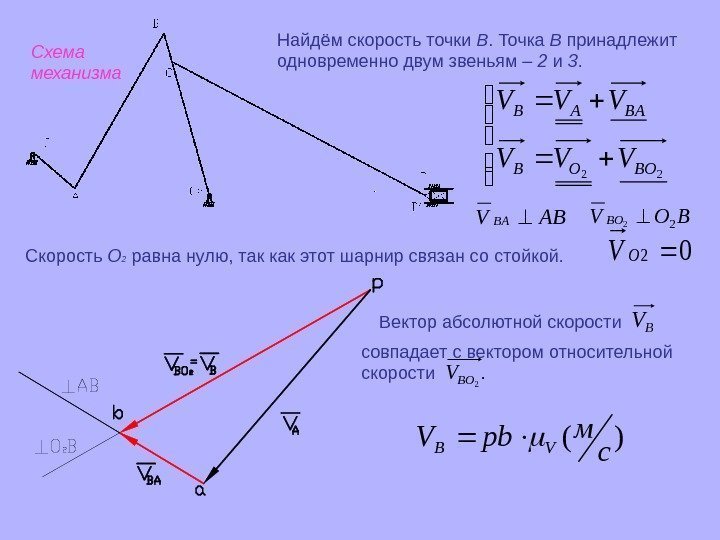
22 BООB BAAB VVVВектор абсолютной скорости BV совпадает с вектором относительной скорости . 2 B ОV )( см pb. V VB 02 OV ABVBABOVBO 22 Скорость О 2 равна нулю, так как этот шарнир связан со стойкой. Найдём скорость точки В. Точка В принадлежит одновременно двум звеньям – 2 и 3. Схема механизма

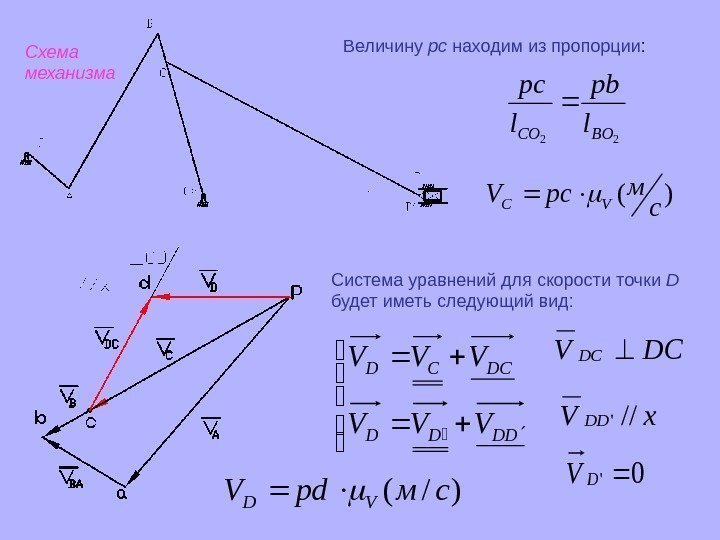
Схема механизма Величину рс находим из пропорции : 22 BOСO l рb l рс )( с мpc. VVC Система уравнений для скорости точки D будет иметь следующий вид: DDDD DCCD VVV 0’DV )/(cмpd. VVD DCVDC x. VDD//’

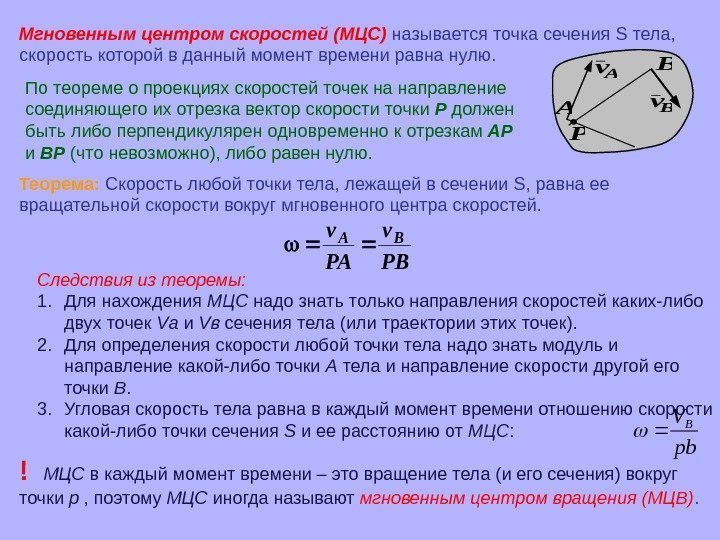
Мгновенным центром скоростей (МЦС) называется точка сечения S тела, скорость которой в данный момент времени равна нулю. A Av P B Bv По теореме о проекциях скоростей точек на направление соединяющего их отрезка вектор скорости точки Р должен быть либо перпендикулярен одновременно к отрезкам АР и ВР (что невозможно), либо равен нулю. Теорема: Скорость любой точки тела, лежащей в сечении S , равна ее вращательной скорости вокруг мгновенного центра скоростей. PB v PA v. BA Следствия из теоремы: 1. Для нахождения МЦС надо знать только направления скоростей каких-либо двух точек V а и V в сечения тела (или траектории этих точек). 2. Для определения скорости любой точки тела надо знать модуль и направление какой-либо точки А тела и направление скорости другой его точки В. 3. Угловая скорость тела равна в каждый момент времени отношению скорости какой-либо точки сечения S и ее расстоянию от МЦС : pb VB ! МЦС в каждый момент времени – это вращение тела (и его сечения) вокруг точки р , поэтому МЦС иногда называют мгновенным центром вращения (МЦВ).

Геометрическое место МЦВ на неподвижной плоскости называют неподвижной центроидой , а геометрическое место этих центров в плоскости, связанной с сечением S и движущейся вместе с ним – подвижной центроидой. Некоторые частные случаи нахождения МЦС : 1) Тело катится без скольжения по неподвижному телу 2) Если лежит под углом к АВ, то МЦС лежит в бесконечности. Точка касания тела с поверхностью Р – МЦС. BAVV//AV Значит все точки тела имеют мгновенное поступательное распределение скоростей. 3) Если , то МЦС лежит на продолжении прямой АВ. BAVV//ABVABAVV ! В механизме, состоящем из нескольких тел, каждое не поступательно движущееся тело имеет в данный момент времени свой МЦС и свою угловую скорость.

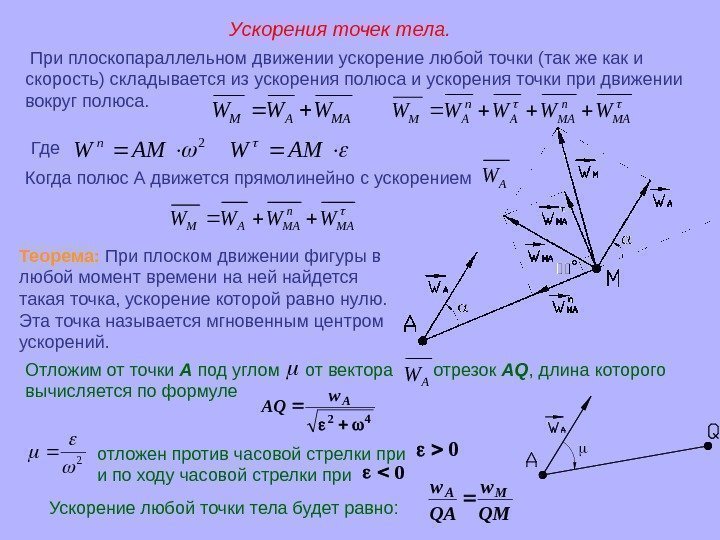
Ускорения точек тела. При плоскопараллельном движении ускорение любой точки (так же как и скорость) складывается из ускорения полюса и ускорения точки при движении вокруг полюса. MAАMWWW MA n MAA n AMWWWWW 2 AMW n AMW Где Когда полюс А движется прямолинейно с ускорением AW MA n MAAMWWWW Теорема: При плоском движении фигуры в любой момент времени на ней найдется такая точка, ускорение которой равно нулю. Эта точка называется мгно венным центром ускорений. Отложим от точки А под углом от вектора отрезок AQ , длина которого вычисляется по формуле AW 42 Aw AQ 2 отложен против часовой стрелки при и по ходу часовой стрелки при 0 0 Ускорение любой точки тела будет равно: QМ w QA w. M

Для определения направления угловой скорости второго звена ω2 необходимо мысленно перенести вектор относительной скорости из плана скоростей в точку В плана механизма, при этом видим, что вектор скорости стремится вращать точку В звена АВ относительно точки А против часовой стрелки, следовательно, и угловая скорость второго звена будет направлена против часовой стрелки. BA V Определение линейных ускорений точек звеньев механизма )/( 2 12 1 см. AOW n A и направлено вдоль кривошипа O 1 A от точки А к оси вращения О 1. Абсолютное ускорение точки А определяется только величиной нормального ускорения, которое по модулю равно: Так кривошип O 1 A вращается равномерно, то 0 11 AOW Выбираем на плоскости произвольную точку q — полюс плана ускорений , которая является началом отсчета. Откладываем на ней вектор (параллельный звену O 1 A в направлении к оси вращения O 1 ). (т. е. положительно). n AW

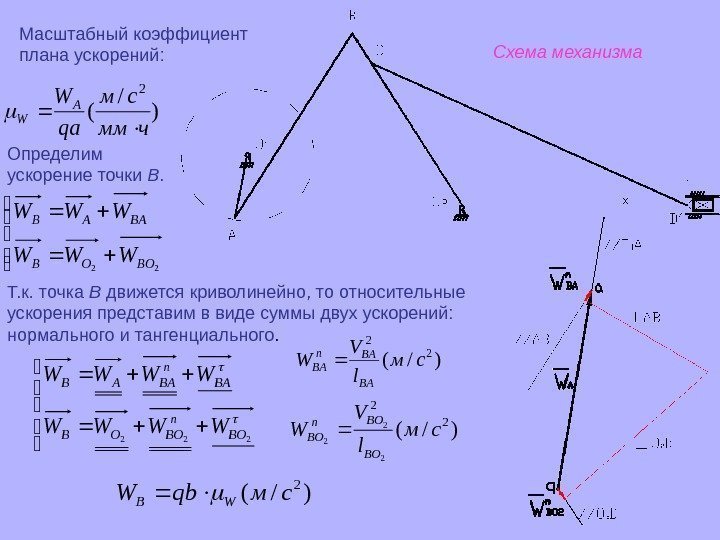
) / ( 2 чмм см qa WA W Масштабный коэффициент плана ускорений: Определим ускорение точки В. 22 BOOB BAAB WWW Схема механизма Т. к. точка В движется криволинейно, то относительные ускорения представим в виде суммы двух ускорений: нормального и тангенциального. 222 BOn BOOB BAn BAAB WWWW )/( 22 см l. V W BA BAn BA )/(2 2 2 см l V W BO BOn BO )/( 2 смqb. WW

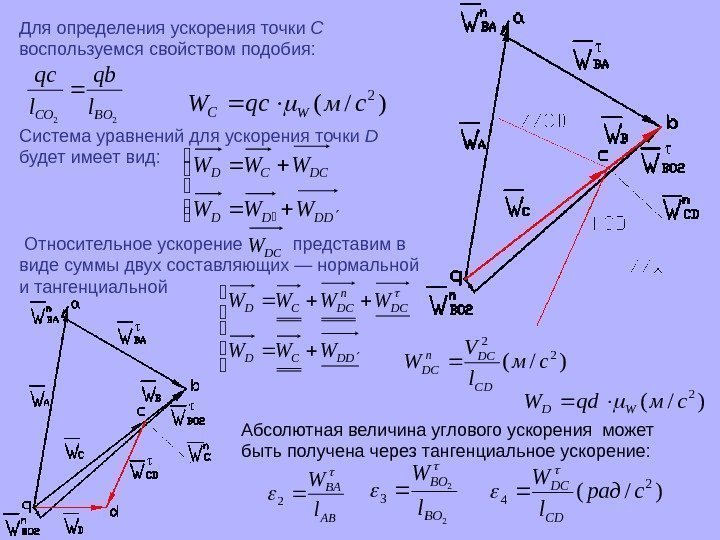
Для определения ускорения точки C воспользуемся свойством подобия: 22 BOСO l qb l q с )/( 2 смqс. WWС Система уравнений для ускорения точки D будет имеет вид: DDDD DCCD WWW Относительное ускорение представим в виде суммы двух составляющих — нормальной и тангенциальной DCW DDCD DC n DCCD WWWW )/(2 2 см l V W CD DCn DC )/(2 смqd. WWD Абсолютная величина углового ускорения может быть получена через тангенциальное ускорение: AB BA l W 2 2 23 BО BО l W )/( 2 4 срад l. W

2. 3. 5 Сложное движение точки – это движение, рассматриваемое одновременно по отношению к двум системам отсчета, когда одна считается условно неподвижной, а другая определенным образом движется по отношению к первой. Движение, совершенное точкой М по отношению к подвижным осям координат, называется относительным движением. Скорость и ускорение этого движения называют относительной скоростью и относительным ускорением ( и ). Движение, совершаемое подвижной системой отсчета со всеми точками связанного с ней пространства по отношению к неподвижной системе, является для точки М переносным движением. Скорость и ускорение этого движения называют переносной скоростью и переносным ускорением ( , )r. Vr. W e. Ve. W Абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей: rea. VVV Теорема Кориолиса: в случае непоступательного переносного движения абсолютное ускорение точки равно векторной сумме переносного, относительного и кориолисового ускорений. krea. WWWW Где sin 22 rerek. VVW — угол между векторами re. Vи