Часть 2 Использование технологии CUDA для расчета коагуляции





![Было: S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + Было: S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] +](https://present5.com/presentacii-2/20171213\39626-chasty2-raschet_koagulyacii_s_pomoschyyu_cuda.ppt\39626-chasty2-raschet_koagulyacii_s_pomoschyyu_cuda_11.jpg)

![Было: f'[iPT, i] = f[iPT, i] + dt ∙ (S+[iPT, i] – S–[iPT, i]) Было: f'[iPT, i] = f[iPT, i] + dt ∙ (S+[iPT, i] – S–[iPT, i])](https://present5.com/presentacii-2/20171213\39626-chasty2-raschet_koagulyacii_s_pomoschyyu_cuda.ppt\39626-chasty2-raschet_koagulyacii_s_pomoschyyu_cuda_13.jpg)


39626-chasty2-raschet_koagulyacii_s_pomoschyyu_cuda.ppt
- Количество слайдов: 18
 Часть 2 Использование технологии CUDA для расчета коагуляции в модели облаков Раба Н.О. аспирант кафедры информатики e-mail: [email protected]
Часть 2 Использование технологии CUDA для расчета коагуляции в модели облаков Раба Н.О. аспирант кафедры информатики e-mail: [email protected]
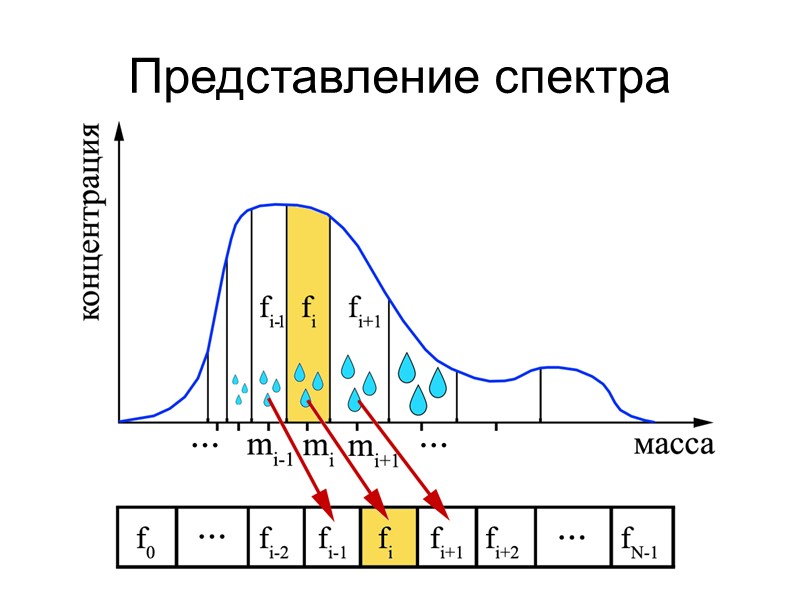
 Представление спектра
Представление спектра
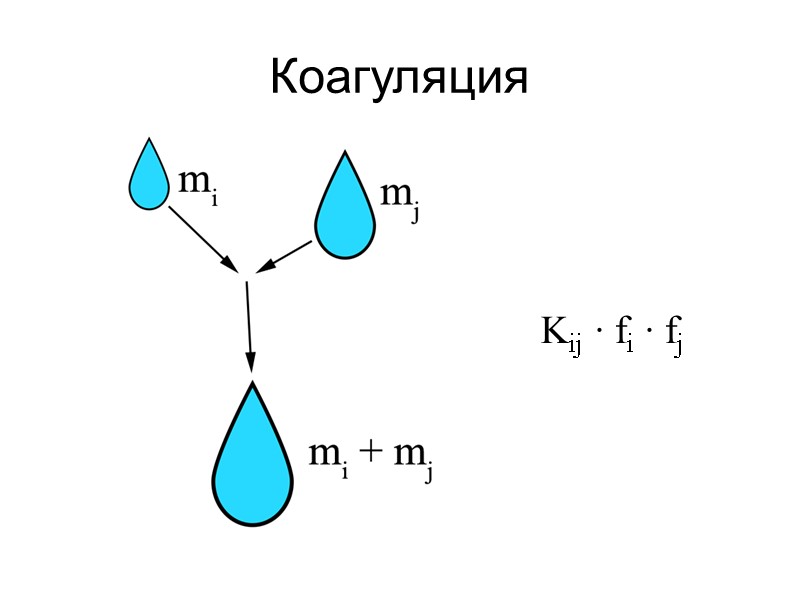
 Коагуляция Kij ∙ fi ∙ fj
Коагуляция Kij ∙ fi ∙ fj
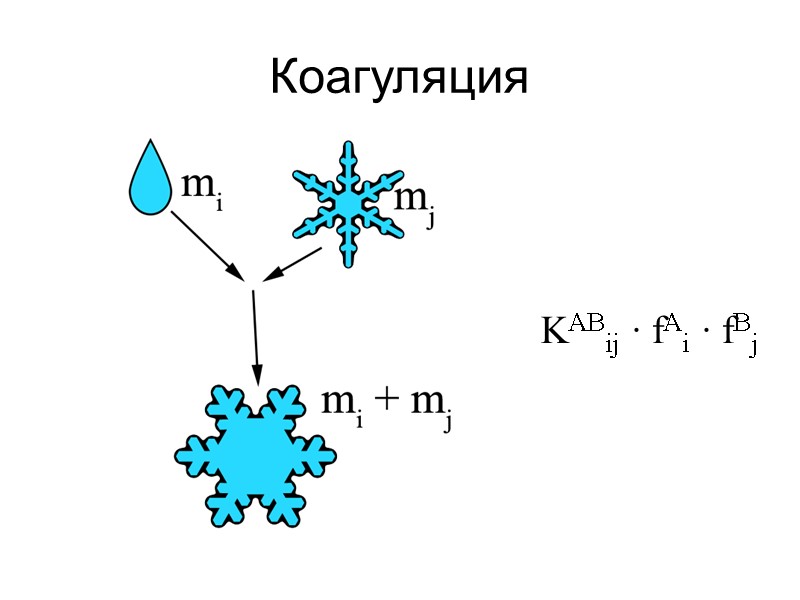
 Коагуляция KABij ∙ fAi ∙ fBj
Коагуляция KABij ∙ fAi ∙ fBj
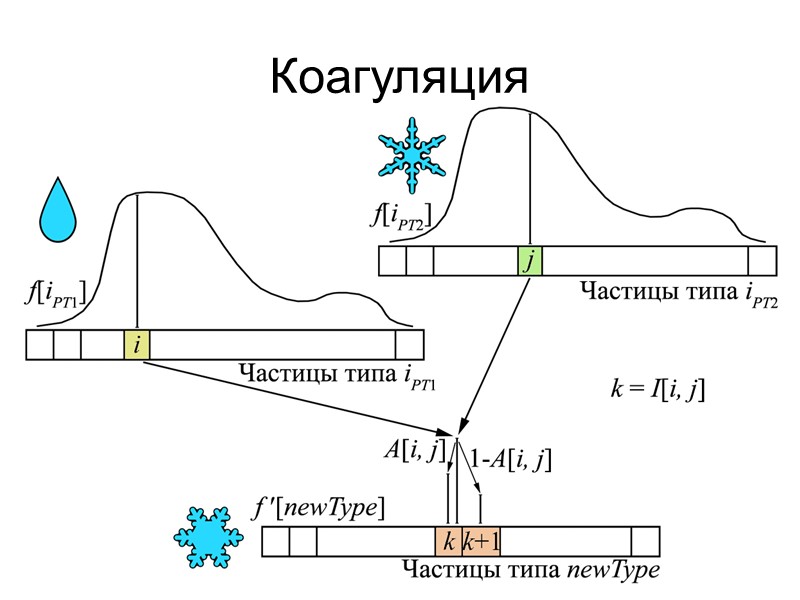
 Коагуляция
Коагуляция
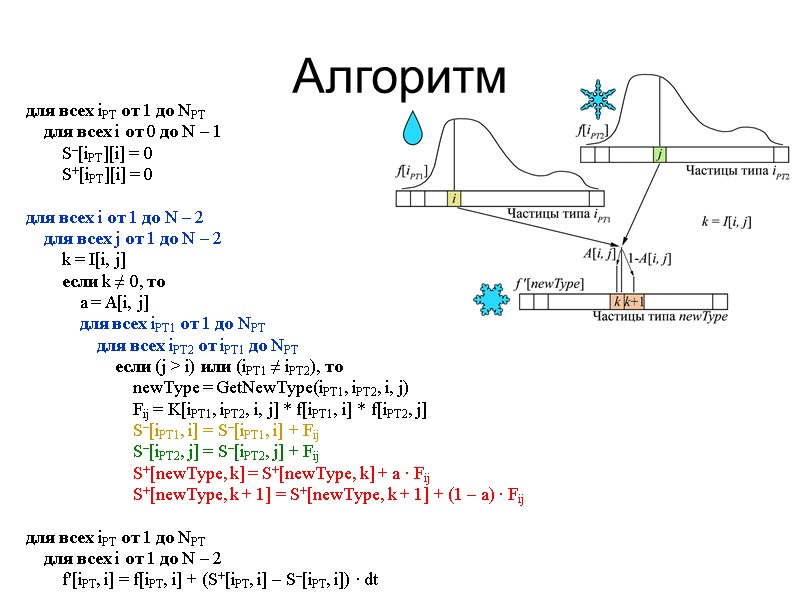
 Алгоритм для всех iPT от 1 до NPT для всех i от 0 до N – 1 S–[iPT][i] = 0 S+[iPT][i] = 0 для всех i от 1 до N – 2 для всех j от 1 до N – 2 k = I[i, j] если k ≠ 0, то a = A[i, j] для всех iPT1 от 1 до NPT для всех iPT2 от iPT1 до NPT если (j > i) или (iPT1 ≠ iPT2), то newType = GetNewType(iPT1, iPT2, i, j) Fij = K[iPT1, iPT2, i, j] * f[iPT1, i] * f[iPT2, j] S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + Fij S+[newType, k] = S+[newType, k] + a ∙ Fij S+[newType, k + 1] = S+[newType, k + 1] + (1 – a) ∙ Fij для всех iPT от 1 до NPT для всех i от 1 до N – 2 f'[iPT, i] = f[iPT, i] + (S+[iPT, i] – S–[iPT, i]) ∙ dt
Алгоритм для всех iPT от 1 до NPT для всех i от 0 до N – 1 S–[iPT][i] = 0 S+[iPT][i] = 0 для всех i от 1 до N – 2 для всех j от 1 до N – 2 k = I[i, j] если k ≠ 0, то a = A[i, j] для всех iPT1 от 1 до NPT для всех iPT2 от iPT1 до NPT если (j > i) или (iPT1 ≠ iPT2), то newType = GetNewType(iPT1, iPT2, i, j) Fij = K[iPT1, iPT2, i, j] * f[iPT1, i] * f[iPT2, j] S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + Fij S+[newType, k] = S+[newType, k] + a ∙ Fij S+[newType, k + 1] = S+[newType, k + 1] + (1 – a) ∙ Fij для всех iPT от 1 до NPT для всех i от 1 до N – 2 f'[iPT, i] = f[iPT, i] + (S+[iPT, i] – S–[iPT, i]) ∙ dt
 Способ распараллеливания Каждый поток обрабатывает столкновение частицы типа iPT1 из интервала i с частицами разных типов (iPT2 ≥ iPT1) из интервала j (внутренний цикл) iPT1, i и j определяются индексом потока
Способ распараллеливания Каждый поток обрабатывает столкновение частицы типа iPT1 из интервала i с частицами разных типов (iPT2 ≥ iPT1) из интервала j (внутренний цикл) iPT1, i и j определяются индексом потока
 Способ распараллеливания для всех i от 1 до N – 2 для всех j от 1 до N – 2 k = I[i, j] если k ≠ 0, то a = A[i, j] для всех iPT1 от 1 до NPT для всех iPT2 от iPT1 до NPT если (j > i) или (iPT1 ≠ iPT2), то newType = GetNewType(iPT1, iPT2, i, j) Fij = K[iPT1, iPT2, i, j] * f[iPT1, i] * f[iPT2, j] S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + Fij S+[newType, k] = S+[newType, k] + a ∙ Fij S+[newType, k + 1] = S+[newType, k + 1] + (1 – a) ∙ Fij
Способ распараллеливания для всех i от 1 до N – 2 для всех j от 1 до N – 2 k = I[i, j] если k ≠ 0, то a = A[i, j] для всех iPT1 от 1 до NPT для всех iPT2 от iPT1 до NPT если (j > i) или (iPT1 ≠ iPT2), то newType = GetNewType(iPT1, iPT2, i, j) Fij = K[iPT1, iPT2, i, j] * f[iPT1, i] * f[iPT2, j] S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + Fij S+[newType, k] = S+[newType, k] + a ∙ Fij S+[newType, k + 1] = S+[newType, k + 1] + (1 – a) ∙ Fij
 Ядро (вариант 1) t = blockDim.y ∙ blockIdx.y + threadIdx.y iPT1 = t / N i = t % N j = blockDim.x ∙ blockIdx.x + threadIdx.x если (i < N - 1) и (j < N - 1) и (i > 0) и (j > 0), то k = I[i, j] если k ≠ 0, то a = A[i, j] для всех iPT2 от iPT1 до NPT если (j > i) или (iPT1 ≠ iPT2), то newType = GetNewType(iPT1, iPT2, i, j) Fij = K[iPT1, iPT2, i, j] * f[iPT1, i] * f[iPT2, j] S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + Fij S+[newType, k] = S+[newType, k] + a ∙ Fij S+[newType, k + 1] = S+[newType, k + 1] + (1 – a) ∙ Fij
Ядро (вариант 1) t = blockDim.y ∙ blockIdx.y + threadIdx.y iPT1 = t / N i = t % N j = blockDim.x ∙ blockIdx.x + threadIdx.x если (i < N - 1) и (j < N - 1) и (i > 0) и (j > 0), то k = I[i, j] если k ≠ 0, то a = A[i, j] для всех iPT2 от iPT1 до NPT если (j > i) или (iPT1 ≠ iPT2), то newType = GetNewType(iPT1, iPT2, i, j) Fij = K[iPT1, iPT2, i, j] * f[iPT1, i] * f[iPT2, j] S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + Fij S+[newType, k] = S+[newType, k] + a ∙ Fij S+[newType, k + 1] = S+[newType, k + 1] + (1 – a) ∙ Fij
 Дополнительные массивы и индексы “Развернутый” массив MP Индексы ind Индексы pos
Дополнительные массивы и индексы “Развернутый” массив MP Индексы ind Индексы pos
![>Было: S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + >Было: S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] +](https://present5.com/presentacii-2/20171213\39626-chasty2-raschet_koagulyacii_s_pomoschyyu_cuda.ppt\39626-chasty2-raschet_koagulyacii_s_pomoschyyu_cuda_11.jpg) Было: S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + Fij S+[newType, k] = S+[newType, k] + a ∙ Fij S+[newType, k + 1] = S+[newType, k + 1] + (1 – a) ∙ Fij Стало: MP[ind[0, iPT1, iPT2, i, j]] = Fij MP[ind[1, iPT1, iPT2, i, j]] = Fij MP[ind[2, iPT1, iPT2, i, j]] = a ∙ Fij MP[ind[3, iPT1, iPT2, i, j]] = (1 – a) ∙ Fij
Было: S–[iPT1, i] = S–[iPT1, i] + Fij S–[iPT2, j] = S–[iPT2, j] + Fij S+[newType, k] = S+[newType, k] + a ∙ Fij S+[newType, k + 1] = S+[newType, k + 1] + (1 – a) ∙ Fij Стало: MP[ind[0, iPT1, iPT2, i, j]] = Fij MP[ind[1, iPT1, iPT2, i, j]] = Fij MP[ind[2, iPT1, iPT2, i, j]] = a ∙ Fij MP[ind[3, iPT1, iPT2, i, j]] = (1 – a) ∙ Fij
 Ядро (вариант 2) t = blockDim.y ∙ blockIdx.y + threadIdx.y iPT1 = t / N i = t % N j = blockDim.x ∙ blockIdx.x + threadIdx.x если (i < N - 1) и (j < N - 1) и (i > 0) и (j > 0), то k = I[i, j] если k ≠ 0, то a = A[i, j] для всех iPT2 от iPT1 до NPT если (j > i) или (iPT1 ≠ iPT2), то newType = GetNewType(iPT1, iPT2, i, j) Fij = K[iPT1, iPT2, i, j] * f[iPT1, i] * f[iPT2, j] MP[ind[0, iPT1, iPT2, i, j]] = Fij MP[ind[1, iPT1, iPT2, i, j]] = Fij MP[ind[2, iPT1, iPT2, i, j]] = a ∙ Fij MP[ind[3, iPT1, iPT2, i, j]] = (1 – a) ∙ Fij
Ядро (вариант 2) t = blockDim.y ∙ blockIdx.y + threadIdx.y iPT1 = t / N i = t % N j = blockDim.x ∙ blockIdx.x + threadIdx.x если (i < N - 1) и (j < N - 1) и (i > 0) и (j > 0), то k = I[i, j] если k ≠ 0, то a = A[i, j] для всех iPT2 от iPT1 до NPT если (j > i) или (iPT1 ≠ iPT2), то newType = GetNewType(iPT1, iPT2, i, j) Fij = K[iPT1, iPT2, i, j] * f[iPT1, i] * f[iPT2, j] MP[ind[0, iPT1, iPT2, i, j]] = Fij MP[ind[1, iPT1, iPT2, i, j]] = Fij MP[ind[2, iPT1, iPT2, i, j]] = a ∙ Fij MP[ind[3, iPT1, iPT2, i, j]] = (1 – a) ∙ Fij
![>Было: f'[iPT, i] = f[iPT, i] + dt ∙ (S+[iPT, i] – S–[iPT, i]) >Было: f'[iPT, i] = f[iPT, i] + dt ∙ (S+[iPT, i] – S–[iPT, i])](https://present5.com/presentacii-2/20171213\39626-chasty2-raschet_koagulyacii_s_pomoschyyu_cuda.ppt\39626-chasty2-raschet_koagulyacii_s_pomoschyyu_cuda_13.jpg) Было: f'[iPT, i] = f[iPT, i] + dt ∙ (S+[iPT, i] – S–[iPT, i]) Стало: f'[iPT, i] = f[iPT, i] + dt ∙ (MP[pos[1, iPT, i – 1] + 1] + MP[pos[1, iPT, i – 1] + 2] + … + MP[pos[1, iPT, i]] – MP[pos[0, iPT, i – 1] + 1] – MP[pos[0, iPT, i – 1] + 2] – … – MP[pos[0, iPT, i]])
Было: f'[iPT, i] = f[iPT, i] + dt ∙ (S+[iPT, i] – S–[iPT, i]) Стало: f'[iPT, i] = f[iPT, i] + dt ∙ (MP[pos[1, iPT, i – 1] + 1] + MP[pos[1, iPT, i – 1] + 2] + … + MP[pos[1, iPT, i]] – MP[pos[0, iPT, i – 1] + 1] – MP[pos[0, iPT, i – 1] + 2] – … – MP[pos[0, iPT, i]])
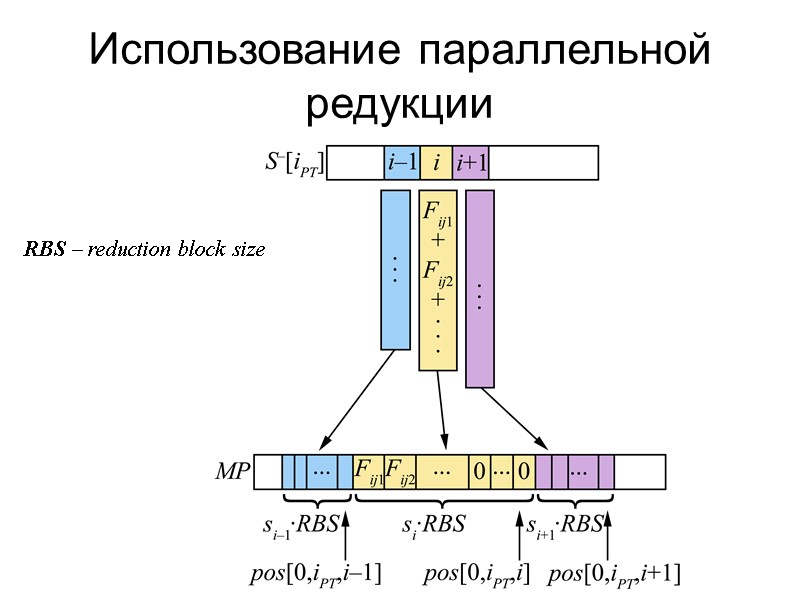
 Использование параллельной редукции RBS – reduction block size
Использование параллельной редукции RBS – reduction block size
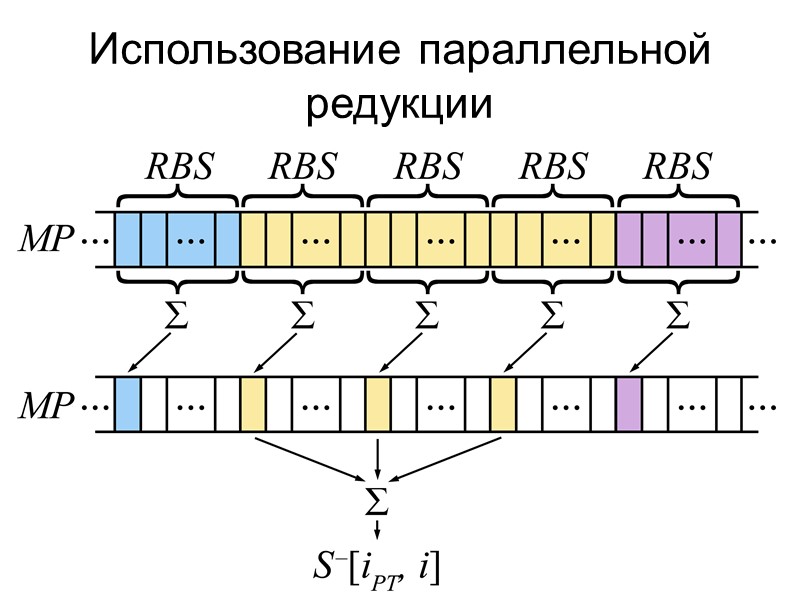
 Использование параллельной редукции
Использование параллельной редукции
 Принцип работы Инициализация Расчет I, A, ind, pos (на CPU) Загрузка в память видеокарты K, I, A, ind, pos Выделение памяти видеокарты под f, f’, MP, S–, S+
Принцип работы Инициализация Расчет I, A, ind, pos (на CPU) Загрузка в память видеокарты K, I, A, ind, pos Выделение памяти видеокарты под f, f’, MP, S–, S+
 Принцип работы Шаг вычисления коагуляции Загрузка f в память видеокарты Обнуление MP (kernel 1) Заполнение MP (kernel 2) Вычисление суммы по областям MP длиной RBS (параллельная редукция) (kernel 3) Суммирование частей MP, вычисление S– и S+ (kernel 4) Вычисление f’ (kernel 5) Копирование f’ в основную память
Принцип работы Шаг вычисления коагуляции Загрузка f в память видеокарты Обнуление MP (kernel 1) Заполнение MP (kernel 2) Вычисление суммы по областям MP длиной RBS (параллельная редукция) (kernel 3) Суммирование частей MP, вычисление S– и S+ (kernel 4) Вычисление f’ (kernel 5) Копирование f’ в основную память
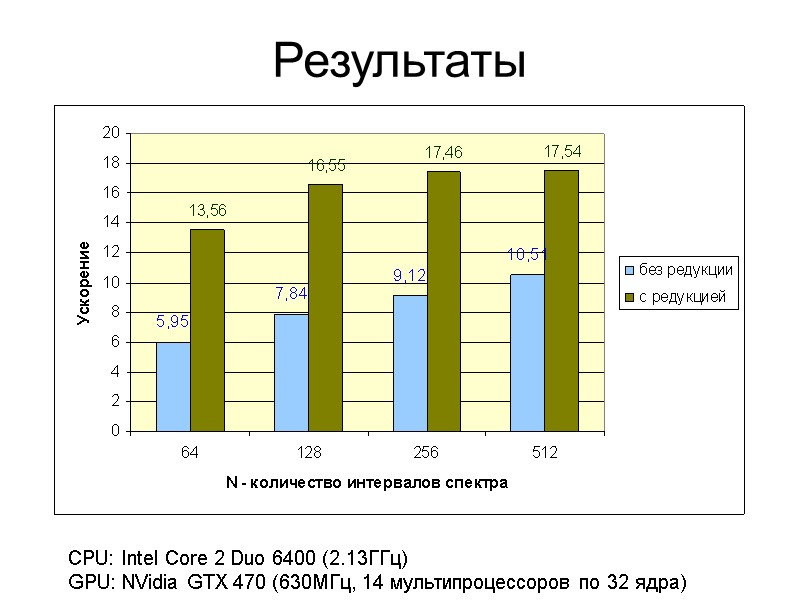
 Результаты CPU: Intel Core 2 Duo 6400 (2.13ГГц) GPU: NVidia GTX 470 (630МГц, 14 мультипроцессоров по 32 ядра)
Результаты CPU: Intel Core 2 Duo 6400 (2.13ГГц) GPU: NVidia GTX 470 (630МГц, 14 мультипроцессоров по 32 ядра)
