Цель урока: изучить второй признак равенства треугольников; научиться


№_13.__vtoroy_priznak_ravenstva_treugolynikov.ppt
- Размер: 1.1 Мб
- Автор:
- Количество слайдов: 26
Описание презентации Цель урока: изучить второй признак равенства треугольников; научиться по слайдам
 Цель урока: изучить второй признак равенства треугольников; научиться применять его при решении задач.
Цель урока: изучить второй признак равенства треугольников; научиться применять его при решении задач.
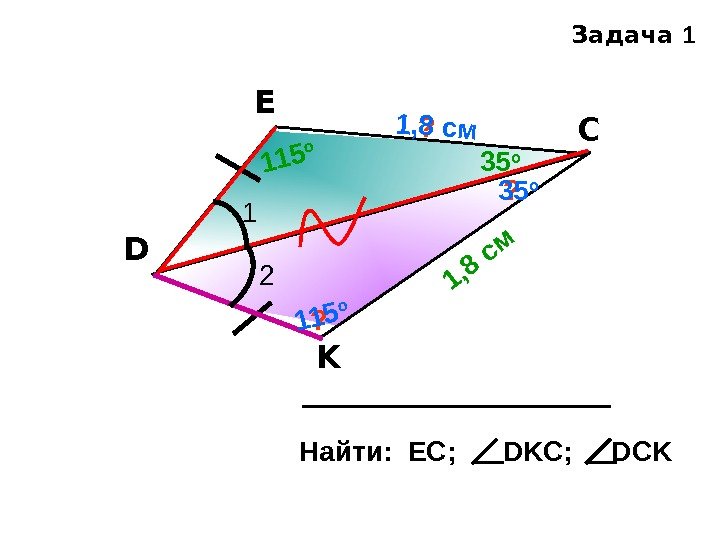
 D E С K Найти: EC; DKC; DCK Задача 1 1 21, 8 см 35 о 115 о? ? ? 1, 8 см 35 о 115 о
D E С K Найти: EC; DKC; DCK Задача 1 1 21, 8 см 35 о 115 о? ? ? 1, 8 см 35 о 115 о
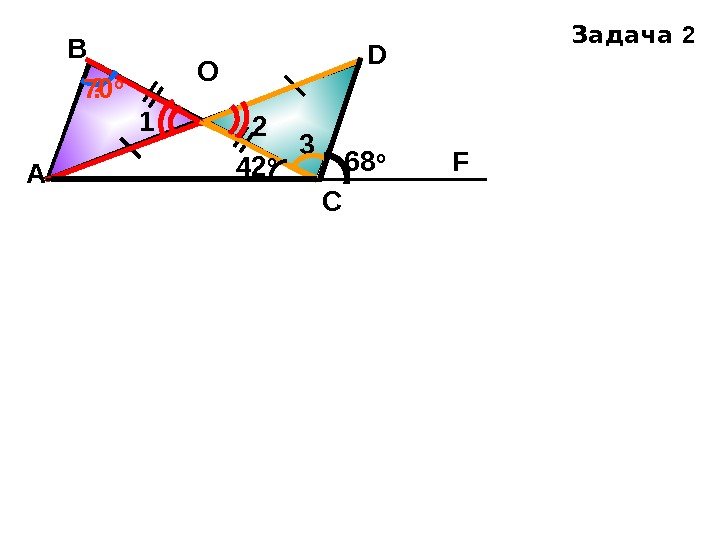
 А D СВ О ? 1 2 3 F 42 o 68 o 70 o Задача
А D СВ О ? 1 2 3 F 42 o 68 o 70 o Задача
 Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Второй признак равенства треугольников У С Л О В И Е З А К Л Ю Ч Е Н И Е
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Второй признак равенства треугольников У С Л О В И Е З А К Л Ю Ч Е Н И Е
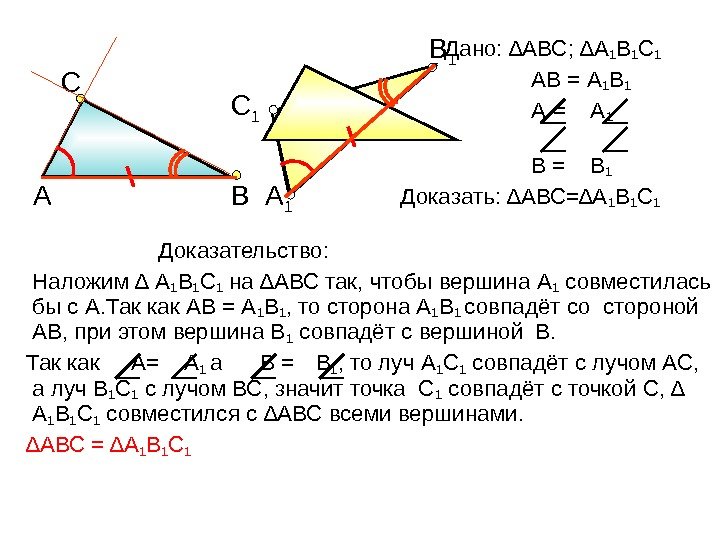
 Дано: ∆АВС; ∆А 1 В 1 С 1 АВ = А 1 В 1 А = А 1 В = В 1 Доказать: ∆АВС=∆А 1 В 1 С 1 Доказательство: Наложим ∆ А 1 В 1 С 1 на ∆АВС так, чтобы вершина А 1 совместилась бы с А. Так как АВ = А 1 В 1 , то сторона А 1 В 1 совпадёт со стороной АВ, при этом вершина В 1 совпадёт с вершиной В. Так как А= А 1 а В = В 1 , то луч А 1 С 1 совпадёт с лучом АС, а луч В 1 С 1 с лучом ВС, значит точка С 1 совпадёт с точкой С, ∆ А 1 В 1 С 1 совместился с ∆АВС всеми вершинами. ∆ АВС = ∆А 1 В 1 С 1 А ВС А 1 В 1 С
Дано: ∆АВС; ∆А 1 В 1 С 1 АВ = А 1 В 1 А = А 1 В = В 1 Доказать: ∆АВС=∆А 1 В 1 С 1 Доказательство: Наложим ∆ А 1 В 1 С 1 на ∆АВС так, чтобы вершина А 1 совместилась бы с А. Так как АВ = А 1 В 1 , то сторона А 1 В 1 совпадёт со стороной АВ, при этом вершина В 1 совпадёт с вершиной В. Так как А= А 1 а В = В 1 , то луч А 1 С 1 совпадёт с лучом АС, а луч В 1 С 1 с лучом ВС, значит точка С 1 совпадёт с точкой С, ∆ А 1 В 1 С 1 совместился с ∆АВС всеми вершинами. ∆ АВС = ∆А 1 В 1 С 1 А ВС А 1 В 1 С
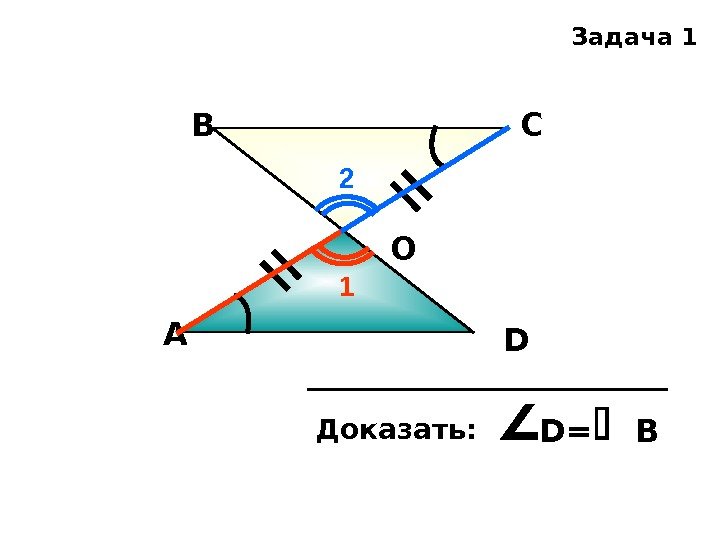
 А В С DО Доказать: D = ВЗадача
А В С DО Доказать: D = ВЗадача
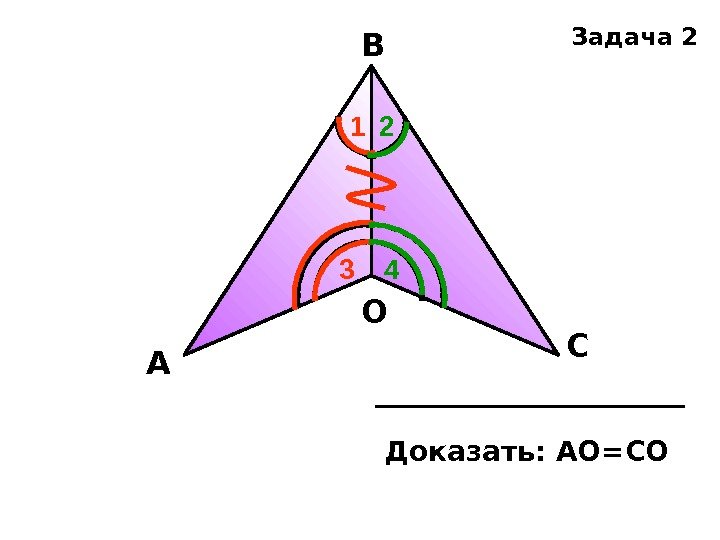
 А В СО Доказать: АО=СО Задача
А В СО Доказать: АО=СО Задача
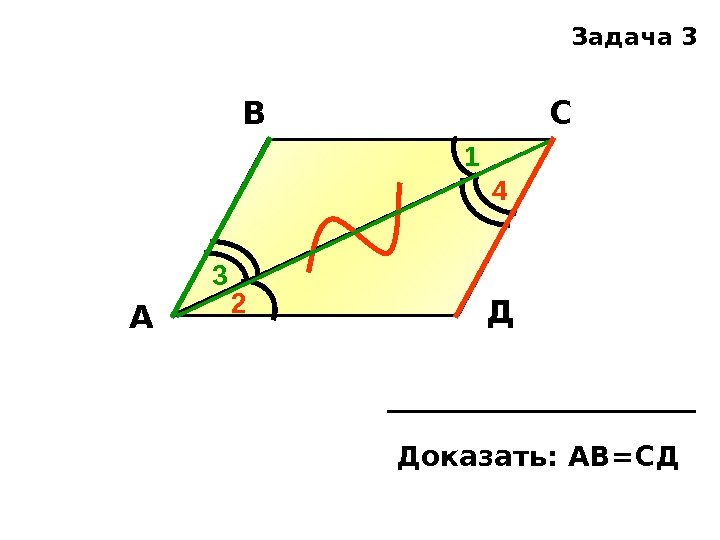
 А Д СВ Доказать: АВ=СД Задача
А Д СВ Доказать: АВ=СД Задача
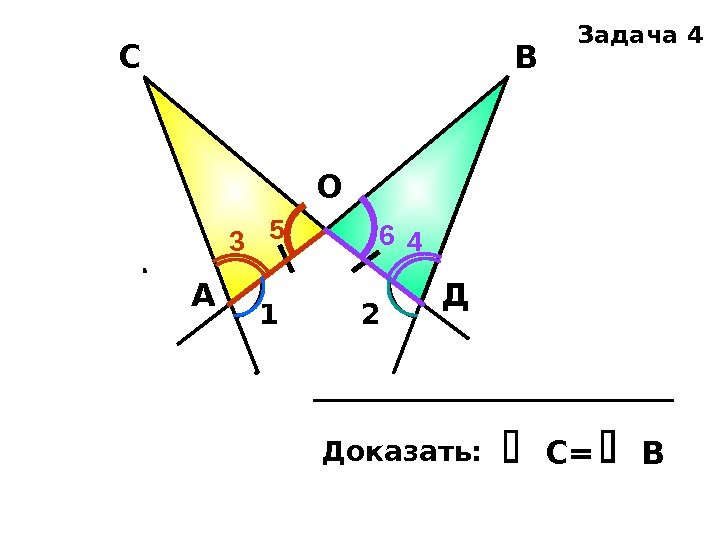
 Доказать: С= ВАС В ДО 1 2 Задача
Доказать: С= ВАС В ДО 1 2 Задача
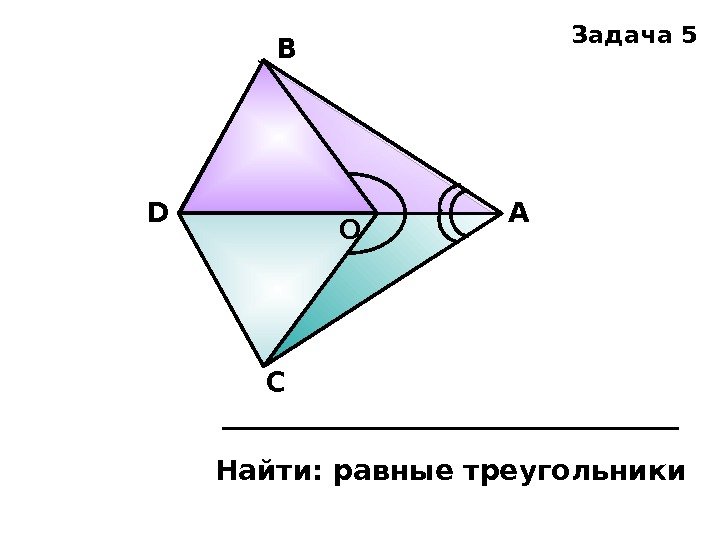
 АВ СD Найти: равные треугольники О Задача 5 O
АВ СD Найти: равные треугольники О Задача 5 O
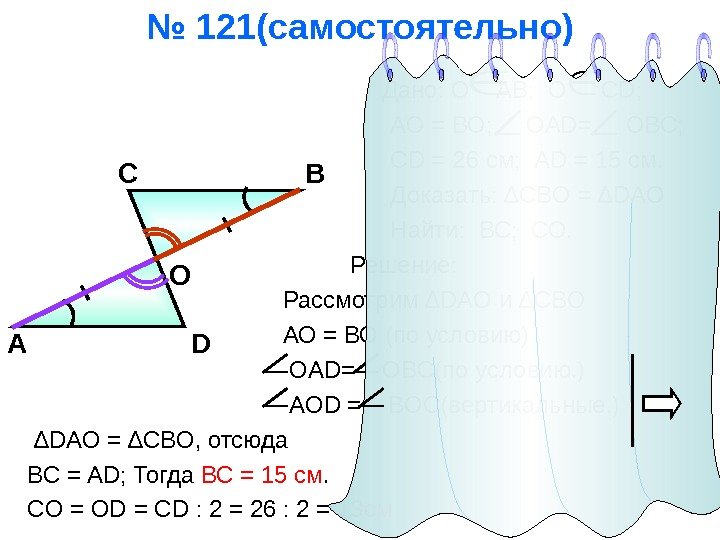
 № 121(самостоятельно) Дано: О АВ; О CD ; АО = ВО; OAD= OBC ; CD = 26 c м; AD = 15 см. Доказать: ∆ CBO = ∆ DAO Найти: ВС; СО. Решение: Рассмотрим ∆ DAO и ∆ CBO АО = ВО (по условию) OAD= OBC (по условию. ) АО D = BOC( вертикальные. ) ∆ DAO = ∆ CBO , отсюда BC = AD; Тогда ВС = 15 см. CO = OD = CD : 2 = 26 : 2 = 13 см А В О DС
№ 121(самостоятельно) Дано: О АВ; О CD ; АО = ВО; OAD= OBC ; CD = 26 c м; AD = 15 см. Доказать: ∆ CBO = ∆ DAO Найти: ВС; СО. Решение: Рассмотрим ∆ DAO и ∆ CBO АО = ВО (по условию) OAD= OBC (по условию. ) АО D = BOC( вертикальные. ) ∆ DAO = ∆ CBO , отсюда BC = AD; Тогда ВС = 15 см. CO = OD = CD : 2 = 26 : 2 = 13 см А В О DС
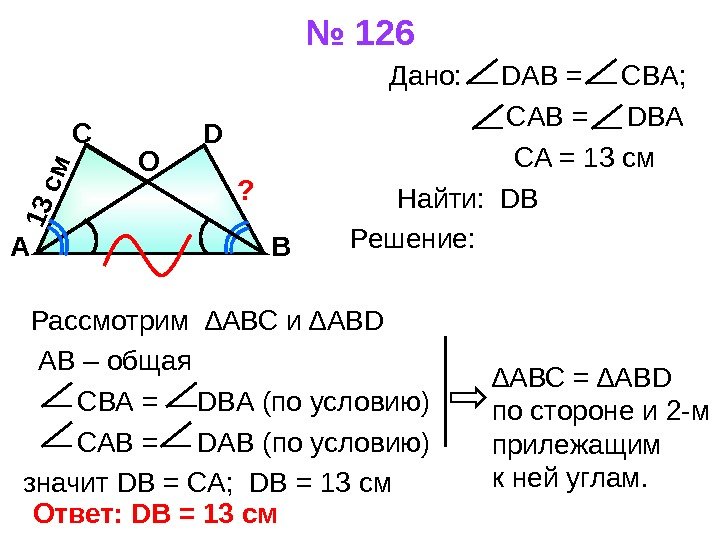
 № 126 Дано: DAB = CBA; CAB = DBA CA = 13 см Найти: DB Решение: Рассмотрим ∆АВС и ∆А BD АВ – общая СВА = DBA (по условию) САВ = D АВ (по условию) значит DB = CA ; D В = 13 см. А ВС D О 1 3 с м ? ∆ АВС = ∆АВ D по стороне и 2 — м прилежащим к ней углам. Ответ: D В = 13 см
№ 126 Дано: DAB = CBA; CAB = DBA CA = 13 см Найти: DB Решение: Рассмотрим ∆АВС и ∆А BD АВ – общая СВА = DBA (по условию) САВ = D АВ (по условию) значит DB = CA ; D В = 13 см. А ВС D О 1 3 с м ? ∆ АВС = ∆АВ D по стороне и 2 — м прилежащим к ней углам. Ответ: D В = 13 см
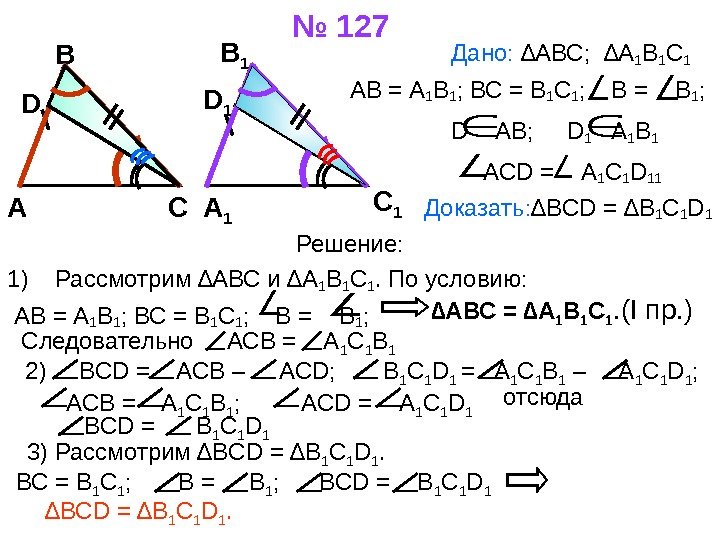
 № 127 Дано: ∆АВС; ∆А 1 В 1 С 1 АВ = А 1 В 1 ; ВС = В 1 С 1 ; В = В 1 ; D AB; D 1 A 1 B 1 ACD = A 1 C 1 D 11 Доказать: ∆ BCD = ∆ B 1 C 1 D 1 Решение: 1) Рассмотрим ∆АВС и ∆А 1 В 1 С 1. По условию: АВ = А 1 В 1 ; ВС = В 1 С 1 ; В = В 1 ; А В С А 1 В 1 С 1 D 1 D ∆ АВС = ∆А 1 В 1 С 1. ( I пр. ) Следовательно АСВ = А 1 С 1 В 1 2) BCD = ACB – ACD; B 1 C 1 D 1 = A 1 C 1 B 1 – A 1 C 1 D 1 ; ACB = A 1 C 1 B 1 ; ACD = A 1 C 1 D 1 BCD = B 1 C 1 D 1 отсюда 3) Рассмотрим ∆ BCD = ∆ B 1 C 1 D 1. ВС = В 1 С 1 ; В = В 1 ; BCD = B 1 C 1 D 1 ∆ BCD = ∆ B 1 C 1 D 1.
№ 127 Дано: ∆АВС; ∆А 1 В 1 С 1 АВ = А 1 В 1 ; ВС = В 1 С 1 ; В = В 1 ; D AB; D 1 A 1 B 1 ACD = A 1 C 1 D 11 Доказать: ∆ BCD = ∆ B 1 C 1 D 1 Решение: 1) Рассмотрим ∆АВС и ∆А 1 В 1 С 1. По условию: АВ = А 1 В 1 ; ВС = В 1 С 1 ; В = В 1 ; А В С А 1 В 1 С 1 D 1 D ∆ АВС = ∆А 1 В 1 С 1. ( I пр. ) Следовательно АСВ = А 1 С 1 В 1 2) BCD = ACB – ACD; B 1 C 1 D 1 = A 1 C 1 B 1 – A 1 C 1 D 1 ; ACB = A 1 C 1 B 1 ; ACD = A 1 C 1 D 1 BCD = B 1 C 1 D 1 отсюда 3) Рассмотрим ∆ BCD = ∆ B 1 C 1 D 1. ВС = В 1 С 1 ; В = В 1 ; BCD = B 1 C 1 D 1 ∆ BCD = ∆ B 1 C 1 D 1.
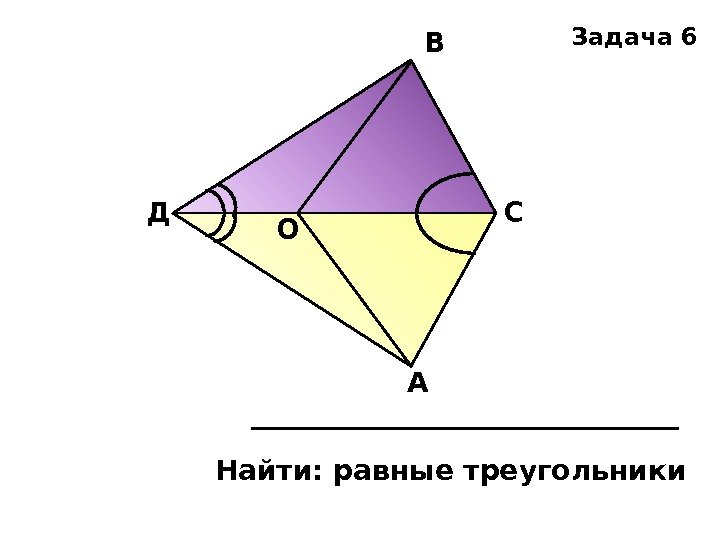
 Д О В С А Найти: равные треугольники Задача
Д О В С А Найти: равные треугольники Задача
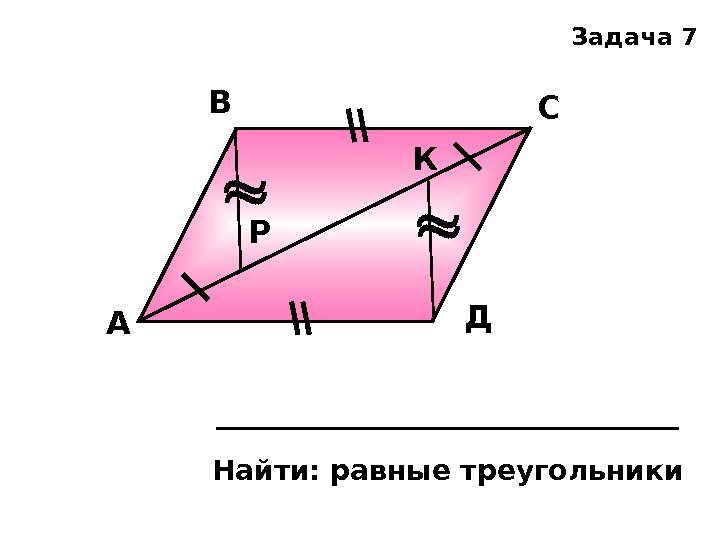
 А В С ДК Р Найти: равные треугольники Задача
А В С ДК Р Найти: равные треугольники Задача
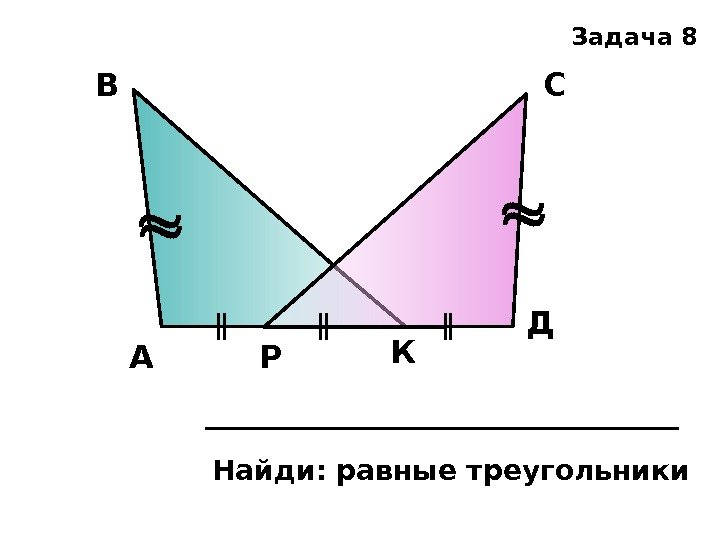
 АВ С Д Р К Найди: равные треугольники Задача
АВ С Д Р К Найди: равные треугольники Задача
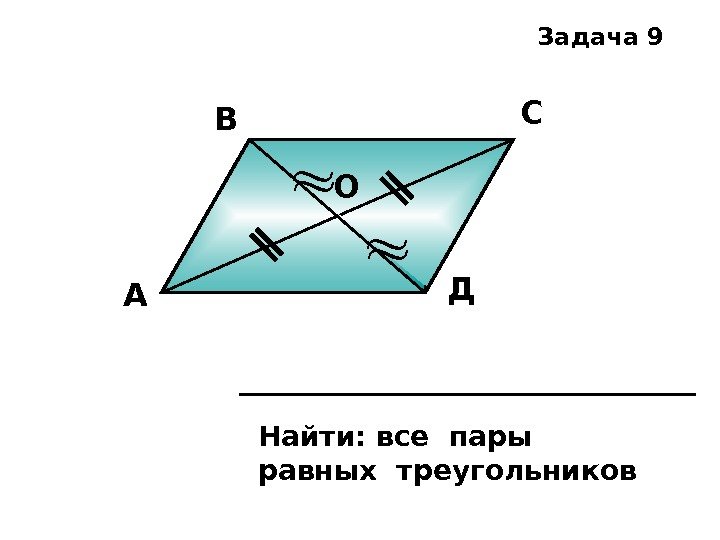
 А В С ДО Найти: все пары равных треугольников Задача
А В С ДО Найти: все пары равных треугольников Задача
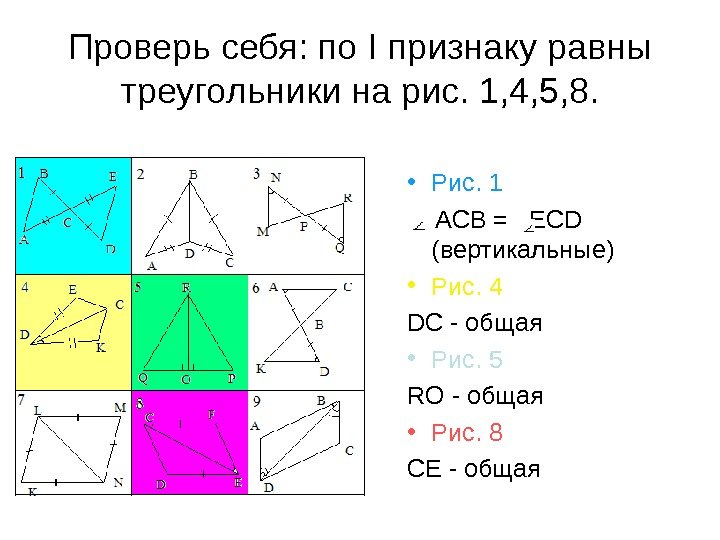
 Проверь себя: по I признаку равны треугольники на рис. 1, 4, 5, 8. • Рис. 1 ACB = ECD ( вертикальные) • Рис. 4 DC — общая • Рис. 5 RO — общая • Рис. 8 CE — общая
Проверь себя: по I признаку равны треугольники на рис. 1, 4, 5, 8. • Рис. 1 ACB = ECD ( вертикальные) • Рис. 4 DC — общая • Рис. 5 RO — общая • Рис. 8 CE — общая
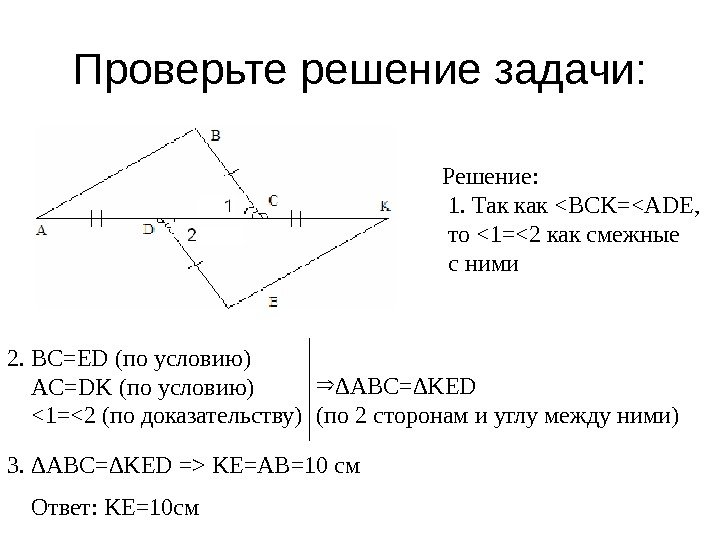
 Проверьте решение задачи: Решение: 1. Так как <BCK=<ADE, то <1=<2 как смежные с ними 2. BC=ED ( по условию) AC=DK ( по условию) <1= KE=AB=10 см Ответ: KE=10 см
Проверьте решение задачи: Решение: 1. Так как <BCK=<ADE, то <1=<2 как смежные с ними 2. BC=ED ( по условию) AC=DK ( по условию) <1= KE=AB=10 см Ответ: KE=10 см
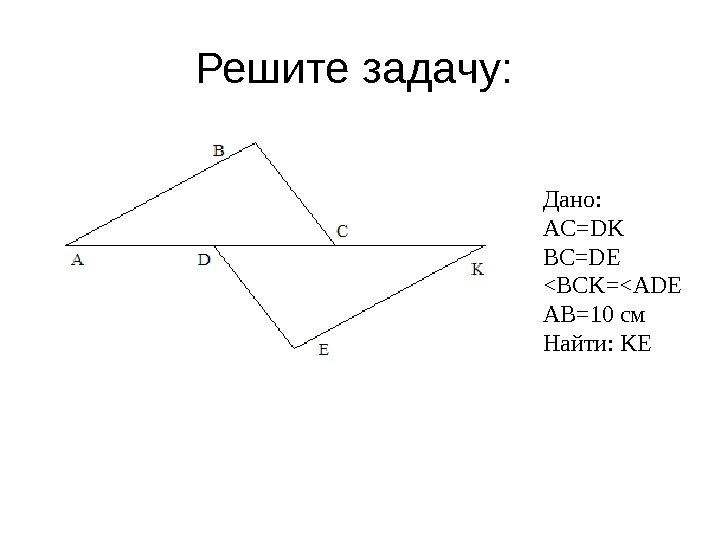
 Решите задачу: Дано: AC=DK BC=DE <BCK=<ADE AB=10 см Найти: K
Решите задачу: Дано: AC=DK BC=DE <BCK=<ADE AB=10 см Найти: K
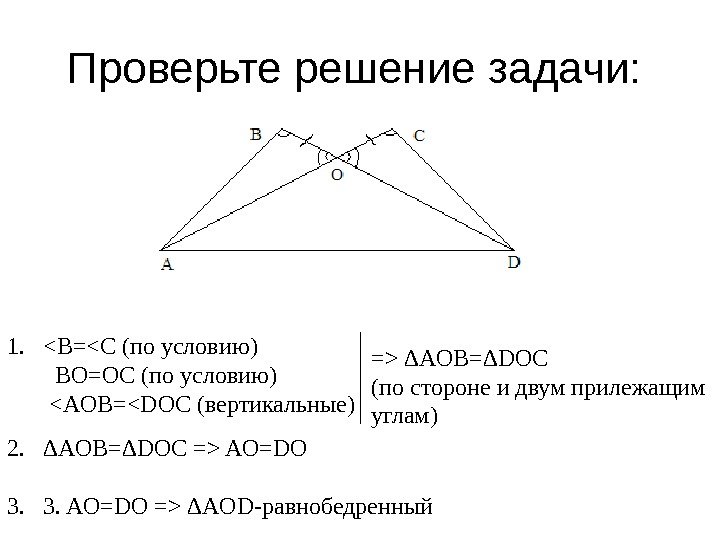
 Проверьте решение задачи: 1. <B=<C (по условию) BO=OC (по условию) <AOB= ∆AOB=∆DOC ( по стороне и двум прилежащим углам) 2. ∆ AOB= ∆ DOC => AO=DO 3. 3. AO=DO => ∆AOD- равнобедренный
Проверьте решение задачи: 1. <B=<C (по условию) BO=OC (по условию) <AOB= ∆AOB=∆DOC ( по стороне и двум прилежащим углам) 2. ∆ AOB= ∆ DOC => AO=DO 3. 3. AO=DO => ∆AOD- равнобедренный
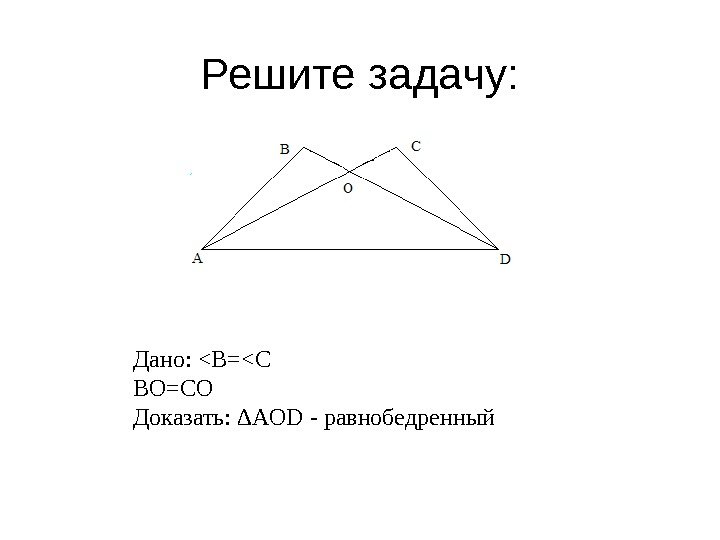
 Решите задачу: Дано: <B=<C BO=CO Доказать: ∆ AOD — равнобедренный
Решите задачу: Дано: <B=<C BO=CO Доказать: ∆ AOD — равнобедренный
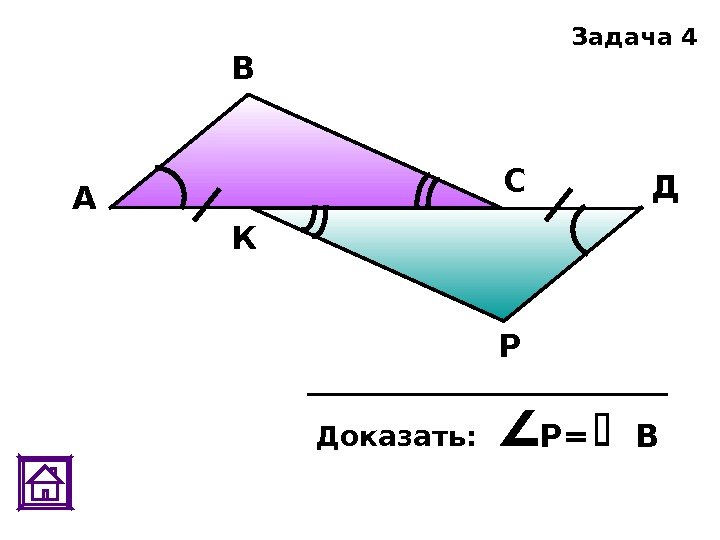
 РА В С Д К Доказать: Р= ВЗадача
РА В С Д К Доказать: Р= ВЗадача
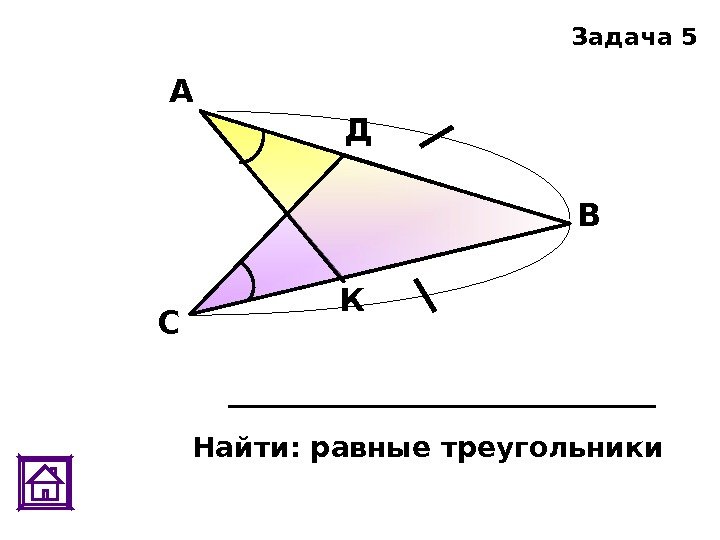
 К Д С ВА Найти: равные треугольники Задача
К Д С ВА Найти: равные треугольники Задача
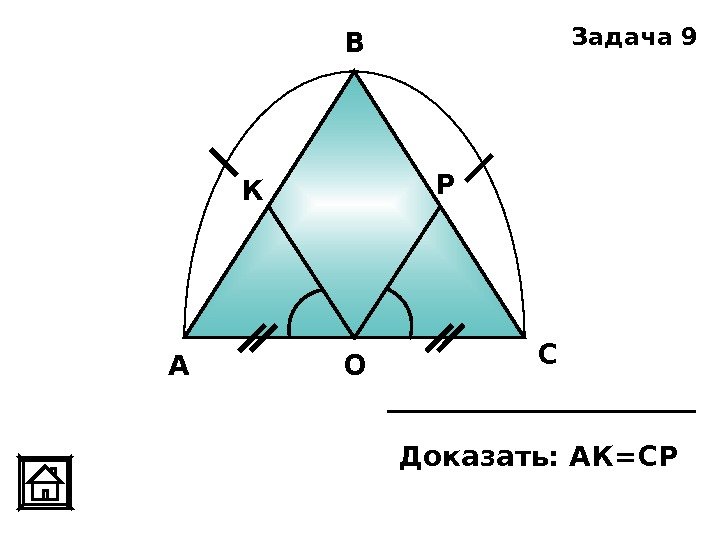
 А В С ОК Р Доказать: АК=СР Задача
А В С ОК Р Доказать: АК=СР Задача
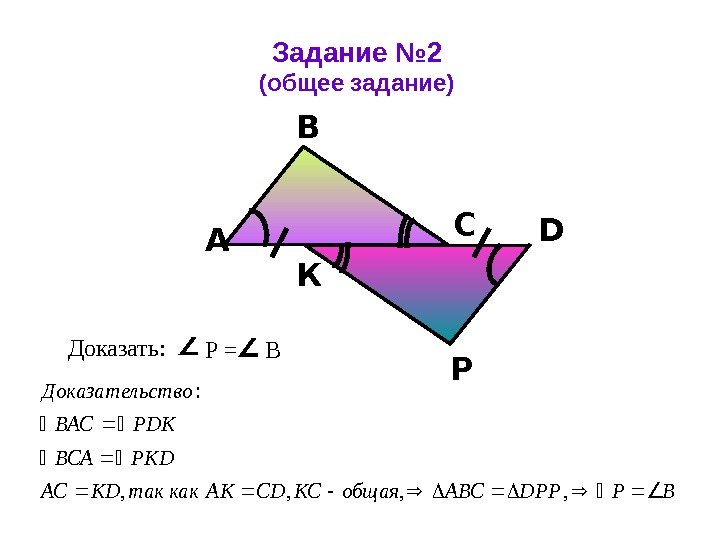
 А РВ С D К Доказать: Р = В Задание № 2 (общее задание) ВРDРРАВСобщая. КССDАКкактак. КDАС РКDВСА РDКВАС ство. Доказатель , , :
А РВ С D К Доказать: Р = В Задание № 2 (общее задание) ВРDРРАВСобщая. КССDАКкактак. КDАС РКDВСА РDКВАС ство. Доказатель , , :
