Цель урока: Изучить третий признак равенства треугольников и

Цель урока: Изучить третий признак равенства треугольников и научиться применять его при решении задач.

РА В С Д К Доказать: Р= ВЗадача

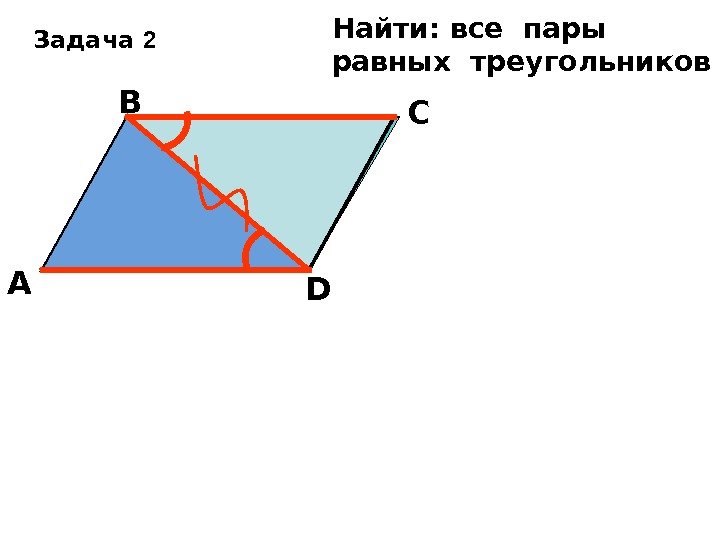А В С D Найти: все пары равных треугольников. Задача 2 О

III признак равенства треугольников по трем сторонам. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. У С Л О В И Е З А К Л Ю Ч Е Н И Е

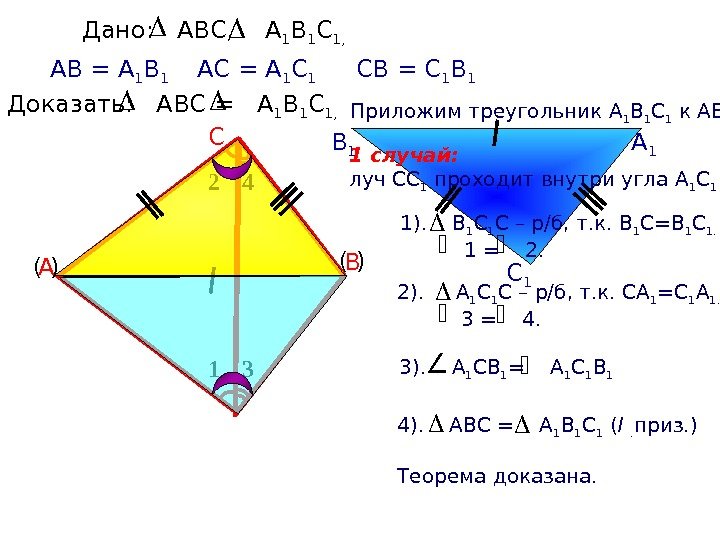А 1 В 1 С 1 Приложим треугольник А 1 В 1 С 1 к АВС. Дано: АВС, А 1 В 1 С 1, А ВСАВ = А 1 В 1 Доказать: АВС = А 1 В 1 С 1, АС = А 1 СВ = С 1 В 1 ( ) 1 32 4 4). АВС = А 1 В 1 С 1 ( I . приз. ) Теорема доказана. 3). А 1 СВ 1 = А 1 С 1 В 1 1). В 1 С – р/б, т. к. В 1 С=В 1 С 1. 1 = 2. 2). А 1 С – р/б, т. к. СА 1 =С 1 А 1. 3 = 4. 1 случай: луч СС 1 проходит внутри угла А 1 С 1 В 1.

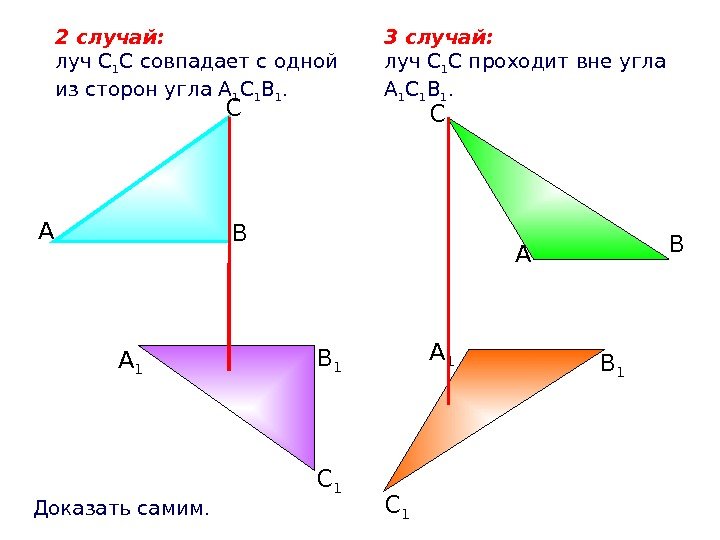2 случай: луч С 1 С совпадает с одной из сторон угла А 1 С 1 В 1. 3 случай: луч С 1 С проходит вне угла А 1 С 1 В 1. С ВА С 1 А 1 ВС А А 1 В 1 С 1 Доказать самим.

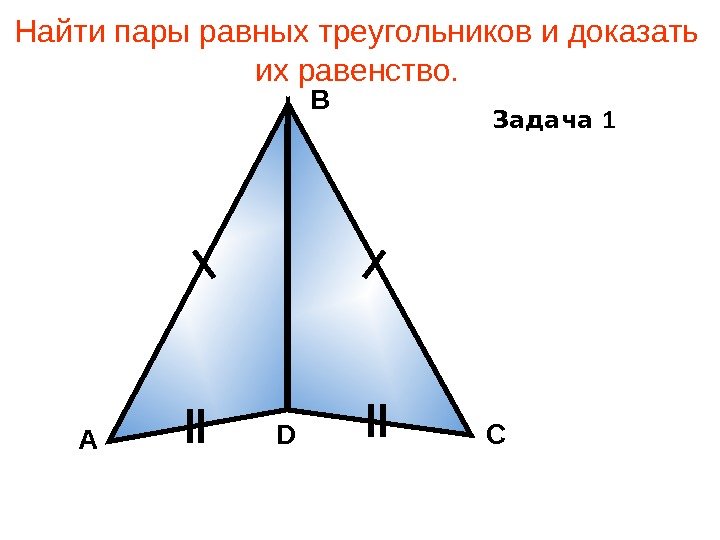Найти пары равных треугольников и доказать их равенство. А В СD Задача

Задача 2 А DВ С

Задача 3 А DВ С

А В С D Задача 4 К Р

№ 138 Дано: AB = CD; BD = AC Доказать: 1) CAD = ADB 2) BAC = С DB Доказательство: 1) Рассмотрим ∆АВ D и ∆ DC А АВ = С D (по условию) В D = АС (по условию) AD – общая 2) Рассмотрим ∆ВАС и ∆А D В АВ = CD (по условию) BD = AC (по условию) BC – общая А DСВ ∆ ABD = ∆ DCA по трём сторонам СА D = ADB ∆ ВАС = ∆А D В по трём сторонам ВАС = С