Аналитические и численные методы решения практических задач

Аналитические и численные методы решения практических задач Математическая модель задачи задана в виде уравнения f (x 1, x 2, x 3, . . . , xn) = 0 (1) или y = f (x 1, x 2, x 3, . . . , xn) (1 ) Решить задачу (1) – значит по численным значениям одних переменных найти численные значения других переменных.

При этом возможны два случая: 1. Результат решения задачи можно получить в аналитической форме. l решение квадратных уравнений ax 2 + bx + c = 0 l решение кубического уравнения вида x 3 + px + q = 0– формулы Кардана: где u и v – решения системы l вычисление определенного интеграла по формуле–Ньютона-Лейбница:

2. Результат решения задачи нельзя получить в аналитической форме. 1) вычисление корней алгебраических уравнений выше 4 -ой степени; 2) решение трансцендентных уравнений: 2 x – cos 3 x = 0; 3) «неберущиеся» интегралы: 4) нахождение значений функции, заданной таблично.

Численный метод решения задачи – определенная последовательность операций над числами, результатом которой является число или таблица чисел.

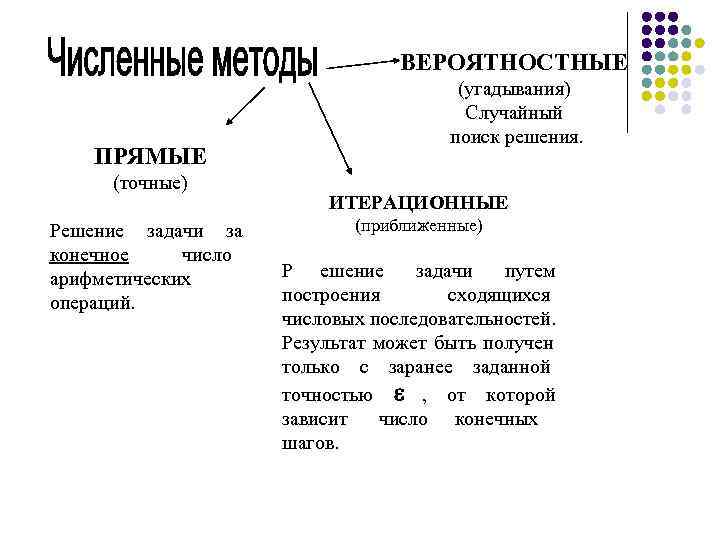
ВЕРОЯТНОСТНЫЕ (угадывания) Случайный поиск решения. ПРЯМЫЕ (точные) ИТЕРАЦИОННЫЕ Решение задачи за (приближенные) конечное число арифметических Р ешение задачи путем операций. построения сходящихся числовых последовательностей. Результат может быть получен только с заранее заданной точностью , от которой зависит число конечных шагов.

l Главная задача численных методов – выбор способа аппроксимации (приближения) и оценка точности приближенного результата решения задачи. l Алгоритм решения задачи тем или иным численным методом называется вычислительным алгоритмом.

Свойства вычислительных алгоритмов: l вычислительные алгоритмы для сложных задач можно представить как последовательность простых вычислительных алгоритмов. ; l сведение математической задачи (1) к конечномерной путем дискретизации, т. е. переходом от непрерывной математической модели y = f (x 1, x 2, x 3, . . . , xn) к дискретной модели и ее решение. Численные методы позволяют получить только приближенное решение задачи, поэтому численное решение всегда содержит погрешность.

Структура полной погрешности результата решения задачи Опр. 1. Абсолютной погрешностью числа называется модуль разности точного и приближенного значения этого числа: = |x – x*|, где x – точное значение числа, x* – приближенное значение. Опр. 2. Предельной абсолютной погрешностью называется величина x*, не меньшая абсолютной погрешности: x* . Принята следующая форма записи: х = x* x*.

Замечания: 1) предельная абсолютная погрешность всегда величина положительная; 2) предельная абсолютная погрешность указывает отрезок [x* – x*, x* + x*], внутри которого находится точное значение х: x* x x* – x* x x* + x* 3) предельная абсолютная погрешность имеет те же единицы измерения, что и приближенное число.

Задача 1 Определить предельную абсолютную погрешность числа x* = 2, 71, взятого в качестве приближенного значения точного числа х = е (е = 2, 718281…).

Задача 2 Известно, что точная площадь квадратной комнаты равна 4, 5 м 2. Когда измерили одну из ее сторон, получили 2, 1 м. С какой абсолютной погрешностью были произведены измерения?

Опр. 3. Предельной относительной погрешностью приближенного числа x* называется величина где x* ≠ 0. Предельная относительная погрешность величина безразмерная, как правило, ее представляют в процентах.

Задача 3 Найти предельные относительные погрешности в задачах 1 и 2. Полученные значения выразить в процентах.

Задача 4 Точное число х находится в промежутке [23, 07; 23, 10]. Определить его приближенное значение, абсолютную и относительную погрешности.

Общая погрешность решения задачи складывается из 3 -х видов погрешностей: l неустранимая погрешность l погрешность метода l погрешность округления Пример столбиком: 0, 476 0, 411 1, 47 26, 2 83, 111, 557 112.

ЭВМ слева направо: + 0, 476 + 0, 887 + 2, 36 + 28, 6 0, 411 1, 47 26, 2 83, 0, 887 2, 357 2, 36 28, 56 28, 6 111, 6 112. ЭВМ справа налево: + 83 + 109 + 110 26, 2 1, 47 0, 411 0, 476 109, 2 109 110, 47 110, 411 110, 476 110 В машинной арифметике законы коммутативности и дистрибутивности не всегда соблюдаются. Поэтому учесть погрешность округления при большом количестве арифметических действий практически невозможно.

Связь точного и приближенного решения задачи Пусть R – точное значение результата решения задачи R 1 – решение, соответствующее матем. модели. R R 1 R 2 - решение, получаемое при реализации численного метода в предположении отсутствия округления. R 1 R 2 R 3 - приближение к результату решения задачи, получаемое при реальных вычислениях, т. е. с округлением результатов. R 2 R 3

Тогда неустранимая погрешность, погрешность метода и вычислительная погрешности будут равны: 1= R - R 1 2= R 1 - R 2 3= R 2 - R 3 При этом: R R 1 R 2 R 3. Следовательно, R R 3, и полная погрешность результата решения задачи = R- R 3. Причем, полная погрешность получается как сумма всех погрешностей: = R - R 3 = (R - R 1) + (R 1 - R 2) + (R 2 - R 3) = 1 + 2 + 3. То есть: = 1 + 2 + 3. На практике часто приходится иметь дело с верхней оценкой полной погрешности: | | 1 + 2 + 3.

Рекомендации для снижения ошибок округления: l При + и - чисел действия необходимо начинать с наименьших по абсолютной величине значений. l Следует избегать вычитания двух близких чисел, преобразуя выражения. l Количество арифметических действий для решения задачи нужно сводить к минимуму. l Расчеты следует проводить с повышенной разрядностью.

При выборе численного метода: l Погрешность метода должна быть на порядок меньше неустранимой погрешности. Увеличение погрешности метода снижает точность, уменьшение – увеличивает время решения задачи. l Погрешность округления должна быть значительно меньше (на два порядка) погрешности метода и неустранимой погрешности.

Для оценки погрешности решения на практике: l Решить задачу различными численными методами и результаты сравнить. l Незначительно изменить исходные данные и повторно решить задачу. Результаты сравнить. Если они различаются сильно, задача или метод ее решения являются неустойчивым – выбрать другой метод.