А В СУченик показал треугольник так ЛО





tretiy_priznak_ravenstva_teugolynikov.ppt
- Размер: 2.3 Мб
- Автор: Аня Михайлова
- Количество слайдов: 24
Описание презентации А В СУченик показал треугольник так ЛО по слайдам

 А В СУченик показал треугольник так
А В СУченик показал треугольник так
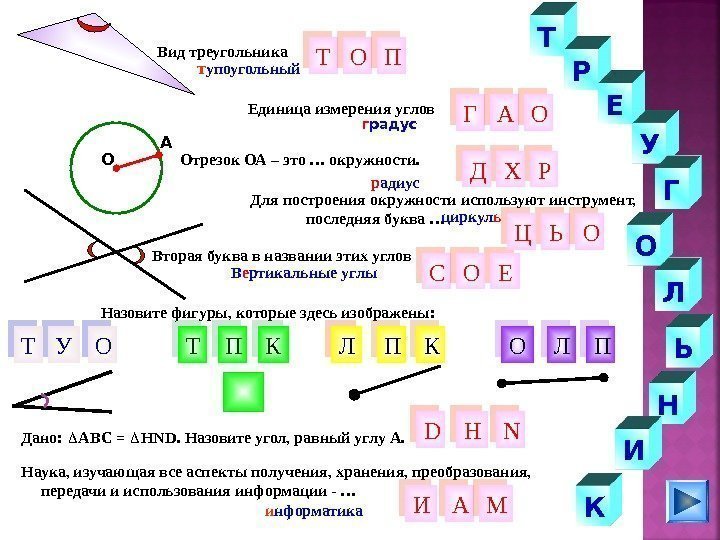
 ЛО У Нг радус Вторая буква в названии этих углов Т Р Е Г Ь И КТ Г РВид треугольника т упоугольный Отрезок ОА – это … окружности. р адиус. Единица измерения углов В е ртикальные углы Е Дано: АВС = Н ND. Назовите угол, равный углу А. Назовите фигуры, которые здесь изображены: Наука, изучающая все аспекты получения, хранения, преобразования, передачи и использования информации — … Для построения окружности используют инструмент, последняя буква … Н Ьциркул ь К ОЛУ И и нформатика О П А Л N АС ЦХ ПТ П МО Т К ПД ОО О DО А
ЛО У Нг радус Вторая буква в названии этих углов Т Р Е Г Ь И КТ Г РВид треугольника т упоугольный Отрезок ОА – это … окружности. р адиус. Единица измерения углов В е ртикальные углы Е Дано: АВС = Н ND. Назовите угол, равный углу А. Назовите фигуры, которые здесь изображены: Наука, изучающая все аспекты получения, хранения, преобразования, передачи и использования информации — … Для построения окружности используют инструмент, последняя буква … Н Ьциркул ь К ОЛУ И и нформатика О П А Л N АС ЦХ ПТ П МО Т К ПД ОО О DО А
 III признак равенства треугольников по трем сторонам. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. У С Л О В И Е З А К Л Ю Ч Е Н И Е
III признак равенства треугольников по трем сторонам. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. У С Л О В И Е З А К Л Ю Ч Е Н И Е
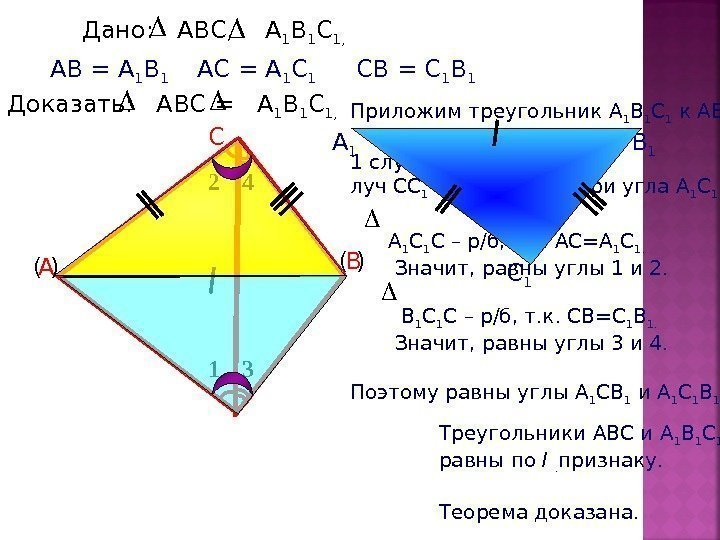
 Приложим треугольник А 1 В 1 С 1 к АВС. 1 случай: луч СС 1 проходит внутри угла А 1 С 1 В 1. А 1 С – р/б, т. к. АС=А 1 С 1. Значит, равны углы 1 и 2. В 1 С – р/б, т. к. СВ=С 1 В 1. Значит, равны углы 3 и 4. Поэтому равны углы А 1 СВ 1 и А 1 С 1 В 1 Дано: АВС, А 1 В 1 С 1, А ВСАВ = А 1 В 1 Доказать: АВС = А 1 В 1 С 1, Треугольники АВС и А 1 В 1 С 1 равны по I . признаку. Теорема доказана. АС = А 1 СВ = С 1 В 1 ( ) А 1 В 1 С
Приложим треугольник А 1 В 1 С 1 к АВС. 1 случай: луч СС 1 проходит внутри угла А 1 С 1 В 1. А 1 С – р/б, т. к. АС=А 1 С 1. Значит, равны углы 1 и 2. В 1 С – р/б, т. к. СВ=С 1 В 1. Значит, равны углы 3 и 4. Поэтому равны углы А 1 СВ 1 и А 1 С 1 В 1 Дано: АВС, А 1 В 1 С 1, А ВСАВ = А 1 В 1 Доказать: АВС = А 1 В 1 С 1, Треугольники АВС и А 1 В 1 С 1 равны по I . признаку. Теорема доказана. АС = А 1 СВ = С 1 В 1 ( ) А 1 В 1 С
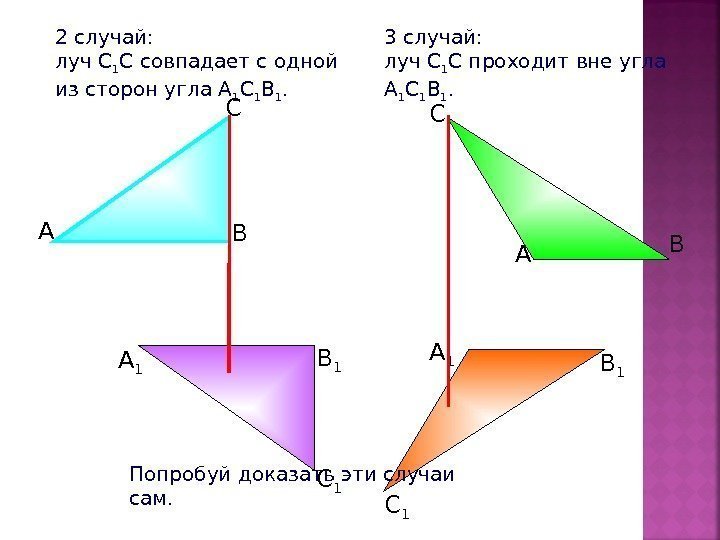
 2 случай: луч С 1 С совпадает с одной из сторон угла А 1 С 1 В 1. 3 случай: луч С 1 С проходит вне угла А 1 С 1 В 1. С ВА С 1 А 1 ВС А А 1 В 1 С 1 Попробуй доказать эти случаи сам.
2 случай: луч С 1 С совпадает с одной из сторон угла А 1 С 1 В 1. 3 случай: луч С 1 С проходит вне угла А 1 С 1 В 1. С ВА С 1 А 1 ВС А А 1 В 1 С 1 Попробуй доказать эти случаи сам.
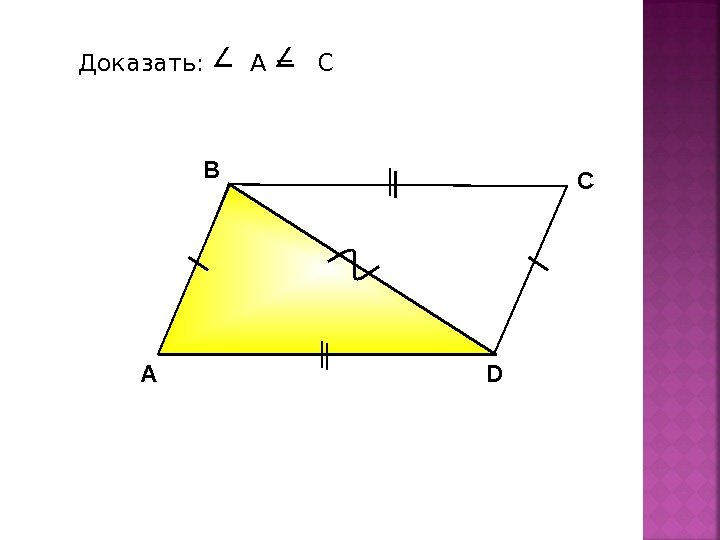
 В D С Доказать: А = С А
В D С Доказать: А = С А
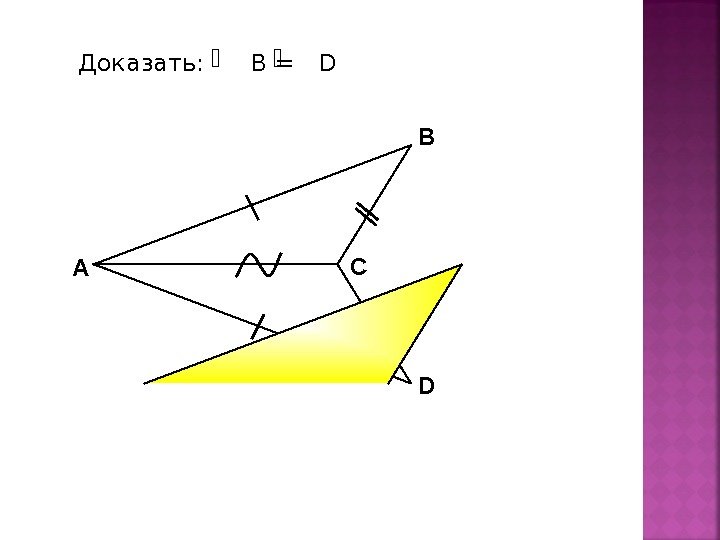
 А В DС Доказать: В =
А В DС Доказать: В =
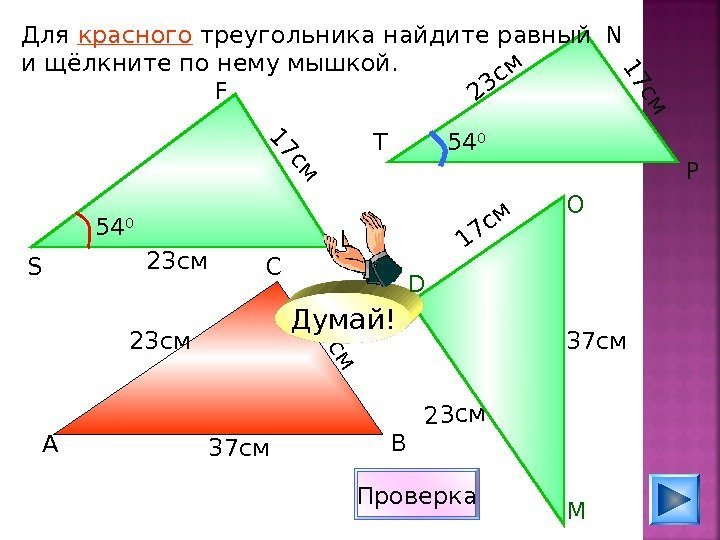
 1 7 с м 23 см. Для красного треугольника найдите равный и щёлкните по нему мышкой. 23 см 1 7 с м 17 см 1 7 см 37 см 54 0 Проверка 54 0 Думай! АS D МО С В N PT LF 37 см
1 7 с м 23 см. Для красного треугольника найдите равный и щёлкните по нему мышкой. 23 см 1 7 с м 17 см 1 7 см 37 см 54 0 Проверка 54 0 Думай! АS D МО С В N PT LF 37 см
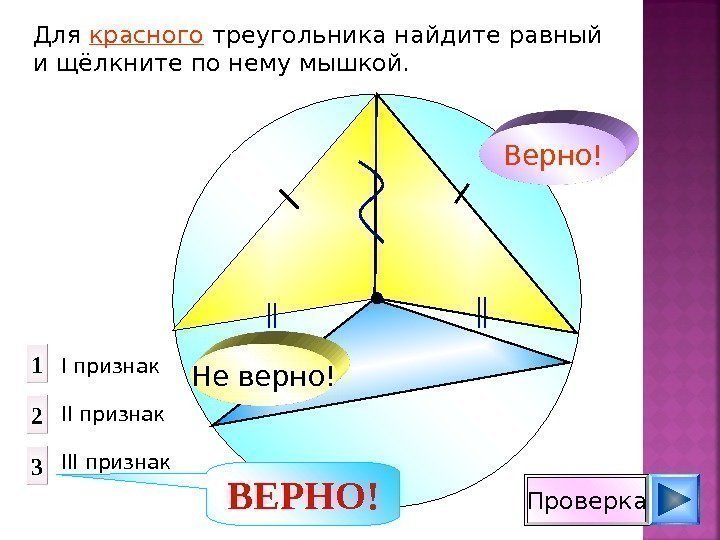
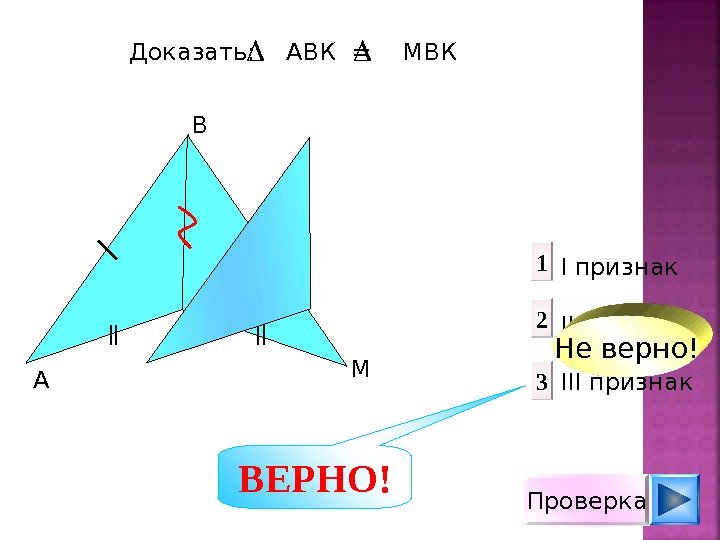
 Для красного треугольника найдите равный и щёлкните по нему мышкой. Не верно! Верно! Проверка. I признак II признак III признак 1 2 3 ВЕРНО!
Для красного треугольника найдите равный и щёлкните по нему мышкой. Не верно! Верно! Проверка. I признак II признак III признак 1 2 3 ВЕРНО!
 A MK B 1 2 3 I признак II признак III признак. Доказать: АВК = М B К Не верно! Проверка. ВЕРНО!
A MK B 1 2 3 I признак II признак III признак. Доказать: АВК = М B К Не верно! Проверка. ВЕРНО!
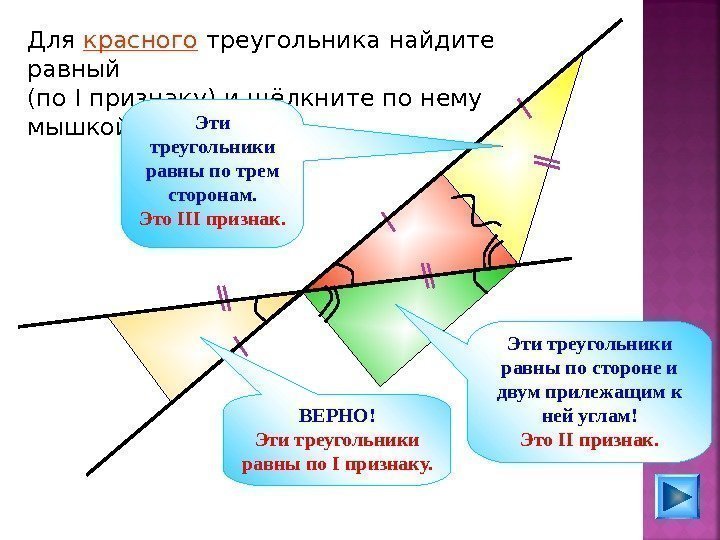
 Для красного треугольника найдите равный (по I признаку) и щёлкните по нему мышкой. Эти треугольники равны по стороне и двум прилежащим к ней углам! Это II признак. Эти треугольники равны по трем сторонам. Это III признак. ВЕРНО! Эти треугольники равны по I признаку.
Для красного треугольника найдите равный (по I признаку) и щёлкните по нему мышкой. Эти треугольники равны по стороне и двум прилежащим к ней углам! Это II признак. Эти треугольники равны по трем сторонам. Это III признак. ВЕРНО! Эти треугольники равны по I признаку.
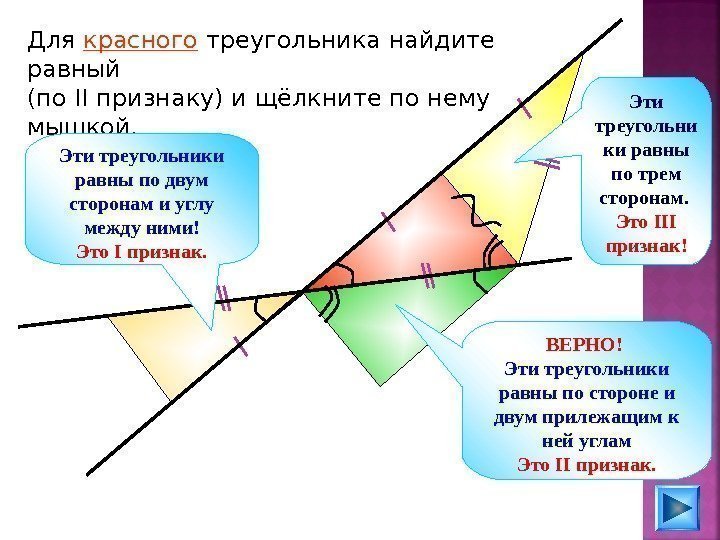
 Для красного треугольника найдите равный (по II признаку) и щёлкните по нему мышкой. ВЕРНО! Эти треугольники равны по стороне и двум прилежащим к ней углам Это II признак. Эти треугольни ки равны по трем сторонам. Это III признак!Эти треугольники равны по двум сторонам и углу между ними! Это I признак.
Для красного треугольника найдите равный (по II признаку) и щёлкните по нему мышкой. ВЕРНО! Эти треугольники равны по стороне и двум прилежащим к ней углам Это II признак. Эти треугольни ки равны по трем сторонам. Это III признак!Эти треугольники равны по двум сторонам и углу между ними! Это I признак.
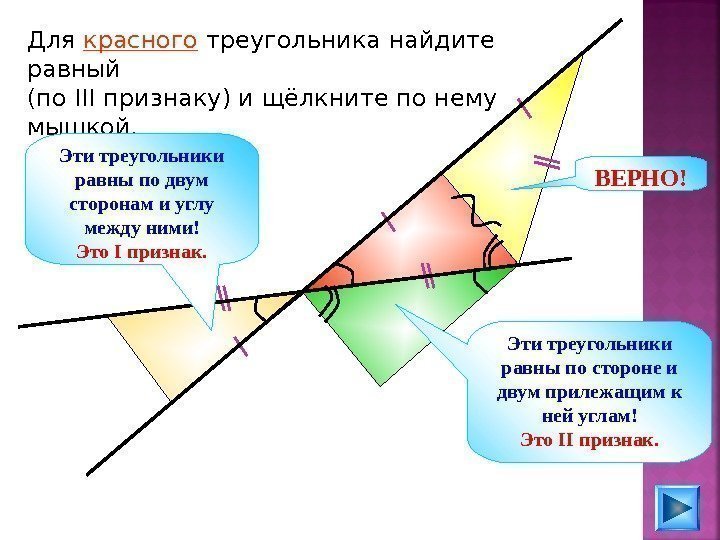
 Для красного треугольника найдите равный (по III признаку) и щёлкните по нему мышкой. Эти треугольники равны по стороне и двум прилежащим к ней углам! Это II признак. ВЕРНО!Эти треугольники равны по двум сторонам и углу между ними! Это I признак.
Для красного треугольника найдите равный (по III признаку) и щёлкните по нему мышкой. Эти треугольники равны по стороне и двум прилежащим к ней углам! Это II признак. ВЕРНО!Эти треугольники равны по двум сторонам и углу между ними! Это I признак.
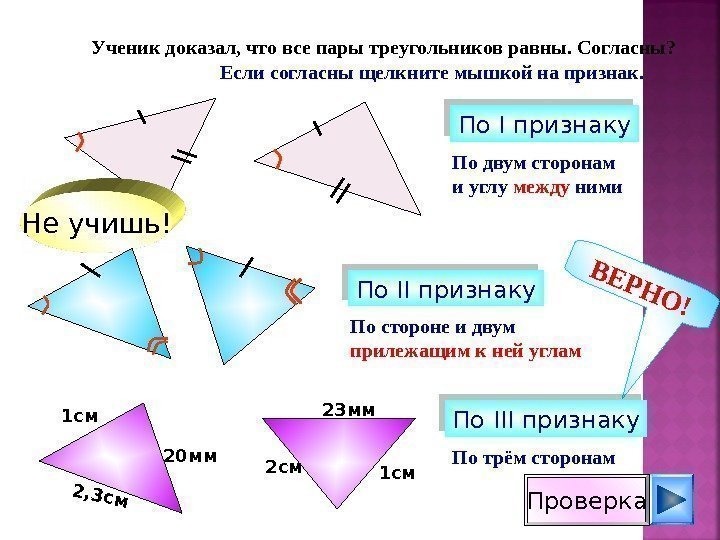
 По двум сторонам и углу между ними. По I признаку Ученик доказал, что все пары треугольников равны. Согласны? Если согласны щелкните мышкой на признак. Не учишь! 1 см 23 мм. ВЕРНО! 2, 3 см 1 см 20 мм По II признаку По III признаку. По стороне и двум прилежащим к ней углам По трём сторонам Проверка
По двум сторонам и углу между ними. По I признаку Ученик доказал, что все пары треугольников равны. Согласны? Если согласны щелкните мышкой на признак. Не учишь! 1 см 23 мм. ВЕРНО! 2, 3 см 1 см 20 мм По II признаку По III признаку. По стороне и двум прилежащим к ней углам По трём сторонам Проверка
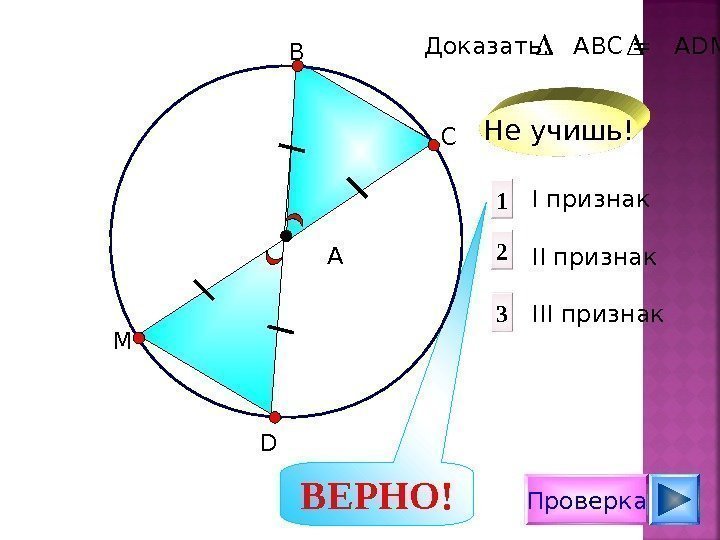
 Проверка I признак II признак III признак 21 3 Доказать: АВС = А D М DМ АВ С Не учишь! ВЕРНО!
Проверка I признак II признак III признак 21 3 Доказать: АВС = А D М DМ АВ С Не учишь! ВЕРНО!
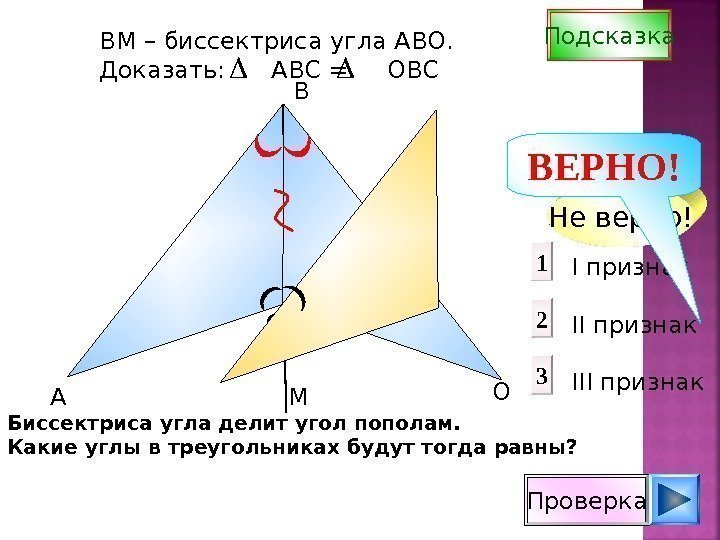
 С Проверка I признак II признак III признак 1 2 3 Не верно!B А ОВ M – биссектриса угла АВО. Доказать: АВС = ОВС Подсказка Биссектриса угла делит угол пополам. Какие углы в треугольниках будут тогда равны? ВЕРНО! М
С Проверка I признак II признак III признак 1 2 3 Не верно!B А ОВ M – биссектриса угла АВО. Доказать: АВС = ОВС Подсказка Биссектриса угла делит угол пополам. Какие углы в треугольниках будут тогда равны? ВЕРНО! М
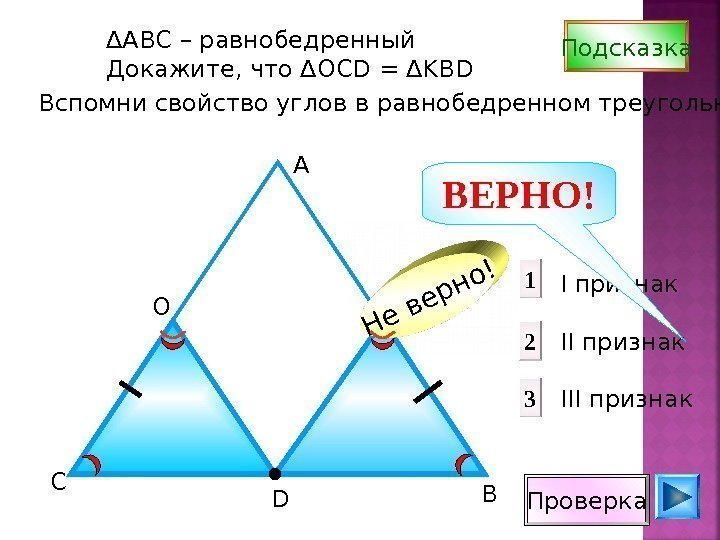
 Проверка. D ВС А О К I признак II признак III признак 1 2 3 Не верно! Подсказка Вспомни свойство углов в равнобедренном треугольнике ∆ АВС – равнобедренный Докажите, что ∆ OCD = ∆ KBD ВЕРНО!
Проверка. D ВС А О К I признак II признак III признак 1 2 3 Не верно! Подсказка Вспомни свойство углов в равнобедренном треугольнике ∆ АВС – равнобедренный Докажите, что ∆ OCD = ∆ KBD ВЕРНО!
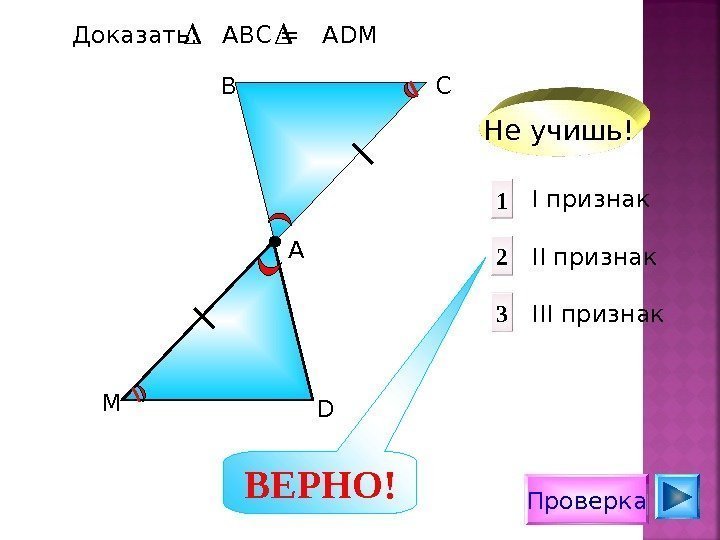
 Проверка I признак II признак III признак 1 2 3 Доказать: АВС = А D М DМ АВ С Не учишь! ВЕРНО!
Проверка I признак II признак III признак 1 2 3 Доказать: АВС = А D М DМ АВ С Не учишь! ВЕРНО!
 Каналы Экскурс «Замечательные треугольники» «По страницам всемирной сети ИНТЕРНЕТ» Из коллекции невозможных объектов.
Каналы Экскурс «Замечательные треугольники» «По страницам всемирной сети ИНТЕРНЕТ» Из коллекции невозможных объектов.
 Удивительный узел. Из коллекции невозможных объектов.
Удивительный узел. Из коллекции невозможных объектов.
 Закрученный треугольник. Из коллекции невозможных объектов.
Закрученный треугольник. Из коллекции невозможных объектов.
 Странные Комнаты Из коллекции невозможных объектов.
Странные Комнаты Из коллекции невозможных объектов.
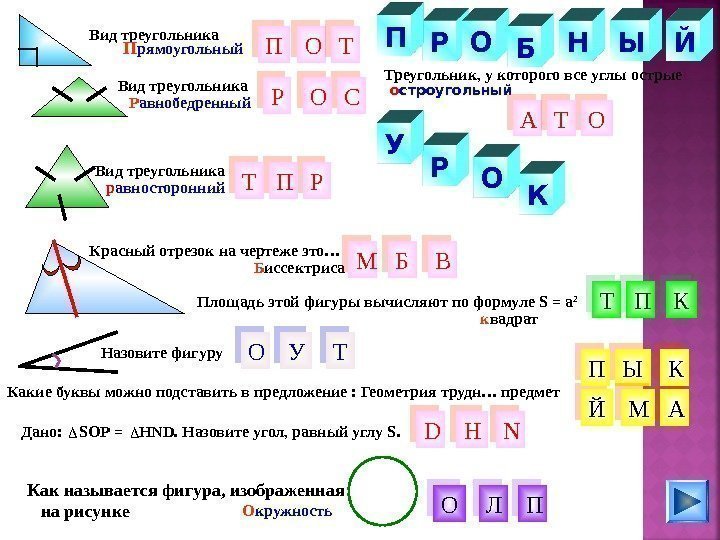
 КОР ЫН о строугольный Какие буквы можно подставить в предложение : Геометрия трудн… предмет П Р О Б Й П О РВид треугольника П рямоугольный Вид треугольника р авносторонний Треугольник, у которого все углы острые Р авнобедренный Р Дано: SOP = Н ND. Назовите угол, равный углу S. Назовите фигуру. Красный отрезок на чертеже это… НБ Б иссектриса К О ЫУ ЙО Т А Л N АС МП П Т П МО Т К ПТ В ТО DВид треугольника Площадь этой фигуры вычисляют по формуле S = a 2 Как называется фигура, изображенная на рисунке к вадрат О кружность У
КОР ЫН о строугольный Какие буквы можно подставить в предложение : Геометрия трудн… предмет П Р О Б Й П О РВид треугольника П рямоугольный Вид треугольника р авносторонний Треугольник, у которого все углы острые Р авнобедренный Р Дано: SOP = Н ND. Назовите угол, равный углу S. Назовите фигуру. Красный отрезок на чертеже это… НБ Б иссектриса К О ЫУ ЙО Т А Л N АС МП П Т П МО Т К ПТ В ТО DВид треугольника Площадь этой фигуры вычисляют по формуле S = a 2 Как называется фигура, изображенная на рисунке к вадрат О кружность У
