3. ЗАКОНОМЕРНОСТИ ПЕРЕНОСА НОСИТЕЛЕЙ ЗАРЯДА В НИЗКОРАЗМЕРНЫХ СТРУКТУРАХ





















3_carrier_transport_short.ppt
- Размер: 11.8 Mегабайта
- Количество слайдов: 48
Описание презентации 3. ЗАКОНОМЕРНОСТИ ПЕРЕНОСА НОСИТЕЛЕЙ ЗАРЯДА В НИЗКОРАЗМЕРНЫХ СТРУКТУРАХ по слайдам
 3. ЗАКОНОМЕРНОСТИ ПЕРЕНОСА НОСИТЕЛЕЙ ЗАРЯДА В НИЗКОРАЗМЕРНЫХ СТРУКТУРАХ И ПРИБОРЫ НА ИХ ОСНОВЕ 3. 1. Транспорт носителей заряда вдоль потенциальных барьеров 3. 1. 1. Интерференция электронных волн 3. 1. 2. Вольт-амперные характеристики низкоразмерных структур 3. 1. 3. Квантовый эффект Холла 3. 1. 4. Электронные приборы на интерференционном и баллистическом эффектах 3. 2. Транспорт носителей заряда через потенциальные барьеры 3. 2. 1. Одноэлектронное туннелирование и электронные приборы на этом эффекте 3. 2. 2. Резонансное туннелирование и электронные приборы на этом эффекте 3. 3. Спинтроника 3. 3. 1. Гигантское магнитосопротивление 3. 3. 2. Спин контролируемое туннелирование‑ 3. 3. 3. Управление спинами электронов в полупроводниках 3. 3. 4. Эффект Кондо 3. 3. 5. Электронные приборы на спиновых эффектах
3. ЗАКОНОМЕРНОСТИ ПЕРЕНОСА НОСИТЕЛЕЙ ЗАРЯДА В НИЗКОРАЗМЕРНЫХ СТРУКТУРАХ И ПРИБОРЫ НА ИХ ОСНОВЕ 3. 1. Транспорт носителей заряда вдоль потенциальных барьеров 3. 1. 1. Интерференция электронных волн 3. 1. 2. Вольт-амперные характеристики низкоразмерных структур 3. 1. 3. Квантовый эффект Холла 3. 1. 4. Электронные приборы на интерференционном и баллистическом эффектах 3. 2. Транспорт носителей заряда через потенциальные барьеры 3. 2. 1. Одноэлектронное туннелирование и электронные приборы на этом эффекте 3. 2. 2. Резонансное туннелирование и электронные приборы на этом эффекте 3. 3. Спинтроника 3. 3. 1. Гигантское магнитосопротивление 3. 3. 2. Спин контролируемое туннелирование‑ 3. 3. 3. Управление спинами электронов в полупроводниках 3. 3. 4. Эффект Кондо 3. 3. 5. Электронные приборы на спиновых эффектах
 3. 1. 1. 1. Интерференция электронных волн 33. 1. Транспорт носителей заряда вдоль потенциальных барьеров 1 =A 1 exp(i 1 ) 2 =A 2 exp(i 2 ) W = 1 + 2 2 =A 1 2 +A 2 2 + 2 A 1 *A 2 cos( 1 — 2 ) Фазовая интерференция ( phase interference of electron waves ) Эффект Ааронова-Бома ( Aharonov‑Bohm effect ) 0 =h/e– the quantum of the magnetic flux Y. Aharonov, D. Bohm, Significance of electromagnetic potentials in the quantum theory, Phys. Rev. 115 (3), 485 -491 (1959). = 2 ( / 0 ) http: //www. physics. gatech. edu/davidovic/nano 0_files/image 002. jpg
3. 1. 1. 1. Интерференция электронных волн 33. 1. Транспорт носителей заряда вдоль потенциальных барьеров 1 =A 1 exp(i 1 ) 2 =A 2 exp(i 2 ) W = 1 + 2 2 =A 1 2 +A 2 2 + 2 A 1 *A 2 cos( 1 — 2 ) Фазовая интерференция ( phase interference of electron waves ) Эффект Ааронова-Бома ( Aharonov‑Bohm effect ) 0 =h/e– the quantum of the magnetic flux Y. Aharonov, D. Bohm, Significance of electromagnetic potentials in the quantum theory, Phys. Rev. 115 (3), 485 -491 (1959). = 2 ( / 0 ) http: //www. physics. gatech. edu/davidovic/nano 0_files/image 002. jpg
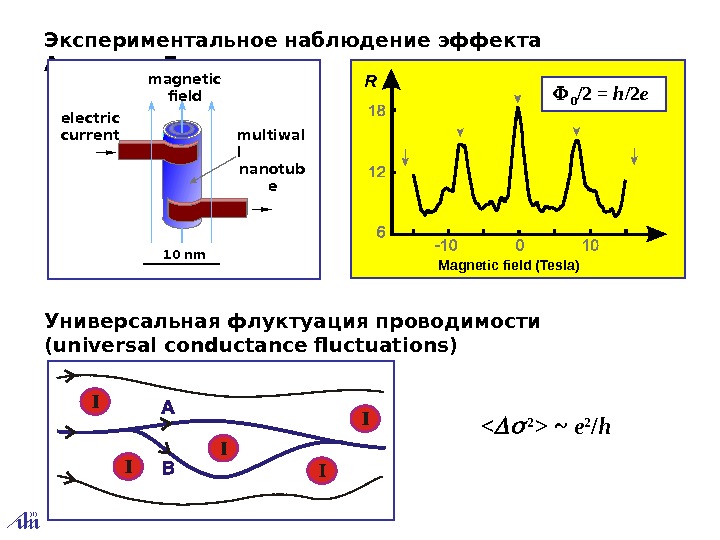
 Экспериментальное наблюдение эффекта Ааронова-Бома R Magnetic field (Tesla)magnetic field multiwal l nanotub eelectric current 10 nm 0 /2 = h /2 e Универсальная флуктуация проводимости ( universal conductance fluctuations ) ~e 2 / h
Экспериментальное наблюдение эффекта Ааронова-Бома R Magnetic field (Tesla)magnetic field multiwal l nanotub eelectric current 10 nm 0 /2 = h /2 e Универсальная флуктуация проводимости ( universal conductance fluctuations ) ~e 2 / h
 3. 1. 2. 2. Вольт-амперные характеристики низкоразмерных структур Формализм Ландауэра-Бютикера ( Landauer‑B ü ttiker formalism ) I i = 2 ev i ( dn i / d. E) i i = i — 0 dn i / d. E= 1/ hv i I i = (2 e / h ) i ii N mn mnijij. N mn mnii. TTRR , , , ji iiji. NTR ij jijiiii. TRN h e I])[( 2 ij jijiii. TR h e I])1[( 2 R. Landauer, Spatial variation of currents and fields due to localized scatters in metallic conduction, IBMJ. Res. Dev. 1 (6), 223 -231 (1957); M. Büttiker, Four-terminal phase-coherent conductance, Phys. Rev. Lett. 57 (14), 1761 -1764 (1986). i =e. V i
3. 1. 2. 2. Вольт-амперные характеристики низкоразмерных структур Формализм Ландауэра-Бютикера ( Landauer‑B ü ttiker formalism ) I i = 2 ev i ( dn i / d. E) i i = i — 0 dn i / d. E= 1/ hv i I i = (2 e / h ) i ii N mn mnijij. N mn mnii. TTRR , , , ji iiji. NTR ij jijiiii. TRN h e I])[( 2 ij jijiii. TR h e I])1[( 2 R. Landauer, Spatial variation of currents and fields due to localized scatters in metallic conduction, IBMJ. Res. Dev. 1 (6), 223 -231 (1957); M. Büttiker, Four-terminal phase-coherent conductance, Phys. Rev. Lett. 57 (14), 1761 -1764 (1986). i =e. V i
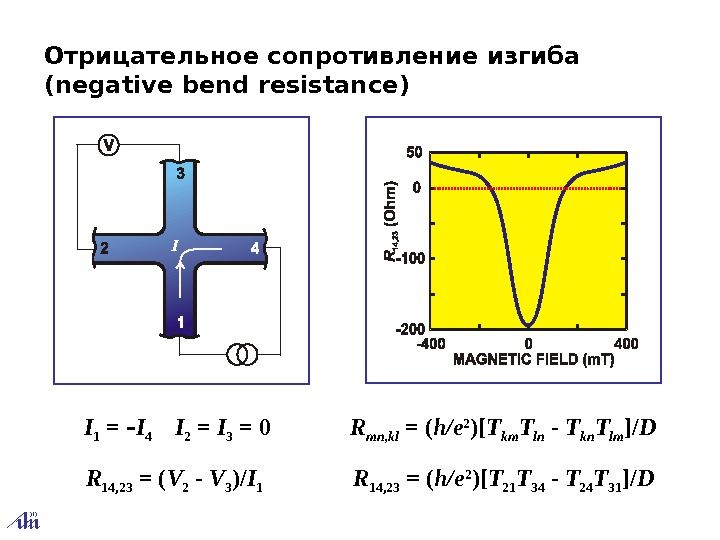
 Отрицательное сопротивление изгиба ( negative bend resistance ) I 1 = ‑ I 4 I 2 = I 3 = 0 R 14, 23 = ( V 2 — V 3 )/ I 1 R mn, kl = ( h/e 2 )[ T km T ln -T kn T lm ]/ D R 14, 23 = ( h/e 2 )[ T 21 T 34 -T 24 T 31 ]/
Отрицательное сопротивление изгиба ( negative bend resistance ) I 1 = ‑ I 4 I 2 = I 3 = 0 R 14, 23 = ( V 2 — V 3 )/ I 1 R mn, kl = ( h/e 2 )[ T km T ln -T kn T lm ]/ D R 14, 23 = ( h/e 2 )[ T 21 T 34 -T 24 T 31 ]/
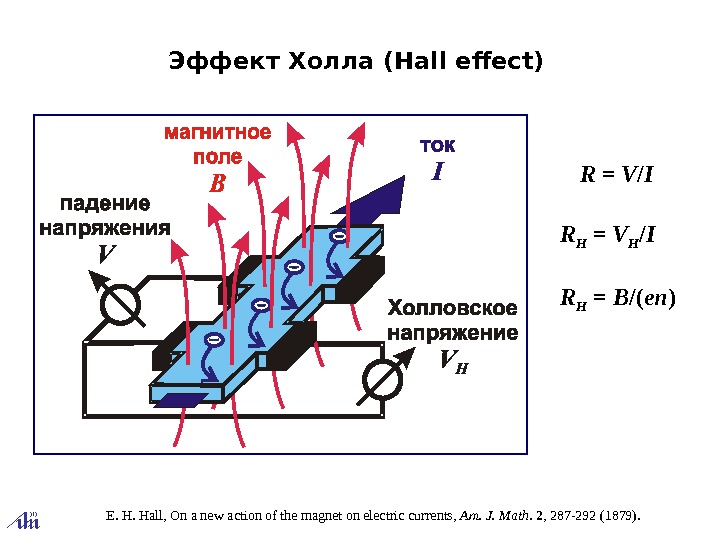
 Эффект Холла ( Hall effect ) R = V / I R H = V H / I R H = B /( en ) E. H. Hall, On a new action of the magnet on electric currents, Am. J. Math. 2 , 287 -292 (1879).
Эффект Холла ( Hall effect ) R = V / I R H = V H / I R H = B /( en ) E. H. Hall, On a new action of the magnet on electric currents, Am. J. Math. 2 , 287 -292 (1879).
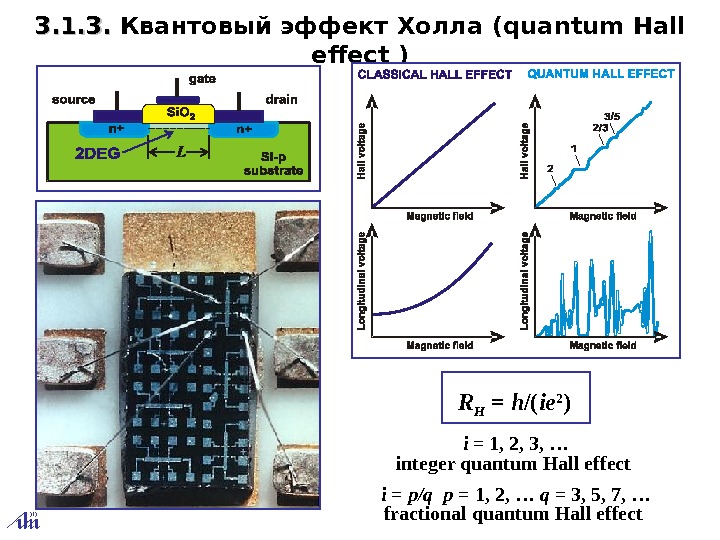
 3. 1. 3. . Квантовый эффект Холла (quantum Hall effect ) i = 1, 2, 3, … integer quantum Hall effect R H = h /( ie 2 ) i = p/q p = 1, 2, … q = 3, 5, 7, … fractional quantum Hall effect
3. 1. 3. . Квантовый эффект Холла (quantum Hall effect ) i = 1, 2, 3, … integer quantum Hall effect R H = h /( ie 2 ) i = p/q p = 1, 2, … q = 3, 5, 7, … fractional quantum Hall effect
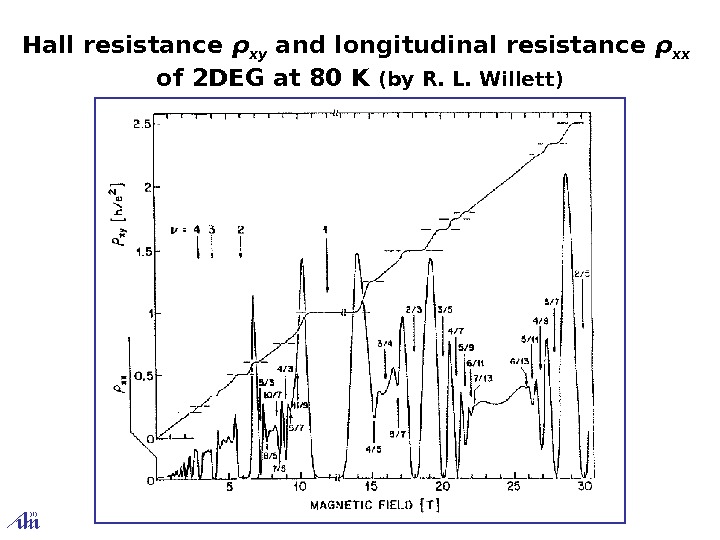
 Hall resistance ρ xy and longitudinal resistance ρ xx of 2 DEG at 80 K (by R. L. Willett )
Hall resistance ρ xy and longitudinal resistance ρ xx of 2 DEG at 80 K (by R. L. Willett )
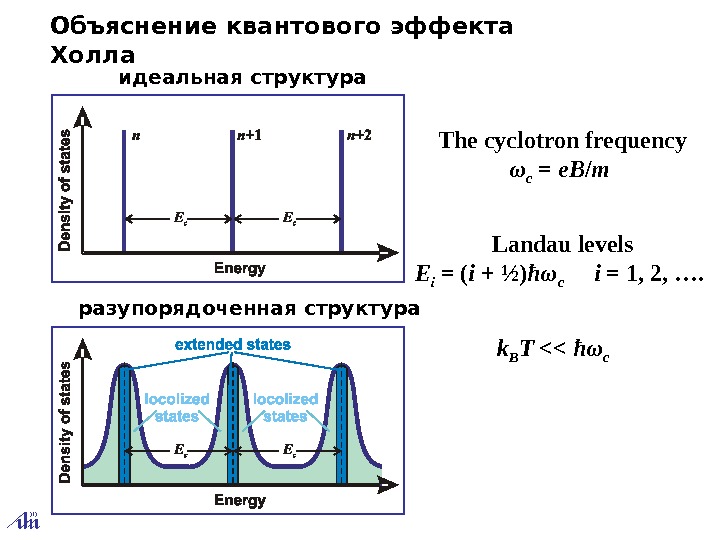
 Объяснение квантового эффекта Холла The cyclotron frequency ω c = e. B / m Landau levels E i = ( i + ½) ħω c i = 1, 2, …. k B T << ħω c идеальная структура разупорядоченная структура
Объяснение квантового эффекта Холла The cyclotron frequency ω c = e. B / m Landau levels E i = ( i + ½) ħω c i = 1, 2, …. k B T << ħω c идеальная структура разупорядоченная структура
 for the discovery of the quantized Hall effect Klausvon. Klitzing (1943) Max-Planck-Institut für Festkörperforschung Stuttgart, Germany The Nobel Prize in P hysics , 198 5 K. von Klitzing, G. Dorda, M. Pepper, New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance, Phys. Rev. Lett. 45 (6), 494 -497 (1980) – the integer quantum Hall effect. From the History of the Quantum Hall Effect
for the discovery of the quantized Hall effect Klausvon. Klitzing (1943) Max-Planck-Institut für Festkörperforschung Stuttgart, Germany The Nobel Prize in P hysics , 198 5 K. von Klitzing, G. Dorda, M. Pepper, New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance, Phys. Rev. Lett. 45 (6), 494 -497 (1980) – the integer quantum Hall effect. From the History of the Quantum Hall Effect
 for their discovery of a new form of quantum fluid with fractionally charged excitations. The Nobel Prize in P hysics , 19 9 8 From the History of the Quantum Hall Effect D. C. Tsui, H. L. Störmer, A. C. Gossard, Two-dimensional magnetotransport in the extreme quantum limit, Phys. Rev. Lett. 48 (22), 1559 -1562 (1982) and R. B. Laughlin, Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations, Phys. Rev. Lett. 50 (18), 1395 -1398 (1983) – the fractional quantum Hall effect. Robert. B. Laughli n (1950) Stanford University Stanford, CA, USA Horst. L. Störmer (1943) Columbia University New York, NY, USA Daniel. C. Tsui (1939) Princeton University Princeton, NJ, US
for their discovery of a new form of quantum fluid with fractionally charged excitations. The Nobel Prize in P hysics , 19 9 8 From the History of the Quantum Hall Effect D. C. Tsui, H. L. Störmer, A. C. Gossard, Two-dimensional magnetotransport in the extreme quantum limit, Phys. Rev. Lett. 48 (22), 1559 -1562 (1982) and R. B. Laughlin, Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations, Phys. Rev. Lett. 50 (18), 1395 -1398 (1983) – the fractional quantum Hall effect. Robert. B. Laughli n (1950) Stanford University Stanford, CA, USA Horst. L. Störmer (1943) Columbia University New York, NY, USA Daniel. C. Tsui (1939) Princeton University Princeton, NJ, US
 co n d u ctan ce , e 2/h. L 0 12 3. 1. 4. . Электронные приборы на интерференционн ом и баллистическом эффектах Квантовый интерференционный транзистор ( q ua ntum i n terference transistor ) single mode multi mode co n d u ctan ce , e 2/h L
co n d u ctan ce , e 2/h. L 0 12 3. 1. 4. . Электронные приборы на интерференционн ом и баллистическом эффектах Квантовый интерференционный транзистор ( q ua ntum i n terference transistor ) single mode multi mode co n d u ctan ce , e 2/h L
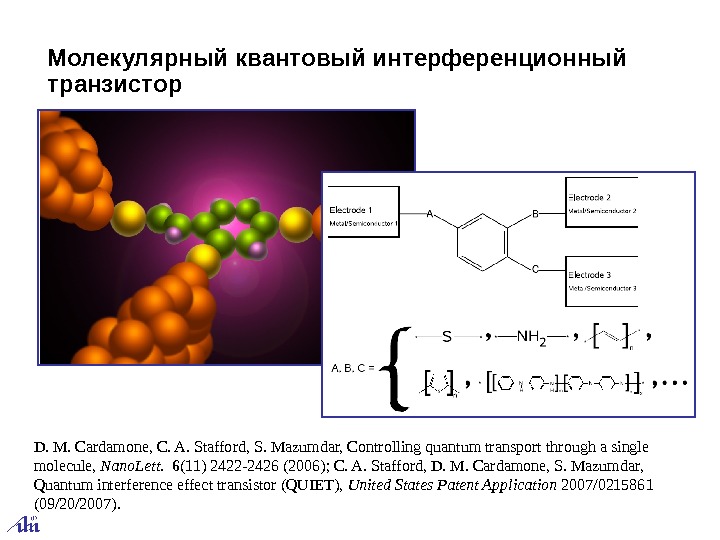
 Молекулярный к вантовый интерференционный транзистор D. M. Cardamone, C. A. Stafford, S. Mazumdar, Controlling quantum transport through a single molecule, Nano. Lett. 6 (11) 2422 -2426 (2006); C. A. Stafford, D. M. Cardamone, S. Mazumdar, Quantum interference effect transistor (QUIET), United. States. Patent. Application 2007/0215861 (09/20/2007).
Молекулярный к вантовый интерференционный транзистор D. M. Cardamone, C. A. Stafford, S. Mazumdar, Controlling quantum transport through a single molecule, Nano. Lett. 6 (11) 2422 -2426 (2006); C. A. Stafford, D. M. Cardamone, S. Mazumdar, Quantum interference effect transistor (QUIET), United. States. Patent. Application 2007/0215861 (09/20/2007).
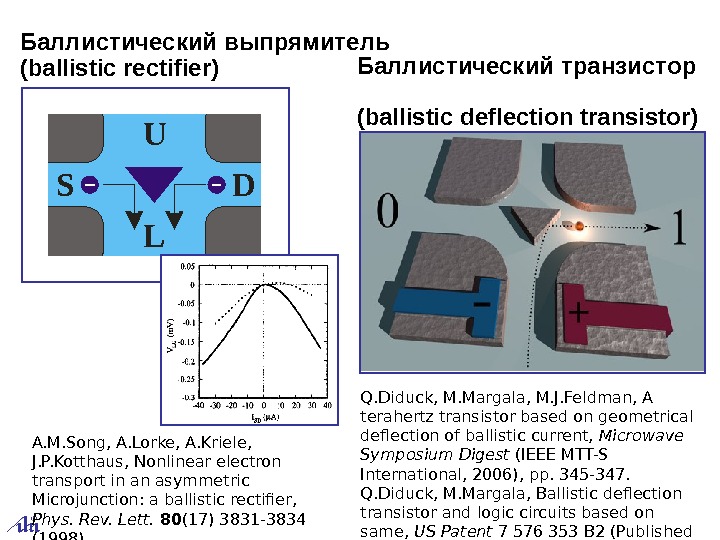
 Баллистический транзистор ( ballistic deflection transistor) Q. Diduck, M. Margala, M. J. Feldman, A terahertz transistor based on geometrical deflection of ballistic current, Microwave Symposium Digest (IEEE MTT-S International, 2006), pp. 345 -347. Q. Diduck, M. Margala, Ballistic deflection transistor and logic circuits based on same, US Patent 7 576 353 B 2 (Published August 18, 2009). Баллистический выпрямитель ( ballistic rectifier) A. M. Song, A. Lorke, A. Kriele, J. P. Kotthaus, Nonlinear electron transport in an asymmetric Microjunction: a ballistic rectifier, Phys. Rev. Lett. 80 (17) 3831 -3834 (1998). U L S
Баллистический транзистор ( ballistic deflection transistor) Q. Diduck, M. Margala, M. J. Feldman, A terahertz transistor based on geometrical deflection of ballistic current, Microwave Symposium Digest (IEEE MTT-S International, 2006), pp. 345 -347. Q. Diduck, M. Margala, Ballistic deflection transistor and logic circuits based on same, US Patent 7 576 353 B 2 (Published August 18, 2009). Баллистический выпрямитель ( ballistic rectifier) A. M. Song, A. Lorke, A. Kriele, J. P. Kotthaus, Nonlinear electron transport in an asymmetric Microjunction: a ballistic rectifier, Phys. Rev. Lett. 80 (17) 3831 -3834 (1998). U L S
 Q = e /2 3. 3. 22. . 1. 1. Одноэлектронное туннелирование и электронные приборы на этом эффекте 33. . 22. . Транспорт носителей заряда через потенциальны е барьер ы single electron tunneling Firsttheory: K. K. Likharev, A. B. Zorin, Theory of Bloch wave oscillations in small ‑ Josephson junctions, J. Low. Temp. Phys. 59 (3/4), 347 -382 (1985) D. V. Averin, K. K. Likharev, Coulomb blockade of tunneling and coherent oscillations in small tunnel junctions, J. Low. Temp. Phys. 62 (2), 345 -372 (1986) Firstexperiment: T. A. Fulton, G. J. Dolan, Observation of single-electron charging effects in small tunneling junctions, Phys. Rev. Lett. 59 (1), 109 -112 (1987)
Q = e /2 3. 3. 22. . 1. 1. Одноэлектронное туннелирование и электронные приборы на этом эффекте 33. . 22. . Транспорт носителей заряда через потенциальны е барьер ы single electron tunneling Firsttheory: K. K. Likharev, A. B. Zorin, Theory of Bloch wave oscillations in small ‑ Josephson junctions, J. Low. Temp. Phys. 59 (3/4), 347 -382 (1985) D. V. Averin, K. K. Likharev, Coulomb blockade of tunneling and coherent oscillations in small tunnel junctions, J. Low. Temp. Phys. 62 (2), 345 -372 (1986) Firstexperiment: T. A. Fulton, G. J. Dolan, Observation of single-electron charging effects in small tunneling junctions, Phys. Rev. Lett. 59 (1), 109 -112 (1987)
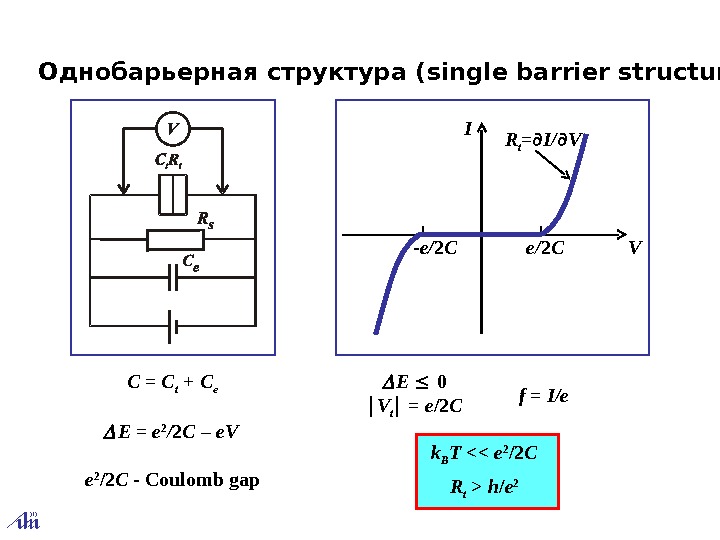
 E=e 2 / 2 C–e. V C = C t + C e E 0 V t = e /2 C e 2 /2 C — Coulomb gap. Однобарьерная структура ( single barrier structure) f = I / e k B T < h / e 2 VI R t = ∂ I/ ∂ V e/ 2 C-e/
E=e 2 / 2 C–e. V C = C t + C e E 0 V t = e /2 C e 2 /2 C — Coulomb gap. Однобарьерная структура ( single barrier structure) f = I / e k B T < h / e 2 VI R t = ∂ I/ ∂ V e/ 2 C-e/
 Двухбарьерная структура ( double barrier structure) E= 1/2[( e / C+ V o ) 2 C – V o 2 C ] V C ( e /2 C+ V o )/C R Coulomb staircase VI e/ 2 C-e/ 2 C V 0 I 1 3 5 VC/e. N =0 -1< N <1 -2< N C L C=C L +C R
Двухбарьерная структура ( double barrier structure) E= 1/2[( e / C+ V o ) 2 C – V o 2 C ] V C ( e /2 C+ V o )/C R Coulomb staircase VI e/ 2 C-e/ 2 C V 0 I 1 3 5 VC/e. N =0 -1< N <1 -2< N C L C=C L +C R
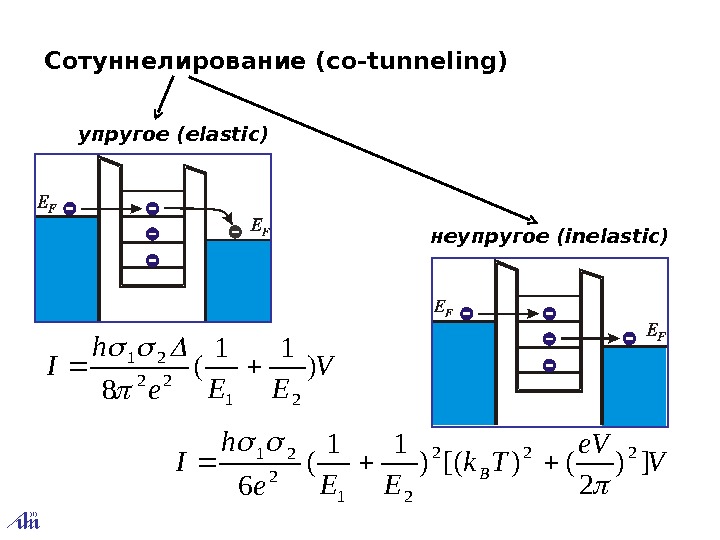
 Сотуннелирование ( co-tunneling) упругое ( elastic ) неупругое ( inelastic )V EEe h I) 11 ( 821 22 21 V e. V Tk EEe h IB]) 2 ()[() 11 (
Сотуннелирование ( co-tunneling) упругое ( elastic ) неупругое ( inelastic )V EEe h I) 11 ( 821 22 21 V e. V Tk EEe h IB]) 2 ()[() 11 (
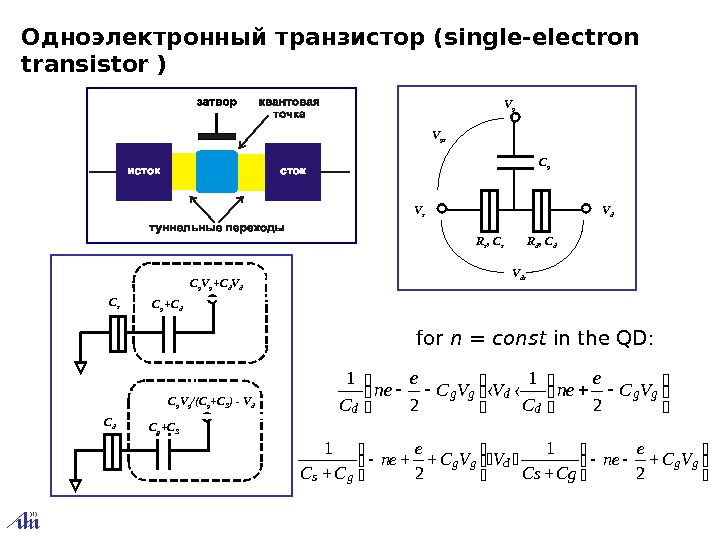
 R d , C d. R s , C s V ds. V s V d. V gs V g C g gg d dgg d VC e ne C VVC e ne C 2 1 ggdgg gs VC e ne Cg. Cs VVC e ne CC 2 1 for n = const in the QD: C g V g +C d V d C g +C d. C s C g +C SC d C g V g /(C g +C S )-V d. Одноэлектронный транзистор ( single ‑ electron transistor )
R d , C d. R s , C s V ds. V s V d. V gs V g C g gg d dgg d VC e ne C VVC e ne C 2 1 ggdgg gs VC e ne Cg. Cs VVC e ne CC 2 1 for n = const in the QD: C g V g +C d V d C g +C d. C s C g +C SC d C g V g /(C g +C S )-V d. Одноэлектронный транзистор ( single ‑ electron transistor )
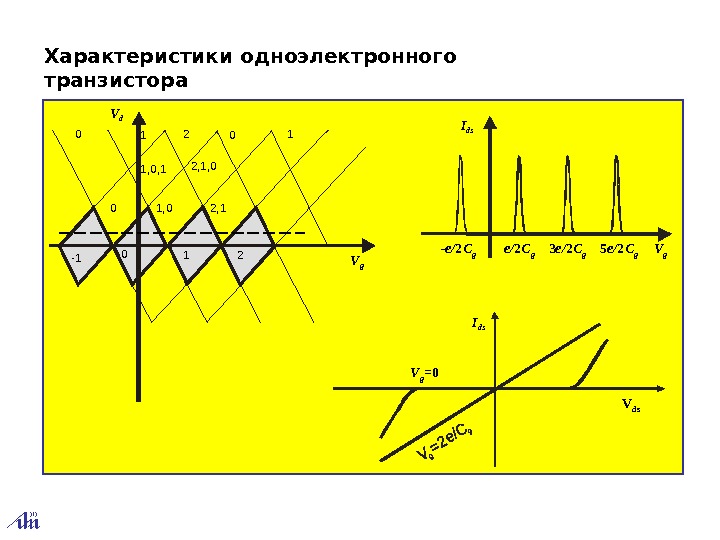
 Характеристики одноэлектронного транзистора 0 1 2 0 1 1, 0, 1 2, 1, 0 0 1, 0 2, 1 -1 0 1 2 V g. V d -e/ 2 C g 3 e/ 2 C g 5 e/ 2 C g V g. I ds V g = 0 V ds. I ds
Характеристики одноэлектронного транзистора 0 1 2 0 1 1, 0, 1 2, 1, 0 0 1, 0 2, 1 -1 0 1 2 V g. V d -e/ 2 C g 3 e/ 2 C g 5 e/ 2 C g V g. I ds V g = 0 V ds. I ds
 Одноэлектронный Ti транзистор K. Matsumoto, M. Ishii, K. Segawa, Y. Oka , B. J. Vartanian , J. S. Harris , Room temperature operation of a single electron transistor made by the scanning tunneling microscope nanooxidation process for the Ti. Ox/Ti system , Appl. Phys. Lett. 68 (1), 34 -36 ( 1996 ).
Одноэлектронный Ti транзистор K. Matsumoto, M. Ishii, K. Segawa, Y. Oka , B. J. Vartanian , J. S. Harris , Room temperature operation of a single electron transistor made by the scanning tunneling microscope nanooxidation process for the Ti. Ox/Ti system , Appl. Phys. Lett. 68 (1), 34 -36 ( 1996 ).
 www. ece. umd. edu/labs/ebl/ Одноэлектронный In. As транзистор 1948 Первый Ge транзистор
www. ece. umd. edu/labs/ebl/ Одноэлектронный In. As транзистор 1948 Первый Ge транзистор
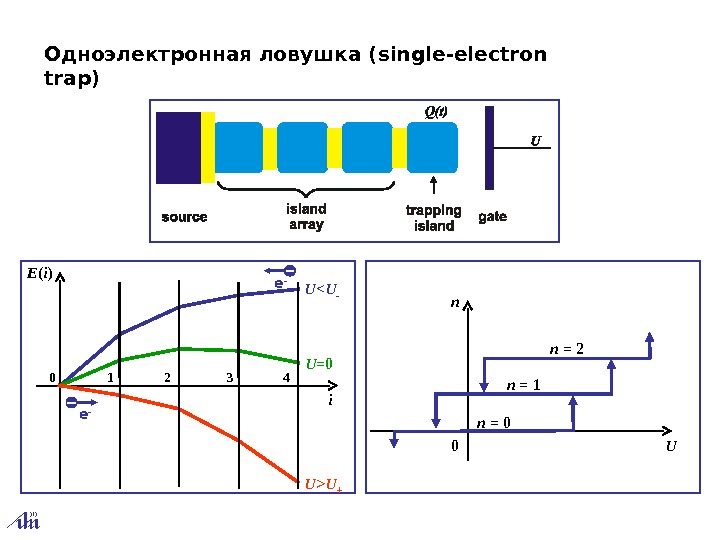
 Одноэлектронная ловушка ( single ‑ electron trap ) e — 0 1 2 3 4 U =0 U>U +U<U — i. E ( i ) n 0 Un= 2 n= 1 n=
Одноэлектронная ловушка ( single ‑ electron trap ) e — 0 1 2 3 4 U =0 U>U +U<U — i. E ( i ) n 0 Un= 2 n= 1 n=
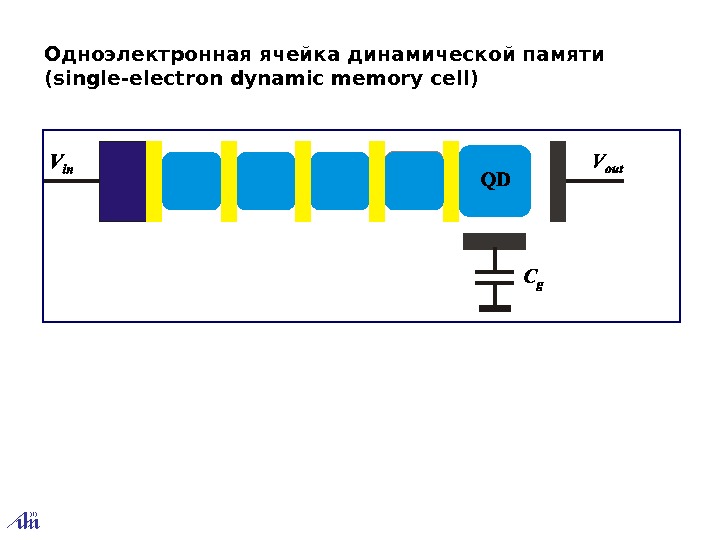
 Одноэлектронная ячейка динамической памяти ( single ‑ electron dynamic memory cell )
Одноэлектронная ячейка динамической памяти ( single ‑ electron dynamic memory cell )
 Одноэлектронный турникет ( single ‑ electron turnstile ) Одноэлектронный генератор накачки ( single ‑ electron generator )
Одноэлектронный турникет ( single ‑ electron turnstile ) Одноэлектронный генератор накачки ( single ‑ electron generator )
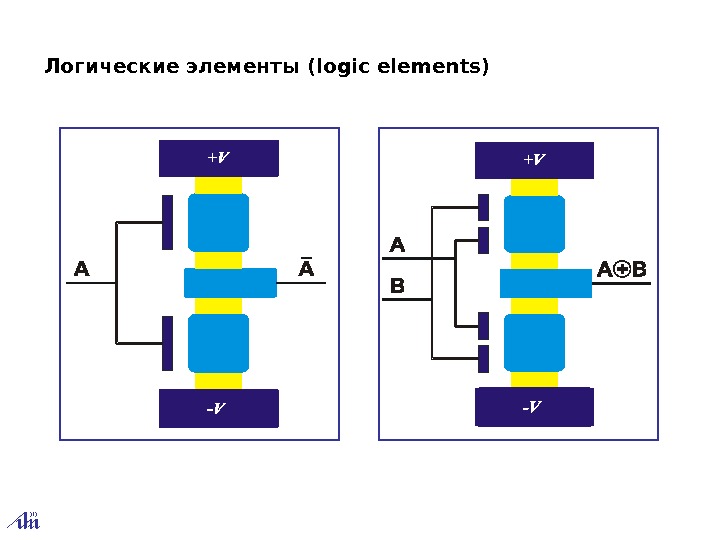
 Логические элементы (logic elements)
Логические элементы (logic elements)
()[( E F E 11 E F e V 2 E 1 /e 00 3))]('()()[(](/docs//3_carrier_transport_short_images/3_carrier_transport_short_26.jpg) E F E 11 E F e V 2 E 1 /e 00 3))](‘()()[( 4 z zzyx k E Ef. ETdkdkdk e J E ‘ = E + e. V 3. 3. 22. 2. 2. . Резонансное туннелирование и электронные приборы на этом эффекте (resonant tunneling) 2 22 1*2 am E E F e V
E F E 11 E F e V 2 E 1 /e 00 3))](‘()()[( 4 z zzyx k E Ef. ETdkdkdk e J E ‘ = E + e. V 3. 3. 22. 2. 2. . Резонансное туннелирование и электронные приборы на этом эффекте (resonant tunneling) 2 22 1*2 am E E F e V
 Резонансно-туннельный диод ( resonant tunneling diode ) C(V) I(V) R S VI C Depletion approximation V L. Esaki, R. Tsu, Superlattice and negative differential conductivity in semiconductors, IBMJ. Res. Dev. 14 (1), 61 -65 (1970) The Nobel Prize in P hysics , 19 73 for his experimental discoveries regarding tunneling phenomena in semiconductors
Резонансно-туннельный диод ( resonant tunneling diode ) C(V) I(V) R S VI C Depletion approximation V L. Esaki, R. Tsu, Superlattice and negative differential conductivity in semiconductors, IBMJ. Res. Dev. 14 (1), 61 -65 (1970) The Nobel Prize in P hysics , 19 73 for his experimental discoveries regarding tunneling phenomena in semiconductors
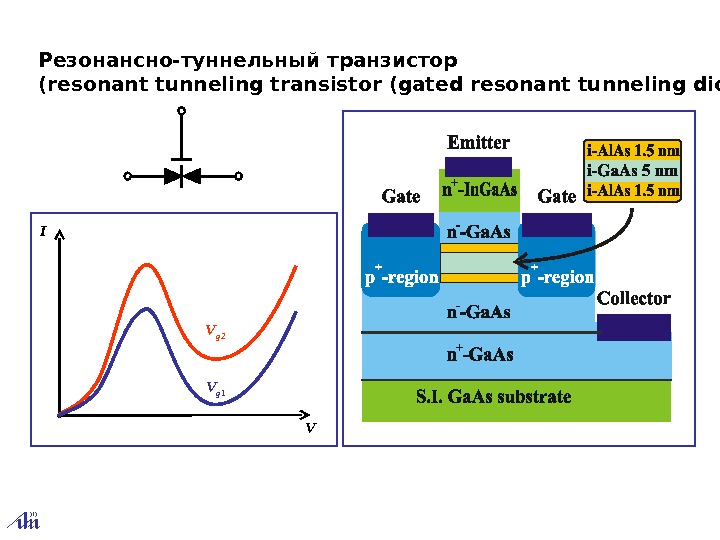
 Резонансно-туннельный транзистор (resonant tunneling transistor (gated resonant tunneling diode)) VI V g 1 V g
Резонансно-туннельный транзистор (resonant tunneling transistor (gated resonant tunneling diode)) VI V g 1 V g
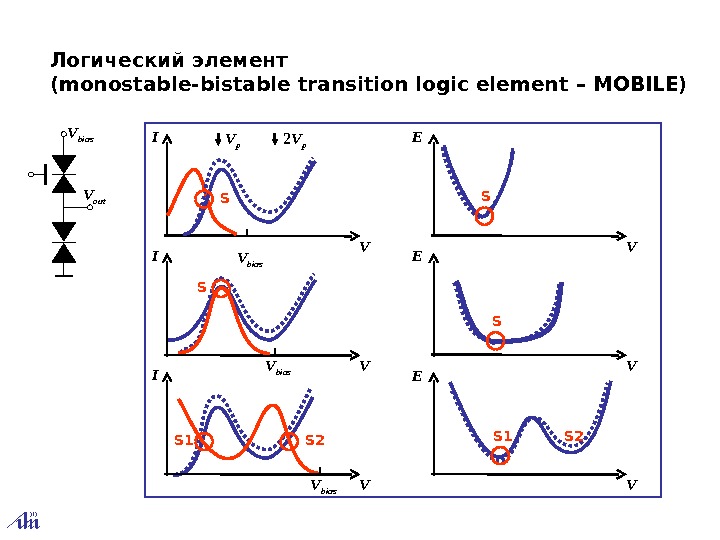
 Логический элемент (monostable ‑ bistable transition logic element – MOBILE) S V p 2 V p V bias VI VE S V bias VI S 1 S 2 VE S 1 S 2 V bias V out
Логический элемент (monostable ‑ bistable transition logic element – MOBILE) S V p 2 V p V bias VI VE S V bias VI S 1 S 2 VE S 1 S 2 V bias V out
 33. . Спинтроника (spintronics) область науки и техники, занимающаяся созданием, исследованием и применением электронных приборов, в которых спин электрона наравне с его зарядом используется для обработки информации
33. . Спинтроника (spintronics) область науки и техники, занимающаяся созданием, исследованием и применением электронных приборов, в которых спин электрона наравне с его зарядом используется для обработки информации
 3. 3. 1. 1. Гигантское магнитосопротивление (giant magnetoresistance effect) Протекание тока в плоскости структуры (current‑in‑plane – CIP ) Протекание тока перпендикулярно плоскости структуры (current ‑ perpendicul ar‑ to‑plane – CPP )
3. 3. 1. 1. Гигантское магнитосопротивление (giant magnetoresistance effect) Протекание тока в плоскости структуры (current‑in‑plane – CIP ) Протекание тока перпендикулярно плоскости структуры (current ‑ perpendicul ar‑ to‑plane – CPP )
 The Nobel Prize in P hysics , 2007 From the History of the Giant Magnetoresistance Effect Albert Fert (1938) Université Paris-Sud Orsay, France Peter Grünberg (1939) Forschungszentrum Jülich, Germany for the discovery of Giant Magnetoresistance M. N. Baibich, J. M. Broto, A. Fert, F. N. Van Dau, F. Petroff, Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices, Phys. Rev. Lett. 61 (21), 2472 -2475 (1988). G. Binasch, P. Gr ü nberg, F. Saurenbach, W. Zinn, Enhancedmagnetoresistanceinlayeredmagnetic structureswithantiferromagneticinterlayerexchange , Phys. Rev. B 39 (7), 4828 -4830 ( 1989 ).
The Nobel Prize in P hysics , 2007 From the History of the Giant Magnetoresistance Effect Albert Fert (1938) Université Paris-Sud Orsay, France Peter Grünberg (1939) Forschungszentrum Jülich, Germany for the discovery of Giant Magnetoresistance M. N. Baibich, J. M. Broto, A. Fert, F. N. Van Dau, F. Petroff, Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices, Phys. Rev. Lett. 61 (21), 2472 -2475 (1988). G. Binasch, P. Gr ü nberg, F. Saurenbach, W. Zinn, Enhancedmagnetoresistanceinlayeredmagnetic structureswithantiferromagneticinterlayerexchange , Phys. Rev. B 39 (7), 4828 -4830 ( 1989 ).
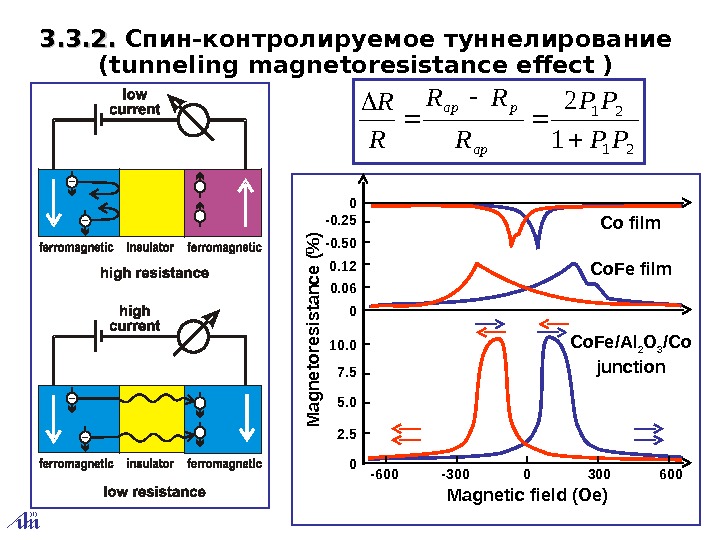
 21 21 1 2 PP PP R RR R R ap pap 3. 3. 2. . Спин‑контролируемое туннелирование (tunneling magnetoresistance effect ) Co film Co. Fe/Al 2 O 3 /Co junction Magnetic field (Oe) M ag n e to resistan ce (% )00 -0. 25 -0. 50 0. 12 0. 06 0 10. 0 7. 5 5. 0 2. 5 0 -600 —
21 21 1 2 PP PP R RR R R ap pap 3. 3. 2. . Спин‑контролируемое туннелирование (tunneling magnetoresistance effect ) Co film Co. Fe/Al 2 O 3 /Co junction Magnetic field (Oe) M ag n e to resistan ce (% )00 -0. 25 -0. 50 0. 12 0. 06 0 10. 0 7. 5 5. 0 2. 5 0 -600 —
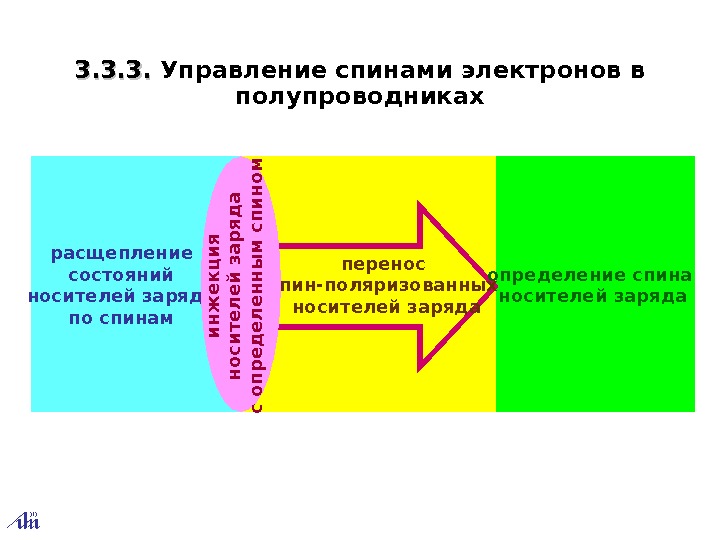
 расщепление состояний носителей заряда по спинам 3. 3. 3. . Управление спинами электронов в полупроводниках перенос спин-поляризованных носителей заряда определение спина носителей зарядаи н ж е к ц и я н о с и т е л е й з а р я д а с о п р е д е л е н н ы м с п и н о м
расщепление состояний носителей заряда по спинам 3. 3. 3. . Управление спинами электронов в полупроводниках перенос спин-поляризованных носителей заряда определение спина носителей зарядаи н ж е к ц и я н о с и т е л е й з а р я д а с о п р е д е л е н н ы м с п и н о м
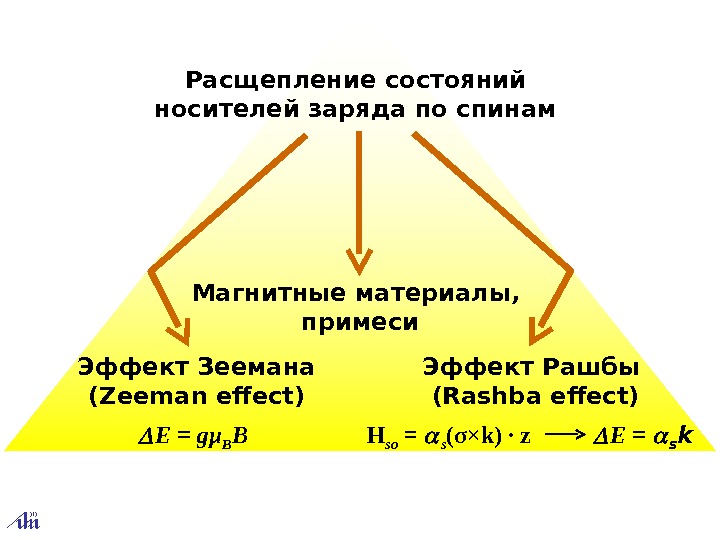
 Расщепление состояний носителей заряда по спинам Эффект Зеемана ( Zeemaneffect ) Эффект Рашбы ( Rashba effect ) E=gμ B B H so = s ( σ × k) · z E= s k Магнитные материалы, примеси
Расщепление состояний носителей заряда по спинам Эффект Зеемана ( Zeemaneffect ) Эффект Рашбы ( Rashba effect ) E=gμ B B H so = s ( σ × k) · z E= s k Магнитные материалы, примеси
 Перенос спин-поляризованных носителей заряда (механизмы спин-релаксации в полупроводниках) Механизм Бира-Аронова-Пикуса ( Bir — Aronov — Pikus mechanism ) Механизм Эллиота-Яфета ( Elliot — Yafet mechanism ) Механизм Дьяконова — Перела (D’yakonov — Perel m echanism) Следствие обменного взаимодействия и рекомбинации электронов и дырок. Низкие Т , р -полупроводники. Следствие спин-орбитального рассеивания, при столкновении электронов с фононами или примесями. Низкие и умеренные Т. Следствие спин-расщепления зоны проводимости. Повышенные Т. a a a. B k. Ba s. N p. N N p v va. N 3 502143 0 kpgk sog so ks. EE E E A E 11 22 3 2 21 T E Ap gs T Em p p g z s 22 2 1 сверхтонкое взаимодействие спинов электронов и спинов ядер ( hyperfine interaction of the electron spins and nuclear spins )
Перенос спин-поляризованных носителей заряда (механизмы спин-релаксации в полупроводниках) Механизм Бира-Аронова-Пикуса ( Bir — Aronov — Pikus mechanism ) Механизм Эллиота-Яфета ( Elliot — Yafet mechanism ) Механизм Дьяконова — Перела (D’yakonov — Perel m echanism) Следствие обменного взаимодействия и рекомбинации электронов и дырок. Низкие Т , р -полупроводники. Следствие спин-орбитального рассеивания, при столкновении электронов с фононами или примесями. Низкие и умеренные Т. Следствие спин-расщепления зоны проводимости. Повышенные Т. a a a. B k. Ba s. N p. N N p v va. N 3 502143 0 kpgk sog so ks. EE E E A E 11 22 3 2 21 T E Ap gs T Em p p g z s 22 2 1 сверхтонкое взаимодействие спинов электронов и спинов ядер ( hyperfine interaction of the electron spins and nuclear spins )
 Определение спина носителей заряда
Определение спина носителей заряда
 Temperature. R esistancesuper- conductivity T c T K Квантовая точка в режиме Кондо ρ = AT 5 – B ln T + C Kondo rise 3. 3. 4. 4. Эффект Кондо ( Kondo e ffect )
Temperature. R esistancesuper- conductivity T c T K Квантовая точка в режиме Кондо ρ = AT 5 – B ln T + C Kondo rise 3. 3. 4. 4. Эффект Кондо ( Kondo e ffect )
 3. 3. 5. . Электронные приборы на спиновых эффектах Спиновые транзисторы спиновой полевой транзистор ( spin field — effect transistor ) S. Datta, B. Das, Electronic analog of the electrooptic modulator, Appl. Phys. Lett. 56 (7), 665 -667 (1990). =2 s m * E y L / ħ 2 J=J 0 cos 2 ( /2 ) Fsd. FEe. VEf. EEfd. E h e J
3. 3. 5. . Электронные приборы на спиновых эффектах Спиновые транзисторы спиновой полевой транзистор ( spin field — effect transistor ) S. Datta, B. Das, Electronic analog of the electrooptic modulator, Appl. Phys. Lett. 56 (7), 665 -667 (1990). =2 s m * E y L / ħ 2 J=J 0 cos 2 ( /2 ) Fsd. FEe. VEf. EEfd. E h e J
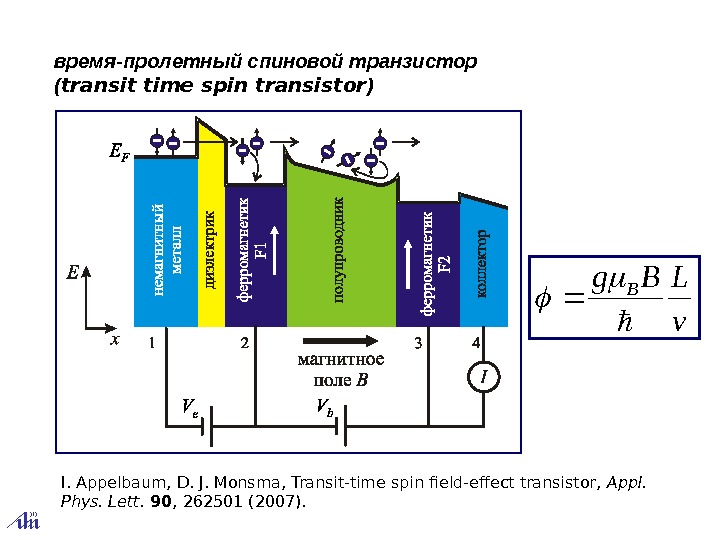
 время-пролетный спиновой транзистор ( transit time spin transistor ) I. Appelbaum, D. J. Monsma, Transit-time spin field-effect transistor, Appl. Phys. Lett. 90 , 262501 (2007). v LBg.
время-пролетный спиновой транзистор ( transit time spin transistor ) I. Appelbaum, D. J. Monsma, Transit-time spin field-effect transistor, Appl. Phys. Lett. 90 , 262501 (2007). v LBg.
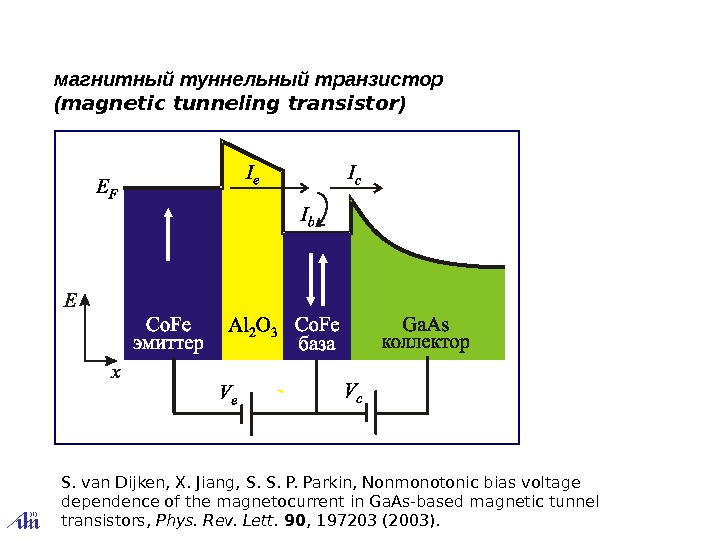
 магнитный туннельный транзистор ( magnetic tunneling transistor ) S. van Dijken, X. Jiang, S. S. P. Parkin, Nonmonotonic bias voltage dependence of the magnetocurrent in Ga. As-based magnetic tunnel transistors, Phys. Rev. Lett. 90 , 197203 (2003).
магнитный туннельный транзистор ( magnetic tunneling transistor ) S. van Dijken, X. Jiang, S. S. P. Parkin, Nonmonotonic bias voltage dependence of the magnetocurrent in Ga. As-based magnetic tunnel transistors, Phys. Rev. Lett. 90 , 197203 (2003).
 спин-вентильный транзистор ( spin-valve transistor ) -40 -20 0 4020 Magnetic field (Oe)04812 C ollector current (arb. U nits) D. J. Monsma, J. C. Lodder, T. J. A. Popma, B. Dieny, Perpendicular hot electron spin-valve effect in a new magnetic field sensor: the spin-valve transistor, Phys. Rev. Lett. 74 (26), 5260 -5263 (1995).
спин-вентильный транзистор ( spin-valve transistor ) -40 -20 0 4020 Magnetic field (Oe)04812 C ollector current (arb. U nits) D. J. Monsma, J. C. Lodder, T. J. A. Popma, B. Dieny, Perpendicular hot electron spin-valve effect in a new magnetic field sensor: the spin-valve transistor, Phys. Rev. Lett. 74 (26), 5260 -5263 (1995).
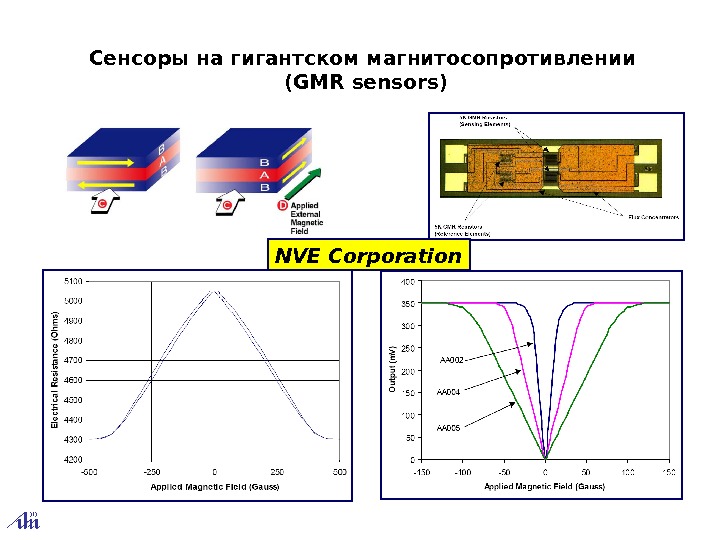
 Сенсоры на гигантском магнитосопротивлении ( GMR sensors ) NVE Corporation
Сенсоры на гигантском магнитосопротивлении ( GMR sensors ) NVE Corporation
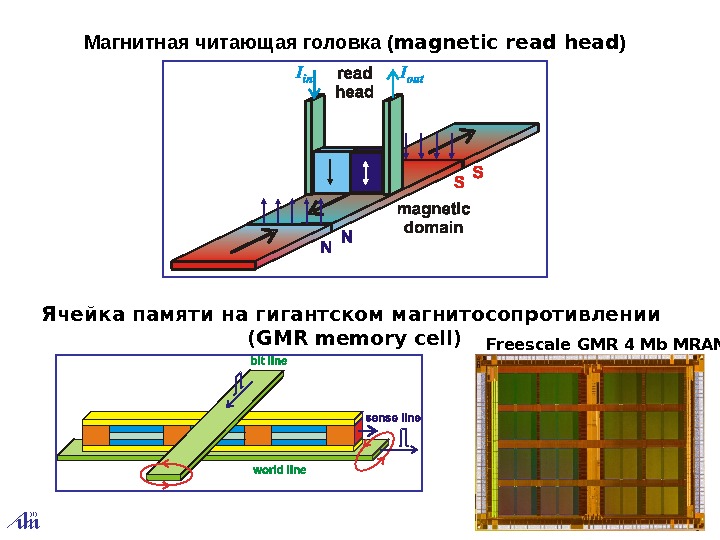
 Магнитная читающая головка ( magnetic read head ) Ячейка памяти на гигантском магнитосопротивлении ( GMR memory cell ) Freescale GMR 4 Mb MRAM
Магнитная читающая головка ( magnetic read head ) Ячейка памяти на гигантском магнитосопротивлении ( GMR memory cell ) Freescale GMR 4 Mb MRAM
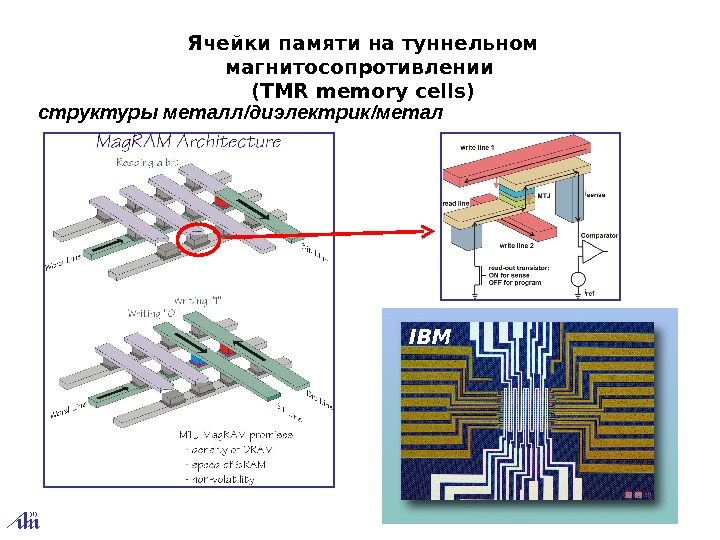
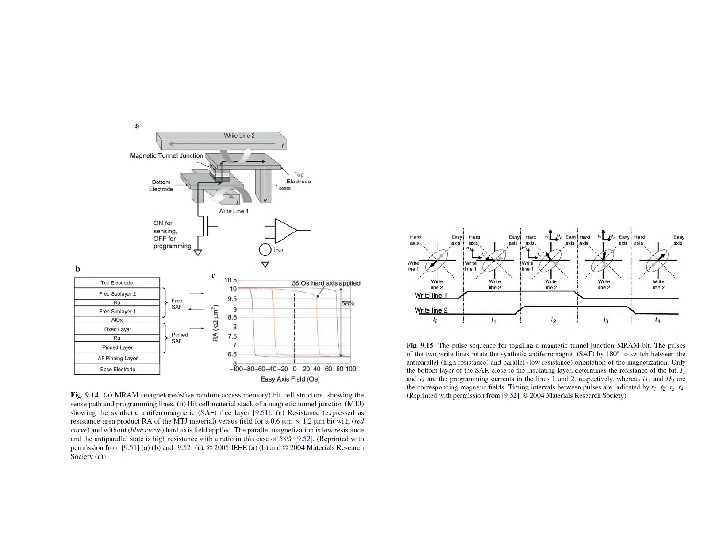
 Ячейки памяти на туннельном магнитосопротивлении ( TMR memory cells ) IBMструктуры металл / диэлектрик / метал
Ячейки памяти на туннельном магнитосопротивлении ( TMR memory cells ) IBMструктуры металл / диэлектрик / метал

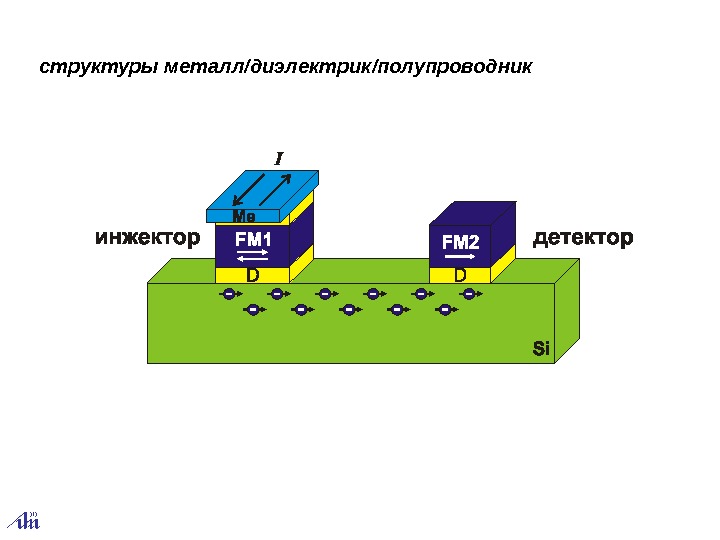
 структуры металл / диэлектрик / полупроводник
структуры металл / диэлектрик / полупроводник
