3. 2 Аномальные поля 3. 2. 1

3. 2 Аномальные поля

3. 2. 1 Точечный источник и контакт двух сред ‘ ‘1 r. Q U 21 UU x U 2 21 111 A A’ 1 2 U 1 U 2 d. Обозначим : 2 1 I Q Будем искать решение в виде : Г. У. : d QQ d. U ‘ )( 1 222 zyxr 222 )2(‘ zydxr r QQ U » 2 d QQ d. U » )( 2 »’QQНа границе :

12 12 12 k. Коэффициент отражения: 2 1 33 1 1 »1 ‘ )2(‘1 d QQ d d. Q d Qd r dx. Q r Qx jn 2 22 22 »’ d QQ jn 21 »’ QQQQ )(‘)(1212 QQ )( )( ‘ 12 12 QQ ‘1 12 1 rk r. QU Решение : r k QU

212 21 )2(1 dx k x. QE 2 12 2 1 x k QEДифференцирование по направлению х дает поле, отвечающее идеальной градиент-установке )2(1 12 1 dx k x. QU x k QU 12 2 1 На поверхности земли :

Проведем преобразования применительно к случаю профилирования : A 1 2 d x’ x 12 12 12; ‘; kd. AOdxx. AOx 0 1. x’ 0 A 1 2 AOx 2. A 1 2 d x’ 12 12 12; ‘; kd. AOx 0 3. 1. 2 12 212 12 211 ‘2 1 1 )’2( 1 )2( 1 AO x k AO Q x. AO k AO Q xd k x QE 212 1 2 12 12 11 AO k Q x k QE 2. 2 12 222 12 223 ‘2 1 1 )’2( 1 )2( 1 AO x k AO Q AOx k AO Q xd k x QE 3.

Формулы для кажущегося сопротивления идеальной градиент-установки. MNEU I E AO I MNE MN ANAM I MNE k I U k k 22 2 212 11 ‘2 11 AO xk k )1(121 2 kk 212 23 ‘2 11 AO xk k : MNB: 212 11 ‘2 11 AO xk k )1(121 2 kk 2 12 2 3 ‘2 1 1 AO x k k

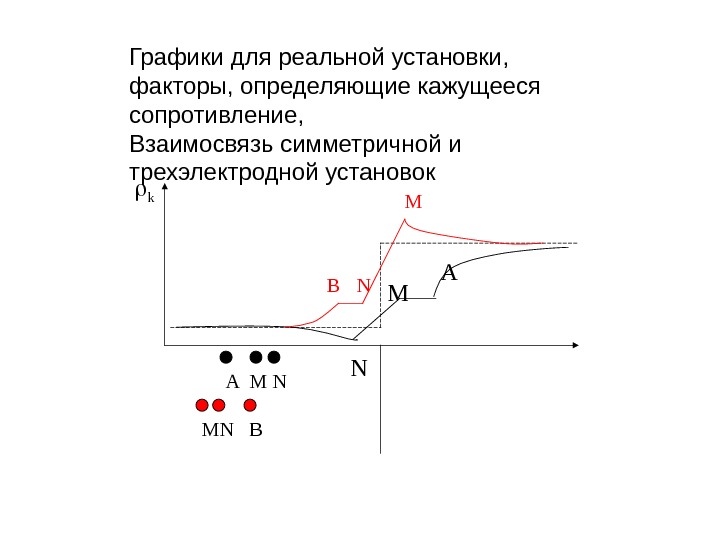
k MN B N M A A M N B N MГрафики для реальной установки, факторы, определяющие кажущееся сопротивление, Взаимосвязь симметричной и трехэлектродной установок

3. 2. 2. Сфера в электрическом поле Постановка задачи : ), ( 4)1 1 r. U RI UUU aan 0 sin 111 )2 2 aa. U rr U r rr )()()3 21 a. Ua )(1 )3 2 2 1 1 a r. U б rr. U a , 0), ()4 cos 222 rddr. RM A r d a 2 1 R U U Разрыв радиальной компоненты E ( при неразрывности тангенциальной)

Положим, что)()(), (Wr. Vr. U a 0 sin 2 WV r r W 0 sin 11 2 W Wr V r r. V m. W W sin 1 m r V r r. V 21 * ** cosz z. WW sin zz z sin 0 sin 2 m. W z 0)1( 2 m. W z z Уравнение Лежандра. Используем метод разделения переменных :

0)1( 2 m. W z z. Уравнение Лежандра имеет нетривиальные решения при : )1( nnm 0)1()1( 2 Wnn z W z z Решения уравнения – полиномы Лежандра, определяемые по формуле Родрига : n nn nn z dz d nz. P 1 !2 1 )( 2 1)(0 z. P cos)(1 zz. P )1)2 cos(3( 4 1 )(2 z. P )(cos nnn. Pc. W -частные решения Вернемся к уравнению ** )1(1 2 nn r. V r r. V 0)1(2 n. Vn r. V r r

Ему удовлетворяют решения : 1)2()1(1 ; nnn n r Vr. V Частное решение : 1)2()1( 1 nnn nn rbrb. V Объединяем решения : )(cos 1 ), ( 1 1)2()1( n nnn na P r. Br. A Pc rbrbr. U Общее решение : 0 1)(cos 1 ), ( n nnn n na. P r Br. Ar. U 0: n. Aar 0: n. Bar RI r. U 4), ( 1 0 1 )(cos 1 n n nn P r. B 0 )(cos n n. Pr. A ar ar

0)(cos 10 1 n n nnn n. P a Ba. A 01 1 nnn n a. Ba. A cos 21 44 2211 rddr. I RI Для rd: )(cos 11 0 nn n. P r d r. R Для окрестностей шара : r<d ), ( r. U 0 11 1 )(cos 1 4 n nnnn n P r. B d r. I 0 11)(cos 4 n nn n Pr. A d r. I ), (r r U 0 21 1 1)(cos 1 4 n nnnn n P r n B d rn. I 0 1 11 1)(cos 4 n nn Prn. A d rn. I )()()3 21 a. Ua )(1 )3 2 2 1 1 a r. U б Предварительно представим 1 /R с помощью полиномов Лежандра

3 б)0)(cos )1( 4 11 0 1 2 2 1 1 21 n nn n Pa. A n a Bn d an. I Решение уравнений 3 а и 3 б : 12 12 )1( )( nn n k n — коэффициент отражения 11 4 n n n d k. I A 1 12 1 4 n n d ak. I B RI r. U 4), ( 1 0 11 12 )(cos 1 n nnn n n. P rd ak 0 1)(cos n n n. Pr d k ar ar 4 1 I

Частный случай однородного поля : M A r d a 2 1 R M r d a 2 1 d>>r r/d<>a a/d<<1 RI r. U 4), ( 1 0 1 12 )(cos n nn n n. P dr ak 0 1)(cos n n n. Pr d k ar ar 4 1 I R A→

RI r. U 4), ( 1 cos 1 222 3 12 12 rd a cos 2 2 12 12 d r ar ar 4 1 I 12 12 12 k Rd RI r. U 4), ( 1 cos 22 3 12 12 r a ar ar 2 1 4 R I cos 212 12 r Ограничимся первым членом ряда, т. к. d – большая величина cos 244), ( 12 12 211 RI RI r. U 2 3 r a r ar ar

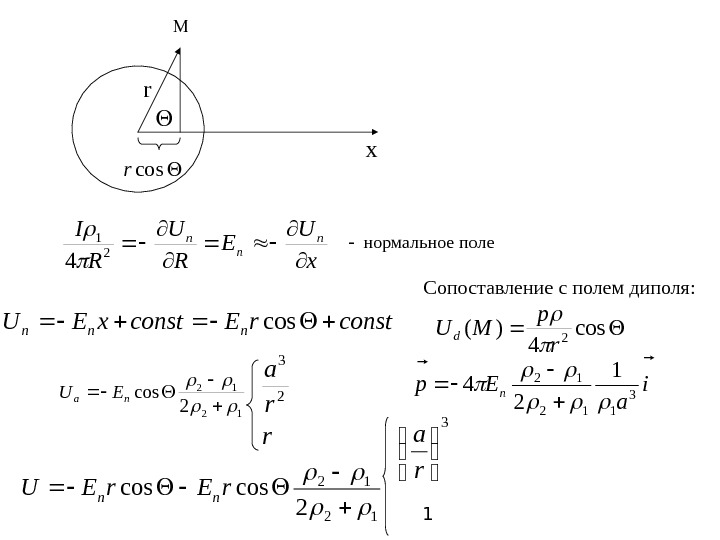
r xx U E R U R In n n 2 1 4 constr. Econstx. EU nnn cosr 12 12 2 cos na. EU r r a 2 3 Сопоставление с полем диполя : cos 4 )(2 r p MUd i a. Ep n 3 112 12 1 24 12 12 2 coscos r. EU nn 3 ra нормальное поле

Выводы : • Сферическое включение в однородном поле эквивалентно электрическому диполю, помещенному в центре сферы. • Физическими источниками аномального поля являются индуцированные источники, расположенные на поверхности включения. • Для шар-проводника внутреннее поле направлено как нормальное поле, для шара-изолятора – направлено противоположно нормальному полю.

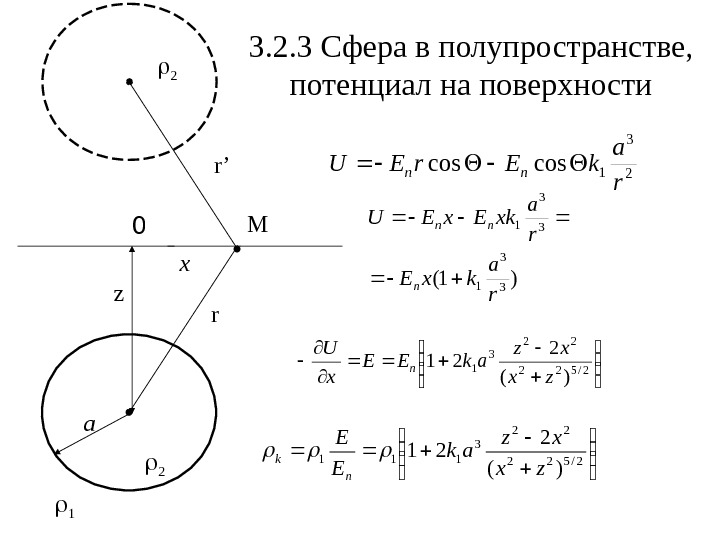
3. 2. 3 Сфера в полупространстве , потенциал на поверхности M r a 2 1 2 r’ z x 2 3 1 coscos ra k. Er. EU nn )1(3 3 1 r a kx. E r a xk. Ex. EU n nn 2/522 22 3 1 )( 2 21 zx xz ak. EE x. U n 2/522 22 3 111 )( 2 21 zx xz ak E E n k