2_Math_Foundation.ppt
- Количество слайдов: 132
 2. Математические основы Островец 1
2. Математические основы Островец 1
 2. Математические основы § 2. 1. Сигнал и его представление. § 2. 2. Необходимые математические понятия. § 2. 3. Ортогональные многочлены. § 2. 4. Разложение сигнала в ортогональный ряд. § 2. 5. Ортогональное представление в широкополосной сети. § 2. 6. Пример OFDM с тремя сигналами.
2. Математические основы § 2. 1. Сигнал и его представление. § 2. 2. Необходимые математические понятия. § 2. 3. Ортогональные многочлены. § 2. 4. Разложение сигнала в ортогональный ряд. § 2. 5. Ортогональное представление в широкополосной сети. § 2. 6. Пример OFDM с тремя сигналами.
 2. 1. Сигнал и его представление § Понятие «сигнал» применяется в различных смыслах. Так, сигналом называют физический процесс передачи информации во времени и пространстве с некоторым физическим носителем – электрическим током, электромагнитным полем, лучом света, звуком и т. д. Здесь на несущий сигнал накладываются данные. Примеры: радио -, телевизионная передача, стеганографическая передача данных, телефон, светофор, жесты регулировщика движения, матрос-сигнальщик с флажками, крик о помощи, звонок к началу занятий.
2. 1. Сигнал и его представление § Понятие «сигнал» применяется в различных смыслах. Так, сигналом называют физический процесс передачи информации во времени и пространстве с некоторым физическим носителем – электрическим током, электромагнитным полем, лучом света, звуком и т. д. Здесь на несущий сигнал накладываются данные. Примеры: радио -, телевизионная передача, стеганографическая передача данных, телефон, светофор, жесты регулировщика движения, матрос-сигнальщик с флажками, крик о помощи, звонок к началу занятий.
 2. 1. Сигнал и его представление § Мы рассматриваем сигнал x(t) как функцию от времени t на конечном промежутке времени (в общем случае на бесконечном интервале). Физически значением функции может быть напряжение, сила тока, и пр. § Если рассматривать x(t) как напряжение в цепи, то сила тока i(t) в цепи по закону Ома равна § Тогда мгновенная мощность (энергия) сигнала x(t) в момент t равна
2. 1. Сигнал и его представление § Мы рассматриваем сигнал x(t) как функцию от времени t на конечном промежутке времени (в общем случае на бесконечном интервале). Физически значением функции может быть напряжение, сила тока, и пр. § Если рассматривать x(t) как напряжение в цепи, то сила тока i(t) в цепи по закону Ома равна § Тогда мгновенная мощность (энергия) сигнала x(t) в момент t равна
 2. 1. Сигнал и его представление § Если считать, что сопротивление цепи постоянно, то энергия сигнала в момент t пропорциональна квадрату его величины, а если положить R=1, то энергия равна § Тогда энергия (работа) сигнала x(t) на интервале времени [t 1, t 2] будет равна § Это энергия (работа), которую затрачивает устройство, передающее сигнал x(t) в течение интервале времени [t 1, t 2].
2. 1. Сигнал и его представление § Если считать, что сопротивление цепи постоянно, то энергия сигнала в момент t пропорциональна квадрату его величины, а если положить R=1, то энергия равна § Тогда энергия (работа) сигнала x(t) на интервале времени [t 1, t 2] будет равна § Это энергия (работа), которую затрачивает устройство, передающее сигнал x(t) в течение интервале времени [t 1, t 2].
 2. 1. Сигнал и его представление § Для вещественных чисел, для точек в пространстве и для векторов известна мера близости объектов (абсолютная величина, длина, расстояние, норма). Известно понятие нормы (длины) вектора, которая приводит к понятию нормы сигнала. § Будем исходить из векторов в двумерном пространстве, но все результаты легко обобщаются на конечномерные пространства. Пусть вектор задан своими координатами. § Евклидовой нормой вектора A называется вещественное число
2. 1. Сигнал и его представление § Для вещественных чисел, для точек в пространстве и для векторов известна мера близости объектов (абсолютная величина, длина, расстояние, норма). Известно понятие нормы (длины) вектора, которая приводит к понятию нормы сигнала. § Будем исходить из векторов в двумерном пространстве, но все результаты легко обобщаются на конечномерные пространства. Пусть вектор задан своими координатами. § Евклидовой нормой вектора A называется вещественное число
 2. 1. Сигнал и его представление § (Существуют другие определения нормы, неевклидовы). § Расстояние r между векторами определяется как норма их разности, если A B r(A, B) Норма сигнала определяется аналогично.
2. 1. Сигнал и его представление § (Существуют другие определения нормы, неевклидовы). § Расстояние r между векторами определяется как норма их разности, если A B r(A, B) Норма сигнала определяется аналогично.
 2. 1. Сигнал и его представление § Пусть сигнала x(t) задан на интервале времени Нормой сигнала x(t) называется вещественное число § (при условии, что интеграл существует). § Пример. Найти норму затухающего осциллятора § На интервалах времени 1) параметры T=2, ω0=2π. , 2) , заданы .
2. 1. Сигнал и его представление § Пусть сигнала x(t) задан на интервале времени Нормой сигнала x(t) называется вещественное число § (при условии, что интеграл существует). § Пример. Найти норму затухающего осциллятора § На интервалах времени 1) параметры T=2, ω0=2π. , 2) , заданы .
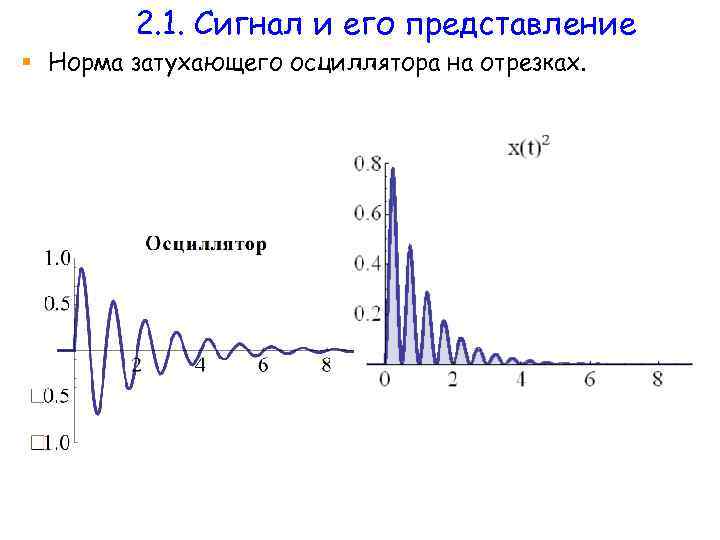 2. 1. Сигнал и его представление § Норма затухающего осциллятора на отрезках.
2. 1. Сигнал и его представление § Норма затухающего осциллятора на отрезках.
 2. 1. Сигнал и его представление § Норма затухающего осциллятора. § Соответствующие интегралы
2. 1. Сигнал и его представление § Норма затухающего осциллятора. § Соответствующие интегралы
 2. 1. Сигнал и его представление § То есть, на отрезке сигнал практически равен нулю (но конкретный вывод зависит от поставленной задачи!). § Заметим, что норма сигнала на отрезке близка к энергии сигнала на этом отрезке (будет рассматриваться далее). § Расстояние между сигналами x(t) и y(t), заданными на , измеряется как при условии, что интеграл существует Page 11
2. 1. Сигнал и его представление § То есть, на отрезке сигнал практически равен нулю (но конкретный вывод зависит от поставленной задачи!). § Заметим, что норма сигнала на отрезке близка к энергии сигнала на этом отрезке (будет рассматриваться далее). § Расстояние между сигналами x(t) и y(t), заданными на , измеряется как при условии, что интеграл существует Page 11
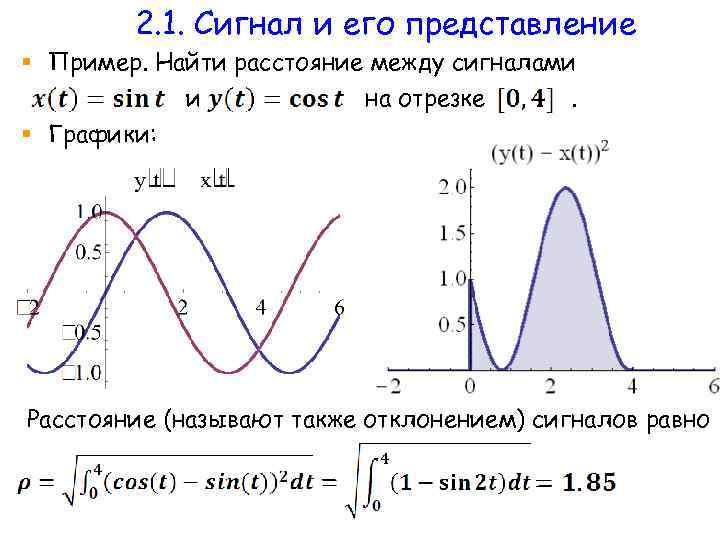 2. 1. Сигнал и его представление § Пример. Найти расстояние между сигналами и на отрезке. § Графики: Расстояние (называют также отклонением) сигналов равно
2. 1. Сигнал и его представление § Пример. Найти расстояние между сигналами и на отрезке. § Графики: Расстояние (называют также отклонением) сигналов равно
 2. 1. Сигнал и его представление § Наряду с нормой § (*) § существуют и другие определения нормы, например, Мы будем использовать только норму (*).
2. 1. Сигнал и его представление § Наряду с нормой § (*) § существуют и другие определения нормы, например, Мы будем использовать только норму (*).
 2. 1. Сигнал и его представление § Теперь рассмотрим два сигнал x(t) и y(t), заданных на промежутке времени. § Скалярным произведением сигналов x(t) и y(t) называется определенный интеграл § где s(t) – некоторая весовая функция. (Аналогично векторам можно найти и косинус угла между функциями !). § В функциональном анализе скалярное произведение функций x(t) и y(t) определяют в виде интеграла Page 14 где d. S(t) = s(t)dt.
2. 1. Сигнал и его представление § Теперь рассмотрим два сигнал x(t) и y(t), заданных на промежутке времени. § Скалярным произведением сигналов x(t) и y(t) называется определенный интеграл § где s(t) – некоторая весовая функция. (Аналогично векторам можно найти и косинус угла между функциями !). § В функциональном анализе скалярное произведение функций x(t) и y(t) определяют в виде интеграла Page 14 где d. S(t) = s(t)dt.
 2. 1. Сигнал и его представление § Понятно, что рассматриваемый определенный интеграл должен существовать. Весовой функцией s(t) может служить функция с некоторыми специальными свойствами. § В качестве s(t) можно использовать функцию плотности распределения некоторой непрерывной случайной величины, тогда S(t) - функция распределения этой величины. §В некоторых случаях s(t) =1, тогда S(t) =t, d S(t) =dt, то есть весовая функция в этих случаях просто отсутствует. §Норма сигнала x(t) равна корню квадратному из скалярного произведения сигнала с самим собой
2. 1. Сигнал и его представление § Понятно, что рассматриваемый определенный интеграл должен существовать. Весовой функцией s(t) может служить функция с некоторыми специальными свойствами. § В качестве s(t) можно использовать функцию плотности распределения некоторой непрерывной случайной величины, тогда S(t) - функция распределения этой величины. §В некоторых случаях s(t) =1, тогда S(t) =t, d S(t) =dt, то есть весовая функция в этих случаях просто отсутствует. §Норма сигнала x(t) равна корню квадратному из скалярного произведения сигнала с самим собой
 2. 1. Сигнал и его представление § Норма комплекснозначного сигнала x(t) – это корень квадратный из скалярного произведения с сопряженным сигналом § Сигналы x(t) и y(t) называются ортогональными, если их скалярное произведение равно нулю.
2. 1. Сигнал и его представление § Норма комплекснозначного сигнала x(t) – это корень квадратный из скалярного произведения с сопряженным сигналом § Сигналы x(t) и y(t) называются ортогональными, если их скалярное произведение равно нулю.
 2. 1. Сигнал и его представление § Пример. Проверить ортогональность сигналов § с весовой функцией s(t) = 1 на отрезке t ϵ [-T/2, T/2] § T=2π/ω, где m, n – целые числа. § Найдем скалярное произведение .
2. 1. Сигнал и его представление § Пример. Проверить ортогональность сигналов § с весовой функцией s(t) = 1 на отрезке t ϵ [-T/2, T/2] § T=2π/ω, где m, n – целые числа. § Найдем скалярное произведение .
 2. 1. Сигнал и его представление § При n ≠ m § При n = m
2. 1. Сигнал и его представление § При n ≠ m § При n = m
 2. 1. Сигнал и его представление § Сигнал x(t) не обязательно зависит от времени, аргумент t может быть любой природы. Можно обобщить понятие сигнала на многомерный случай. Так изображение размерности a на b можно задать как сигнал x(u, v), где а значение интенсивности x(u, v) лежит в интервале вещественных чисел от 0 до 255. На изображения переносятся определения нормы, расстояния и энергии. Переменные u и v, значения интенсивности могут быть дискретными, например, целыми числами; тогда получаем дискретное (цифровое) изображение.
2. 1. Сигнал и его представление § Сигнал x(t) не обязательно зависит от времени, аргумент t может быть любой природы. Можно обобщить понятие сигнала на многомерный случай. Так изображение размерности a на b можно задать как сигнал x(u, v), где а значение интенсивности x(u, v) лежит в интервале вещественных чисел от 0 до 255. На изображения переносятся определения нормы, расстояния и энергии. Переменные u и v, значения интенсивности могут быть дискретными, например, целыми числами; тогда получаем дискретное (цифровое) изображение.
 2. 2. Необходимые математическиепонятия § Для объяснения и обоснования понятий и результатов теории сигналов необходимо элементарное знание математики. § Тригонометрические функции. § В радиоэлектронике в основном используются сигналы, происходящие от колебаний. Периодические колебания хорошо описываются функциями синус и косинус. § Функция sin(t) периодическая, ограниченная, определена для любого значения аргумента t. § Периодом функции f(t) называется минимальное неотрицательное число T, такое, что для любого t
2. 2. Необходимые математическиепонятия § Для объяснения и обоснования понятий и результатов теории сигналов необходимо элементарное знание математики. § Тригонометрические функции. § В радиоэлектронике в основном используются сигналы, происходящие от колебаний. Периодические колебания хорошо описываются функциями синус и косинус. § Функция sin(t) периодическая, ограниченная, определена для любого значения аргумента t. § Периодом функции f(t) называется минимальное неотрицательное число T, такое, что для любого t
 2. 2. Необходимые математическиепонятия § Функция sin(t) имеет период T = 2 , если аргумент t это время, выраженное в секундах, то через 2 секунд функция начнет повторять свои значение, начнется новое колебание. Тогда частота колебаний функции sin(t) равна Hz (колебаний в секунду) § Можно выражать частоту колебаний величиной изменения угла в единицу времени. Угол измеряется в радианах, функция sin(t) за время T = 2 секунд выполнит полный оборот, то есть пройдет угол 2 радиан, тогда угловая скорость равна (радиан в секунду)
2. 2. Необходимые математическиепонятия § Функция sin(t) имеет период T = 2 , если аргумент t это время, выраженное в секундах, то через 2 секунд функция начнет повторять свои значение, начнется новое колебание. Тогда частота колебаний функции sin(t) равна Hz (колебаний в секунду) § Можно выражать частоту колебаний величиной изменения угла в единицу времени. Угол измеряется в радианах, функция sin(t) за время T = 2 секунд выполнит полный оборот, то есть пройдет угол 2 радиан, тогда угловая скорость равна (радиан в секунду)
 2. 2. Необходимые математическиепонятия § В математическом анализе выводится формула Эйлера, выражающая функции sin(t) и cos(t) через комплексные числа. § Формула Эйлера § Отсюда, взяв угол с положительным и отрицательным знаком, получаем значения sin(t) и cos(t).
2. 2. Необходимые математическиепонятия § В математическом анализе выводится формула Эйлера, выражающая функции sin(t) и cos(t) через комплексные числа. § Формула Эйлера § Отсюда, взяв угол с положительным и отрицательным знаком, получаем значения sin(t) и cos(t).
 2. 2. Необходимые математическиепонятия § В дальнейшем нам понадобится выражение для суммы в комплексной форме
2. 2. Необходимые математическиепонятия § В дальнейшем нам понадобится выражение для суммы в комплексной форме
 2. 2. Необходимые математическиепонятия § Понятие спектра сигнала. § Электрический сигнал sin(t) для передачи по проводам можно получить, равномерно вращая металлическую рамку в магнитном поле. При этом на концах рамки будет наблюдаться периодический электрический сигнал. Частота этого сигнала равна 1 (радиан в секунду) – это угловая скорость вращения рамки. Если параллельно соединить две вращающиеся рамки, то выходной сигнал будет получен смешиванием частот первого и второго сигнала. § Разумно предположить, что любой сигнал с некоторой погрешностью можно разложить в сумму функций sin(. ) и cos(. ) с определенными аргументами и амплитудами.
2. 2. Необходимые математическиепонятия § Понятие спектра сигнала. § Электрический сигнал sin(t) для передачи по проводам можно получить, равномерно вращая металлическую рамку в магнитном поле. При этом на концах рамки будет наблюдаться периодический электрический сигнал. Частота этого сигнала равна 1 (радиан в секунду) – это угловая скорость вращения рамки. Если параллельно соединить две вращающиеся рамки, то выходной сигнал будет получен смешиванием частот первого и второго сигнала. § Разумно предположить, что любой сигнал с некоторой погрешностью можно разложить в сумму функций sin(. ) и cos(. ) с определенными аргументами и амплитудами.
 2. 2. Необходимые математическиепонятия § Совокупность частот сигналов разложения дает спектр исходного сигнала. § Оценка определенных интегралов. § При анализе систем и сигналов иногда приходится вычислять определенные интегралы от сигналов различного вида. В редких случаях это бывают аналитически заданные сигналы с табличными интегралами. Чаще приходится оценивать интегралы от нетабличных функций. В этих случаях приходится применять приближенные численные методы. § Идея простейших приближенных методов оценки числового значения определенного интеграла состоит в замене интеграла суммой конечного числа слагаемых.
2. 2. Необходимые математическиепонятия § Совокупность частот сигналов разложения дает спектр исходного сигнала. § Оценка определенных интегралов. § При анализе систем и сигналов иногда приходится вычислять определенные интегралы от сигналов различного вида. В редких случаях это бывают аналитически заданные сигналы с табличными интегралами. Чаще приходится оценивать интегралы от нетабличных функций. В этих случаях приходится применять приближенные численные методы. § Идея простейших приближенных методов оценки числового значения определенного интеграла состоит в замене интеграла суммой конечного числа слагаемых.
 2. 2. Необходимые математическиепонятия § Из числа простейших распространены 3 метода: q 1) метод прямоугольников с тремя модификациями: значение левой точки отрезка; значение правой точки отрезка; значение середины отрезка; q 2) метод трапеций; q 3) метод Симпсона (метод парабол). § Применим метод прямоугольников к вычислению интеграла q Применим метод прямоугольников со значением левой точки отрезка деления.
2. 2. Необходимые математическиепонятия § Из числа простейших распространены 3 метода: q 1) метод прямоугольников с тремя модификациями: значение левой точки отрезка; значение правой точки отрезка; значение середины отрезка; q 2) метод трапеций; q 3) метод Симпсона (метод парабол). § Применим метод прямоугольников к вычислению интеграла q Применим метод прямоугольников со значением левой точки отрезка деления.
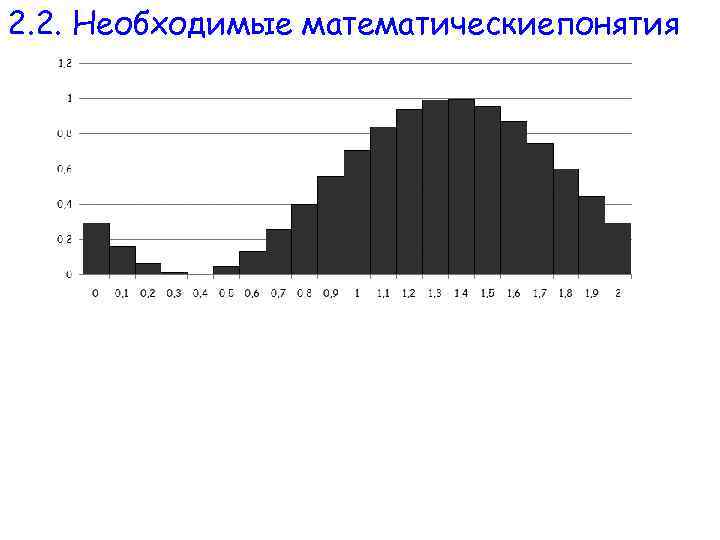
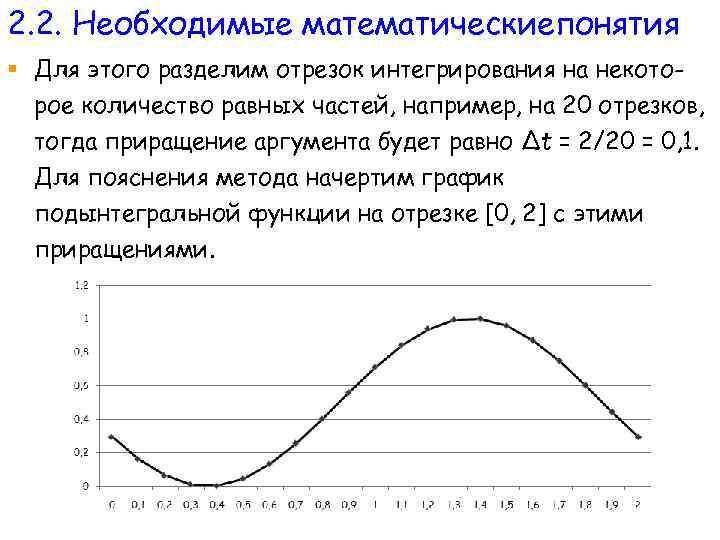 2. 2. Необходимые математическиепонятия § Для этого разделим отрезок интегрирования на некоторое количество равных частей, например, на 20 отрезков, тогда приращение аргумента будет равно ∆t = 2/20 = 0, 1. Для пояснения метода начертим график подынтегральной функции на отрезке [0, 2] с этими приращениями.
2. 2. Необходимые математическиепонятия § Для этого разделим отрезок интегрирования на некоторое количество равных частей, например, на 20 отрезков, тогда приращение аргумента будет равно ∆t = 2/20 = 0, 1. Для пояснения метода начертим график подынтегральной функции на отрезке [0, 2] с этими приращениями.
 2. 2. Необходимые математическиепонятия
2. 2. Необходимые математическиепонятия
 2. 2. Необходимые математическиепонятия § Вычислив точное значение интеграла по таблице интегрирования, получим истинное значение, I = 1. § Тогда абсолютная и относительная погрешности вычисления равны: § Если точное значение интеграла неизвестно, тогда воспользуемся правилом Рунге, возьмем, к примеру N 1 =20 и N 2=40 отрезков деления интервала. Приближения равны
2. 2. Необходимые математическиепонятия § Вычислив точное значение интеграла по таблице интегрирования, получим истинное значение, I = 1. § Тогда абсолютная и относительная погрешности вычисления равны: § Если точное значение интеграла неизвестно, тогда воспользуемся правилом Рунге, возьмем, к примеру N 1 =20 и N 2=40 отрезков деления интервала. Приближения равны
 2. 2. Необходимые математическиепонятия § Ортогональность функций. Система линейно независимых функций {f 0(t), f 1(t), . . . , fk(t), . . . }, заданных на некотором отрезке [a, b] называется ортогональной системой функций, если все они попарно ортогональны на этом отрезке. § Если все функции системы имеют норму 1, то система называется ортонормированной. § Пример ортогональной системы функций : § функции cos (kωt), k=0, 1, . . . ортогональны на отрезке [-π/ω, π/ω], но система не ортонормирована.
2. 2. Необходимые математическиепонятия § Ортогональность функций. Система линейно независимых функций {f 0(t), f 1(t), . . . , fk(t), . . . }, заданных на некотором отрезке [a, b] называется ортогональной системой функций, если все они попарно ортогональны на этом отрезке. § Если все функции системы имеют норму 1, то система называется ортонормированной. § Пример ортогональной системы функций : § функции cos (kωt), k=0, 1, . . . ортогональны на отрезке [-π/ω, π/ω], но система не ортонормирована.
 2. 2. Необходимые математическиепонятия § Функции Хаара. В 1909 г Альфред Хаар предложил систему кусочно-постоянных функций, которая стала широко применяться с 80 -х годов прошлого века для построения вейвлетов – интегральных преобразований, учитывающих временн. Ые интервалы передачи сигнала. § Для построения ортогональной системы Хаара вначале введем понятие диадических интервалов. § Для любой пары неотрицательных целых чисел j, k определим интервал I j, k такие интервалы, определенные для всех таких пар j, k называется семейством двоичных интервалов.
2. 2. Необходимые математическиепонятия § Функции Хаара. В 1909 г Альфред Хаар предложил систему кусочно-постоянных функций, которая стала широко применяться с 80 -х годов прошлого века для построения вейвлетов – интегральных преобразований, учитывающих временн. Ые интервалы передачи сигнала. § Для построения ортогональной системы Хаара вначале введем понятие диадических интервалов. § Для любой пары неотрицательных целых чисел j, k определим интервал I j, k такие интервалы, определенные для всех таких пар j, k называется семейством двоичных интервалов.
 2. 2. Необходимые математическиепонятия § Семейство двоичных интервалов имеет важные для дальнейших построений свойства. § Взаимное положение интервалов. Пусть j 0, k 0, j 1, k 1 – неотрицательные целые. Если , тогда справедливо одно и только одно из соотношений: либо § при этом в случаях b) и c) меньший интервал входит либо в левую, либо в правую половину большего.
2. 2. Необходимые математическиепонятия § Семейство двоичных интервалов имеет важные для дальнейших построений свойства. § Взаимное положение интервалов. Пусть j 0, k 0, j 1, k 1 – неотрицательные целые. Если , тогда справедливо одно и только одно из соотношений: либо § при этом в случаях b) и c) меньший интервал входит либо в левую, либо в правую половину большего.
 2. 2. Необходимые математическиепонятия § Если интервал Ij+1, k 0 входит в интервал Ij, k , то либо k 0=2 k (левая половина интервал Ij, k), либо k 0=2 k +1 (правая половина). § Для операций на двоичных интервалах введем оператор растяжения Da и оператор переноса Tb § По определению функции-индикатора множества
2. 2. Необходимые математическиепонятия § Если интервал Ij+1, k 0 входит в интервал Ij, k , то либо k 0=2 k (левая половина интервал Ij, k), либо k 0=2 k +1 (правая половина). § Для операций на двоичных интервалах введем оператор растяжения Da и оператор переноса Tb § По определению функции-индикатора множества
 2. 2. Необходимые математическиепонятия § Теперь определим вспомогательную функцию § Функции pj, k(t) называются весовыми функциями Хаара. Тогда очевидно, что
2. 2. Необходимые математическиепонятия § Теперь определим вспомогательную функцию § Функции pj, k(t) называются весовыми функциями Хаара. Тогда очевидно, что
 2. 2. Необходимые математическиепонятия § Функции Хаара, которые являются целью построения, получаются делением интервала-носителя функций pj, k() на две равные части, левую и правую, на левом подинтервале функция Хаара равна +1, на правом -1. § Ввиду знаков функций hj, k(t)
2. 2. Необходимые математическиепонятия § Функции Хаара, которые являются целью построения, получаются делением интервала-носителя функций pj, k() на две равные части, левую и правую, на левом подинтервале функция Хаара равна +1, на правом -1. § Ввиду знаков функций hj, k(t)
 2. 2. Необходимые математическиепонятия § Множество функций Хаара {h(t), hj, k() }, где j, k – пробегают все неотрицательные целые числа, называется ортогональной системой Хаара. Покажем, что функции, входящие в систему, попарно ортогональны. § Очевидно, что hj, k 0(t) и hj, k 1(t) при различных k 0 и k 1 имеют непересекающиеся носители, поэтому их произведение равно нулю и они ортогональны. § Если функции Хаара имеют разные индексы j, то положим для определенности j 0>j 1. Возможны 3 случая Взаимномного расположения интервалов (слайд 32). § Случай тогда носители функций не пересекаются и произведение равно нулю (то есть функции ортогональны).
2. 2. Необходимые математическиепонятия § Множество функций Хаара {h(t), hj, k() }, где j, k – пробегают все неотрицательные целые числа, называется ортогональной системой Хаара. Покажем, что функции, входящие в систему, попарно ортогональны. § Очевидно, что hj, k 0(t) и hj, k 1(t) при различных k 0 и k 1 имеют непересекающиеся носители, поэтому их произведение равно нулю и они ортогональны. § Если функции Хаара имеют разные индексы j, то положим для определенности j 0>j 1. Возможны 3 случая Взаимномного расположения интервалов (слайд 32). § Случай тогда носители функций не пересекаются и произведение равно нулю (то есть функции ортогональны).
 2. 2. Необходимые математическиепонятия § Случаи b) и c) - это когда один носитель входит в левую или правую половину другого, но и в той и в другой половине функция постоянна, то есть произведение сводится к интегралу на меньшем носителе, а он равен нулю (то есть и в этом случае функции ортогональны). § Таким образом, показано, что функции Хаара попарно ортогональны. § Функции Хаара широко применяются в приложениях, в частности, на основе этих функций построены вейвлеты Хаара.
2. 2. Необходимые математическиепонятия § Случаи b) и c) - это когда один носитель входит в левую или правую половину другого, но и в той и в другой половине функция постоянна, то есть произведение сводится к интегралу на меньшем носителе, а он равен нулю (то есть и в этом случае функции ортогональны). § Таким образом, показано, что функции Хаара попарно ортогональны. § Функции Хаара широко применяются в приложениях, в частности, на основе этих функций построены вейвлеты Хаара.
 2. 2. Необходимые математическиепонятия § Функции Уолша. Начнем изложение с исторически более ранних функций Радемахера. Эти функции r(k, t) (k – но -мер функции, t - аргумент) заданы на интервале [0, 1) для k=1, 2, … следующим образом: § Функции Радемахера попарно ортогональны, но система этих функций не полная, то есть не всякую ограниченную непрерывную функцию ( «хорошую» функцию) можно разложить по этим функциям.
2. 2. Необходимые математическиепонятия § Функции Уолша. Начнем изложение с исторически более ранних функций Радемахера. Эти функции r(k, t) (k – но -мер функции, t - аргумент) заданы на интервале [0, 1) для k=1, 2, … следующим образом: § Функции Радемахера попарно ортогональны, но система этих функций не полная, то есть не всякую ограниченную непрерывную функцию ( «хорошую» функцию) можно разложить по этим функциям.
 2. 2. Необходимые математическиепонятия Графики функций Радемахера для r(0, t) k = 0, 1, 2, 3. r(1, t) r(2, t) r(3, t)
2. 2. Необходимые математическиепонятия Графики функций Радемахера для r(0, t) k = 0, 1, 2, 3. r(1, t) r(2, t) r(3, t)
 2. 2. Необходимые математическиепонятия § Из функций Радемахера строятся функции Уолша. Существуют различные способы построения этих функций. Мы рассмотрим способ Пэли. § Функции Пэли pal(k, t) для k=1, 2, … строятся на основании двоичного представления номера k. Если k представляется двоичным разложением § То функция Пэли вычисляется по формуле
2. 2. Необходимые математическиепонятия § Из функций Радемахера строятся функции Уолша. Существуют различные способы построения этих функций. Мы рассмотрим способ Пэли. § Функции Пэли pal(k, t) для k=1, 2, … строятся на основании двоичного представления номера k. Если k представляется двоичным разложением § То функция Пэли вычисляется по формуле
 2. 2. Необходимые математическиепонятия § Нулевая функции Пэли pal(0, t) задается § Следующие функции Пэли вычисляется. Например, для k = 1, …, 6
2. 2. Необходимые математическиепонятия § Нулевая функции Пэли pal(0, t) задается § Следующие функции Пэли вычисляется. Например, для k = 1, …, 6
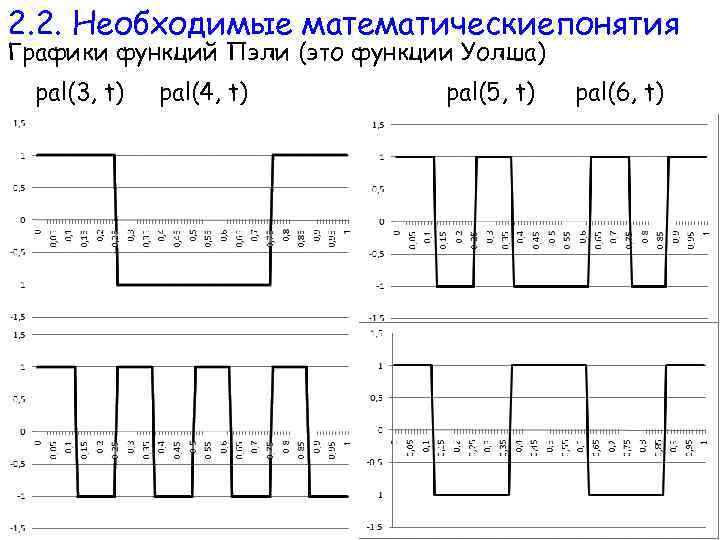 2. 2. Необходимые математическиепонятия Графики функций Пэли (это функции Уолша) pal(3, t) pal(4, t) pal(5, t) pal(6, t)
2. 2. Необходимые математическиепонятия Графики функций Пэли (это функции Уолша) pal(3, t) pal(4, t) pal(5, t) pal(6, t)
 2. 2. Необходимые математическиепонятия § Функции Уолша можно упорядочить по возрастанию частот функций. Это упорядочивание называется системой Хармута. Функции Уолша записываются в виде § В записи Хармута функции Уолша подобны базисным функциям § и очень похожи на базисным функциям Фурье, которые непрерывны.
2. 2. Необходимые математическиепонятия § Функции Уолша можно упорядочить по возрастанию частот функций. Это упорядочивание называется системой Хармута. Функции Уолша записываются в виде § В записи Хармута функции Уолша подобны базисным функциям § и очень похожи на базисным функциям Фурье, которые непрерывны.
 2. 2. Необходимые математическиепонятия § Ортогональное разложение. Одной из основных задач для ортогональных функций является задача разложения заданной функции в ряд по этому ортогональному базису. Такое разложение называется ортогональным разложением. § Пусть {P 0(t), P 1(t), … } – ортогональный базис в некотором пространстве функций. § Задача состоит в том, чтобы найти коэффициенты разложения функции y(t) в ряд § на интервале [a, b]. § Требуется найти коэффициенты разложения Ak по заданной функции y(t) и известным базисным функциям.
2. 2. Необходимые математическиепонятия § Ортогональное разложение. Одной из основных задач для ортогональных функций является задача разложения заданной функции в ряд по этому ортогональному базису. Такое разложение называется ортогональным разложением. § Пусть {P 0(t), P 1(t), … } – ортогональный базис в некотором пространстве функций. § Задача состоит в том, чтобы найти коэффициенты разложения функции y(t) в ряд § на интервале [a, b]. § Требуется найти коэффициенты разложения Ak по заданной функции y(t) и известным базисным функциям.
 2. 2. Необходимые математическиепонятия § Для того, чтобы найти Ak 0 для конкретного k 0, умножим обе части равенства на Pk 0(t) и на s(t) и на интервале ортогональности [a, b] проинтегрируем по t. § В предположении, что ряд сходится абсолютно и интегралы существуют, меняем порядок интегрирования
2. 2. Необходимые математическиепонятия § Для того, чтобы найти Ak 0 для конкретного k 0, умножим обе части равенства на Pk 0(t) и на s(t) и на интервале ортогональности [a, b] проинтегрируем по t. § В предположении, что ряд сходится абсолютно и интегралы существуют, меняем порядок интегрирования
 2. 2. Необходимые математическиепонятия § Ввиду ортогональности базисных функций Pk(t) все интегралы в правой части, кроме слагаемого с индексом k 0, обращаются в нули. Получаем: § Норму в квадрате § Обозначим через тогда
2. 2. Необходимые математическиепонятия § Ввиду ортогональности базисных функций Pk(t) все интегралы в правой части, кроме слагаемого с индексом k 0, обращаются в нули. Получаем: § Норму в квадрате § Обозначим через тогда
 2. 2. Необходимые математическиепонятия § Записывая для простоты результат с индексом k, получаем формулу § Так получаются и формулы разложения в ряд Фурье по базисным функциям sin(·) и cos(·) , и разложение по базисам Уолша и Хаара. § Мы не рассматриваем громоздкие вопросы о сходимости функциональных рядов и об их абсолютной сходимости. Эти важные вопросы рассматриваются в высшей математике, однако многие признаки сходимости основаны на сходимости геометрической прогрессии и не представляет большого труда досконально разобраться в них.
2. 2. Необходимые математическиепонятия § Записывая для простоты результат с индексом k, получаем формулу § Так получаются и формулы разложения в ряд Фурье по базисным функциям sin(·) и cos(·) , и разложение по базисам Уолша и Хаара. § Мы не рассматриваем громоздкие вопросы о сходимости функциональных рядов и об их абсолютной сходимости. Эти важные вопросы рассматриваются в высшей математике, однако многие признаки сходимости основаны на сходимости геометрической прогрессии и не представляет большого труда досконально разобраться в них.
 2. 2. Необходимые математическиепонятия § В реальных задачах интегрирование выполняется численными методами (метод прямоугольников, трапеций, Симпсона, для сильно осциллирующих функций метод Монте-Карло). Обычно при этом в явном виде используются пределы интегрирования a, b. Квадрирование несобственных интегралов также выполняется приближенно, для этого применяются более сложные методы.
2. 2. Необходимые математическиепонятия § В реальных задачах интегрирование выполняется численными методами (метод прямоугольников, трапеций, Симпсона, для сильно осциллирующих функций метод Монте-Карло). Обычно при этом в явном виде используются пределы интегрирования a, b. Квадрирование несобственных интегралов также выполняется приближенно, для этого применяются более сложные методы.
 2. 2. Необходимые математическиепонятия § Свертка. Это оператор в функциональном пространстве, который по двум исходным функциям интегральным преобразованием строит третью. § Оператор свертки применяется во многих приложениях функционального анализа. Его нельзя связывать только с теорией сигналов или с интегральными уравнениями, он используется во многих областях физики, радиоэлектроники и в др. науках. § Пример. Сигнал g(t) = sin(t) задан на интервале [1, 7]. Фильтр f(t) задан :
2. 2. Необходимые математическиепонятия § Свертка. Это оператор в функциональном пространстве, который по двум исходным функциям интегральным преобразованием строит третью. § Оператор свертки применяется во многих приложениях функционального анализа. Его нельзя связывать только с теорией сигналов или с интегральными уравнениями, он используется во многих областях физики, радиоэлектроники и в др. науках. § Пример. Сигнал g(t) = sin(t) задан на интервале [1, 7]. Фильтр f(t) задан :
 2. 2. Необходимые математическиепонятия § Подставляем сигналы в оператор свертки
2. 2. Необходимые математическиепонятия § Подставляем сигналы в оператор свертки
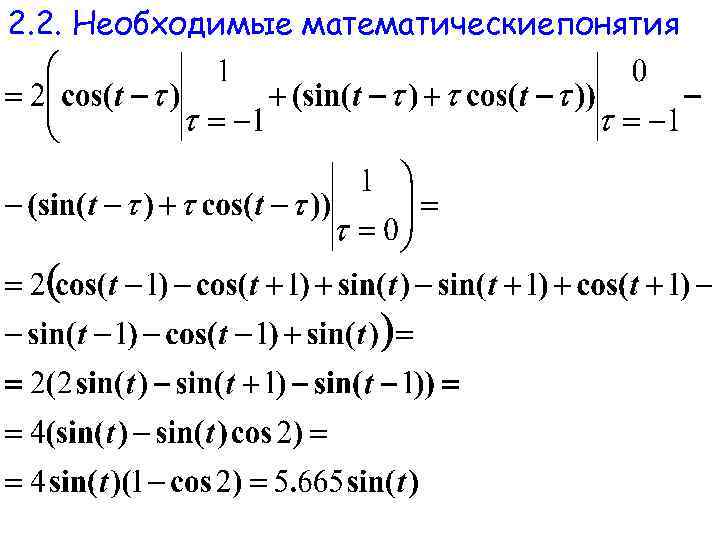 2. 2. Необходимые математическиепонятия
2. 2. Необходимые математическиепонятия
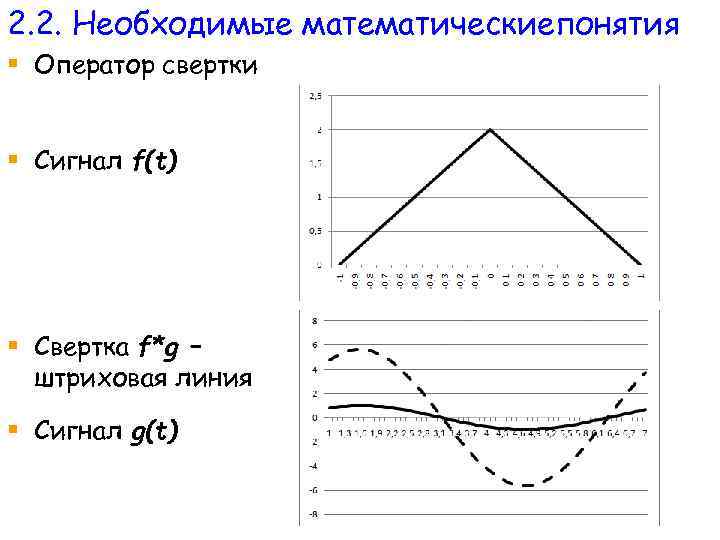 2. 2. Необходимые математическиепонятия § Оператор свертки § Сигнал f(t) § Свертка f*g – штриховая линия § Сигнал g(t)
2. 2. Необходимые математическиепонятия § Оператор свертки § Сигнал f(t) § Свертка f*g – штриховая линия § Сигнал g(t)
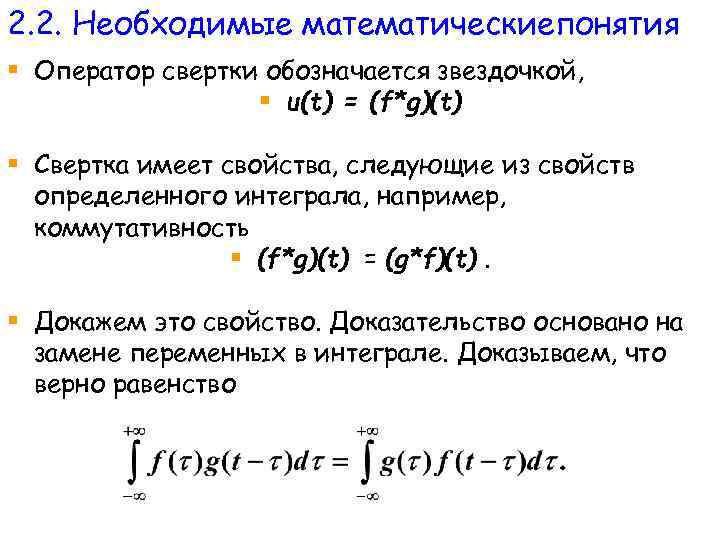 2. 2. Необходимые математическиепонятия § Оператор свертки обозначается звездочкой, § u(t) = (f*g)(t) § Свертка имеет свойства, следующие из свойств определенного интеграла, например, коммутативность § (f*g)(t) = (g*f)(t). § Докажем это свойство. Доказательство основано на замене переменных в интеграле. Доказываем, что верно равенство
2. 2. Необходимые математическиепонятия § Оператор свертки обозначается звездочкой, § u(t) = (f*g)(t) § Свертка имеет свойства, следующие из свойств определенного интеграла, например, коммутативность § (f*g)(t) = (g*f)(t). § Докажем это свойство. Доказательство основано на замене переменных в интеграле. Доказываем, что верно равенство
 2. 2. Необходимые математическиепонятия § Доказательство
2. 2. Необходимые математическиепонятия § Доказательство
 2. 2. Необходимые математическиепонятия § Итак, для функций были определены две операции, скалярное произведение (это вещественное число) и свертка (это свертка) § Функция f(. ) в операторе свертки называется ядром свертки. Но ввиду коммутативности функций, входящих в свертку это определение не совсем корректно.
2. 2. Необходимые математическиепонятия § Итак, для функций были определены две операции, скалярное произведение (это вещественное число) и свертка (это свертка) § Функция f(. ) в операторе свертки называется ядром свертки. Но ввиду коммутативности функций, входящих в свертку это определение не совсем корректно.
 2. 2. Необходимые математическиепонятия § Для дискретных сигналов также определяется скалярное произведение, как и для векторов, это сумма покомпонентных произведений – вещественное число. § На них можно перенести оператор свертки, интеграл для компонент вектора перейдет в сумму произведений, но это не покомпонентные произведения. § Пусть заданы сигнала, тогда их свертка – это новый дискретный сигнал
2. 2. Необходимые математическиепонятия § Для дискретных сигналов также определяется скалярное произведение, как и для векторов, это сумма покомпонентных произведений – вещественное число. § На них можно перенести оператор свертки, интеграл для компонент вектора перейдет в сумму произведений, но это не покомпонентные произведения. § Пусть заданы сигнала, тогда их свертка – это новый дискретный сигнал
 2. 2. Необходимые математическиепонятия § Если вернуться к векторам, то скалярное произведение – это сумма покомпонентных произведений – вещественное число. § На векторах можно определить и оператор свертки, интеграл от произведения компонент векторов перейдет в сумму произведений, но это не покомпонентные произведения. § Пусть заданы 2 вектора, тогда их свертка – это новый вектор
2. 2. Необходимые математическиепонятия § Если вернуться к векторам, то скалярное произведение – это сумма покомпонентных произведений – вещественное число. § На векторах можно определить и оператор свертки, интеграл от произведения компонент векторов перейдет в сумму произведений, но это не покомпонентные произведения. § Пусть заданы 2 вектора, тогда их свертка – это новый вектор
 2. 2. Необходимые математические понятия § Пример. Найти свертку векторов
2. 2. Необходимые математические понятия § Пример. Найти свертку векторов
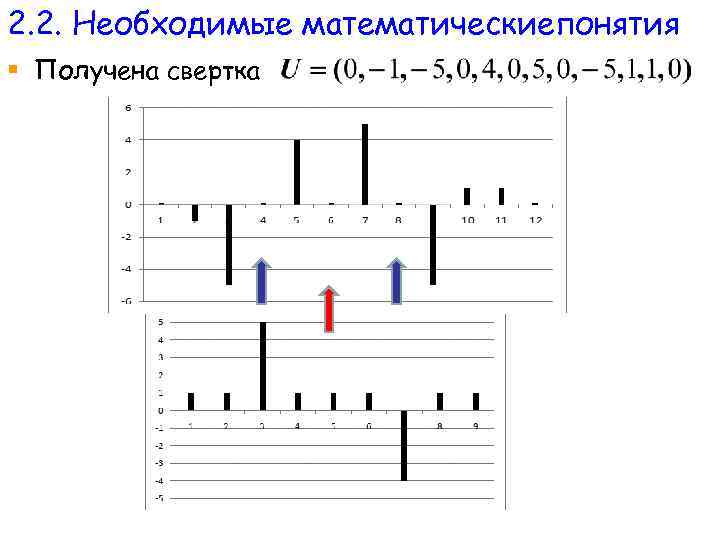 2. 2. Необходимые математическиепонятия § Получена свертка
2. 2. Необходимые математическиепонятия § Получена свертка
 2. 2. Необходимые математическиепонятия § Двумерная свертка. Фильтрацией называется преобразование объекта в области его определения с целью выделения в нем требуемых свойств. Преобразование фильтра не изменяет область определения объекта. § Примеры. 1. Кофейный фильтр выделяет в напитке жидкую компоненту, задерживая ненужный осадок. § 2. Вычисление производной непрерывного «гладкого» сигнала позволяет найти области его усиления и ослабления, то есть амплитуда сигнала либо увеличивается (производная больше нуля), либо уменьшается (производная меньше нуля). Фильтр-производная дает области усиления сигнала. § 2. Частотным фильтром сигнала можно подавлять сигнал в области вне заданного диапазона частот. § Рассмотрим фильтры, построенные на основе свертки, применяемые для обработки изображений.
2. 2. Необходимые математическиепонятия § Двумерная свертка. Фильтрацией называется преобразование объекта в области его определения с целью выделения в нем требуемых свойств. Преобразование фильтра не изменяет область определения объекта. § Примеры. 1. Кофейный фильтр выделяет в напитке жидкую компоненту, задерживая ненужный осадок. § 2. Вычисление производной непрерывного «гладкого» сигнала позволяет найти области его усиления и ослабления, то есть амплитуда сигнала либо увеличивается (производная больше нуля), либо уменьшается (производная меньше нуля). Фильтр-производная дает области усиления сигнала. § 2. Частотным фильтром сигнала можно подавлять сигнал в области вне заданного диапазона частот. § Рассмотрим фильтры, построенные на основе свертки, применяемые для обработки изображений.
 2. 2. Необходимые математическиепонятия § В общем виде свертка сигнала x(t) с ядром h(t) записывается в виде. Зануляя ядро h(t) вне заданного интервала [a, b], можно ограничиться вычислением свертки на интервале. Аналогично для двумерного изображения I, заданного функцией интенсивности I(x, y) свертку с двумерным ядром h(x, y) записывают как
2. 2. Необходимые математическиепонятия § В общем виде свертка сигнала x(t) с ядром h(t) записывается в виде. Зануляя ядро h(t) вне заданного интервала [a, b], можно ограничиться вычислением свертки на интервале. Аналогично для двумерного изображения I, заданного функцией интенсивности I(x, y) свертку с двумерным ядром h(x, y) записывают как
 2. 2. Необходимые математическиепонятия Если двумерное ядро H(x, y) оставить ненулевым только на квадрате -a, a] x [-a, a] , то свертка примет вид [ Это означает, что интенсивности I 0(x, y) будет определяться ядром и интенсивностью I(x, y) в пределах квадрата [x-a, x+a] x [y-a, y+a]. Это квадрат с «центром» в точке (x, y). В свертке (*) можно занулять ядро H(x, y) так, чтобы интегрирование велось по любой требуемой пользователю области D.
2. 2. Необходимые математическиепонятия Если двумерное ядро H(x, y) оставить ненулевым только на квадрате -a, a] x [-a, a] , то свертка примет вид [ Это означает, что интенсивности I 0(x, y) будет определяться ядром и интенсивностью I(x, y) в пределах квадрата [x-a, x+a] x [y-a, y+a]. Это квадрат с «центром» в точке (x, y). В свертке (*) можно занулять ядро H(x, y) так, чтобы интегрирование велось по любой требуемой пользователю области D.
 2. 2. Необходимые математические понятия Во многих случаях удобнее интегрировать по прямоугольнику или даже по квадрату, это уменьшает число машинных операций. Для цифрового изображения интегрирование выполняется на пикселях. Пиксель имеет ненулевые размеры, но если считать, что значение ядерной функции h(x, y) остается на пикселе постоянным (тогда можно брать ее значение в любой точке пикселя, лучше в центре), то свертка примет вид где (2 N+1)x(2 N+1) – размерность квадрата, на котором вычисляется свертка, - площадь пикселя.
2. 2. Необходимые математические понятия Во многих случаях удобнее интегрировать по прямоугольнику или даже по квадрату, это уменьшает число машинных операций. Для цифрового изображения интегрирование выполняется на пикселях. Пиксель имеет ненулевые размеры, но если считать, что значение ядерной функции h(x, y) остается на пикселе постоянным (тогда можно брать ее значение в любой точке пикселя, лучше в центре), то свертка примет вид где (2 N+1)x(2 N+1) – размерность квадрата, на котором вычисляется свертка, - площадь пикселя.
 2. 2. Необходимые математическиепонятия § Обычно считают, что площадь пикселя равна 1, это может изменять значение интеграла на постоянный множитель. Тогда вычисление свертки сводится к суммированию поэлементных произведений двух матриц, одна из них – матрица значений ядра на квадрате его определения, вторая матрица – это квадрат, вырезанный из картинки, элементы которого – значения интенсивности на соответствующих пикселях.
2. 2. Необходимые математическиепонятия § Обычно считают, что площадь пикселя равна 1, это может изменять значение интеграла на постоянный множитель. Тогда вычисление свертки сводится к суммированию поэлементных произведений двух матриц, одна из них – матрица значений ядра на квадрате его определения, вторая матрица – это квадрат, вырезанный из картинки, элементы которого – значения интенсивности на соответствующих пикселях.
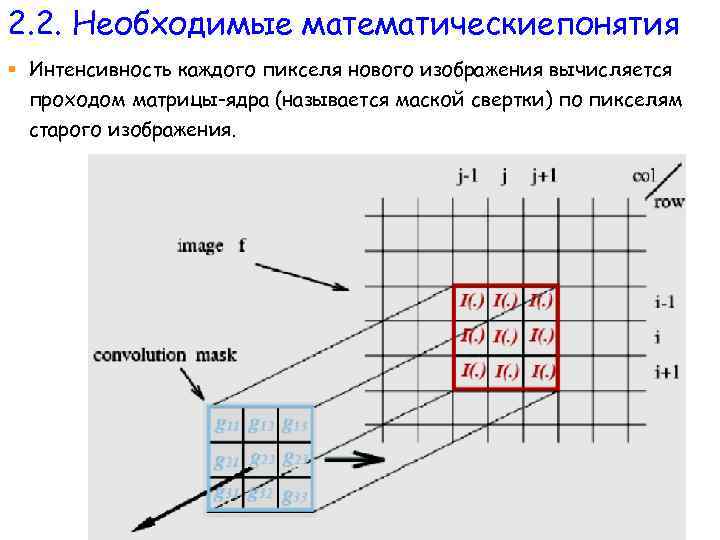 2. 2. Необходимые математическиепонятия § Интенсивность каждого пикселя нового изображения вычисляется проходом матрицы-ядра (называется маской свертки) по пикселям старого изображения.
2. 2. Необходимые математическиепонятия § Интенсивность каждого пикселя нового изображения вычисляется проходом матрицы-ядра (называется маской свертки) по пикселям старого изображения.
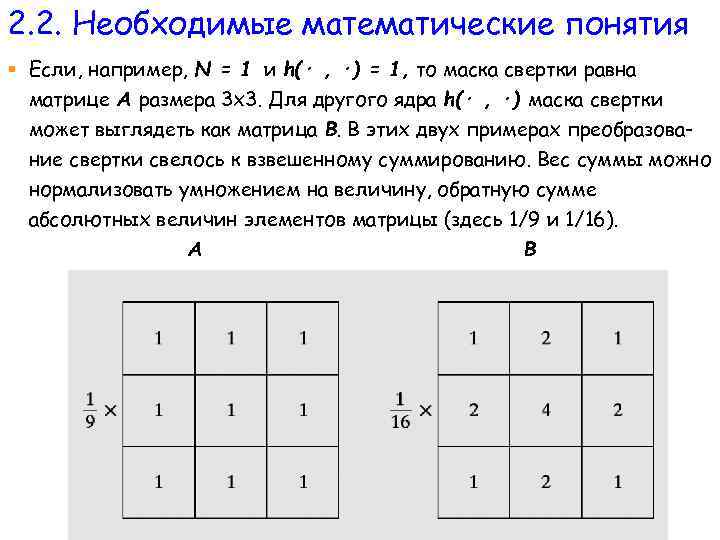 2. 2. Необходимые математические понятия § Если, например, N = 1 и h(· , ·) = 1, то маска свертки равна матрице А размера 3 х3. Для другого ядра h(· , ·) маска свертки может выглядеть как матрица В. В этих двух примерах преобразование свертки свелось к взвешенному суммированию. Вес суммы можно нормализовать умножением на величину, обратную сумме абсолютных величин элементов матрицы (здесь 1/9 и 1/16). А В
2. 2. Необходимые математические понятия § Если, например, N = 1 и h(· , ·) = 1, то маска свертки равна матрице А размера 3 х3. Для другого ядра h(· , ·) маска свертки может выглядеть как матрица В. В этих двух примерах преобразование свертки свелось к взвешенному суммированию. Вес суммы можно нормализовать умножением на величину, обратную сумме абсолютных величин элементов матрицы (здесь 1/9 и 1/16). А В
 2. 2. Необходимые математическиепонятия § Свертку применяют для построения разнообразных фильтров изображения. § Построим фильтр, сглаживающий рисунок. Обычно для этого применяется гауссиан. Это функция плотности стандартного нормального распределения (мат ожидание = 0, среднеквадратическое = ) параметр определяет «гладкость» графика функции, чем больше среднеквадратическое, тем более гладкий график.
2. 2. Необходимые математическиепонятия § Свертку применяют для построения разнообразных фильтров изображения. § Построим фильтр, сглаживающий рисунок. Обычно для этого применяется гауссиан. Это функция плотности стандартного нормального распределения (мат ожидание = 0, среднеквадратическое = ) параметр определяет «гладкость» графика функции, чем больше среднеквадратическое, тем более гладкий график.
 2. 2. Необходимые математические понятия § Гауссиан для двух аргументов равен произведению гауссианов. Для x и y можно брать разные среднеквадратические отклонения. Гауссиан для двух аргументов равен произведению гауссианов. Для цифровых изображений переходим к матрицам, при этом дискретизируем ядро, то есть заменяем гауссиан матрицей, элементы которой близки к числовым значениям гауссиана. Цифровое изображение дискретизировано изначально. Поскольку операции с целыми числами выполняются на компьютере во много раз быстрее, чем с плавающими, то при дискретизации желательно построить матрицу с целыми элементами, а затем после выполнения операции свертки нормализовать результат, т. е. разделить матрицу на сумму абсолютных величин матрицы-ядра.
2. 2. Необходимые математические понятия § Гауссиан для двух аргументов равен произведению гауссианов. Для x и y можно брать разные среднеквадратические отклонения. Гауссиан для двух аргументов равен произведению гауссианов. Для цифровых изображений переходим к матрицам, при этом дискретизируем ядро, то есть заменяем гауссиан матрицей, элементы которой близки к числовым значениям гауссиана. Цифровое изображение дискретизировано изначально. Поскольку операции с целыми числами выполняются на компьютере во много раз быстрее, чем с плавающими, то при дискретизации желательно построить матрицу с целыми элементами, а затем после выполнения операции свертки нормализовать результат, т. е. разделить матрицу на сумму абсолютных величин матрицы-ядра.
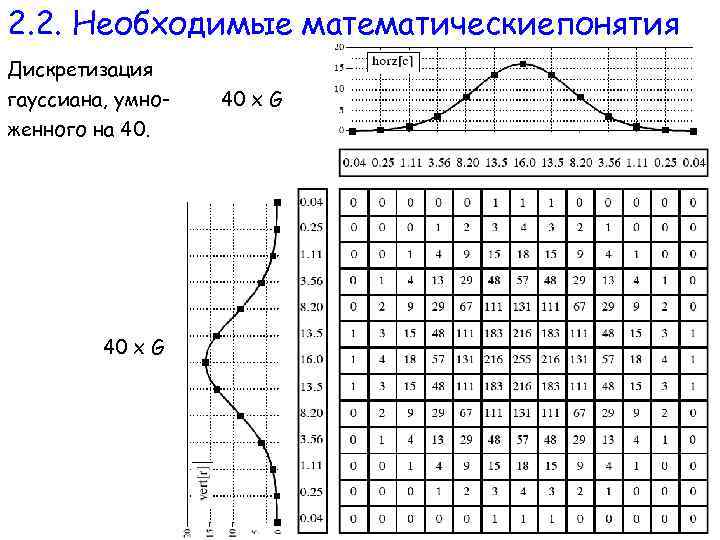 2. 2. Необходимые математическиепонятия Дискретизация гауссиана, умноженного на 40. 40 х G
2. 2. Необходимые математическиепонятия Дискретизация гауссиана, умноженного на 40. 40 х G
 2. 2. Необходимые математическиепонятия § Сглаживающий фильтр с гауссианом в качестве ядра свертки имеет вид полагают Экспонента с увеличением аргумента быстро затухает. В статистике существует правило «три сигма» : вероятность случайной величи-ны, имеющего стандартное нормальное распределение, близка к нулю на любом множестве вещественных чисел, не пересекающемся с интервалом То есть при единичном значении сигма можно считать, что гауссиан за пределами указанного интервала равен нулю (но это зависит от решаемой задачи). Тогда размер матрицы маски преобразования для N = 3 равен 7 х7.
2. 2. Необходимые математическиепонятия § Сглаживающий фильтр с гауссианом в качестве ядра свертки имеет вид полагают Экспонента с увеличением аргумента быстро затухает. В статистике существует правило «три сигма» : вероятность случайной величи-ны, имеющего стандартное нормальное распределение, близка к нулю на любом множестве вещественных чисел, не пересекающемся с интервалом То есть при единичном значении сигма можно считать, что гауссиан за пределами указанного интервала равен нулю (но это зависит от решаемой задачи). Тогда размер матрицы маски преобразования для N = 3 равен 7 х7.
 2. 2. Необходимые математические понятия § На самом деле для 2 D произведение экспонент даст еще м. Еньшую величину. То есть, число достаточно мало, его принимают за 0. Возьмем матрицу маски размера 5 х5. Получаем матрицу, умножим ее на 1000 округлим и нормализуем
2. 2. Необходимые математические понятия § На самом деле для 2 D произведение экспонент даст еще м. Еньшую величину. То есть, число достаточно мало, его принимают за 0. Возьмем матрицу маски размера 5 х5. Получаем матрицу, умножим ее на 1000 округлим и нормализуем
 2. 2. Необходимые математическиепонятия § Пример применения фильра Гаусса
2. 2. Необходимые математическиепонятия § Пример применения фильра Гаусса
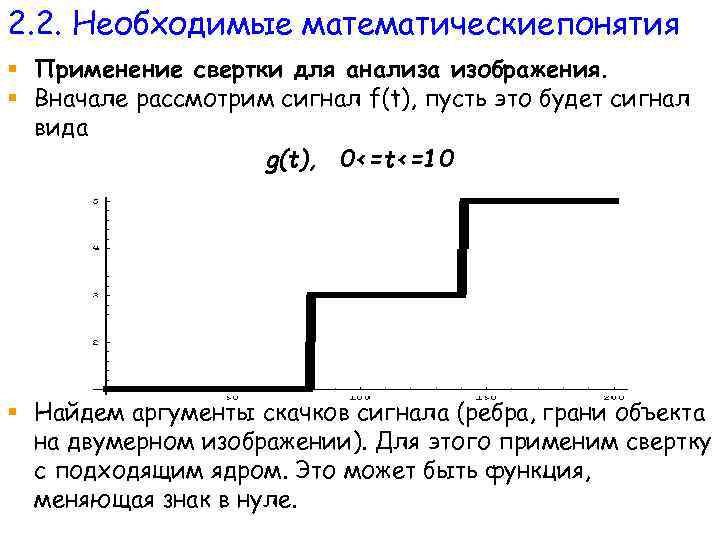 2. 2. Необходимые математическиепонятия § Применение свертки для анализа изображения. § Вначале рассмотрим сигнал f(t), пусть это будет сигнал вида g(t), 0<=t<=10 § Найдем аргументы скачков сигнала (ребра, грани объекта на двумерном изображении). Для этого применим свертку с подходящим ядром. Это может быть функция, меняющая знак в нуле.
2. 2. Необходимые математическиепонятия § Применение свертки для анализа изображения. § Вначале рассмотрим сигнал f(t), пусть это будет сигнал вида g(t), 0<=t<=10 § Найдем аргументы скачков сигнала (ребра, грани объекта на двумерном изображении). Для этого применим свертку с подходящим ядром. Это может быть функция, меняющая знак в нуле.
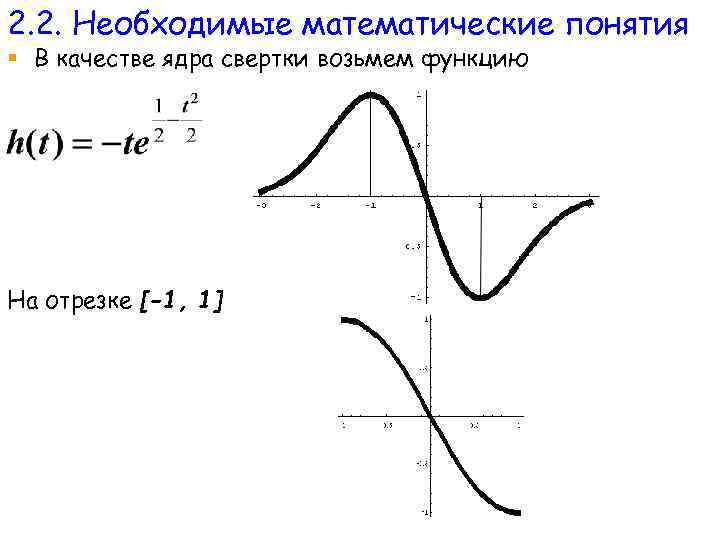 2. 2. Необходимые математические понятия § В качестве ядра свертки возьмем функцию На отрезке [-1, 1]
2. 2. Необходимые математические понятия § В качестве ядра свертки возьмем функцию На отрезке [-1, 1]
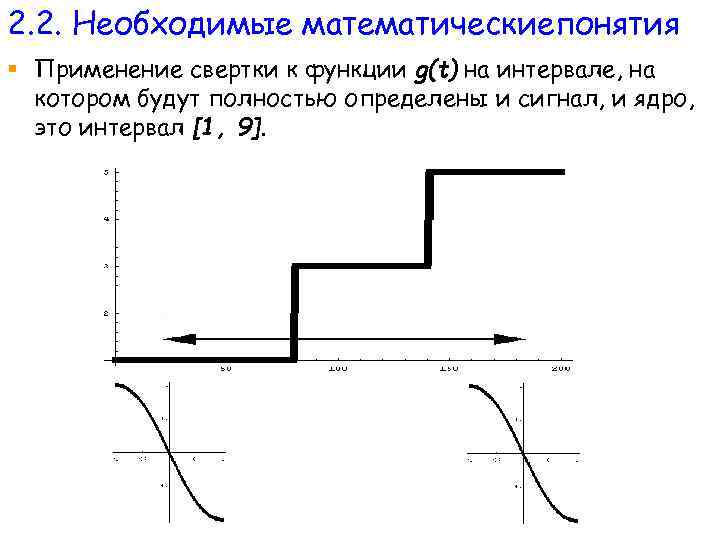 2. 2. Необходимые математическиепонятия § Применение свертки к функции g(t) на интервале, на котором будут полностью определены и сигнал, и ядро, это интервал [1, 9].
2. 2. Необходимые математическиепонятия § Применение свертки к функции g(t) на интервале, на котором будут полностью определены и сигнал, и ядро, это интервал [1, 9].
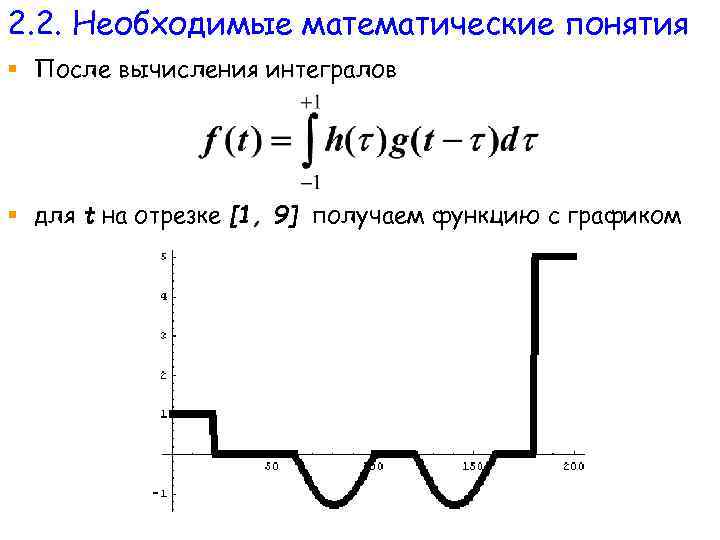 2. 2. Необходимые математические понятия § После вычисления интегралов § для t на отрезке [1, 9] получаем функцию с графиком
2. 2. Необходимые математические понятия § После вычисления интегралов § для t на отрезке [1, 9] получаем функцию с графиком
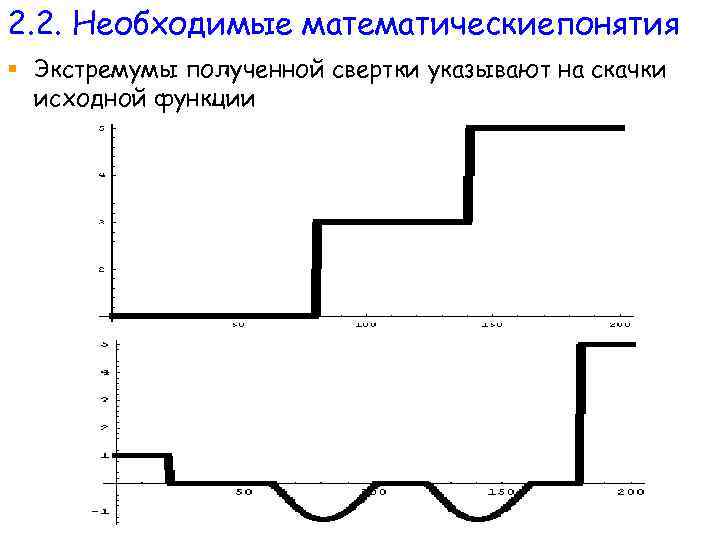 2. 2. Необходимые математическиепонятия § Экстремумы полученной свертки указывают на скачки исходной функции
2. 2. Необходимые математическиепонятия § Экстремумы полученной свертки указывают на скачки исходной функции
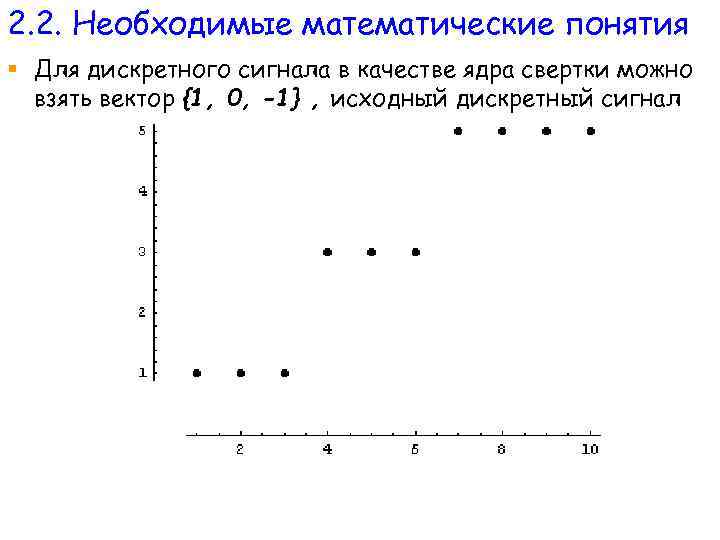 2. 2. Необходимые математические понятия § Для дискретного сигнала в качестве ядра свертки можно взять вектор {1, 0, -1} , исходный дискретный сигнал
2. 2. Необходимые математические понятия § Для дискретного сигнала в качестве ядра свертки можно взять вектор {1, 0, -1} , исходный дискретный сигнал
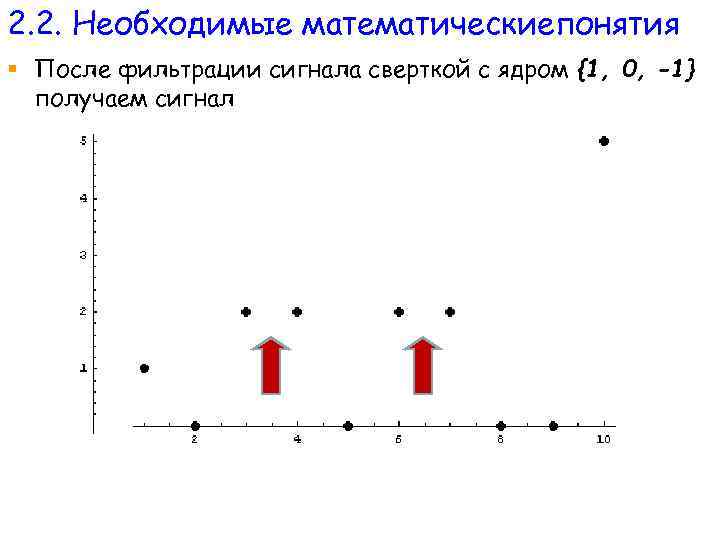 2. 2. Необходимые математическиепонятия § После фильтрации сигнала сверткой с ядром {1, 0, -1} получаем сигнал
2. 2. Необходимые математическиепонятия § После фильтрации сигнала сверткой с ядром {1, 0, -1} получаем сигнал
 2. 2. Необходимые математическиепонятия § Рассмотренный фильтр для выявления ребер был обобщем на двумерные сигналы. Для выявления вертикальных ребер (граней) дискретного двумерного сигнала было предложено ядро в виде матрицы § Собел предложил придать б. Ольший вес второй строке, для которой, собственно, и выделяется ребро. § Фильтр Собеля :
2. 2. Необходимые математическиепонятия § Рассмотренный фильтр для выявления ребер был обобщем на двумерные сигналы. Для выявления вертикальных ребер (граней) дискретного двумерного сигнала было предложено ядро в виде матрицы § Собел предложил придать б. Ольший вес второй строке, для которой, собственно, и выделяется ребро. § Фильтр Собеля :
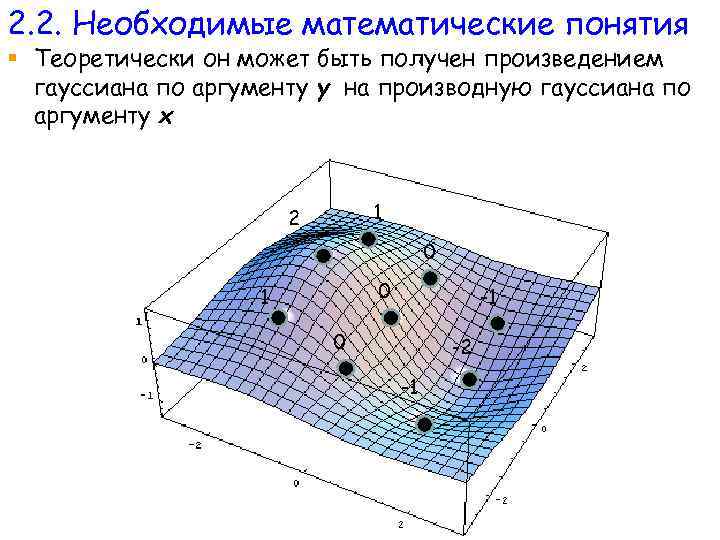 2. 2. Необходимые математические понятия § Теоретически он может быть получен произведением гауссиана по аргументу y на производную гауссиана по аргументу x 1 2 0 0 1 -1 0 -2 -1
2. 2. Необходимые математические понятия § Теоретически он может быть получен произведением гауссиана по аргументу y на производную гауссиана по аргументу x 1 2 0 0 1 -1 0 -2 -1
 2. 2. Необходимые математическиепонятия § Применение вертикального фильтра Собеля
2. 2. Необходимые математическиепонятия § Применение вертикального фильтра Собеля
 2. 2. Необходимые математические понятия § Преобразование аналогового сигнала в цифровой. На физическом уровне электрические сигналы как в проводной, так и в бепроводной сети передаются и принимаются в аналоговом виде (непрерывные сигналы). § Рассмотрим вопросы преобразование аналогового сигнала в цифровой (дискретный) и обратно, преобразование цифрового сигнала в аналоговый.
2. 2. Необходимые математические понятия § Преобразование аналогового сигнала в цифровой. На физическом уровне электрические сигналы как в проводной, так и в бепроводной сети передаются и принимаются в аналоговом виде (непрерывные сигналы). § Рассмотрим вопросы преобразование аналогового сигнала в цифровой (дискретный) и обратно, преобразование цифрового сигнала в аналоговый.
 2. 2. Необходимые математические понятия § Дискретный сигнал генерируется (или выбирается из аналогового) в последовательные равноотстоящие моменты времени 0, T, 2 T, 3 T, …. § Величина T > 0 называется интервалом дискретизации. § Квантование сигнала похоже на дискретизацию, только данная процедура производится не по времени, а по амплитуда сигнала x(t). Выбирается набор возможных значение сигнала X 0, X 1, . . . , Xk, . . . и значение x(t 0) округляется до ближайшего числа из этого набора. § Мы будем рассматривать и дискретизацию, и квантование. 84
2. 2. Необходимые математические понятия § Дискретный сигнал генерируется (или выбирается из аналогового) в последовательные равноотстоящие моменты времени 0, T, 2 T, 3 T, …. § Величина T > 0 называется интервалом дискретизации. § Квантование сигнала похоже на дискретизацию, только данная процедура производится не по времени, а по амплитуда сигнала x(t). Выбирается набор возможных значение сигнала X 0, X 1, . . . , Xk, . . . и значение x(t 0) округляется до ближайшего числа из этого набора. § Мы будем рассматривать и дискретизацию, и квантование. 84
 2. 2. Необходимые математические понятия § Квантование сигнала по значениям с постоянным шагом , начиная с нуля, выполняется достаточно просто. § Квантованное значение Xq(t 0) сигнала x(t 0) получается так: Например, если = 0. 1, то есть значения квантуются с шагом 0. 1, тогда число 0. 125 заменяется на: 85
2. 2. Необходимые математические понятия § Квантование сигнала по значениям с постоянным шагом , начиная с нуля, выполняется достаточно просто. § Квантованное значение Xq(t 0) сигнала x(t 0) получается так: Например, если = 0. 1, то есть значения квантуются с шагом 0. 1, тогда число 0. 125 заменяется на: 85
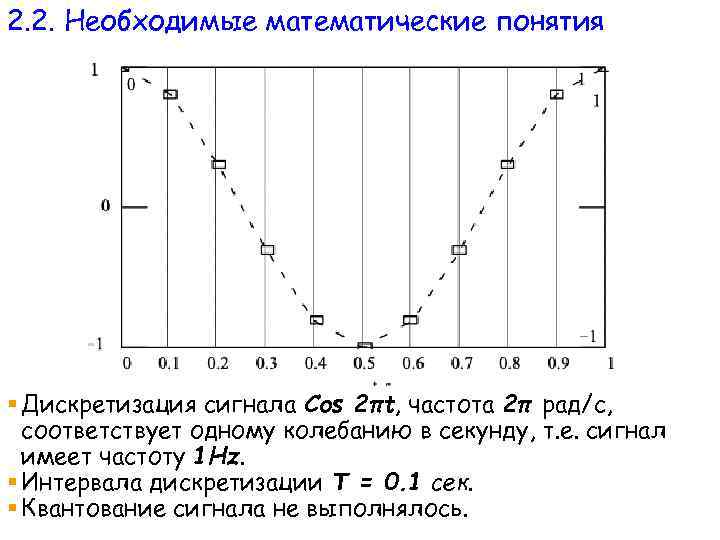 2. 2. Необходимые математические понятия § Дискретизация сигнала Cos 2πt, частота 2π рад/с, соответствует одному колебанию в секунду, т. е. сигнал имеет частоту 1 Hz. § Интервала дискретизации T = 0. 1 сек. § Квантование сигнала не выполнялось.
2. 2. Необходимые математические понятия § Дискретизация сигнала Cos 2πt, частота 2π рад/с, соответствует одному колебанию в секунду, т. е. сигнал имеет частоту 1 Hz. § Интервала дискретизации T = 0. 1 сек. § Квантование сигнала не выполнялось.
 2. 2. Необходимые математические понятия § Пример. Дискретизировать аналоговый сигнал с интервалом дискретизации T. Получаем значения При дискретизации с интервалом T, и одновременным квантованием с шагом 0. 2 получается сигнал Пример. Осциллятор при дискретизации с периодом T без квантования превращается в сигнал
2. 2. Необходимые математические понятия § Пример. Дискретизировать аналоговый сигнал с интервалом дискретизации T. Получаем значения При дискретизации с интервалом T, и одновременным квантованием с шагом 0. 2 получается сигнал Пример. Осциллятор при дискретизации с периодом T без квантования превращается в сигнал
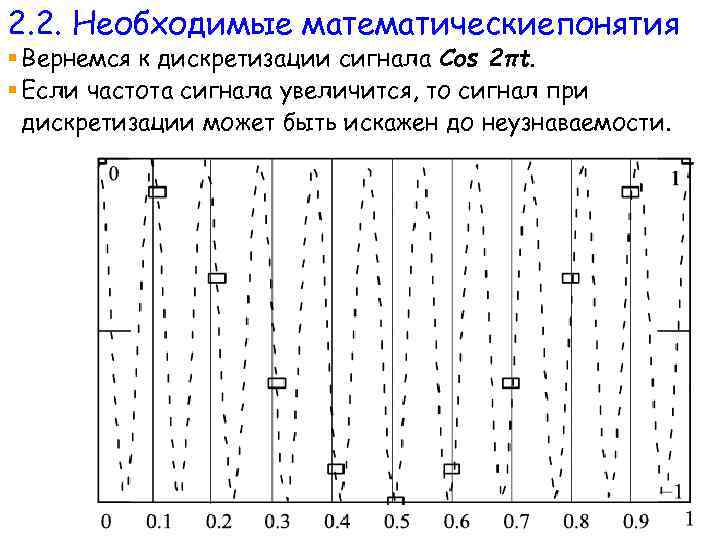 2. 2. Необходимые математическиепонятия § Вернемся к дискретизации сигнала Cos 2πt. § Если частота сигнала увеличится, то сигнал при дискретизации может быть искажен до неузнаваемости. 88
2. 2. Необходимые математическиепонятия § Вернемся к дискретизации сигнала Cos 2πt. § Если частота сигнала увеличится, то сигнал при дискретизации может быть искажен до неузнаваемости. 88
 2. 2. Необходимые математические понятия Проблему потери сигнала при дискретизации решает критерий Найквиста (Теорема Котельникова). Интервал дискретизации T должен быть в 2 или более раз меньше, чем период сигнала, который дискретизируется, то есть на периоде сигнала должно быть как минимум 2 точки дискретизации. Это то же самое, что частота дискретизации должна быть в 2 или более раз больше, чем частота сигнала, который дискретизируют. 89
2. 2. Необходимые математические понятия Проблему потери сигнала при дискретизации решает критерий Найквиста (Теорема Котельникова). Интервал дискретизации T должен быть в 2 или более раз меньше, чем период сигнала, который дискретизируется, то есть на периоде сигнала должно быть как минимум 2 точки дискретизации. Это то же самое, что частота дискретизации должна быть в 2 или более раз больше, чем частота сигнала, который дискретизируют. 89
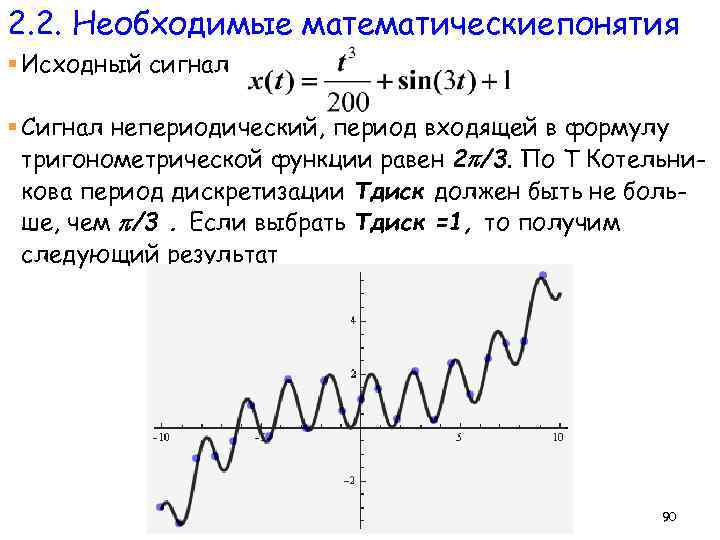 2. 2. Необходимые математическиепонятия § Исходный сигнал § Сигнал непериодический, период входящей в формулу тригонометрической функции равен 2 /3. По Т Котельникова период дискретизации Tдиск должен быть не больше, чем /3. Если выбрать Tдиск =1, то получим следующий результат 90
2. 2. Необходимые математическиепонятия § Исходный сигнал § Сигнал непериодический, период входящей в формулу тригонометрической функции равен 2 /3. По Т Котельникова период дискретизации Tдиск должен быть не больше, чем /3. Если выбрать Tдиск =1, то получим следующий результат 90
 2. 2. Необходимые математические понятия § Преобразование дискретного сигнала в аналоговый. На физическом уровне электромагнитные сигналы и передаваемые по проводникам, и беспроводные являются аналоговыми. Аналого-цифровой преобразователь § (АЦП) преобразуется «аналог в цифру» , а цифроаналоговый преобразователь (ЦАП) наоборот, «цифру в аналог» , это например, модемы и др. устройства. § Математическая модель для ЦАП использует специальную функцию sinc(. ) – функцию Ланцоша. Определение этой функции § В точке 0 функция sinc(. ) определяется по непрерывности, т. е. равна 1.
2. 2. Необходимые математические понятия § Преобразование дискретного сигнала в аналоговый. На физическом уровне электромагнитные сигналы и передаваемые по проводникам, и беспроводные являются аналоговыми. Аналого-цифровой преобразователь § (АЦП) преобразуется «аналог в цифру» , а цифроаналоговый преобразователь (ЦАП) наоборот, «цифру в аналог» , это например, модемы и др. устройства. § Математическая модель для ЦАП использует специальную функцию sinc(. ) – функцию Ланцоша. Определение этой функции § В точке 0 функция sinc(. ) определяется по непрерывности, т. е. равна 1.
 2. 2. Необходимые математические понятия § График sinc(. )
2. 2. Необходимые математические понятия § График sinc(. )
 2. 2. Необходимые математические понятия § Предполагая, что дискретный сигнал определен в равноотстоящих точках аргумента (они называются отсчетами), можно применить функцию Ланцоша. Дополнительное предположение: период построенного аналогового сигнала равен интервалу Tдиск между двумя последовательными отсчетами. § Интервалы между нулями функции Ланцоша, за исключением аргумента x=0, равны . Для того, чтобы интервалы между нулями функции были равны Tдиск , нужно сжать функцию:
2. 2. Необходимые математические понятия § Предполагая, что дискретный сигнал определен в равноотстоящих точках аргумента (они называются отсчетами), можно применить функцию Ланцоша. Дополнительное предположение: период построенного аналогового сигнала равен интервалу Tдиск между двумя последовательными отсчетами. § Интервалы между нулями функции Ланцоша, за исключением аргумента x=0, равны . Для того, чтобы интервалы между нулями функции были равны Tдиск , нужно сжать функцию:
 2. 2. Необходимые математические понятия § Теперь построим интерполяционных функцию, которая совпадает с дискретным сигналом в точках отсчета. Для примера рассмотрим 2 точки с аргументами t=0, t=Tдиск и интерполируем дискретный сигнал в этих точках отсчета аналоговым сигналом § В точках отсчета t=0, t=Tдиск сигнал S(t) и совпадает с дискретным сигналом, при других значениях t аналоговый сигнал определяется функцией Ланцоша. В общем случае аналоговый сигнал равен
2. 2. Необходимые математические понятия § Теперь построим интерполяционных функцию, которая совпадает с дискретным сигналом в точках отсчета. Для примера рассмотрим 2 точки с аргументами t=0, t=Tдиск и интерполируем дискретный сигнал в этих точках отсчета аналоговым сигналом § В точках отсчета t=0, t=Tдиск сигнал S(t) и совпадает с дискретным сигналом, при других значениях t аналоговый сигнал определяется функцией Ланцоша. В общем случае аналоговый сигнал равен
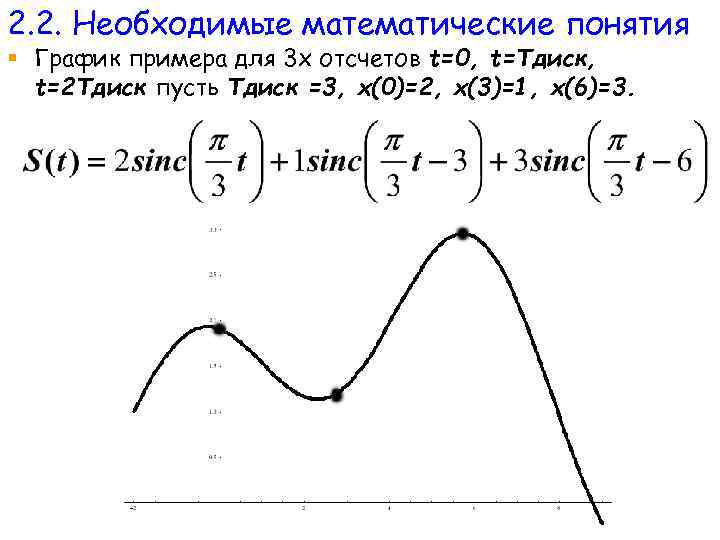 2. 2. Необходимые математические понятия § График примера для 3 х отсчетов t=0, t=Tдиск, t=2 Tдиск пусть Tдиск =3, x(0)=2, x(3)=1, x(6)=3.
2. 2. Необходимые математические понятия § График примера для 3 х отсчетов t=0, t=Tдиск, t=2 Tдиск пусть Tдиск =3, x(0)=2, x(3)=1, x(6)=3.
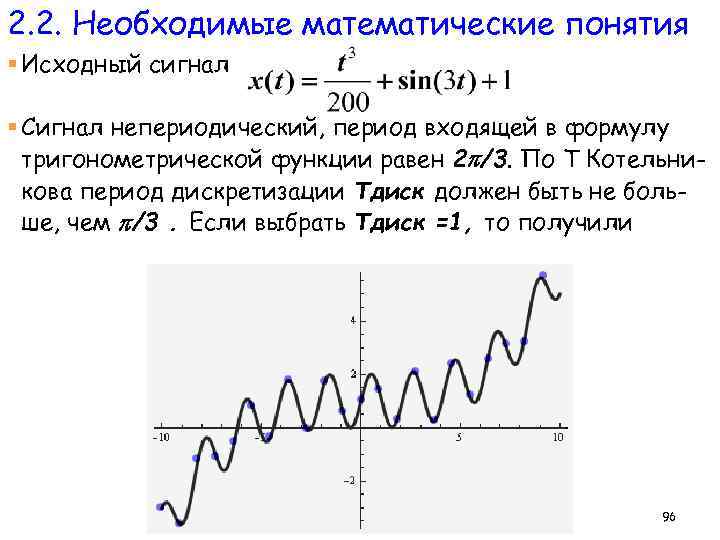 2. 2. Необходимые математические понятия § Исходный сигнал § Сигнал непериодический, период входящей в формулу тригонометрической функции равен 2 /3. По Т Котельникова период дискретизации Tдиск должен быть не больше, чем /3. Если выбрать Tдиск =1, то получили 96
2. 2. Необходимые математические понятия § Исходный сигнал § Сигнал непериодический, период входящей в формулу тригонометрической функции равен 2 /3. По Т Котельникова период дискретизации Tдиск должен быть не больше, чем /3. Если выбрать Tдиск =1, то получили 96
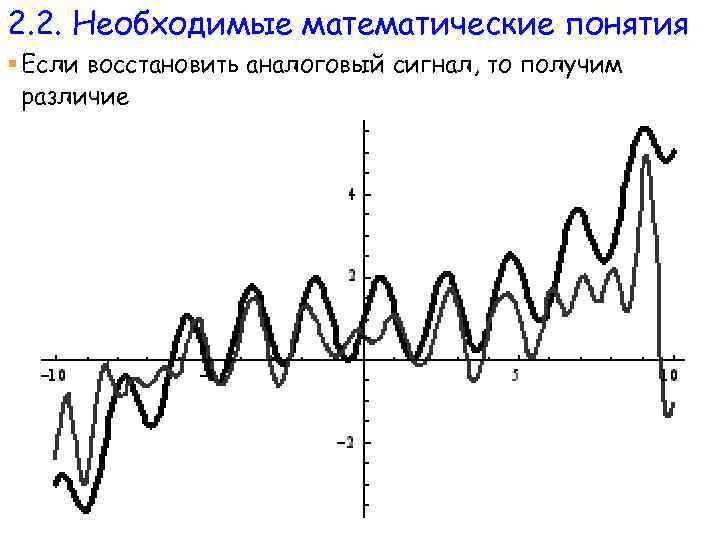 2. 2. Необходимые математические понятия § Если восстановить аналоговый сигнал, то получим различие
2. 2. Необходимые математические понятия § Если восстановить аналоговый сигнал, то получим различие
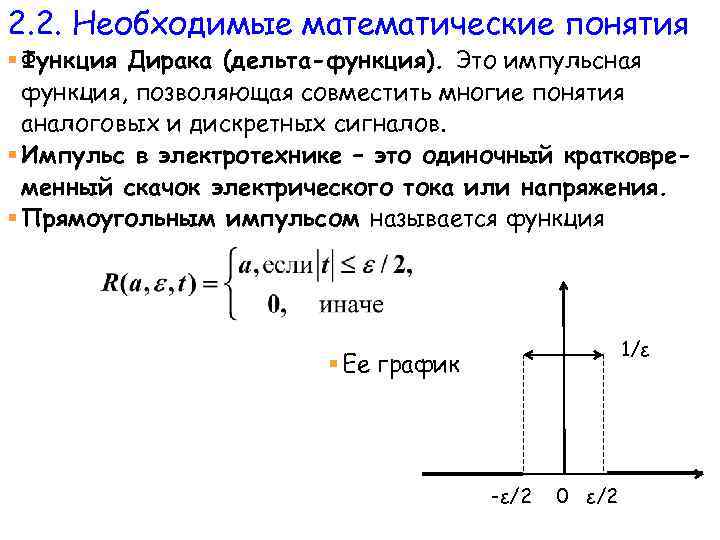 2. 2. Необходимые математические понятия § Функция Дирака (дельта-функция). Это импульсная функция, позволяющая совместить многие понятия аналоговых и дискретных сигналов. § Импульс в электротехнике – это одиночный кратковременный скачок электрического тока или напряжения. § Прямоугольным импульсом называется функция 1/ε § Ее график -ε/2 0 ε/2
2. 2. Необходимые математические понятия § Функция Дирака (дельта-функция). Это импульсная функция, позволяющая совместить многие понятия аналоговых и дискретных сигналов. § Импульс в электротехнике – это одиночный кратковременный скачок электрического тока или напряжения. § Прямоугольным импульсом называется функция 1/ε § Ее график -ε/2 0 ε/2
 2. 2. Необходимые математические понятия § Определенный интеграл от прямоугольного импульса по всей оси времени для любого ε > 0 равен 1: кроме того, предел 99
2. 2. Необходимые математические понятия § Определенный интеграл от прямоугольного импульса по всей оси времени для любого ε > 0 равен 1: кроме того, предел 99
 2. 2. Необходимые математические понятия Тогда подынтегральная функция выражения отлична от нуля только для значений аргумента -ε/2 < τ – t < ε/2 , то есть при t - ε/2 < τ < t + ε/2. На этом интервале импульс равен 1/ε, интеграл (1) принимает вид: 100
2. 2. Необходимые математические понятия Тогда подынтегральная функция выражения отлична от нуля только для значений аргумента -ε/2 < τ – t < ε/2 , то есть при t - ε/2 < τ < t + ε/2. На этом интервале импульс равен 1/ε, интеграл (1) принимает вид: 100
 2. 2. Необходимые математические понятия § По определению интеграла последнее выражение равно разности первообразных от функции h(t): § (H(t + ε/2) - H(t - ε/2))/ε. Последнее отношение в пределе – это производная от H(t) в точке t, то есть значение h(t). Таким образом, мы показали, что для любой точки t 0 из отрезка [0, M] (вне этого отрезка h(t)=0 ) выполняется равенство Приближенное равенство верно для малых ε. Это свойство импульса для оператора свертки.
2. 2. Необходимые математические понятия § По определению интеграла последнее выражение равно разности первообразных от функции h(t): § (H(t + ε/2) - H(t - ε/2))/ε. Последнее отношение в пределе – это производная от H(t) в точке t, то есть значение h(t). Таким образом, мы показали, что для любой точки t 0 из отрезка [0, M] (вне этого отрезка h(t)=0 ) выполняется равенство Приближенное равенство верно для малых ε. Это свойство импульса для оператора свертки.
 2. 2. Необходимые математические понятия Пример импульсного воздействия 102
2. 2. Необходимые математические понятия Пример импульсного воздействия 102
 2. 2. Необходимые математические понятия Пример импульсного воздействия 103
2. 2. Необходимые математические понятия Пример импульсного воздействия 103
 2. 2. Необходимые математические понятия § В 1930 году для решения задач теоретической физики английскому физику П. Дираку, одному из основателей квантовой механики, не хватило аппарата классической математики, и он ввел новый объект, названный “дельта -функцией”, который выходил за рамки классического определения функции. § П. Дирак определил дельта-функцию δ(x) следующим образом: 104
2. 2. Необходимые математические понятия § В 1930 году для решения задач теоретической физики английскому физику П. Дираку, одному из основателей квантовой механики, не хватило аппарата классической математики, и он ввел новый объект, названный “дельта -функцией”, который выходил за рамки классического определения функции. § П. Дирак определил дельта-функцию δ(x) следующим образом: 104
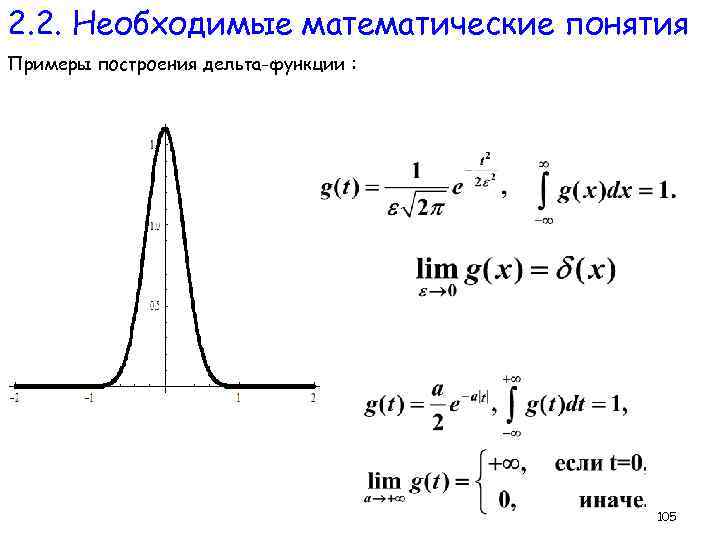 2. 2. Необходимые математические понятия Примеры построения дельта-функции : 105
2. 2. Необходимые математические понятия Примеры построения дельта-функции : 105
 2. 2. Необходимые математические понятия § δ-функция в реальных задачах моделируется удобным для исследователя способом, прямоугольным импульсом, треугольным импульсом, экспонентой (как на предыдущем слайде) и др. функциями. Эти и другие функции моделируют импульс и широко применяются в радиофизике. Параметры приближения выбираются в зависимости от решаемой задачи. § δ(x) не является функцией в обычном смысле, так как из этого определения следуют несовместимые условия с точки зрения классического определения функции и интеграла (то есть такая функция не существует). 106
2. 2. Необходимые математические понятия § δ-функция в реальных задачах моделируется удобным для исследователя способом, прямоугольным импульсом, треугольным импульсом, экспонентой (как на предыдущем слайде) и др. функциями. Эти и другие функции моделируют импульс и широко применяются в радиофизике. Параметры приближения выбираются в зависимости от решаемой задачи. § δ(x) не является функцией в обычном смысле, так как из этого определения следуют несовместимые условия с точки зрения классического определения функции и интеграла (то есть такая функция не существует). 106
 2. 2. Необходимые математические понятия § В частности, для свертки выполняется условие Упражнение. Определить треугольный импульс и найти его параметры. 107
2. 2. Необходимые математические понятия § В частности, для свертки выполняется условие Упражнение. Определить треугольный импульс и найти его параметры. 107
 2. 2. Необходимые математические понятия § Определим функцию единичного скачка, которая называется еще функцией Хевисайда: § Ee график 1 § 0 х 108
2. 2. Необходимые математические понятия § Определим функцию единичного скачка, которая называется еще функцией Хевисайда: § Ee график 1 § 0 х 108
 2. 2. Необходимые математические понятия § Производная функции Хевисайда существует и равна нулю во всех точках, кроме x=0. В этой точке предел отношения приращения функции и приращению аргумента уходит на бесконечность. Если построить последовательность кусочно-линейных функций вида, 109
2. 2. Необходимые математические понятия § Производная функции Хевисайда существует и равна нулю во всех точках, кроме x=0. В этой точке предел отношения приращения функции и приращению аргумента уходит на бесконечность. Если построить последовательность кусочно-линейных функций вида, 109
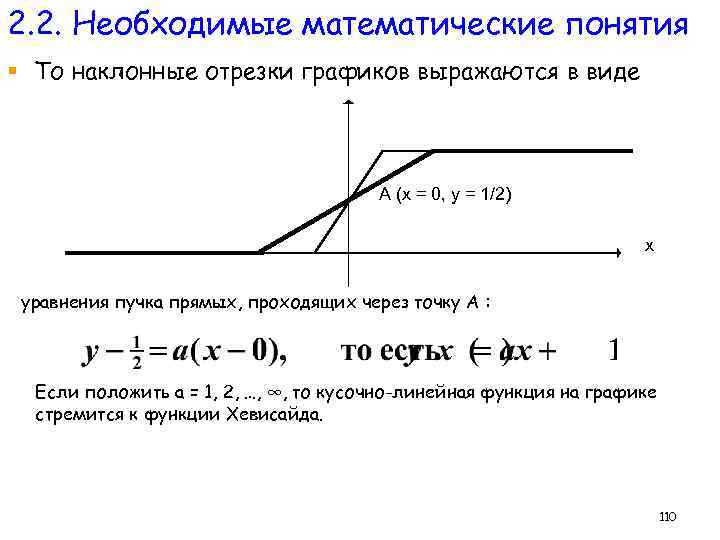 2. 2. Необходимые математические понятия § То наклонные отрезки графиков выражаются в виде A (x = 0, y = 1/2) x уравнения пучка прямых, проходящих через точку А : Если положить а = 1, 2, …, ∞, то кусочно-линейная функция на графике стремится к функции Хевисайда. 110
2. 2. Необходимые математические понятия § То наклонные отрезки графиков выражаются в виде A (x = 0, y = 1/2) x уравнения пучка прямых, проходящих через точку А : Если положить а = 1, 2, …, ∞, то кусочно-линейная функция на графике стремится к функции Хевисайда. 110
 2. 2. Необходимые математические понятия § Производные таких функций равны При а = 1, 2, … получается последовательность производных, совпадающих с прямоугольными функциями, при а ∞ они стремятся к δ-функции. То есть :
2. 2. Необходимые математические понятия § Производные таких функций равны При а = 1, 2, … получается последовательность производных, совпадающих с прямоугольными функциями, при а ∞ они стремятся к δ-функции. То есть :
 2. 2. Необходимые математические понятия Свойства δ-функции : 1. Фильтрация 2. Связь с функцией Хевисайда 3. Масштабирование 4. Четность 5. Дифференцирование
2. 2. Необходимые математические понятия Свойства δ-функции : 1. Фильтрация 2. Связь с функцией Хевисайда 3. Масштабирование 4. Четность 5. Дифференцирование
 2. 2. Необходимые математические понятия § § Доказательство свойств: 1. Доказано ранее, это импульсный метод идентификации. 2. Доказано ранее в этом пункте. 3. Пусть а > 0, докажем свойство для представления δ-функции как предела прямоугольной функции При умножении аргумента прямоугольной функции на a числовое значение интеграла изменится То есть, δ-функцию приближает Вторая часть определения δ-функции - предел очевидно выполняется.
2. 2. Необходимые математические понятия § § Доказательство свойств: 1. Доказано ранее, это импульсный метод идентификации. 2. Доказано ранее в этом пункте. 3. Пусть а > 0, докажем свойство для представления δ-функции как предела прямоугольной функции При умножении аргумента прямоугольной функции на a числовое значение интеграла изменится То есть, δ-функцию приближает Вторая часть определения δ-функции - предел очевидно выполняется.
 2. 2. Необходимые математические понятия § То есть при а > 0 В пределе очевидно выполняется. Если а < 0, то доказательство аналогично с учетом изменения знака интеграла.
2. 2. Необходимые математические понятия § То есть при а > 0 В пределе очевидно выполняется. Если а < 0, то доказательство аналогично с учетом изменения знака интеграла.
 2. 2. Необходимые математические понятия 4. Следует из свойства 3 при а = -1. 5. Продиффиренцируем обе части свойства 1 и применим свойство 4 (четность): Положим t=0 и получим требуемое свойство.
2. 2. Необходимые математические понятия 4. Следует из свойства 3 при а = -1. 5. Продиффиренцируем обе части свойства 1 и применим свойство 4 (четность): Положим t=0 и получим требуемое свойство.
 2. 2. Необходимые математические понятия § Дискретная дельта-функция. Для дискретных сигналов определяется аналог непрерывной - функции, обозначим ее 1(t). § Ее график 1 0
2. 2. Необходимые математические понятия § Дискретная дельта-функция. Для дискретных сигналов определяется аналог непрерывной - функции, обозначим ее 1(t). § Ее график 1 0
 2. 2. Необходимые математические понятия § Интегральное свойство необходимо и для 1(t). Для этого определяют 1(t) на интервале. § Дискретный сигнал x(t) с отсчетами k. T бывает удобно представить в виде суммы § Такая запись упрощает некоторые операции с сигналом, например, теперь легко записать дискретный сигнал на заданном интервале.
2. 2. Необходимые математические понятия § Интегральное свойство необходимо и для 1(t). Для этого определяют 1(t) на интервале. § Дискретный сигнал x(t) с отсчетами k. T бывает удобно представить в виде суммы § Такая запись упрощает некоторые операции с сигналом, например, теперь легко записать дискретный сигнал на заданном интервале.
 2. 2. Необходимые математические понятия § Дискретная функция Хевисайда, заданная на отсчетах k. T записывается как
2. 2. Необходимые математические понятия § Дискретная функция Хевисайда, заданная на отсчетах k. T записывается как
 2. 2. Необходимые математические понятия § Применение функции для дискретных случайных величин. Вначале рассмотрим пример дискретной случайной величины. § Пусть дискретная случайная величина X(ω) принимает и значения x 1 = -1, x 2 = 0, x 3 = 1, x 4 = 3 с вероятностями: 119
2. 2. Необходимые математические понятия § Применение функции для дискретных случайных величин. Вначале рассмотрим пример дискретной случайной величины. § Пусть дискретная случайная величина X(ω) принимает и значения x 1 = -1, x 2 = 0, x 3 = 1, x 4 = 3 с вероятностями: 119
 2. 2. Необходимые математические понятия § Функция распределения FX(x) дискретной случайной величины X(ω) по определению равна § FX(x) = P{X(ω) ≤ x}, § для нашего примера она равна
2. 2. Необходимые математические понятия § Функция распределения FX(x) дискретной случайной величины X(ω) по определению равна § FX(x) = P{X(ω) ≤ x}, § для нашего примера она равна
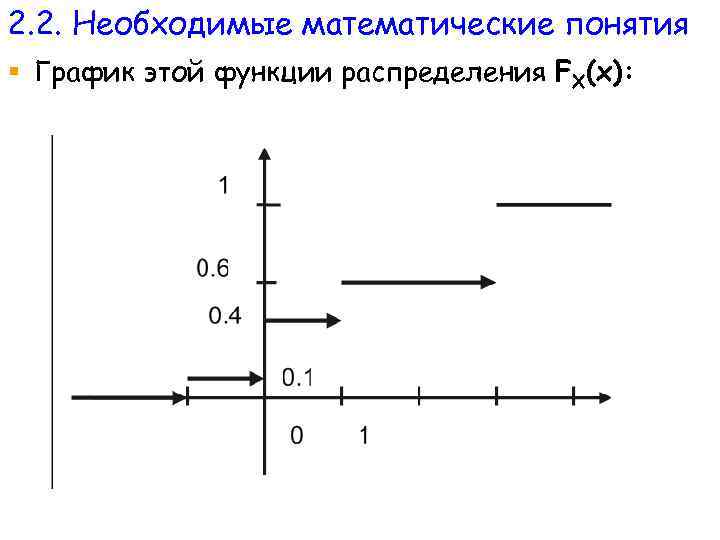 2. 2. Необходимые математические понятия § График этой функции распределения FX(x):
2. 2. Необходимые математические понятия § График этой функции распределения FX(x):
 2. 2. Необходимые математические понятия § Как известно из теории вероятностей, производной такой функция распределения FX(x) не существует, то есть случайная величина X(ω) не имеет функции плотности распределения p. X(x) = F′X(x). § Но применяя 1(x) и δ-функцию, можно построить функцию плотности распределения p. X(x) и для такой случайной величины X(ω). § Для построения функции плотности p. X(x) вначале построим функцию распределения FX(x) с использованием функции единичного скачка
2. 2. Необходимые математические понятия § Как известно из теории вероятностей, производной такой функция распределения FX(x) не существует, то есть случайная величина X(ω) не имеет функции плотности распределения p. X(x) = F′X(x). § Но применяя 1(x) и δ-функцию, можно построить функцию плотности распределения p. X(x) и для такой случайной величины X(ω). § Для построения функции плотности p. X(x) вначале построим функцию распределения FX(x) с использованием функции единичного скачка
 2. 2. Необходимые математические понятия § График функции § § а 1( x – c ) a 0 с х § Построенную функцию плотности FX(x) можно выразить через функцию единичного скачка 1(x). В точках разрыва функция распределения FX(x) увеличивается на скачок в точке разрыва, например, в точке x=-1 скачок равен 0. 1. Этот скачок можно выразить функцией Хевисайда с коэффициентом 0. 1. § 0. 1 1(x + 1)
2. 2. Необходимые математические понятия § График функции § § а 1( x – c ) a 0 с х § Построенную функцию плотности FX(x) можно выразить через функцию единичного скачка 1(x). В точках разрыва функция распределения FX(x) увеличивается на скачок в точке разрыва, например, в точке x=-1 скачок равен 0. 1. Этот скачок можно выразить функцией Хевисайда с коэффициентом 0. 1. § 0. 1 1(x + 1)
 2. 2. Необходимые математические понятия § Такую функцию плотности FX(x) можно выразить через функцию единичного скачка 1(x). В точках разрыва функция распределения FX(x) увеличивается на вероятность в точке разрыва, то выполняется скачок, например, в точке x=1 скачок равен 1/3. Этот скачок можно выразить функцией Хевисайда с коэффициентом 1/3. § - это скачок на 1/3 в точке x=1. § Наша функция FX(x) имеет три скачка, поэтому для ее выражения используем сумму трех функций Хевисайда.
2. 2. Необходимые математические понятия § Такую функцию плотности FX(x) можно выразить через функцию единичного скачка 1(x). В точках разрыва функция распределения FX(x) увеличивается на вероятность в точке разрыва, то выполняется скачок, например, в точке x=1 скачок равен 1/3. Этот скачок можно выразить функцией Хевисайда с коэффициентом 1/3. § - это скачок на 1/3 в точке x=1. § Наша функция FX(x) имеет три скачка, поэтому для ее выражения используем сумму трех функций Хевисайда.
 2. 2. Необходимые математические понятия § Наша функция FX(x) имеет 4 скачка, поэтому для ее выражения используем сумму 4 -х функций Хевисайда. § Функцию плотности FX(x) можно записать через функцию единичного скачка 1(x) и найти ее производную Такая функция p. X(x) удовлетворяет всем свойствам функции плотности.
2. 2. Необходимые математические понятия § Наша функция FX(x) имеет 4 скачка, поэтому для ее выражения используем сумму 4 -х функций Хевисайда. § Функцию плотности FX(x) можно записать через функцию единичного скачка 1(x) и найти ее производную Такая функция p. X(x) удовлетворяет всем свойствам функции плотности.
 2. 2. Необходимые математические понятия § Ортогональное представление в широкополосном диапазоне. Стандарт Wi-Fi представляет беспроводные локальные сети (WLAN), он зарегистрирован как стандарт IEEE 802. 11. Этот стандарт определяет эфирный интерфейс между беспроводным клиентом и базовой станцией или между двумя беспроводными клиентами. Стандарт IEEE 802. 11 имеет несколько версий: 802. 11 a, 802. 11 b, 802. 11 g, 802. 11 n и т. д, каждая из которых предполагает работу в нелицензируемых полосах частот. § Проблема состоит в том, что требуется обеспечить устойчивую связь с наибольшим числом абонентов на выделенном диапазоне. § Кратко рассмотрим один из методов использования широкополосного диапазона в стандартах Wi-Fi, это § метод ортогонального мультиплексирования OFDM § (Orthogonal Frequency Division Multiplexing).
2. 2. Необходимые математические понятия § Ортогональное представление в широкополосном диапазоне. Стандарт Wi-Fi представляет беспроводные локальные сети (WLAN), он зарегистрирован как стандарт IEEE 802. 11. Этот стандарт определяет эфирный интерфейс между беспроводным клиентом и базовой станцией или между двумя беспроводными клиентами. Стандарт IEEE 802. 11 имеет несколько версий: 802. 11 a, 802. 11 b, 802. 11 g, 802. 11 n и т. д, каждая из которых предполагает работу в нелицензируемых полосах частот. § Проблема состоит в том, что требуется обеспечить устойчивую связь с наибольшим числом абонентов на выделенном диапазоне. § Кратко рассмотрим один из методов использования широкополосного диапазона в стандартах Wi-Fi, это § метод ортогонального мультиплексирования OFDM § (Orthogonal Frequency Division Multiplexing).
 2. 2. Необходимые математические понятия § Стандарт 802. 11 a предназначен для диапазона частот около 5 ГГц, он использует технологию OFDM обменивается данными со скоростью 54 Мбит/с. § Стандарт 802. 11 g работает в диапазоне частот 2, 4 ГГц, использует технологию OFDM и также обеспечивает скорость передачи 54 Мбит/с. § Модуляция OFDM позволяет увеличить скорость передачи и информационную емкость канала передачи, разделяя широкий канал, занимаемый одной модулированной несущей, на множество близко расположенных узкополосных каналов, занимаемых несущими, каждая из которых использует свою частоту. Но соседние несущие расположены близко друг к другу, они смешиваются и создают взаимные помехи. Несущие разделяют методом ортогонализации, они образуют ортогональную систему сигналов.
2. 2. Необходимые математические понятия § Стандарт 802. 11 a предназначен для диапазона частот около 5 ГГц, он использует технологию OFDM обменивается данными со скоростью 54 Мбит/с. § Стандарт 802. 11 g работает в диапазоне частот 2, 4 ГГц, использует технологию OFDM и также обеспечивает скорость передачи 54 Мбит/с. § Модуляция OFDM позволяет увеличить скорость передачи и информационную емкость канала передачи, разделяя широкий канал, занимаемый одной модулированной несущей, на множество близко расположенных узкополосных каналов, занимаемых несущими, каждая из которых использует свою частоту. Но соседние несущие расположены близко друг к другу, они смешиваются и создают взаимные помехи. Несущие разделяют методом ортогонализации, они образуют ортогональную систему сигналов.
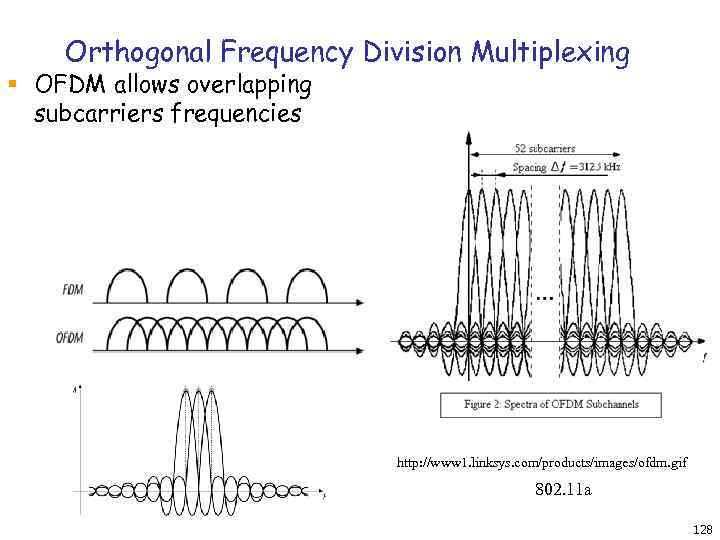 Orthogonal Frequency Division Multiplexing § OFDM allows overlapping subcarriers frequencies http: //www 1. linksys. com/products/images/ofdm. gif 802. 11 a 128
Orthogonal Frequency Division Multiplexing § OFDM allows overlapping subcarriers frequencies http: //www 1. linksys. com/products/images/ofdm. gif 802. 11 a 128
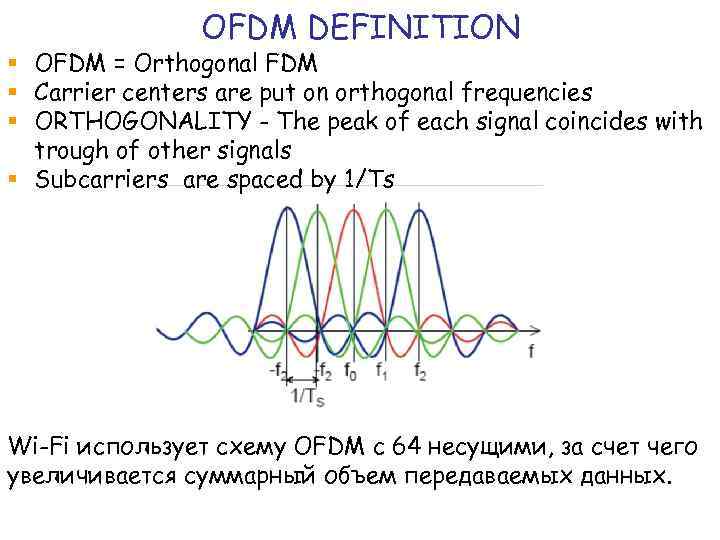 OFDM DEFINITION § OFDM = Orthogonal FDM § Carrier centers are put on orthogonal frequencies § ORTHOGONALITY - The peak of each signal coincides with trough of other signals § Subcarriers are spaced by 1/Ts Wi-Fi использует схему OFDM с 64 несущими, за счет чего увеличивается суммарный объем передаваемых данных.
OFDM DEFINITION § OFDM = Orthogonal FDM § Carrier centers are put on orthogonal frequencies § ORTHOGONALITY - The peak of each signal coincides with trough of other signals § Subcarriers are spaced by 1/Ts Wi-Fi использует схему OFDM с 64 несущими, за счет чего увеличивается суммарный объем передаваемых данных.
 2. 2. Необходимые математические понятия § Сигналы на соседних несущие ортогональны, поэтому из суммарного смешанного сигнала можно выделить сигнал x(t), вычисляя скалярное произведение x(t) с суммарным смешанным сигналом. § Таким образом, примитивном использовании широкой полосы скорость передачи 6 Мбит/c; § метод OFDM увеличивает скорость до 54 Мбит/с. § Пример. Пусть точка доступа передает сигналы трем абонентам методом OFDM использования широкой полосы на трех несущих. § Применим простейшую амплитудную модуляцию с передачей одного из чисел -3, -2, -1, 0, 1, 2, 3 (семь чисел) за квант времени, квант равен 2 единицам времени (секунда, миллисекунда, наносекунда – любая единица, но аппаратура за квант времени должна распознать сигнал). Условно будем считать, что этот передача выполняется за интервал времени [-1, 1].
2. 2. Необходимые математические понятия § Сигналы на соседних несущие ортогональны, поэтому из суммарного смешанного сигнала можно выделить сигнал x(t), вычисляя скалярное произведение x(t) с суммарным смешанным сигналом. § Таким образом, примитивном использовании широкой полосы скорость передачи 6 Мбит/c; § метод OFDM увеличивает скорость до 54 Мбит/с. § Пример. Пусть точка доступа передает сигналы трем абонентам методом OFDM использования широкой полосы на трех несущих. § Применим простейшую амплитудную модуляцию с передачей одного из чисел -3, -2, -1, 0, 1, 2, 3 (семь чисел) за квант времени, квант равен 2 единицам времени (секунда, миллисекунда, наносекунда – любая единица, но аппаратура за квант времени должна распознать сигнал). Условно будем считать, что этот передача выполняется за интервал времени [-1, 1].
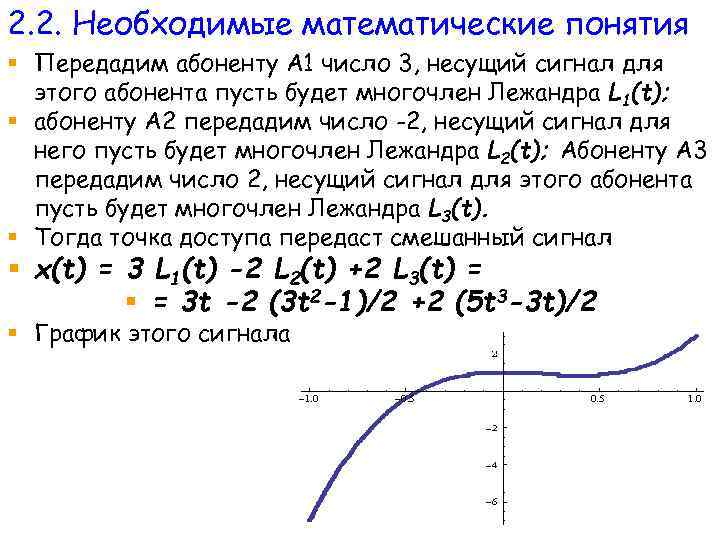 2. 2. Необходимые математические понятия § Передадим абоненту А 1 число 3, несущий сигнал для этого абонента пусть будет многочлен Лежандра L 1(t); § абоненту А 2 передадим число -2, несущий сигнал для него пусть будет многочлен Лежандра L 2(t); Абоненту А 3 передадим число 2, несущий сигнал для этого абонента пусть будет многочлен Лежандра L 3(t). § Тогда точка доступа передаст смешанный сигнал § x(t) = 3 L 1(t) -2 L 2(t) +2 L 3(t) = § = 3 t -2 (3 t 2 -1)/2 +2 (5 t 3 -3 t)/2 § График этого сигнала
2. 2. Необходимые математические понятия § Передадим абоненту А 1 число 3, несущий сигнал для этого абонента пусть будет многочлен Лежандра L 1(t); § абоненту А 2 передадим число -2, несущий сигнал для него пусть будет многочлен Лежандра L 2(t); Абоненту А 3 передадим число 2, несущий сигнал для этого абонента пусть будет многочлен Лежандра L 3(t). § Тогда точка доступа передаст смешанный сигнал § x(t) = 3 L 1(t) -2 L 2(t) +2 L 3(t) = § = 3 t -2 (3 t 2 -1)/2 +2 (5 t 3 -3 t)/2 § График этого сигнала
 2. 2. Необходимые математические понятия § Получив смешанный сигнал x(t), приемное устройство абонента А 1 находит коэффициент разложения этого сигнала при многочлене Лежандра L 1(t); § абонент А 2 находит коэффициент разложения этого сигнала при многочлене Лежандра L 2(t); § абонент А 3 находит коэффициент разложения этого сигнала при многочлене Лежандра L 3(t). § Абоненты получают числа 3, -2, 2.
2. 2. Необходимые математические понятия § Получив смешанный сигнал x(t), приемное устройство абонента А 1 находит коэффициент разложения этого сигнала при многочлене Лежандра L 1(t); § абонент А 2 находит коэффициент разложения этого сигнала при многочлене Лежандра L 2(t); § абонент А 3 находит коэффициент разложения этого сигнала при многочлене Лежандра L 3(t). § Абоненты получают числа 3, -2, 2.
