2. ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ. 2. 1. ЗАКОНЫ НЬЮТОНА.

2. ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ. 2. 1. ЗАКОНЫ НЬЮТОНА. ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ. ЦЕНТР МАСС. УРАВНЕНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС. ПОСТУЛАТЫ КЛАССИЧЕСКОЙ МЕХАНИКИ (законы Ньютона) Первый закон Ньютона (закон инерции) постулирует и содержит определение инерциальной системы отсчета (ИСО) : существуют такие системы отсчета, называемые инерциальными, относительно которых тело (МТ) движется прямолинейно и равномерно либо покоится, если отсутствуют какие бы то ни было воздействия на него со стороны других материальных точек или тел. Таким образом, т. н. свободная МТ либо покоится относительно ИСО, либо движется по инерции, и это движение в ИСО – равномерное и прямолинейное. Из определения ИСО следует, что любая СО, движущаяся относительно некоторой ИСО поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета.

При наличии воздействия на МТ скорость ее изменяется, она приобретает ускорение, которое зависит от инертности МТ, а также от направления и интенсивности воздействия. Мерой инертности материальной точки (тела) является ее масса (m). Воздействие на МТ со стороны другой механической системы (материальной точки, тела и т. д. ) определяется векторной величиной – силой. Второй закон Ньютона гласит: ускорение, приобретаемое материальной точкой массой m под действием силы , сонаправлено с силой, а величина его прямо пропорциональна величине силы и обратно пропорциональна массе материальной точки: , (2. 1 а) где b=const – положительная постоянная, зависящая от выбора системы единиц.

В системе СИ b=1 и второй закон можно записать в форме уравнения движения для МТ (тела): (2. 1 б) Если на МТ действуют не одна сила, а n сил, то каждая i-тая сила сообщает МТ ускорение независимо от других сил, а результирующее ускорение МТ будет равно векторной сумме ускорений, сообщаемых каждой силой в отдельности: (2. 1 в) Умножая обе части этого выражения на массу МТ m получим: (2. 1 г) Для каждой силы , действующей на МТ, можно записать выражение второго закона Ньютона: (2. 1 д) Подставив (2. 1 д) в (2. 1 г), получим: обозначим через , т. е. : (2. 1 е) (2. 1 ж) Последнее выражение называют принципом суперпозиции сил. Здесь сила называется равнодействующей всех сил, приложенных к МТ.

Третий закон Ньютона описывает взаимодействие двух тел (МТ). Если одно тело действует на другое с некоторой силой, то и другое тело действует на первое с силой, равной по величине и направленной противоположно: (2. 2) где – сила, действующая на тело 1 со стороны тела 2, а – сила, действующая на тело 2 со стороны тела 1.

Основная задача динамики для механической системы в простейшей постановке формулируется так: Известны все силы , действующие на все материальные точки системы, известны начальные положения и начальные скорости всех материальных точек системы. Найти закон движения системы, а также закон движения для каждой материальной точки, входящей в состав системы. Пример. Пусть система состоит из одной материальной точки массы . Известна – сумма сил, действующих на нее. Заданы начальные значения радиуса-вектора и скорости м. т. и . Найдем закон движения материальной точки. Ускорение определяем с помощью уравнения движения (второго закона Ньютона) (2. 3) а дальше пользуемся соотношениями кинематики (см. Лекцию № 1, равенства (1. 15), (1. 16)), интегрируем (2. 3) два раза по времени:

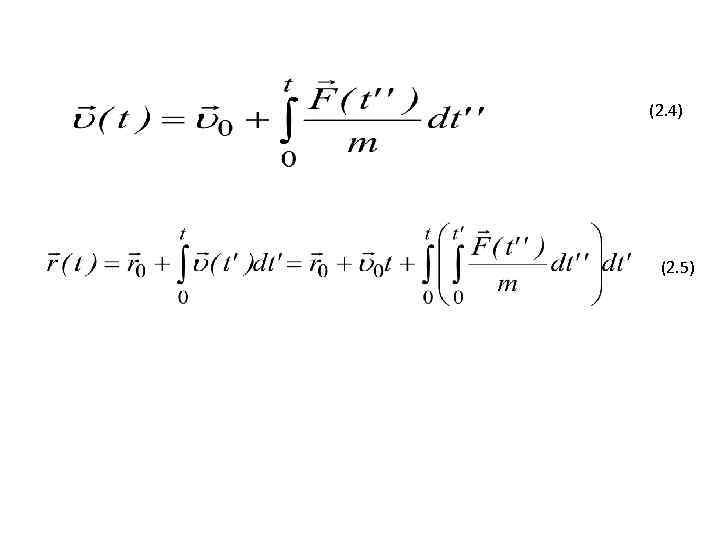(2. 4) (2. 5)

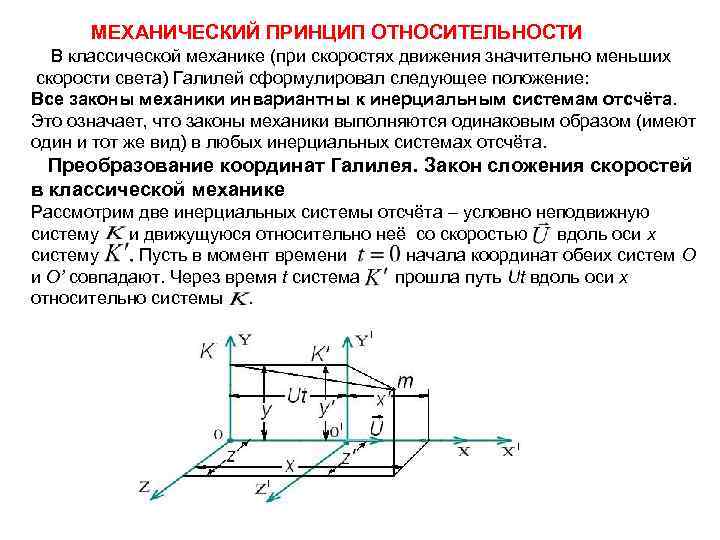МЕХАНИЧЕСКИЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В классической механике (при скоростях движения значительно меньших скорости света) Галилей сформулировал следующее положение: Все законы механики инвариантны к инерциальным системам отсчёта. Это означает, что законы механики выполняются одинаковым образом (имеют один и тот же вид) в любых инерциальных системах отсчёта. Преобразование координат Галилея. Закон сложения скоростей в классической механике Рассмотрим две инерциальных системы отсчёта – условно неподвижную систему и движущуюся относительно неё со скоростью вдоль оси x систему Пусть в момент времени начала координат обеих систем О и O’ совпадают. Через время t система прошла путь Ut вдоль оси x относительно системы .

Из рисунка видно, что связь координат материальной точки m в системе К x. y, z с её координатами x’, y’, z’ в системе К’ следующая: Последняя формула означает, что время в различных инерциальных системах отсчёта течёт одинаково. Приведенные выше выражения носят название преобразований Галилея. Продифференцируем первые три выражения по времени: или Последние три формулы справа называют законом сложения скоростей Галалея в координатной форме. Здесь , , ─ компоненты скорости материальной точки относительно системы К, а , , ─ компоненты скорости той же материальной точки относительно системы К’.

Нетрудно понять, что в векторной форме закон сложения скоростей будет иметь вид: . Взяв производную по времени от последнего выражения, получим: или Отсюда следует, что ускорение материальной точки не изменяется при переходе из одной инерциальной системы отсчёта к другой. Величины, обладающие этим свойством, называются инвариантами. Так как причиной ускорения является сила, то она также является инвариантом: Применив второй закон Ньютона, нетрудно понять, что инвариантом также является масса: Итак, из рассмотренных нами величин: инварианты ─ время, ускорение, сила, масса; неинварианты ─ координаты, скорость, радиус-вектор, перемещение. Необходимо подчеркнуть, что всё сказанное в этом разделе относится только к классической механике (v<

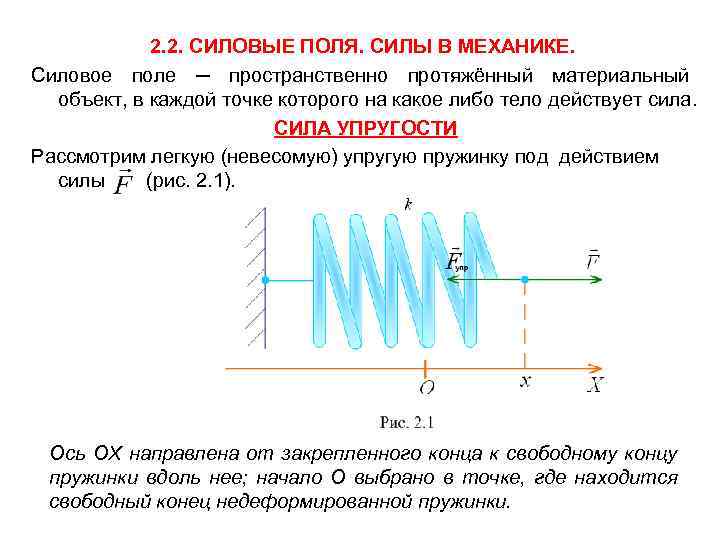2. 2. СИЛОВЫЕ ПОЛЯ. СИЛЫ В МЕХАНИКЕ. Силовое поле ─ пространственно протяжённый материальный объект, в каждой точке которого на какое либо тело действует сила. СИЛА УПРУГОСТИ Рассмотрим легкую (невесомую) упругую пружинку под действием силы (рис. 2. 1). Ось OX направлена от закрепленного конца к свободному концу пружинки вдоль нее; начало О выбрано в точке, где находится свободный конец недеформированной пружинки.

Результатом действия деформирующей силы является возникновение силы упругости , равной по величине силе и противоположно ей направленной, а также удлинения пружинки, которое равно (2. 6) – длина недеформированной пружинки. Очевидно (2. 7) – отклонение свободного конца от положения равновесия. Величина удлинения упругой пружинки прямо пропорциональна величине деформирующей силы F, а, следовательно, силе упругости : (2. 8) А т. к. , то в проекциях на ось OX : (2. 8 a) где – положительная постоянная, называемая коэффициентом упругости или коэффициентом жесткости пружинки. Уравнения (2. 8) и (2. 8 а) – закон Гука, описывающий упругую деформацию тела. PS. Деформация – это изменение формы и (или) размеров тела. Деформация называется упругой, если деформированное тело после снятия нагрузки восстанавливает свою форму и размеры. В противном случае деформация называется пластической. Таким образом, упругая – это обратимая деформация, а пластическая – необратимая.

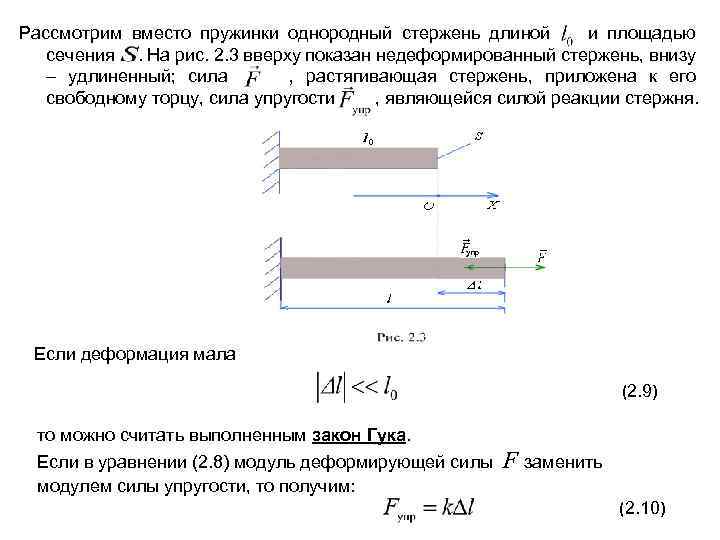Рассмотрим вместо пружинки однородный стержень длиной и площадью сечения . На рис. 2. 3 вверху показан недеформированный стержень, внизу – удлиненный; сила , растягивающая стержень, приложена к его свободному торцу, сила упругости , являющейся силой реакции стержня. Если деформация мала (2. 9) то можно считать выполненным закон Гука. Если в уравнении (2. 8) модуль деформирующей силы F заменить модулем силы упругости, то получим: (2. 10)

Здесь – коэффициент упругости (жесткости) стержня, зависящий, очевидно, от материала образца, площади сечения и длины стержня . Относительная деформация (относительное удлинение): (2. 11) Напряжение: (2. 12) Используя (2. 8) и (2. 11), перепишем (2. 12) в виде (2. 13) Обозначив , (2. 13 а) приводим закон Гука к следующему виду: , (2. 14) здесь – модуль Юнга. Посмотрев на формулу (2. 13 а) можно прийти к заблуждению, что Е есть функция площади сечения S и длины стержня l 0. На самом же деле это k есть функция от площади сечения и длины, а модуль Юнга определяется только материалом стержня и не зависит ни от S ни от lo.

Форма (2. 14) записи закона Гука имеет следующие преимущества. 1. Модуль Юнга определяется только материалом образца и не зависит от его размеров (как коэффициент упругости ); 2. – табличная величина. Например, для стали =2, 1∙ 1011 Па; 1 Па=1 Н/м 2. 3. Коэффициент упругости стержня с известными значениями сечения , длины и материала ( ), можно вычислить, используя формулу (2. 13 а): (2. 15)

СИЛА ТРЕНИЯ Трение, которое мы рассмотрим очень коротко, подразделяется на сухое и вязкое (жидкое). Применительно к сухому трению различают трение скольжения, трение покоя и трение качения (подробно не будем рассматривать). При скольжении одного тела по поверхности другого на каждый элемент поверхности первого тела, находящийся в контакте со вторым телом, действуют силы. Это – силы реакции элементов поверхности второго тела. Оказывается, что сила трения скольжения не зависит от площади соприкосновения трущихся тел и пропорциональна величине силы нормального давления (нормальной реакции поверхностей), прижимающей трущиеся поверхности друг к другу: (2. 16) Безразмерный коэффициент называется коэффициентом трения. Он зависит от природы и состояния трущихся поверхностей и, в частности от их шероховатости. Коэффициент трения может зависеть также от относительной скорости тел, которой пренебрегают при небольших скоростях.

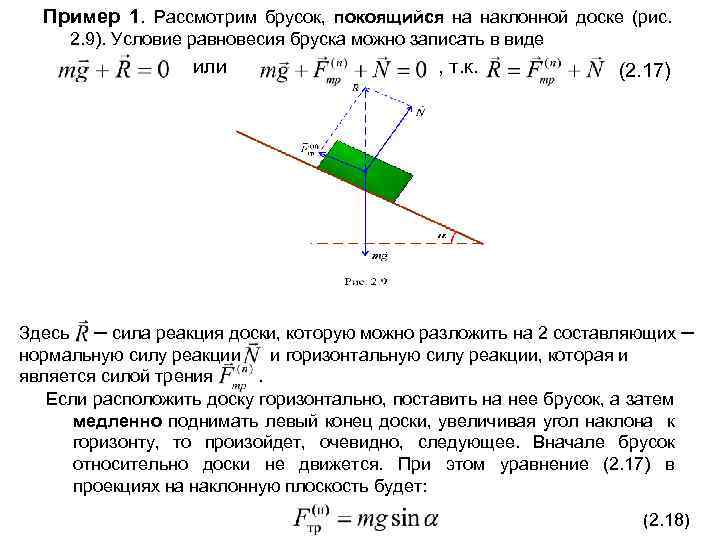Пример 1. Рассмотрим брусок, покоящийся на наклонной доске (рис. 2. 9). Условие равновесия бруска можно записать в виде или , т. к. (2. 17) Здесь ─ сила реакция доски, которую можно разложить на 2 составляющих ─ нормальную силу реакции и горизонтальную силу реакции, которая и является силой трения . Если расположить доску горизонтально, поставить на нее брусок, а затем медленно поднимать левый конец доски, увеличивая угол наклона к горизонту, то произойдет, очевидно, следующее. Вначале брусок относительно доски не движется. При этом уравнение (2. 17) в проекциях на наклонную плоскость будет: (2. 18)

– и так – вплоть до некоторого угла , при котором начинается медленное соскальзывание. При медленном соскальзывании можно считать ускорение бруска пренебрежимо малым, и тогда силу трения, являющуюся силой трения скольжения, можно вычислить по формуле, аналогичной (2. 18): (2. 19) Выражения (2. 18) и (2. 19) позволяют сделать вывод, что сила трения покоя, возникающая при попытке сдвинуть тело относительно поверхности другого тела, с которым оно находится в контакте, подчинена неравенству (2. 20) Таким образом, ограничение сверху на силу трения покоя имеет вид (см. (2. 16)): (2. 21)

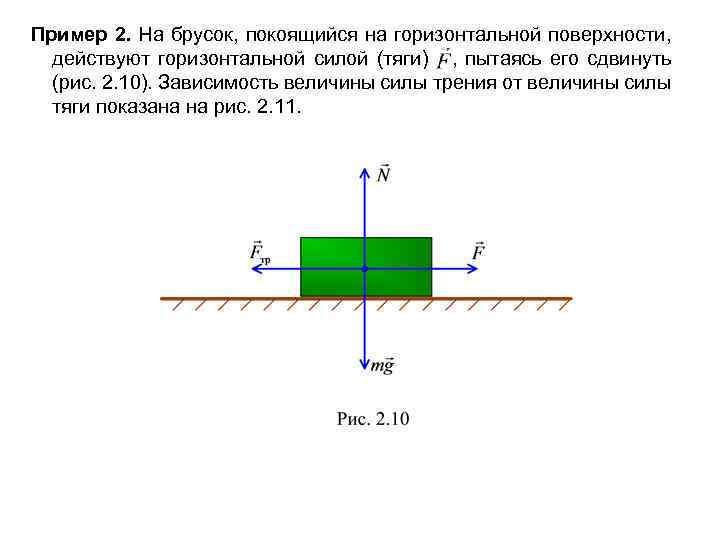Пример 2. На брусок, покоящийся на горизонтальной поверхности, действуют горизонтальной силой (тяги) , пытаясь его сдвинуть (рис. 2. 10). Зависимость величины силы трения от величины силы тяги показана на рис. 2. 11.

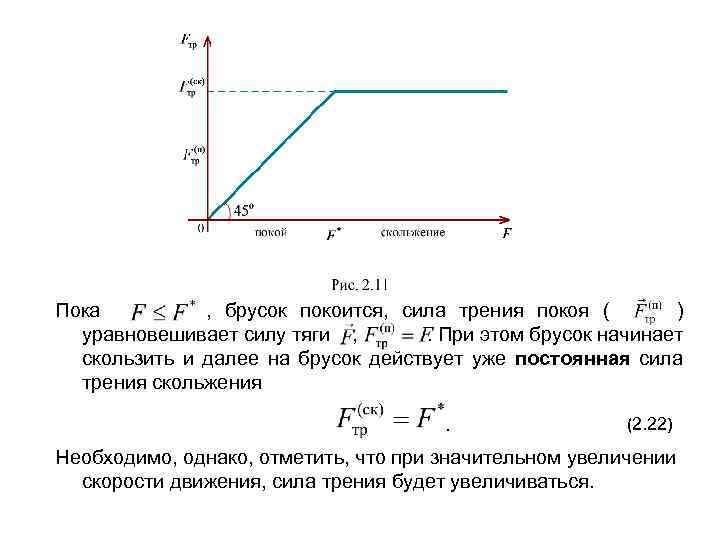Пока , брусок покоится, сила трения покоя ( ) уравновешивает силу тяги , . При этом брусок начинает скользить и далее на брусок действует уже постоянная сила трения скольжения . (2. 22) Необходимо, однако, отметить, что при значительном увеличении скорости движения, сила трения будет увеличиваться.

Вязкое трение. При движении твердого тела относительно жидкости или газа на тело действуют силы сопротивления среды - силы вязкого трения. Следует отметить, что вязкого трения покоя не существует; сила сопротивления действует только на движущееся относительно среды тело, т. е. при . При малых скоростях тела (когда обтекание тела средой можно считать ламинарным), сила сопротивления пропорциональна скорости тела: (2. 23) r – положительный коэффициент сопротивления, зависящий от формы и размеров тела, ориентации тела относительно вектора скорости , состояния его поверхности и свойства среды, называемого вязкостью.

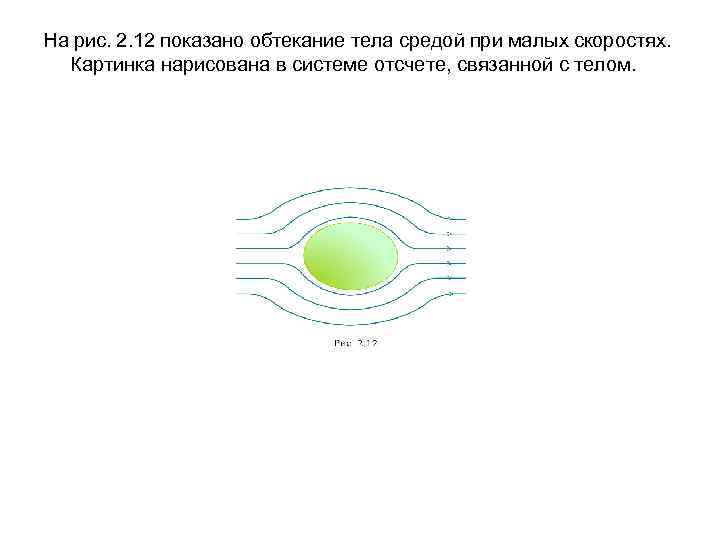На рис. 2. 12 показано обтекание тела средой при малых скоростях. Картинка нарисована в системе отсчете, связанной с телом.

2. 3. Движение заряженной частицы в постоянных электрическом и магнитном полях. На точечный электрический заряд в электромагнитном поле действует сила: (2. 24) где ─ напряженность электрического поля, - индукция магнитного поля. Первое слагаемое – сила, действующая со стороны электрического поля; второе – сила, действующая со стороны поля магнитного. Магнитная сила: называется магнитной силой Лоренца. PS. 1) Магнитное поле на покоящийся заряд не действует: при сила Лоренца обращается в ноль. 2) Сила Лоренца перпендикулярна как скорости частицы , так и индукции магнитного поля : (2. 25)

. , , . Рассмотрим уравнение движения частицы с зарядом и массой в электрическом поле . Тогда (2. 26) В случае получаем . (2. 27) Тогда, проинтегрировав (2. 27)(см. Лекцию № 1), можно записать: (2. 28) Проинтегрировав (2. 28), получаем: (2. 29) где – начальная скорость, – начальное значение радиус-вектора частицы. Закон движения частицы (2. 29) содержит полную информацию о ее движении: траектория частицы – либо прямая, параллельная силовым линиям поля при , либо парабола, ось которой параллельна линиям поля при . (почему – подумать!).

Рассмотрим уравнение движения частицы в магнитном поле . (2. 30) Прежде всего разложим скорость частицы на две составляющие: , (2. 31) – так, как показано на рис. 2. 13; – составляющая скорости, параллельная силовым линиям магнитного поля, направлена по или противоположно (в зависимости от угла между и ); – составляющая, перпендикулярная силовым линиям. Очевидно, . . (2. 32 а, б) Подставляя разложение (2. 31) в уравнение (2. 30), получаем . (2. 33)

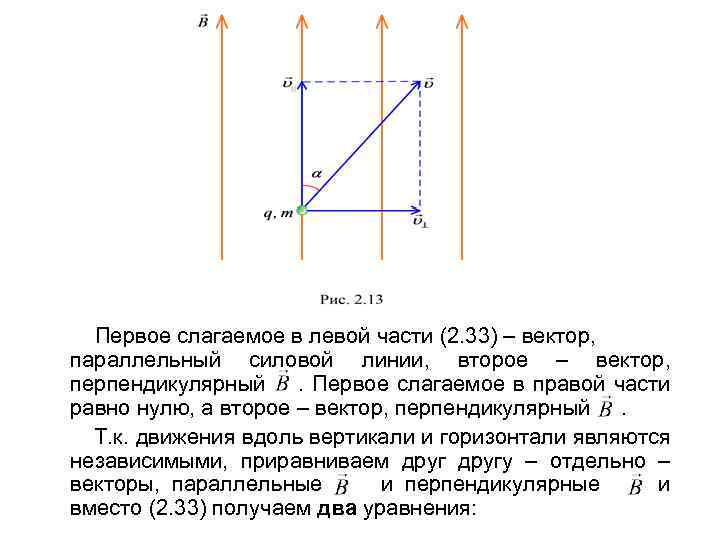Первое слагаемое в левой части (2. 33) – вектор, параллельный силовой линии, второе – вектор, перпендикулярный . Первое слагаемое в правой части равно нулю, а второе – вектор, перпендикулярный . Т. к. движения вдоль вертикали и горизонтали являются независимыми, приравниваем другу – отдельно – векторы, параллельные и перпендикулярные и вместо (2. 33) получаем два уравнения:

, (2. 34 а) . (2. 34 б) Из (2. 34 а) следует . (2. 35) Если , получаем самый простой вариант движения частицы – равномерное движение вдоль прямолинейной силовой линии. Пусть теперь , =0 . Интегрируя уравнение поперечного движения (2. 34 б), получаем . (2. 36) Отсюда следует . (2. 37)

Введем обозначение . (2. 38) Тогда (2. 37) приобретает вид: . (2. 39) Это соотношение показывает (см. лекцию №I), что поперечное движение частицы представляет собой равномерное движение по окружности радиуса c угловой скоростью , определяемой равенством (2. 38). Величина (2. 40) называется также циклотронной частотой вращения частицы. PS. Эта величина не зависит ни от модуля скорости частицы, ни от угла между и .

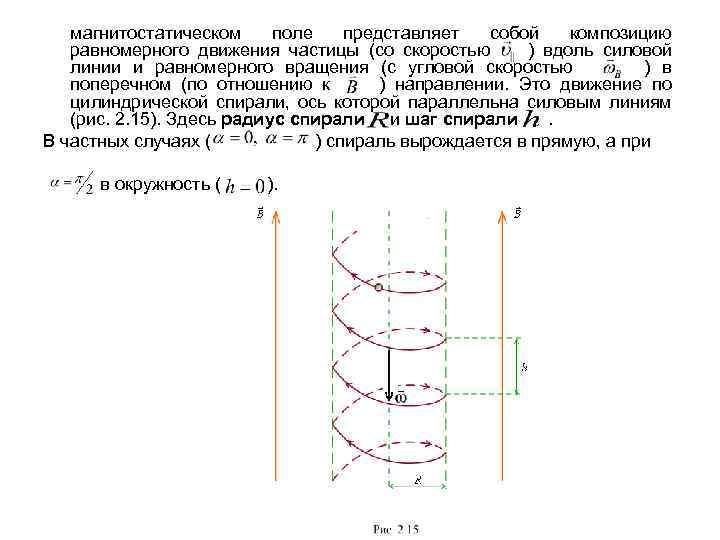магнитостатическом поле представляет собой композицию равномерного движения частицы (со скоростью ) вдоль силовой линии и равномерного вращения (с угловой скоростью ) в поперечном (по отношению к ) направлении. Это движение по цилиндрической спирали, ось которой параллельна силовым линиям (рис. 2. 15). Здесь радиус спирали и шаг спирали . В частных случаях ( ) спираль вырождается в прямую, а при в окружность ( ).

2. 4. Закон всемирного тяготения. Принцип суперпозиции для ньютоновых гравитационных сил. Гравитационное поле. Напряженность гравитационного поля. Первая космическая скорость. Вес тела. В ньютоновой механике ( ) гравитационное взаимодействие определяется законом всемирного тяготения, открытым Ньютоном: Любые две материальные точки взаимодействуют между собой силами гравитационного притяжения; эти силы направлены вдоль отрезка, соединяющего материальные точки, величина этих сил пропорциональна массам материальных точек и обратно пропорциональна квадрату расстояния между ними: . (2. 41)

В выражении для силы гравитационного взаимодействия (2. 41) , - так называемые гравитационные массы, которые, как выяснилось, совпадают с известными нам инертными массами материальных точек. Коэффициент пропорциональности называется гравитационной постоянной: Н. м 2/кг 2 В векторной форме: , (2. 42) см. рис. 2. 17.

Гравитационные силы подчиняются принципу суперпозиции. (2. 43) где – сила, действующая на со стороны .

Напряжённость гравитационного поля. Отношение силы к массе материальной точки не зависит от массы и, поэтому, является силовой характеристикой гравитационного поля. Эта величина (2. 44) называется напряженностью гравитационного поля (поля силы тяжести). Ясно, что , время здесь рассматривается как параметр. Очевидно, принцип суперпозиции можно сформулировать и на языке напряженностей; вместо (2. 43) будем иметь: (2. 45)

Введем определение. Свободным падением материальной точки (тела) называется ее движение под действием одной лишь силы тяжести (гравитационной силы). Из второго закона Ньютона тогда следует, что напряженность гравитационного поля совпадает с ускорением свободного падения частицы. Пример 1. Рассмотрим планету радиуса и массы и будем считать распределение массы по ее объему центральносимметричным. Тогда на МТ , находящуюся на расстоянии от центра планеты на высоте над ее поверхностью, действует сила тяжести . (2. 46) Ускорение свободного падения на высоте h: (2. 47)

У поверхности планеты ( ) . (2. 48) Из (2. 47) и (2. 48) следует . (2. 49) Пример 2. Пусть имеется спутник , движущийся вокруг планеты по круговой орбите на высоте h (рис. 2. 20). Центростремительное ускорение спутника совпадает с ускорением свободного падения: (2. 50) Отсюда скорость спутника (2. 51)

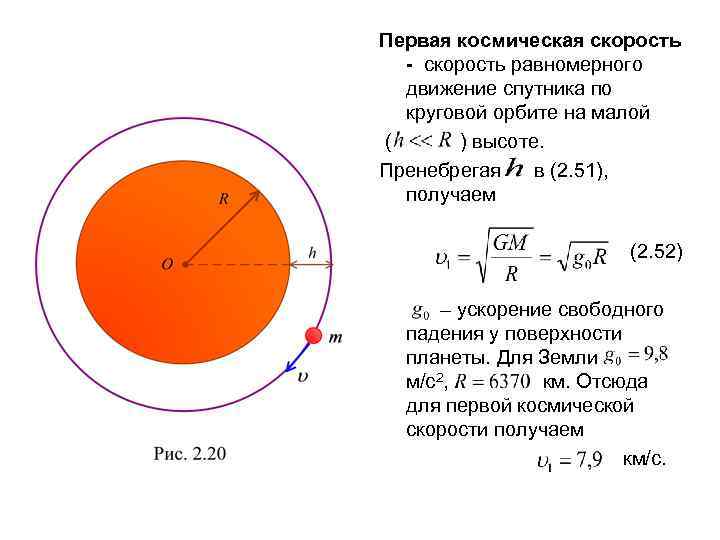Первая космическая скорость - скорость равномерного движение спутника по круговой орбите на малой ( ) высоте. Пренебрегая в (2. 51), получаем (2. 52) – ускорение свободного падения у поверхности планеты. Для Земли м/с2, км. Отсюда для первой космической скорости получаем км/с.

Весом тела называется сила, с которой тело, находящееся в поле сил тяжести , действует на опору или подвес, препятствующие свободному падению тела. На рис. 2. 21 показаны силы, действующие на тело , которое покоится относительно поверхности Земли на широте : – сила гравитации (тяготения), направленная к центру Земли О, – сила реакции поверхности. Рассмотрим зависимость веса тела от географической широты местности . Тело участвует в суточном вращении Земли и, следовательно, движется по окружности радиуса , (2. 53) совпадающей с параллелью. По второму закону Ньютона, , (2. 54)

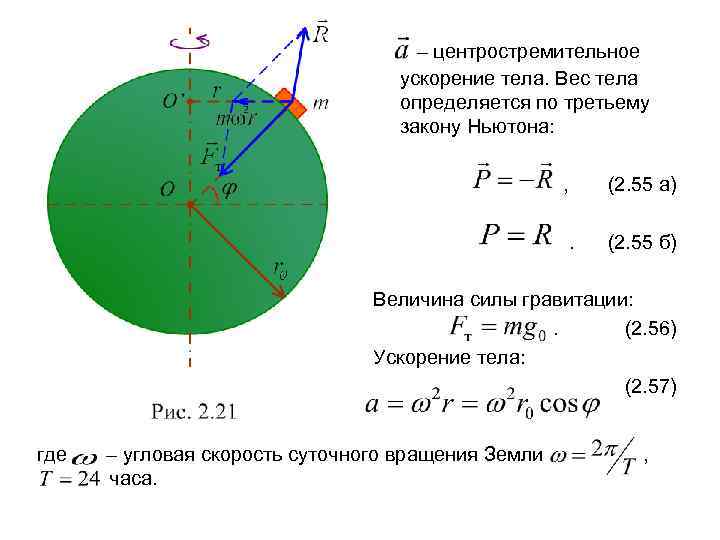– центростремительное ускорение тела. Вес тела определяется по третьему закону Ньютона: , (2. 55 а) . (2. 55 б) Величина силы гравитации: . (2. 56) Ускорение тела: (2. 57) где – угловая скорость суточного вращения Земли , часа.

Величина веса определяется с помощью теоремы косинусов: (2. 58) Следует заметить, что сила тяжести , действующая на тело со стороны вращающейся Земли, направлена не строго перпендикулярно поверхности Земли, т. к. она равна по модулю и направлена противоположно силе реакции , которая, как видно из рис. 2. 21, также не перпендикулярна поверхности Земли из-за её суточного вращения. Её не следует путать с силой гравитации , где ─ ускорение свободного падения, которое создавала бы сила гравитации в отсутствии суточного вращения Земли. Поэтому реальное ускорение свободного падения только на полюсах Земли, при других же широтах оно несколько меньше, чем . 2. 5. Импульс материальной точки. Импульс механической системы и скорость ее центра масс. Второй закон Ньютона на языке импульса. Закон сохранения импульса. Столкновения. Импульсом материальной точки называется величина (2. 59) где – масса м. т. , – ее скорость (мгновенная). Импульсом механической системы (набор материальных точек) называется величина . (2. 60)

Продифференцируем по времени формулу импульса (2. 60): . (2. 61) Таким образом, второй закон Ньютона в импульсной форме имеет вид: , (2. 62) где – сумма сил, действующих на материальную точку. Перепишем уравнение движения материальной точки в форме . (2. 63) Величина называется импульсом силы за промежуток времени .

Закон сохранения импульса. Рассмотрим следствие уравнения движения (2. 62): Если , то (2. 64) т. е. если сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется. Если на систему тел вообще не действуют внешние силы, то система называется замкнутой. Т. к. условие не противоречит понятию замкнутой системы, то закон сохранения импульса чаще формулируют так: импульс замкнутой системы сохраняется. При этом возможны взаимодействия между телами внутри системы.

Рассмотрим упругое столкновение двух тел. Если система рассматривается как замкнутая, то импульс ее сохраняется и тогда , (2. 65) где – импульсы тел до столкновения, а – после столкновения. Равенство (2. 65) можно переписать в виде (2. 66) где – скорости тел до и после столкновения. Абсолютно неупругим ударом называется такое столкновение (удар), после которого столкнувшиеся тела (частицы) движутся как одно целое, их относительная скорость равна нулю. Закон сохранения импульса для абсолютно неупругого удара можно записать в виде , (2. 67) где – скорость составного тела.

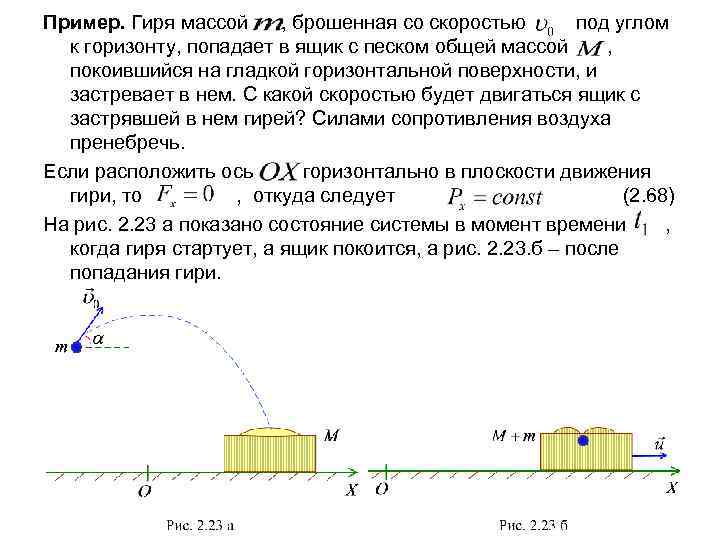Пример. Гиря массой , брошенная со скоростью под углом к горизонту, попадает в ящик с песком общей массой , покоившийся на гладкой горизонтальной поверхности, и застревает в нем. С какой скоростью будет двигаться ящик с застрявшей в нем гирей? Силами сопротивления воздуха пренебречь. Если расположить ось горизонтально в плоскости движения гири, то , откуда следует (2. 68) На рис. 2. 23 а показано состояние системы в момент времени , когда гиря стартует, а ящик покоится, а рис. 2. 23. б – после попадания гири.

Тогда закон сохранения импульса в проекциях на ось OX. (2. 69) Отсюда получаем . (2. 70).

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ НЕЗАМКНУТОЙ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК. ПОНЯТИЕ ЦЕНТРА МАСС Поскольку тело можно рассматривать как систему большого количества материальных точек, все понятия, вводимые нами для системы материальных точек будут относиться и к телу. Поступательным движением системы материальных точек или тела называют такое движение, при котором любая прямая, проведенная через любые две точки системы или тела будет оставаться параллельной самой себе. Рассмотрим поступательное движение системы материальных точек с массами Система называется незамкнутой, если на неё действуют внешние силы и их действие не уравновешивается. Тогда , где ─ равнодействующая всех внешних сил, приложенных к системе. Суммарный импульс всех материальных точек, составляющий систему

Рассмотрим точку, которую в дальнейшем будем называть центром инерции системы, радиус-вектор которой равен: (2. 71) где ─ М суммарная масса всех материальных точек системы, т. е. : (2. 72) Из формулы (2. 71) следует: (2. 73) Подставив (2. 73) в формулу импульса системы, получим: , где ─ не что иное, как скорость центра инерции. Тогда Взяв производную по времени, получим: (2. 73) где ─ не что иное, как ускорение центра инерции. С учётом этого Формулу (2. 73) можно представить в виде: . (2. 74)

Мы получили выражение второго закона Ньютона для материальной точки, расположенной в центре инерции, имеющей массу M, равную сумме масс всех материальных точек нашей незамкнутой системы. Отсюда следует определение центра инерции системы материальных точек или тела: Центром инерции системы материальных точек называется точка, движущаяся как материальная точка, в которой сосредоточена вся масса системы и на которую действует сила, равная равнодействующей всех внешних сил, приложенных к системе.