2. 8 Электро-диффузионные явления 2. 8. 1

2. 8 Электро-диффузионные явления

2. 8. 1 Диффузионный потенциал MНезаряженная мембрана

dxd. C RT dxd. C z. FDj ccc d -плотность тока диффузии катионов dxd. C RTj aa d -плотность тока диффузии анионов dxd. U Cz. F dxd. U j ccc пр -плотность тока проводимости катионов dxd. U Cz. Fj aa пр -плотность тока проводимости анионов a прс прa dc d jjjj — условие равновесия dxd. U Cz. F dxd. C RT acac )()( dxd. U dx Cd z. FRT ac ac ln ac c c CC C n ac a an Числа переноса 1 2 12 ln CC nn z. FRT UU ac

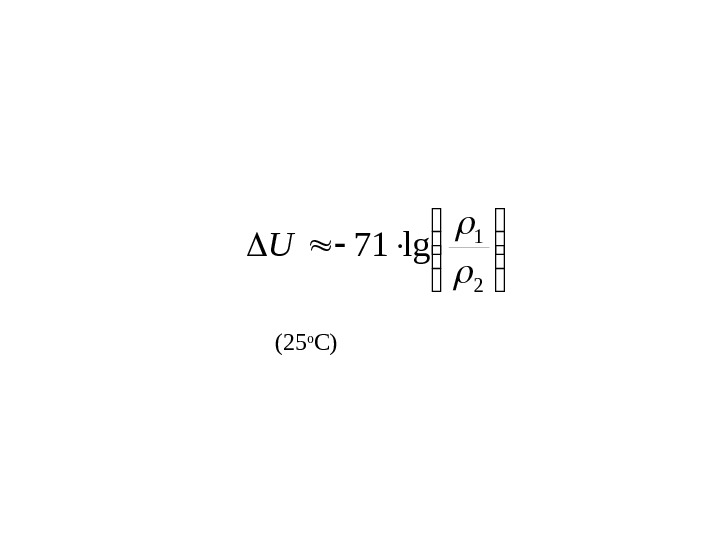
21 lg 71 U (25 o C)

2. 8. 2 Мембранный потенциал Заряженная мембрана M

1 2 12 ln C C nn z. F RT UU acaacc cc c CC C n Числа переноса aacc aa a CC C n Для заряженной мембраны в первом приближении справедлива полученная формула, в которой необходимо учесть новое выражение для чисел переноса :

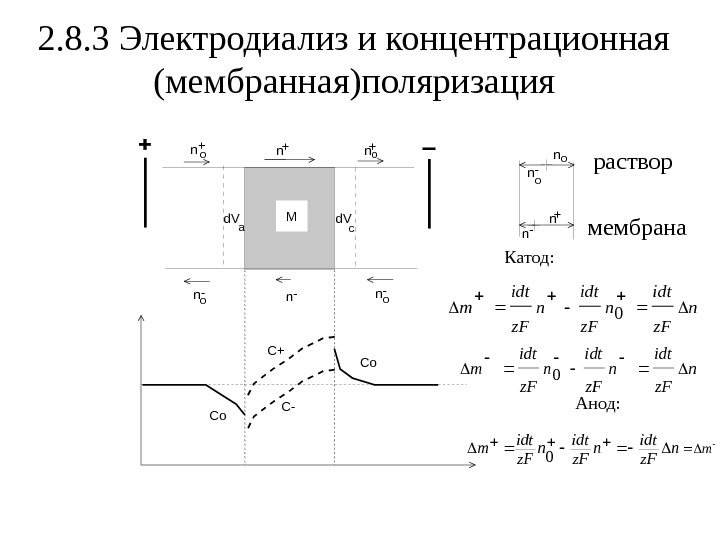
2. 8. 3 Электродиализ и концентрационная ( мембранная ) поляризация Mn n n n+ + + — — -o o n — o n + — n Co Co C+ C-d. V a c раствор мембрана Катод : n z. Fidt m 0 n z. F idt m 0 mn z. Fidt m 0 Анод :

2. 9 Вызванная поляризация

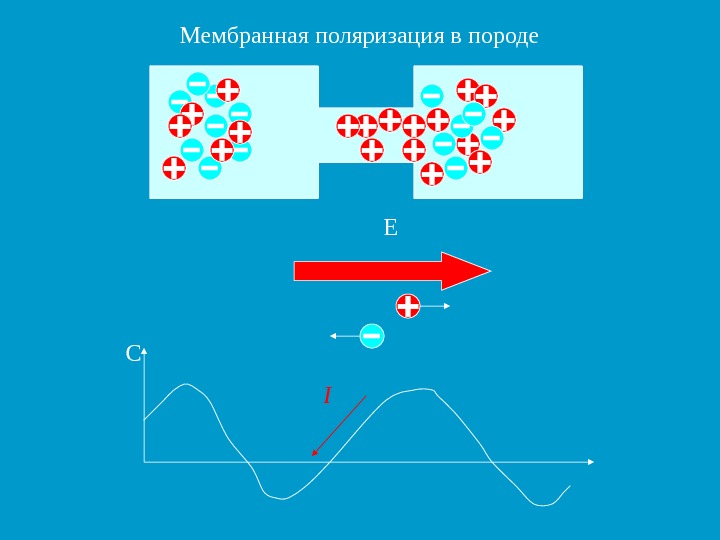
E C Мембранная поляризация в породе I

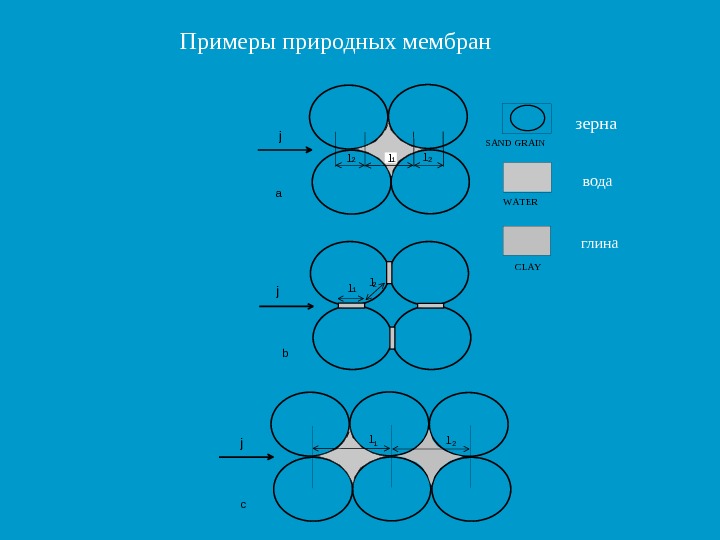
j l 1 l 2 j l l 1 2 a b c SAND GRAIN WATER CLAY Примеры природных мембран зерна вода глина

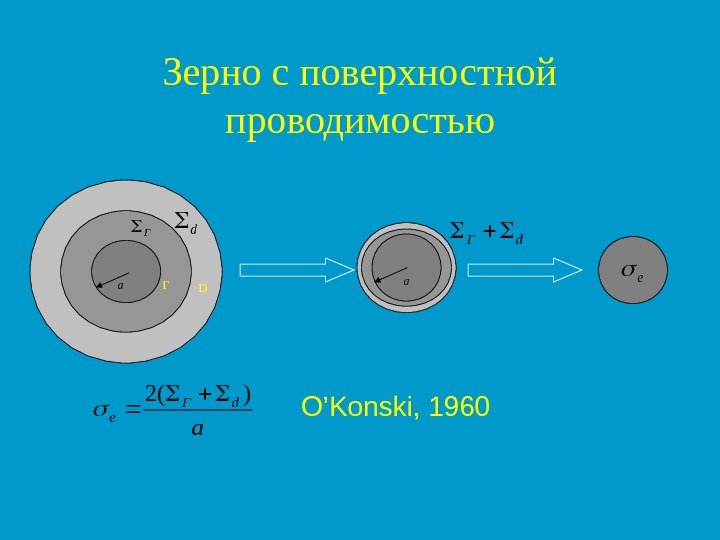
Зерно с поверхностной проводимостью Гd. Г a D d. Г a e a d. Г e )(2 О ’Konski,

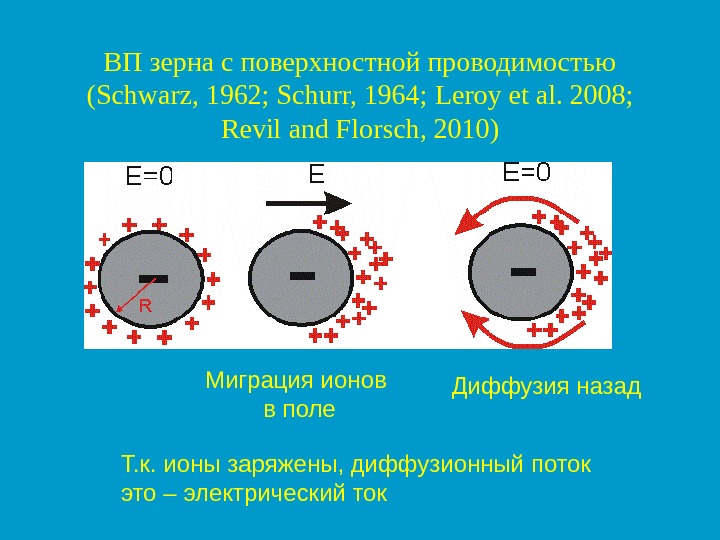
ВП зерна с поверхностной проводимостью ( Schwarz, 1962; Schurr, 1964; Leroy et al. 2008; Revil and Florsch, 2010) Миграция ионов в поле Диффузия назад Т. к. ионы заряжены, диффузионный поток это – электрический ток

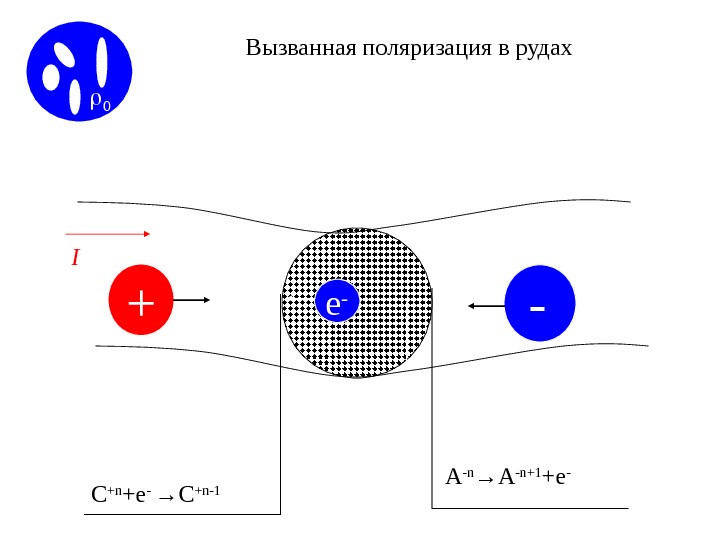
Вызванная поляризация в рудах + -e — A -n →A -n+1 +e — C +n +e — →C +n-1 1 I Вызванная поляризация в рудах

I U I Поляризуемость : t 0 t i+1 U(t) U U и. Временная область (t)=U п /U и Заряжаемость : 2 1 )(1 12 t t dtt ttm

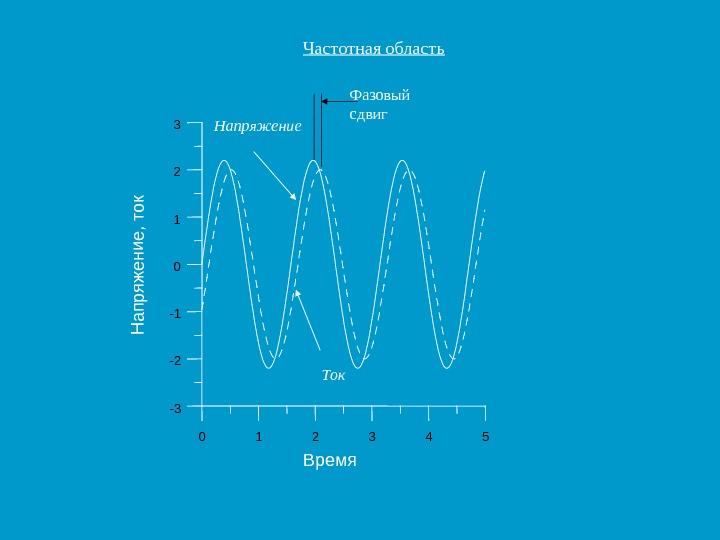
Частотная область 0 1 2 3 4 5 -3 -2 -1 0123 Фазовый сдвиг Ток. Напряжение Время. Н апряж ение, ток

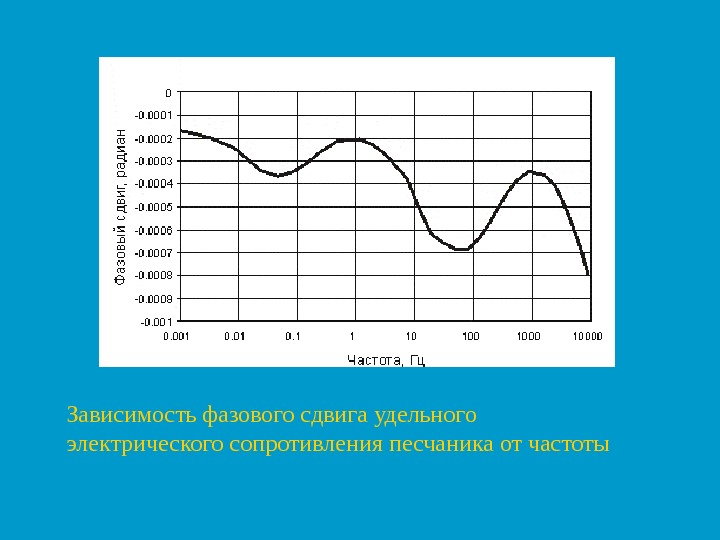
Зависимость фазового сдвига удельного электрического сопротивления песчаника от частоты

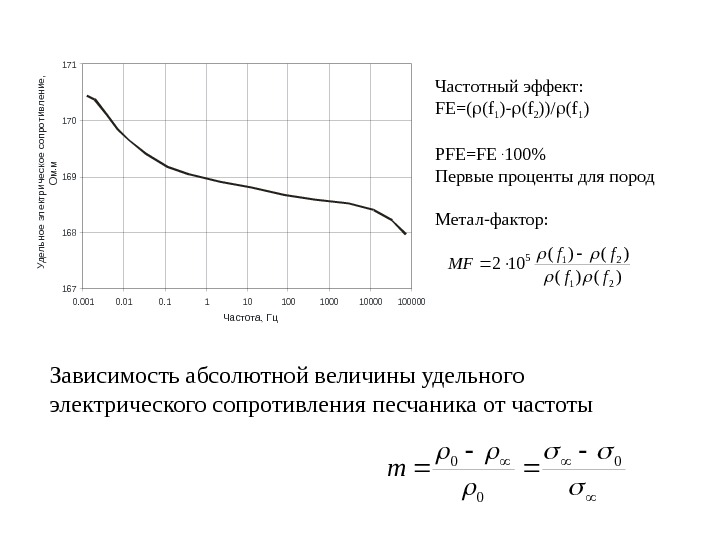
167 168 169 170 171 0. 0010. 111010010000100000 Частота, Гц Удельное электрическое сопротивление, Ом. м Зависимость абсолютной величины удельного электрического сопротивления песчаника от частоты 0 00 m Частотный эффект: FE=( ( f 1 )- (f 2 ))/ (f 1 ) PFE=FE . 100% Первые проценты для пород Метал-фактор : )()( 102 21 215 ff ff M

Эмпирическое описание ВП Формула братьев Коул ( Cole-Cole, 1941) 1 0* )(1 i CC c. CC i)(1 0* c. P i)(1 0* Формула Пелтона ( Pelton et al. , 1978)

• Остаточное напряжение после выключения тока – параметр — поляризуемость • Зависимость удельного сопротивления от времени после включения тока или от частоты тока – параметры : зависимость удельного сопротивления от частоты, частотный эффект • Сдвиг фаз между напряжением и током в частотной области. Проявление и параметры ВП