111 1 12 2 1 1 21 1


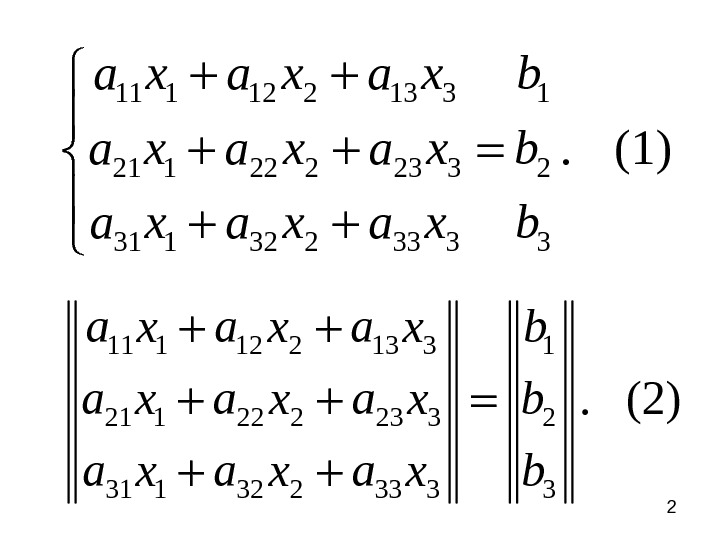
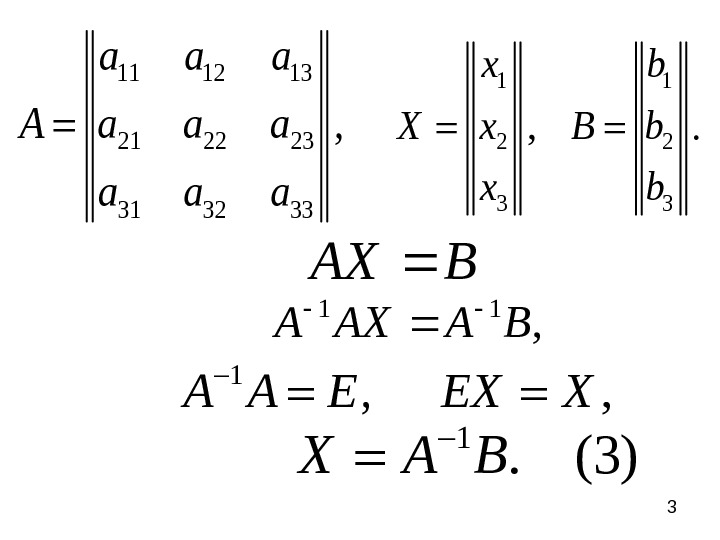

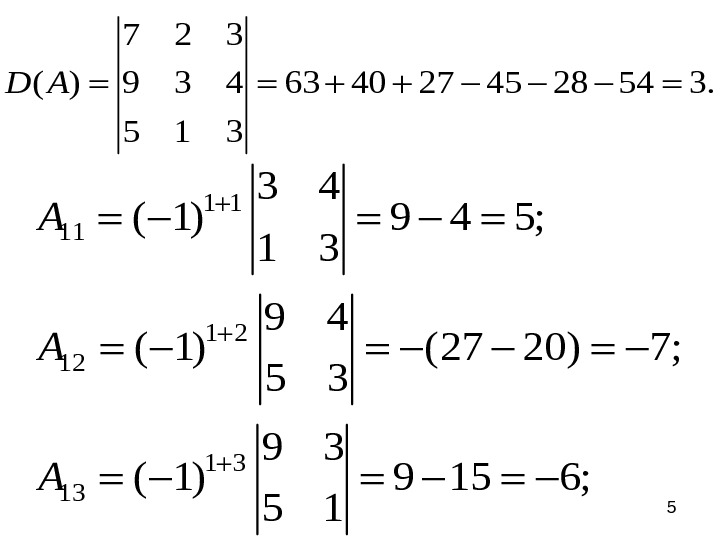
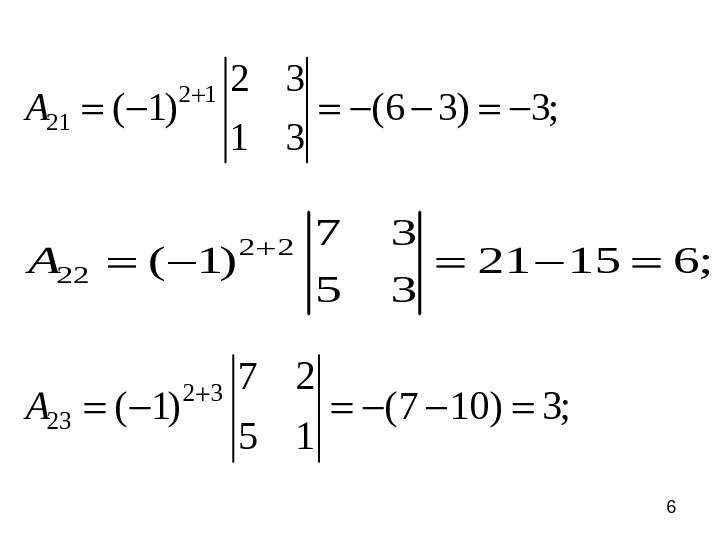
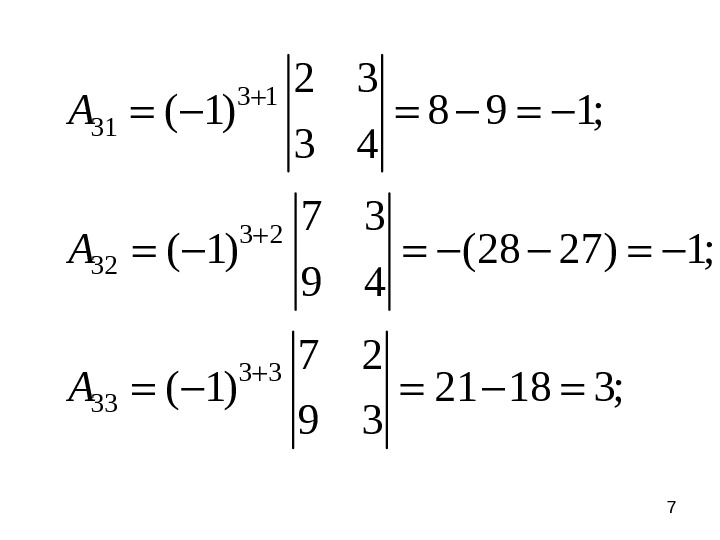





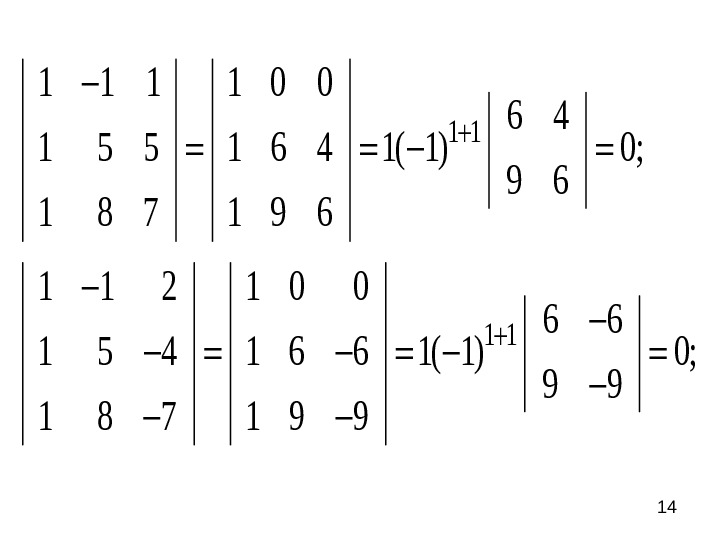
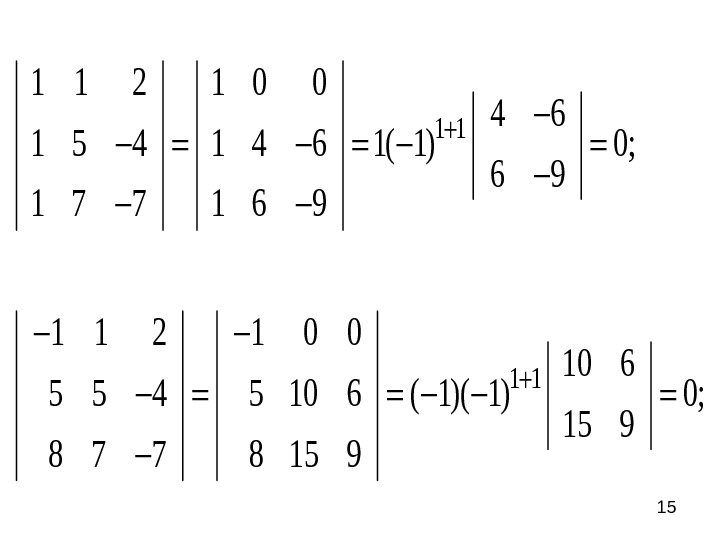


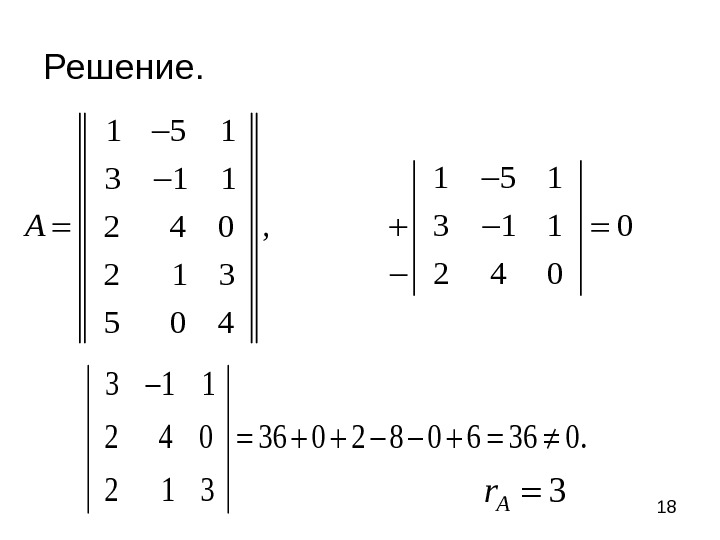
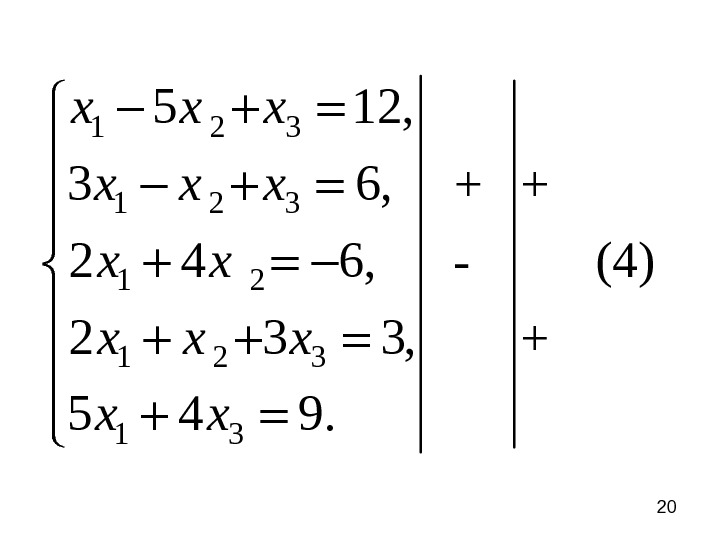

lekciya_4_lineynye_uravneniya_pri_pomoschi_matric.ppt
- Размер: 181.0 Кб
- Автор:
- Количество слайдов: 22
Описание презентации 111 1 12 2 1 1 21 1 по слайдам
 111 1 12 2 1 1 22 2 1 1 2 2. . . . n n n nn n n a x a x a x b Решение системы линейных уравнений при помощи матриц 3 n
111 1 12 2 1 1 22 2 1 1 2 2. . . . n n n nn n n a x a x a x b Решение системы линейных уравнений при помощи матриц 3 n
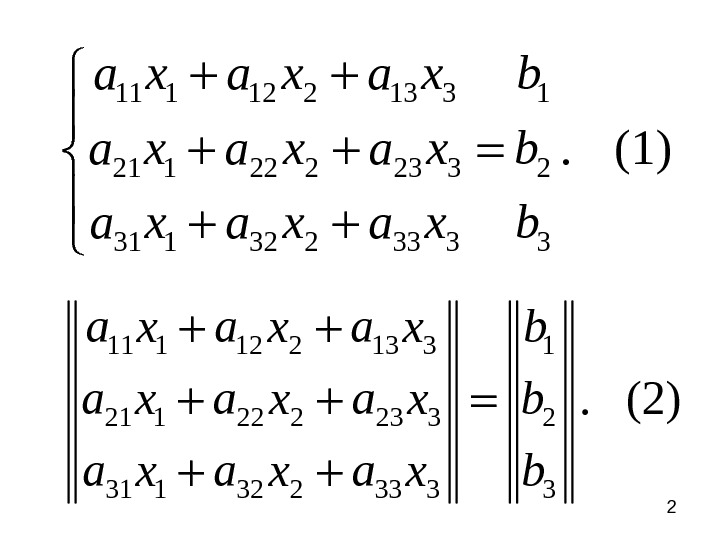 211 1 12 2 13 3 1 21 1 22 2 23 3 2 31 1 32 2 33 3 3. (2)a x a x a x b 11 1 12 2 13 3 1 21 1 22 2 23 3 2 31 1 32 2 33 3 3. (1) a x a x a x b
211 1 12 2 13 3 1 21 1 22 2 23 3 2 31 1 32 2 33 3 3. (2)a x a x a x b 11 1 12 2 13 3 1 21 1 22 2 23 3 2 31 1 32 2 33 3 3. (1) a x a x a x b
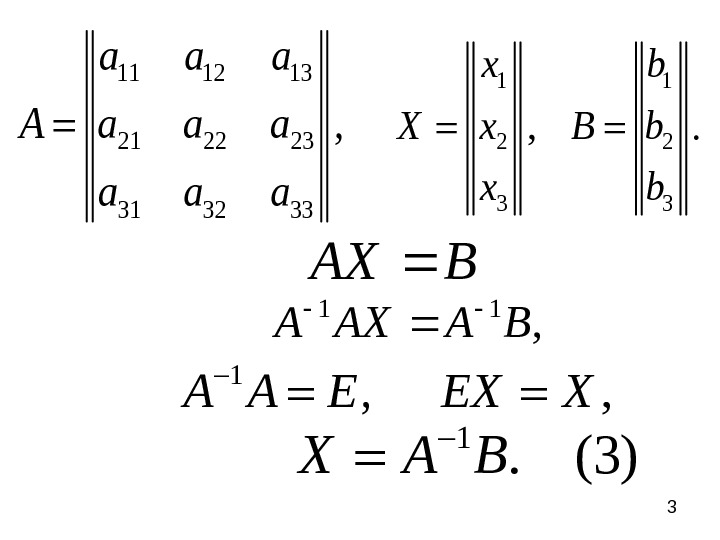 31 1 2 2 3 3 , . x b X x B b x b BAX 11 12 13 21 22 23 31 32 33 , a a a A a a a , 11 BAAXA 1 , , A A E EX X 1. (3)X
31 1 2 2 3 3 , . x b X x B b x b BAX 11 12 13 21 22 23 31 32 33 , a a a A a a a , 11 BAAXA 1 , , A A E EX X 1. (3)X
 4 Пример. Решить систему уравнений с помощью обратной матрицы 1 2 37 2 3 13, 9 3 4 15 , 5 3 14. x x x x x , BAX 7 2 3 9 3 4 ; 5 1 3 A 1 2 3 13 ; 15. 14 x X x B x
4 Пример. Решить систему уравнений с помощью обратной матрицы 1 2 37 2 3 13, 9 3 4 15 , 5 3 14. x x x x x , BAX 7 2 3 9 3 4 ; 5 1 3 A 1 2 3 13 ; 15. 14 x X x B x
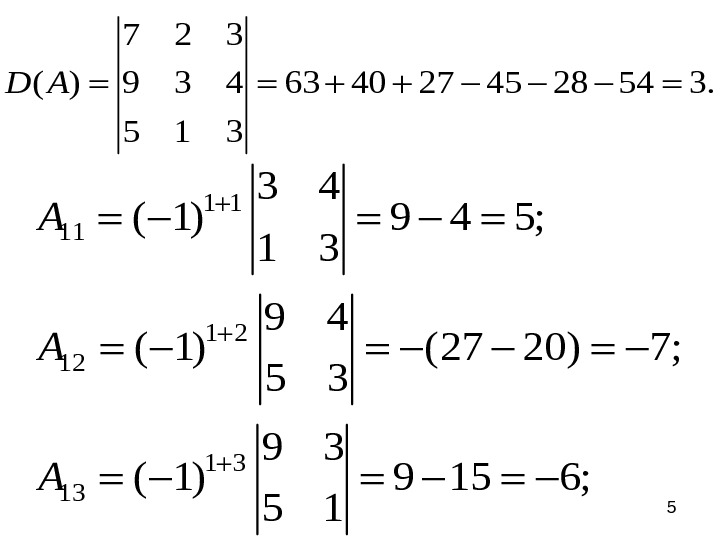 51 1 11 1 2 12 1 3 13 3 4 ( 1) 9 4 5; 1 3 9 4 ( 1) (27 20) 7; 5 3 9 3 ( 1) 9 15 6; 5 1 A A A 7 2 3 ( ) 9 3 4 63 40 27 45 28 54 3.
51 1 11 1 2 12 1 3 13 3 4 ( 1) 9 4 5; 1 3 9 4 ( 1) (27 20) 7; 5 3 9 3 ( 1) 9 15 6; 5 1 A A A 7 2 3 ( ) 9 3 4 63 40 27 45 28 54 3.
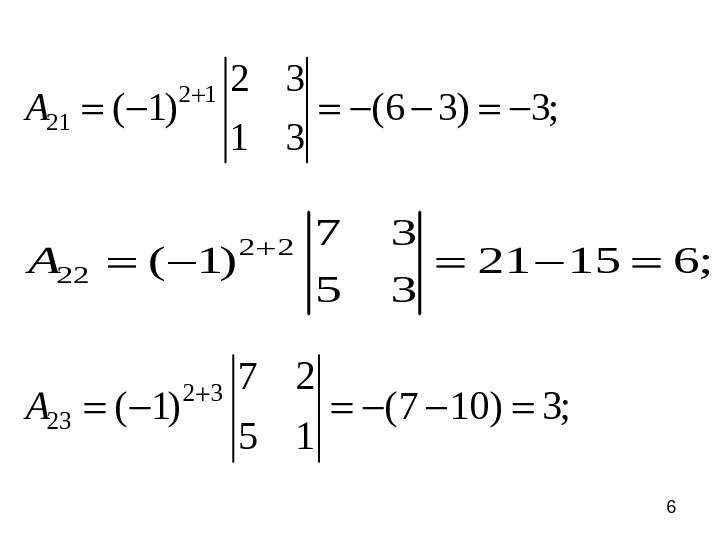 62 2 22 7 3 ( 1) 21 15 6; 5 3 A 2 1 21 2 3 ( 1) (6 3) 3; 1 3 A 2 3 23 7 2 ( 1) (7 10) 3;
62 2 22 7 3 ( 1) 21 15 6; 5 3 A 2 1 21 2 3 ( 1) (6 3) 3; 1 3 A 2 3 23 7 2 ( 1) (7 10) 3;
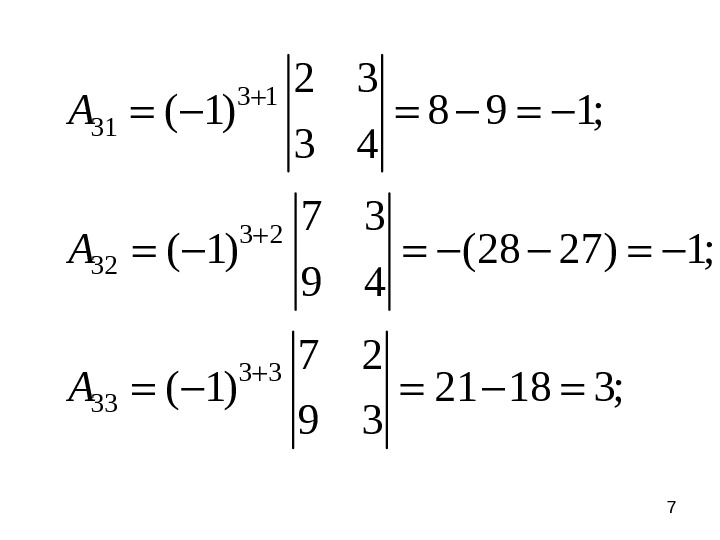 73 1 31 3 2 32 3 3 33 2 3 ( 1) 8 9 1; 3 4 7 3 ( 1) (28 27) 1; 9 4 7 2 ( 1) 21 18 3;
73 1 31 3 2 32 3 3 33 2 3 ( 1) 8 9 1; 3 4 7 3 ( 1) (28 27) 1; 9 4 7 2 ( 1) 21 18 3;
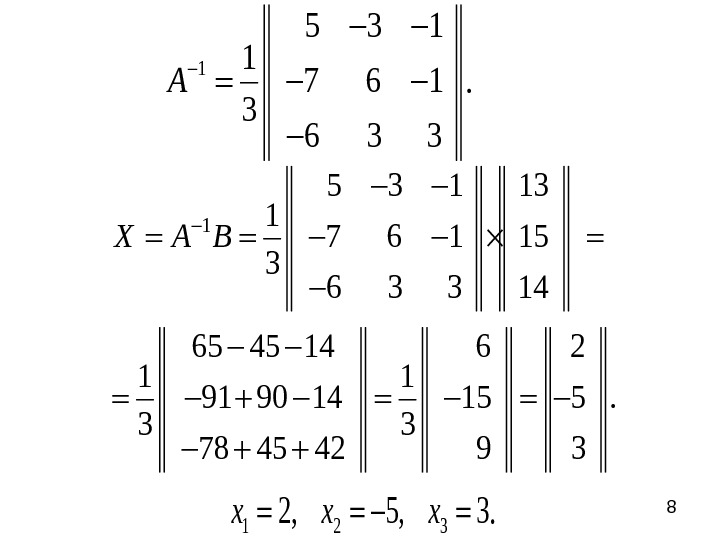
 81 5 3 1 1 7 6 1. 3 6 3 3 A 1 5 3 1 13 1 7 6 1 15 3 6 3 3 14 65 45 14 6 2 1 1 91 90 14 15 5. 3 3 78 45 42 9 3 X A B 1 2 3 2, 5, 3. x x x
81 5 3 1 1 7 6 1. 3 6 3 3 A 1 5 3 1 13 1 7 6 1 15 3 6 3 3 14 65 45 14 6 2 1 1 91 90 14 15 5. 3 3 78 45 42 9 3 X A B 1 2 3 2, 5, 3. x x x
 9 § 10. Произвольные системы линейных уравнений . . . 2211 22222121 11212111 mnmnmm nn nn bxaxaxa ; 21 22221 11211 mnmm n n aaa aaa A mmnmm n n baaa
9 § 10. Произвольные системы линейных уравнений . . . 2211 22222121 11212111 mnmnmm nn nn bxaxaxa ; 21 22221 11211 mnmm n n aaa aaa A mmnmm n n baaa
 10 Определитель квадратной матрицы, содержащей k строк и k столбцов, выбранных произвольным способом, называется минором k -го порядка данной матрицы. Минор первого порядка — это любой элемент матрицы. Рангом матрицы A называется число r такое, что среди миноров r -го порядка данной матрицы имеется по крайней мере один, отличный от нуля, а все миноры ( r+1 ) -го порядка равны нулю.
10 Определитель квадратной матрицы, содержащей k строк и k столбцов, выбранных произвольным способом, называется минором k -го порядка данной матрицы. Минор первого порядка — это любой элемент матрицы. Рангом матрицы A называется число r такое, что среди миноров r -го порядка данной матрицы имеется по крайней мере один, отличный от нуля, а все миноры ( r+1 ) -го порядка равны нулю.
 11 Теорема (критерий Кронекера-Капелли). Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы этой системы был равен рангу ее расширенной матрицы, то есть чтобы Рассмотрим два возможных случая: 1) если , то система уравнений несовместна; 2) если то система уравнений совместна. . BA rr ( ) B A r r , rrr
11 Теорема (критерий Кронекера-Капелли). Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы этой системы был равен рангу ее расширенной матрицы, то есть чтобы Рассмотрим два возможных случая: 1) если , то система уравнений несовместна; 2) если то система уравнений совместна. . BA rr ( ) B A r r , rrr
 12 Совместная система может быть либо определенная, либо неопределенная : а) если ранг матрицы системы равен числу неизвестных , то система имеет единственное решение, которое можно найти по формулам Крамера, б) если ранг матрицы системы меньше числа неизвестных , то система имеет бесконечное множество решений, причем число уравнений в системе необходимо уменьшить до r штук, где r — ранг матрицы системы. )(nr
12 Совместная система может быть либо определенная, либо неопределенная : а) если ранг матрицы системы равен числу неизвестных , то система имеет единственное решение, которое можно найти по формулам Крамера, б) если ранг матрицы системы меньше числа неизвестных , то система имеет бесконечное множество решений, причем число уравнений в системе необходимо уменьшить до r штук, где r — ранг матрицы системы. )(nr
 13 Пример 1. Решить систему линейных уравнений 6778 3455 42 4321 xxxx 1 1 1 2 1 5 5 4.
13 Пример 1. Решить систему линейных уравнений 6778 3455 42 4321 xxxx 1 1 1 2 1 5 5 4.
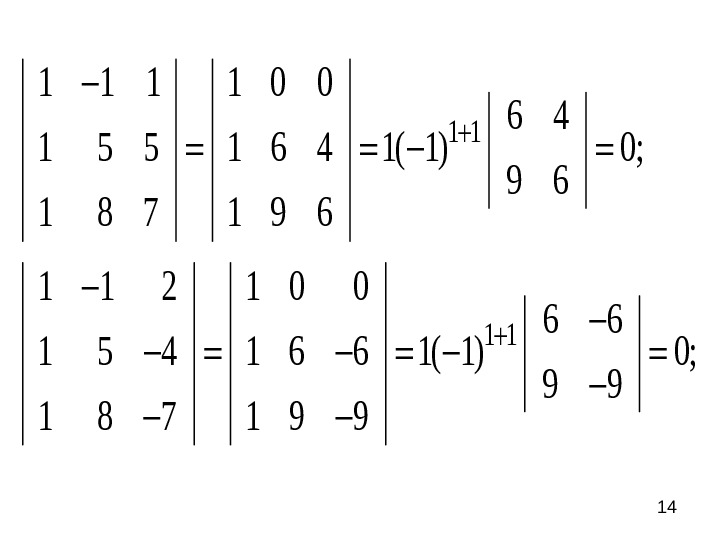 141 1 1 1 0 0 6 4 1 5 5 1 6 4 1( 1) 0; 9 6 1 8 7 1 9 6 1 1 2 1 0 0 6 6 1 5 4 1 6 6 1( 1) 0;
141 1 1 1 0 0 6 4 1 5 5 1 6 4 1( 1) 0; 9 6 1 8 7 1 9 6 1 1 2 1 0 0 6 6 1 5 4 1 6 6 1( 1) 0;
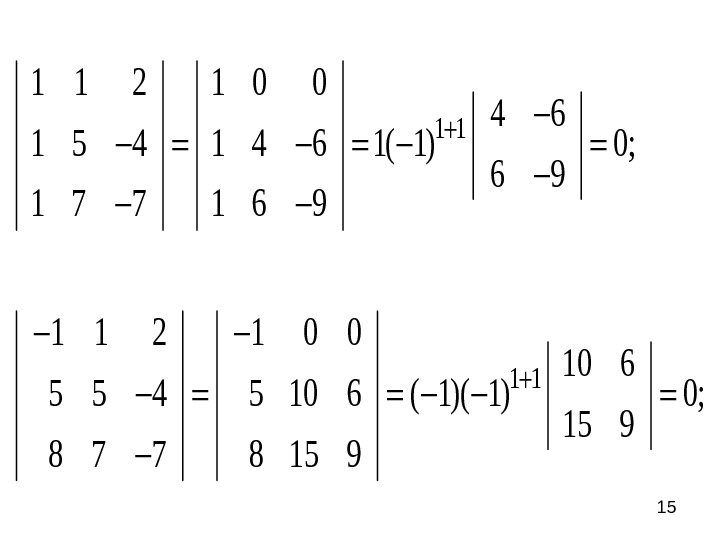 151 1 1 2 1 0 0 4 6 1 5 4 1 4 6 1( 1) 0; 6 9 1 7 7 1 6 9 1 1 2 1 0 0 10 6 5 5 4 5 10 6 ( 1) 0;
151 1 1 2 1 0 0 4 6 1 5 4 1 4 6 1( 1) 0; 6 9 1 7 7 1 6 9 1 1 2 1 0 0 10 6 5 5 4 5 10 6 ( 1) 0;
 161 1 5 2 7 0. 1 5 . 2 A r 1 1 1 2 4 1 5 5 4 3 . 1 8 7 7 6 B 1 1 4 1 5 3 30 3 32 20 24 6 75 0, 1 8 6 . 3 B r B A r r Система несовместна, так как
161 1 5 2 7 0. 1 5 . 2 A r 1 1 1 2 4 1 5 5 4 3 . 1 8 7 7 6 B 1 1 4 1 5 3 30 3 32 20 24 6 75 0, 1 8 6 . 3 B r B A r r Система несовместна, так как
 17 Пример. Решить систему1 2 3 1 3 5 12, 3 6, 2 4 6, (4) 2 3 3, 5 4 9. x x x x
17 Пример. Решить систему1 2 3 1 3 5 12, 3 6, 2 4 6, (4) 2 3 3, 5 4 9. x x x x
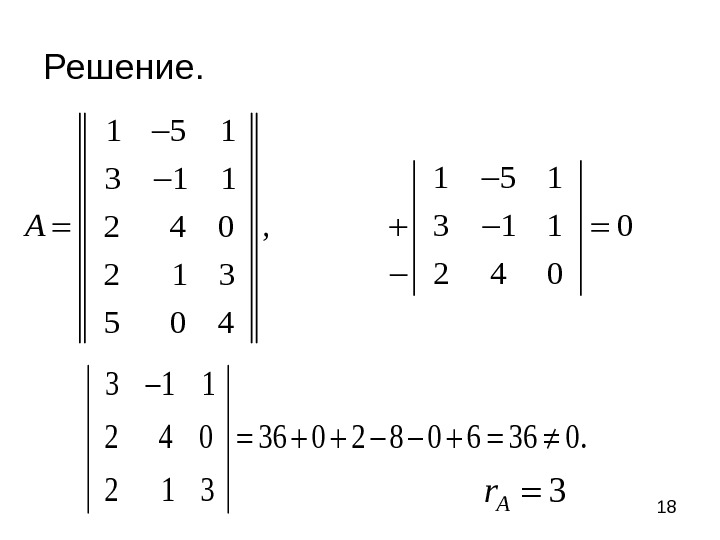 181 5 13 1 1 , 3 1 1 02 4 02 1 3 5 0 4 A 3 1 1 2 4 0 36 0 2 8 0 6 36 0. 2 1 3 3 Ar. Решение.
181 5 13 1 1 , 3 1 1 02 4 02 1 3 5 0 4 A 3 1 1 2 4 0 36 0 2 8 0 6 36 0. 2 1 3 3 Ar. Решение.
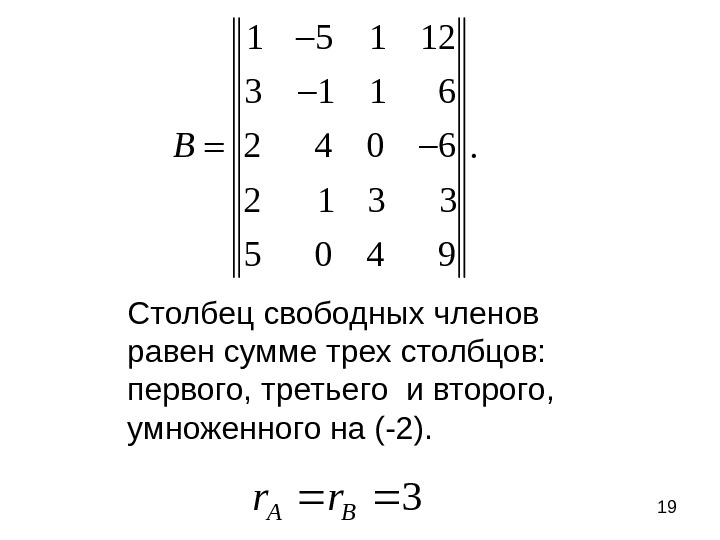
 191 5 1 12 3 1 1 6. 2 4 0 6 2 1 3 3 5 0 4 9 B Столбец свободных членов равен сумме трех столбцов: первого, третьего и второго, умноженного на (-2). 3 BA rr
191 5 1 12 3 1 1 6. 2 4 0 6 2 1 3 3 5 0 4 9 B Столбец свободных членов равен сумме трех столбцов: первого, третьего и второго, умноженного на (-2). 3 BA rr
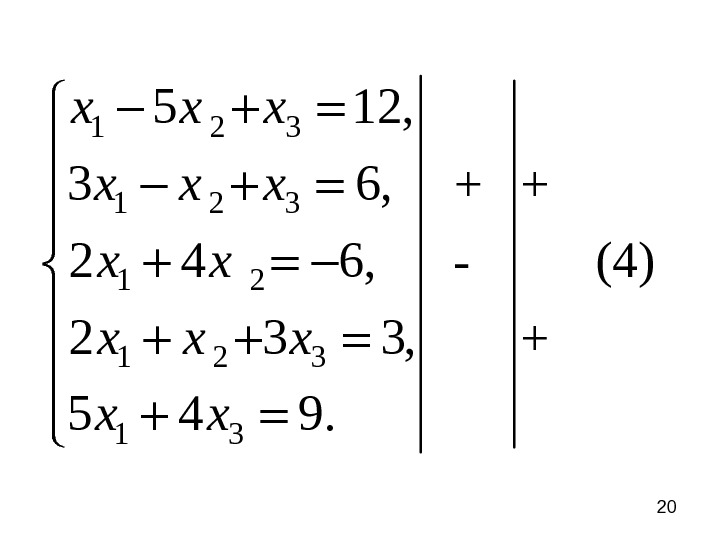 201 2 3 1 3 5 12, 3 6, + + 2 4 6, (4)- 2 3 3, + 5 4 9. x x x x
201 2 3 1 3 5 12, 3 6, + + 2 4 6, (4)- 2 3 3, + 5 4 9. x x x x
 21 Система совместна и имеет единственное решение, так как 3 r n 1 2 3 3 6, 2 4 6, 2 3 3. x x x x
21 Система совместна и имеет единственное решение, так как 3 r n 1 2 3 3 6, 2 4 6, 2 3 3. x x x x
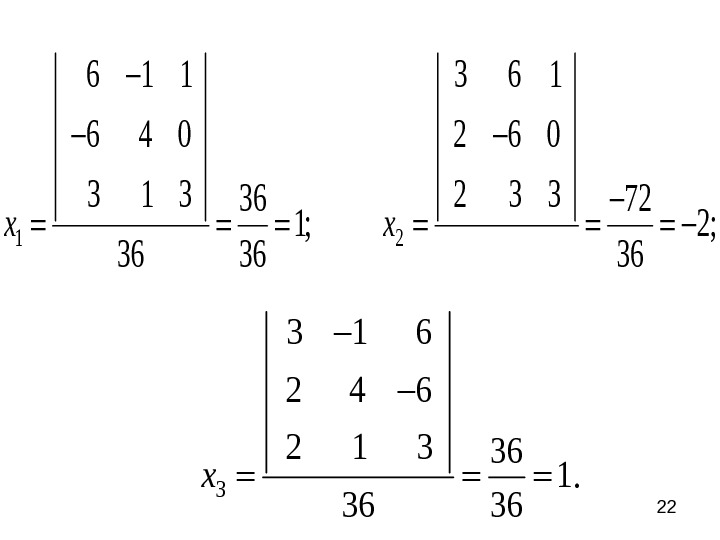
 221 2 6 1 1 3 6 1 6 4 0 2 6 0 3 1 3 2 3 336 72 1; 2; 36 36 36 x x 3 3 1 6 2 4 6 2 1 336 1. 36 36 x
221 2 6 1 1 3 6 1 6 4 0 2 6 0 3 1 3 2 3 336 72 1; 2; 36 36 36 x x 3 3 1 6 2 4 6 2 1 336 1. 36 36 x

