1 Управление инвестиционным портфелем Модели риска 2

1 Управление инвестиционным портфелем Модели риска

2 Риск в финансах • Бизнес риск • Финансовый риск – рыночный риск – кредитный риск – риск ликвидности • Операциональный риск • Правовой риск

3 Две замечательные книги • Бернстайн П. «Против Богов: Укрощение риска» , М. : Олимп-Бизнес, 2006. • Талеб Нассим «Одураченные случайностью» М. : Интернет-трейдинг, 2002.

4 Основные теоретико-вероятностные понятия

5 Основные теоретико-вероятностные и статистические понятия • Определенность и неопределенность • Вероятности и распределения случайных величин. • Среднее (матожидание) , вариация • Многомерные распределения • Ковариация , корреляция , бета • Квантили

6 Вероятность Определенность Неопределенность Вероятность выпадения заданного числа очков при бросании кости Р( « 5» ) =1/

7 Вероятность Элементарные события 1 , 2 , … , n Пространство элементарных событий : = { 1 , 2 , … , n } События – произвольное множество элементарных событий А = { i 1 , i 2 , … , ik }

8 Вероятность Вероятности элементарных событий р1 = р ( 1 ), р2 = р ( 2 ), … , рn = р ( n ) Вероятность события – сумма вероятностей элементарных событий: А = { i 1 , i 2 , … , i k } Р( А ) = р ( i 1 ) + р ( i 2 ) +…+ р ( ik ),

9 Вероятностное пространство 1) Пространство элементарных событий : = { 1 , 2 , … , n } 2) Вероятности элементарных событий р : R, р ( k ) 0, k =1, …, n. р ( 1 ) + р ( 2 ) +…+ р ( n ) = 1 2) Класс всех событий

10 Вероятность. Пример Бросание монеты. Элементарные события: 1 = «Орел» 2 , = «Решка» Пространство элементарных событий : = { О; Р } Событие – выпадение орла А = { О }

11 Вероятность. Пример Бросание монеты. Вероятности элементарных событий: Р( «Орел» )= Р( «Решка» ) = 1/2 Событие – выпадение орла А = { О } ; P( A )=1/2 Событие – выпадение орла или решки А = { О; Р } = ; P( A )= P( )= 1/2+ 1/2 =

12 Вероятность. Пример Бросание правильной кости. Элементарные события: 1 = « 1» , 2 = « 2» , 3 = « 3» , 4 = « 4» , 5 = « 5» , 6 = « 6» , Пространство элементарных событий : = { 1; 2; 3; 4; 5; 6 } Событие А : выпадение четного числа очков А = { 2; 4; 6 }

13 Вероятность. Пример Бросание правильной кости. Вероятности элементарных событий: p ( « 1» ) = p ( « 2 » ) = … = p ( « 6 » ) =1/6 Событие А : выпадение четного числа очков А = { 2; 4; 6 } P( A )= p ( « 2 » ) + p ( « 4 » ) + p ( « 6 » ) =3/6 =1/

14 Пример Бросание двух правильных костей Какова вероятность выпадения в сумме пяти очков Вероятности выпадения произвольной пары очков одинаковы Все элементарные события равновероятны

15 Пример ( продолжение ) Сумма числа очков при бросании двух костей Пример = ( 4 ; 1 ) S = 4 + 1 = 5, вероятность (1/6) ( 1/6) = 1/

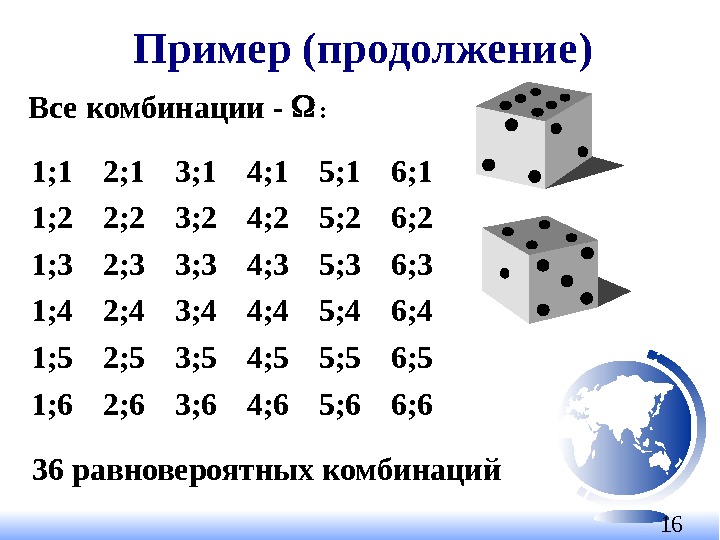
16 Пример ( продолжение ) 1 ; 1 2 ; 1 3; 1 4; 1 5; 1 6; 1 1; 2 2; 2 3; 2 4; 2 5; 2 6; 2 1; 3 2; 3 3; 3 4; 3 5; 3 6; 3 1; 4 2; 4 3; 4 4; 4 5; 4 6; 4 1; 5 2; 5 3; 5 4; 5 5; 5 6; 5 1; 6 2; 6 3; 6 4; 6 5; 6 6; 6 Все комбинации — : 36 равновероятных комбинаций

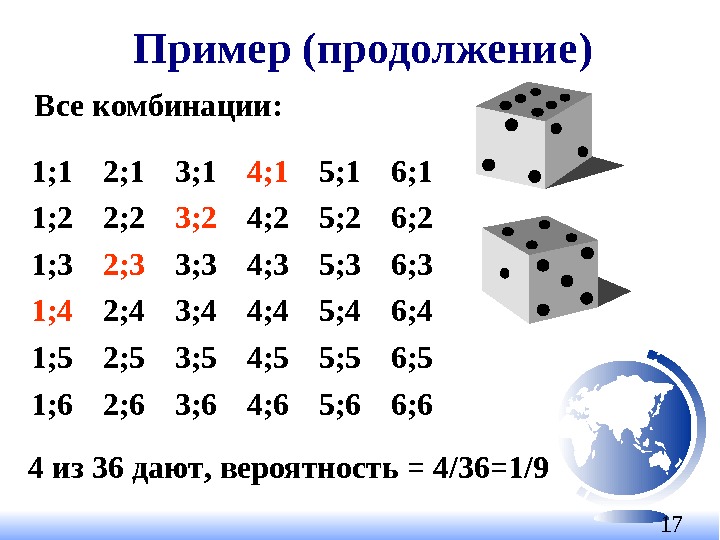
17 Пример ( продолжение ) 1; 1 2; 1 3; 1 4; 1 5; 1 6; 1 1; 2 2; 2 3; 2 4; 2 5; 2 6; 2 1; 3 2; 3 3; 3 4; 3 5; 3 6; 3 1; 4 2; 4 3; 4 4; 4 5; 4 6; 4 1; 5 2; 5 3; 5 4; 5 5; 5 6; 5 1; 6 2; 6 3; 6 4; 6 5; 6 6; 6 Все комбинации : 4 из 36 дают , вероятность = 4/36= 1/

18 Случайная величина Величина X значения (реализации) которой зависят от случайных событий Формально это функция (отображение) на вероятностном пространстве X: R X( ) R – значение сл. в.

19 Случайная величина Дискретная случайная величина принимает конечное (или счетное ) число значений x 1 , x 2 , … , x m , … Непрерывная случайная величина принимает континуум значений (значения могут заполнять весь промежуток числовой оси R)

20 Случайная величина. Пример Сумма X очков при одновременном бросании двух костей X = X 1 + X 2 X 1 и X 2 – число очков на первой и второй кости

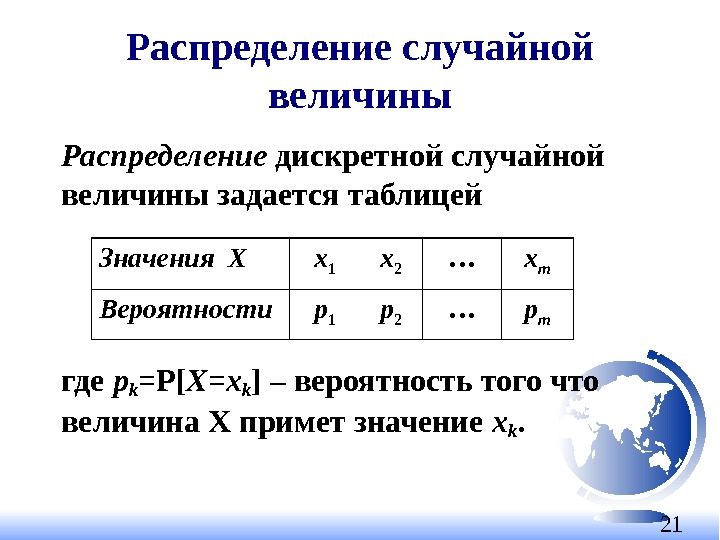
21 Распределение случайной величины Распределение дискретной случайной величины задается таблицей где pk =P[ X = xk ] – вероятность того что величина Х примет значение x k. Значения Х x 1 x 2 … x m Вероятности p 1 p 2 … p m

22 Распределение случайной величины Распределение суммы очков на двух гранях при бросании двух костей Например P( X =4)=P({(1; 3), (2; 2), (3; 1)})= 3/36 =1/12 Значения Х 2 3 4 … 12 12 Вероятности 1/36 2/36 3/36 … 2/36 1/

23 Случайная величина. Пример Непрерывная случайная величина X. Стрельба в мишень. Значения — расстояние от точки попадания до центра мишени X

24 Характеристики случайных величин Среднее Вариация (дисперсия)

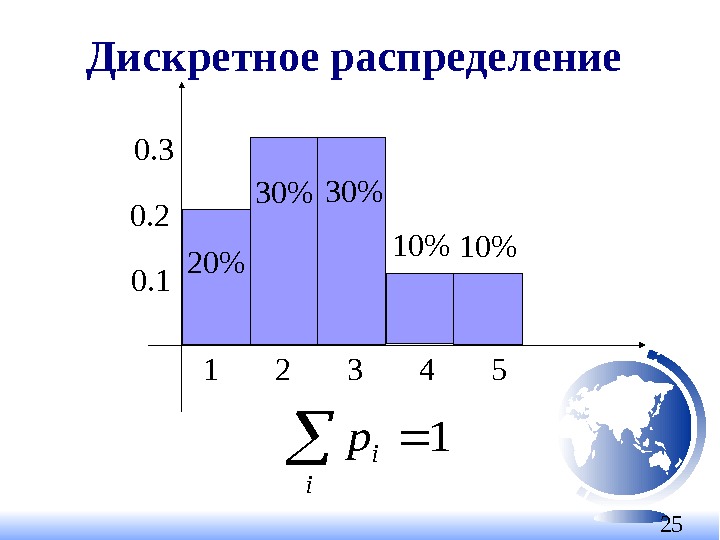
25 Дискретное распределение 1 2 3 4 50. 2 0. 3 0. 1 20% 30% 10% i i p

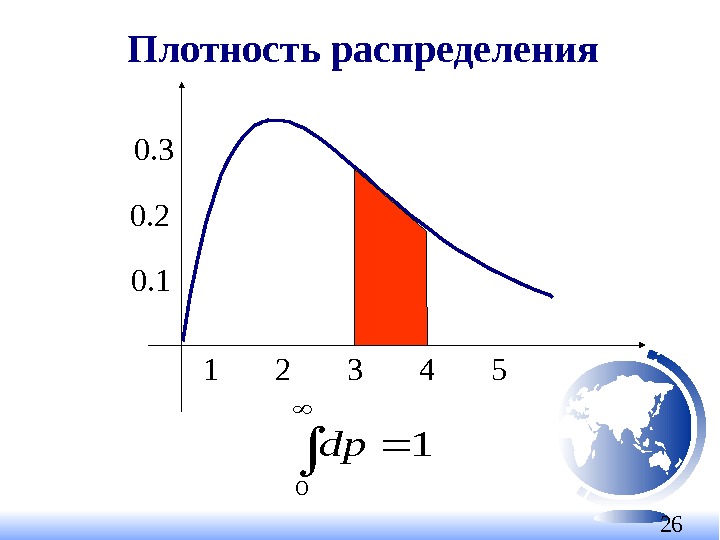
26 Плотность распределения 1 2 3 4 50. 2 0. 3 0. 11 0 dp

27 Характеристики дискретных случайных величин Дискретная случайная величина X : = { 1 , 2 , … , n } R Математическое ожидание (среднее) величины Х : m X = E[ X ] = = = X ( 1 ) p ( 1 ) + X ( 2 ) p ( 2 ) +…+ X( n ) p ( n ) )()ω(ω Ωω p. X

28 Характеристики дискретных случайных величин Если дискретная случайная величина имеет распределение то ее математическое ожидание равно E[ X ] = x 1 p 1 + x 2 p 2 +…+ xn pn Значения Х x 1 x 2 … x m Вероятности p 1 p 2 … p m

29 Характеристики дискретных случайных величин. Пример Пусть Х — число выпавших очков при бросании кости. Распределение Х имеет вид Математическое ожидание m X сл. в. Х равно E[ X ] = 1 1/6 + 2 1/6 + 3 1/6 + 4 1/6 + 5 1/6 + 6 1/6 = = (1+2+3+4+5+6)/6 = (6 7/2)/6 = 3, 5 Значения Х 1 2 3 4 5 6 Вероятности 1/6 1/6 1/

30 Характеристики дискретных случайных величин Вариация дискретной случайной величины X : = { 1 , 2 , … , n } R Var [ X ] = E[ X — m X ]2 = E[ X 2 ] — (E[ X ])2 = где m X = E[ X ] – математическое ожидание Х. По распределению сл. в. Х вариация находится по формуле Var [ X ] = ( х 1 — m. X )2 p 1 + ( х2 — m. X )2 p 2 +…+ ( хn — m. X )2 pn

31 Характеристики дискретных случайных величин Стандартное отклонение – квадратный корень из вариации ( X ) = Var [ X ] Стандартное отклонение имеет размерность самой случайной величины

32 Характеристики дискретных случайных величин. Пример Пусть Х — число выпавших очков при бросании кости. m X = E[ X ]=3, 5 Вариация Х равна Var [ X ] = (1 -3, 5) 2 1/6 + (2 -3, 5) 2 1/6+ (3 -3, 5) 2 1/6 + + (4 -3, 5) 2 1/6 + (5 -3, 5) 2 1/6 + (1 -3, 5) 2 1/6 = = (1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 )/6 – (3, 5) 2 = 2, 92 Стандартное отклонение ( X ) = 2, 92 = 1,

33 Непрерывные распределения Xdp. Xсреднее dp. XXXВариация 22 )()( )(XВариация

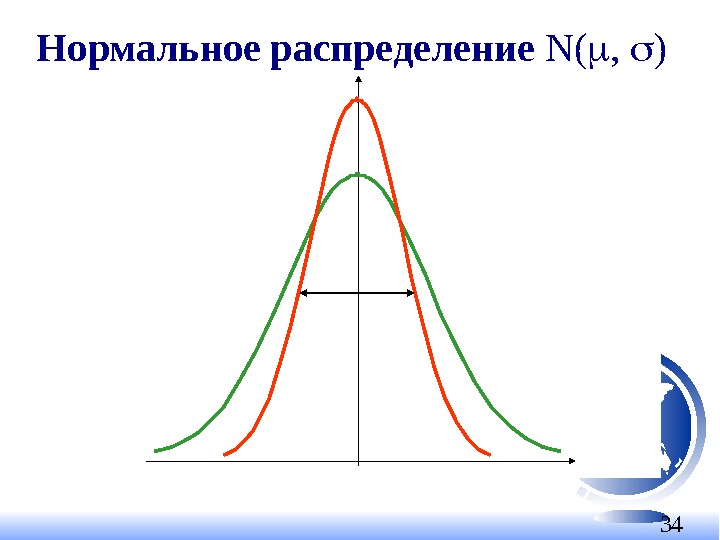
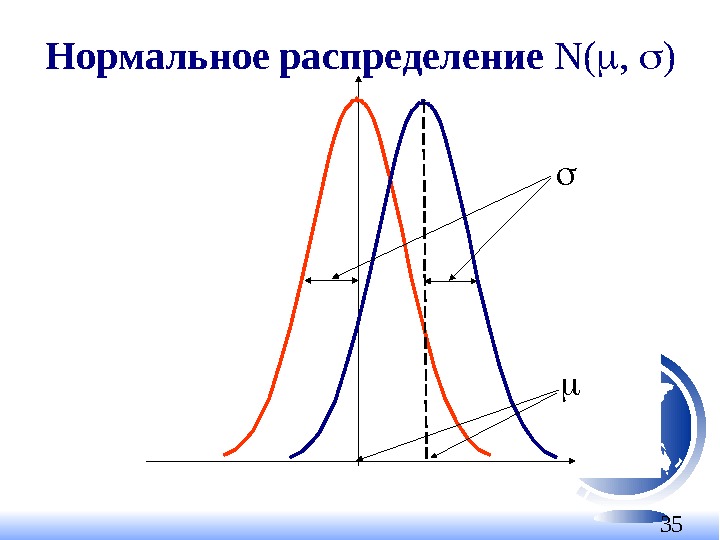
34 Нормальное распределение N( , )

35 Нормальное распределение N( , )

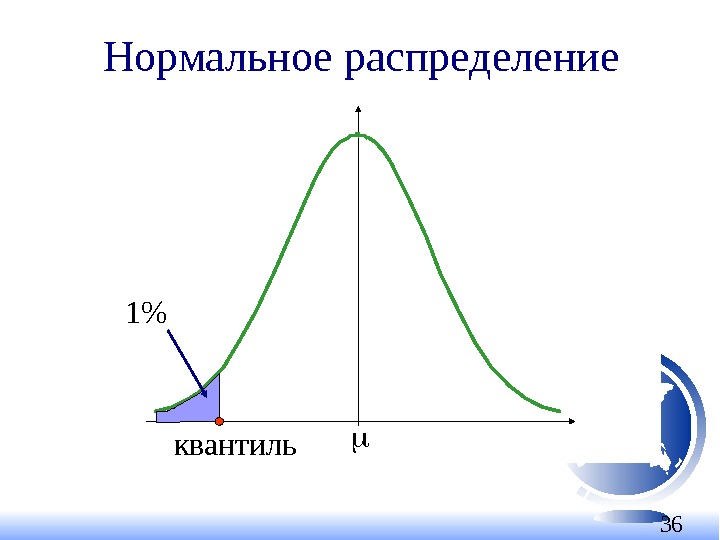
36 Нормальное распределение квантиль1%

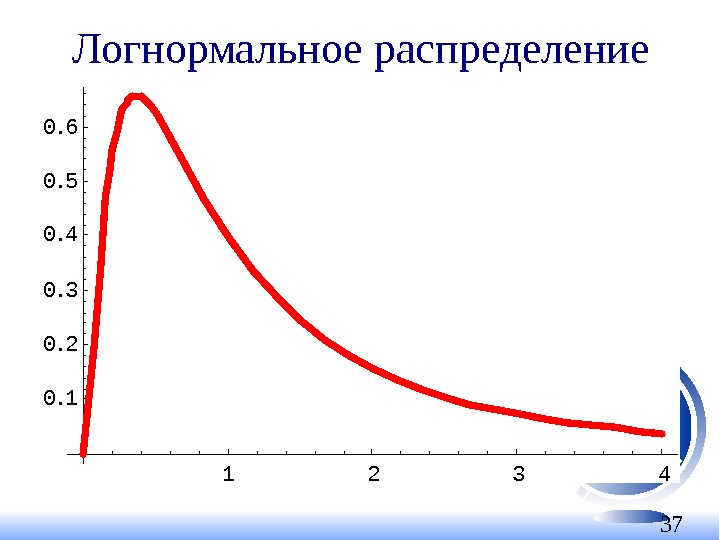
37 Логнормальное распределение 1234 0. 1 0. 2 0. 3 0. 4 0. 5 0.

38 Свойства математического ожидания • Математическое ожидание –линейная функция : E( X 1 + X 2 ) = E( X 1 ) + E( X 2 ) E( a. X ) = a E( X ) • В общем случае E( a 1 X 1 + a 2 X 2 + …+ a n X n ) = = a 1 E( X 1 ) + a 2 E( X 2 ) +…+ a n E( X n ) • X = const E( X ) = E( c ) = c

39 Статистические оценки • На практике пространство элементарных событий как правило неизвестно , неизвестны и элементарные вероятности. • Поэтому характеристики случайных величин получаются не из теоретических формул • Параметры сл. в. оцениваются исходя из серии наблюдений над значениями сл. в. по так называемой выборке.

40 Статистические оценки • Выборка последовательность значений сл. в. Х полученных в результате опыта наблюдения или эксперимента: x 1 , x 2 , …, x. N — выборка объема N.

41 Выборка. Пример • Пусть кость бросается 10 раз. В Результат бросания 10 чисел: 5, 2, 4, 6, 3, 2, 1, 5 , 3 — выборка объема 10.

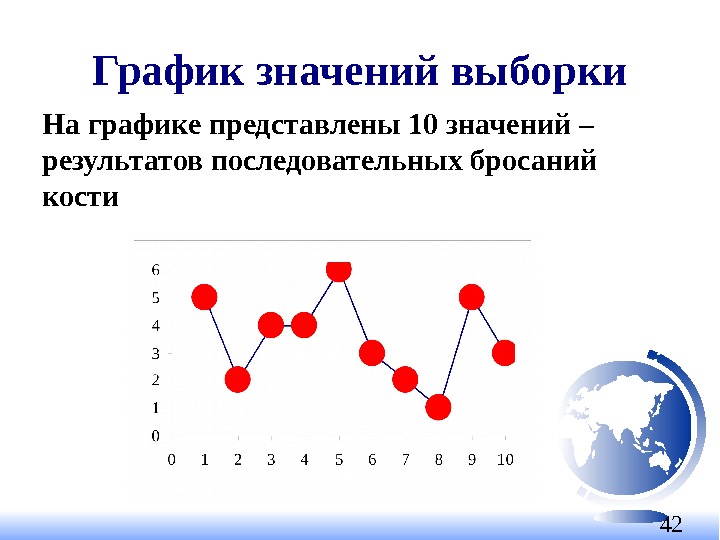
42 График значений выборки На графике представлены 10 значений – результатов последовательных бросаний кости

43 Выборочные (статистические) оценки • Оценки параметров сл. в. по выборке тем точнее чем больше объем выборки т. е. объем статистических данных • Наиболее часто используются оценку математического ожидания , вариации (дисперсии) и среднеквадратичного отклонения

44 Выборочное среднее – Выборочное среднее есть просто среднее арифметическое наблюдаемых значений – Допустим что у нас есть 5 -летняя выборка из 60 месячных доходностей r 1 , r 2 , …, r 60 некоторой акции – Тогда выборочное среднее вычисляется по формуле N x. . . xx x N 21 60 6021 r . . . r r

45 Выборочная вариация – Выборочная дисперсия вычисляется по формуле где х — выборочное среднее. Заметим что знаменатель формулы на 1 меньше числа наблюдений. 1 N xx. . . xxxx s N 22 2 2 12)()()(

46 Выборочное среднее и вариация. Пример Рассмотрим снова результат 10 -кратного бросания кости: 5, 2, 4, 6, 3, 2, 1, 5 , 3 Выборочное среднее х = (5 + 2 + 4 + 6 + 3 + 2 + 1 + 5 + 3 )/10 = 3, 5 Выборочная вариация s 2 =[(5 -3, 5)2 +(2 -3, 5)2 +(4 -3, 5)2 +(6 -3, 5)2 + (3 -3, 5) 2 +(2 -3, 5)2 +(1 -3, 5)2 +(5 -3, 5)2 +(3 -3, 5)2 ]/9=2,

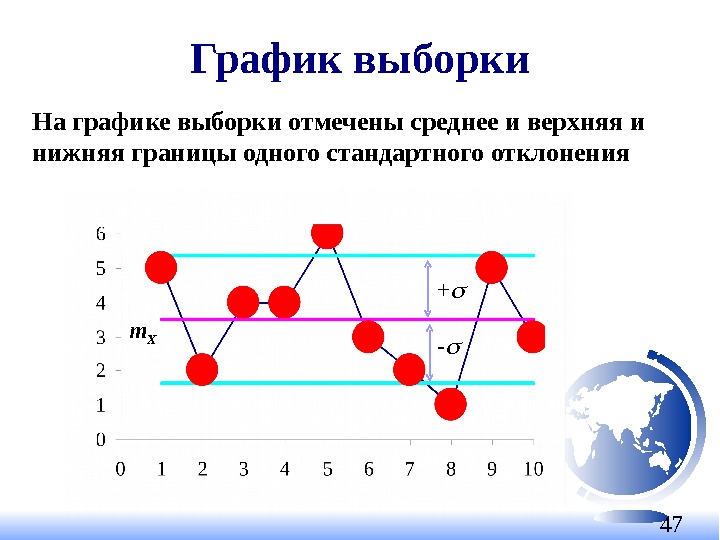
47 График выборки На графике выборки отмечены среднее и верхняя и нижняя границы одного стандартного отклонения m X + —

48 Выборочные (статистические) оценки – Среднее, вариация и стандартное отклонение ( как и распределение ) могут меняться со временем – Поэтому нужно с осторожностью относиться к получаемым статистическим оценкам

49 Связи меду случайными величинами • В финансовом анализе часто приходится работать не с одной, а с несколькими случайными величинами • Например при построении оптимального портфеля нужно учитывать характеристики доходностей всех активов составляющих портфель • Поэтому приходится использовать характеристики взаимной связи случайных величин

50 Ковариация Пусть на вероятностном пространстве определены две случайные величины X и Y X , Y : R Ковариацией этих величин называется число cov( X , Y )= E[( X — E[ X ])( Y — E[ Y ])]= = E[( X — m X )( Y — m Y )] ))()()((), cov(YXm. Ym. XYX

51 Ковариация случайной величины с самой собой равна ее вариации cov(X, X) = Var(X)

52 Совместное распределение Если вероятностное пространство то характеристики связи случайных величин находят по их совместному распределению Пусть X и Y дискретные случайные величины, причем X принимает значения х1 , х2 , …, хm а Y соответственно у 1 , у2 , …, уn

53 Совместное распределение Тогда совместное распределение случайных величины Х и У описывается таблицей вида Где p kj = P[ Х = х k , У = у i ] – вероятность одновременной реализации значения х k величины Х и значения у i величины Уу 1 у 2 … у n х 1 p 12 … p 1 n х 2 p 21 p 22 … p 2 n … х m p m 1 p m 2 … p mn

54 Совместные распределения и ковариация Если случайные величины Х и У определяются совместным распределением , то формула для ковариации имеет вид = ( где х = E[ X ] и y = E[ Y ] – средние значения величин X и Y ) ijpyyxx. X, Yj m, n 1 ji i))(()cov( ,

55 Ковариация служит мерой совместного рассеяния случайных величин вокруг их средних значений В то же время ковариация есть мера связи или взаимного влияния случайных величин Более точной мерой связи между случайными величинами является корреляция точнее коэффициент корреляции

56 Корреляция – это нормированная ковариация Здесь — стандартные отклонения сл. в. Х и У. σ(Y)σ(X), σ(X)σ(Y) cov(X, Y) ρcor(X, Y) YX,

57 Корреляция -1 1 = 0 независимость , т. е. сл. в. Х и У -независимы = 1 совершенная положительная корреляция = -1 совершенная отрицательная корреляция )()(YX YYXXE XY

58 Свойства вариации • Var ( a. X ) = a 2 Var ( X ) • X=c =const Var ( X ) =Var ( c ) = 0 • Если Х и У – независимы Var ( X + Y ) = Var ( X ) + Var ( Y ) • В общем случае Var ( X + Y ) = Var ( X ) + Var ( Y ) + 2 cov ( X, Y )

59 Свойства вариации • Вариация линейной комбинации случайных величин X = a 1 X 1 + a 2 X 2 + … + an Xn Var ( X ) = a 12 Var ( X 1 ) + a 22 Var ( X 2 ) +…+ an 2 Var ( Xn ) + + 2 a 1 a 2 cov( X 1 , X 2 )+…+ 2 a 1 an cov( X 1 , Xn )+ + 2 a 3 cov( X 2 , X 3 )+…+ 2 an cov( X 2 , Xn )+… … + 2 a n-1 an cov( Xn-1 , Xn ) n 1 ji, jiji n 1 k kk)Xcov(Xaa. Xa. Var

60 Свойства стандартного отклонения • ( a. X ) = a ( X ) • Если X=c =const , то ( X ) = ( c ) = 0 • Если Х и У – независимы ( X + Y ) = ( X ) + ( Y ) • В общем случае ( X + Y ) = ( X ) + ( Y ) + 2 XY ( X ) ( Y )

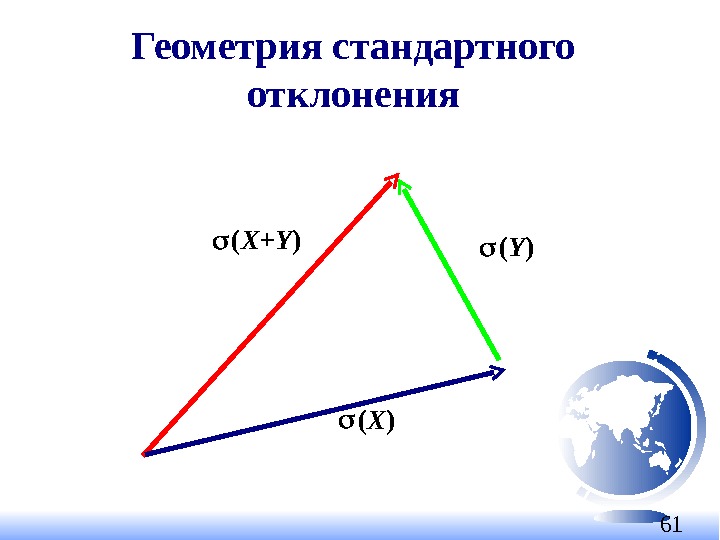
61 ( X+Y ) ( X ) ( Y )Геометрия стандартного отклонения

62 Выборочная ковариация Пусть мы имеем N совместных наблюдений над случайными величинами X и Y : ( x 1 , y 1 ), ( x 2 , y 2 ), …, ( x. N , y. N ). Тогда выборочная ковариация вычисляется по формуле ( X , Y ) = [( x 1 — x )( y 1 — y )+( x 2 — x )( y 2 — y ) + …+ + ( x N — x )( y. N — y )]/( N -1) где x и y – выборочные средние значения величин X и Y.

63 Выборочная корреляция Пусть мы имеем N совместных наблюдений над случайными величинами X и Y : ( x 1 , y 1 ), ( x 2 , y 2 ), …, ( x. N , y. N ). Выборочная корреляция определяется по выборочной корреляции (Y)σ(X)σ (X, Y)σ ρYX,

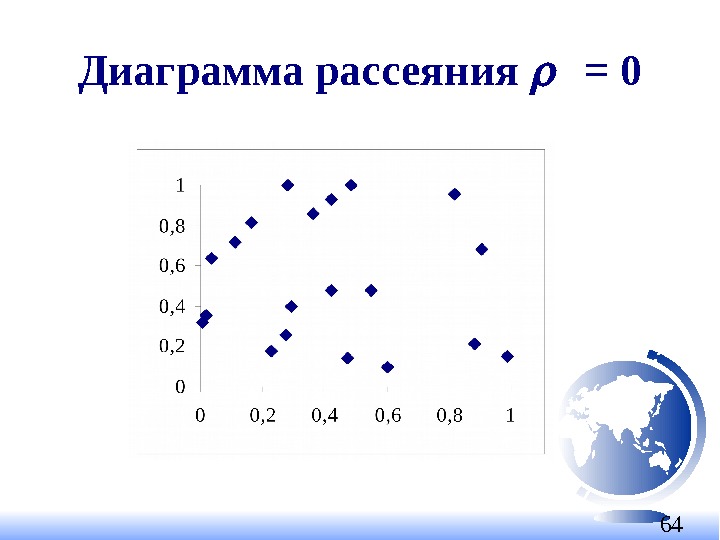
64 Диаграмма рассеяния =

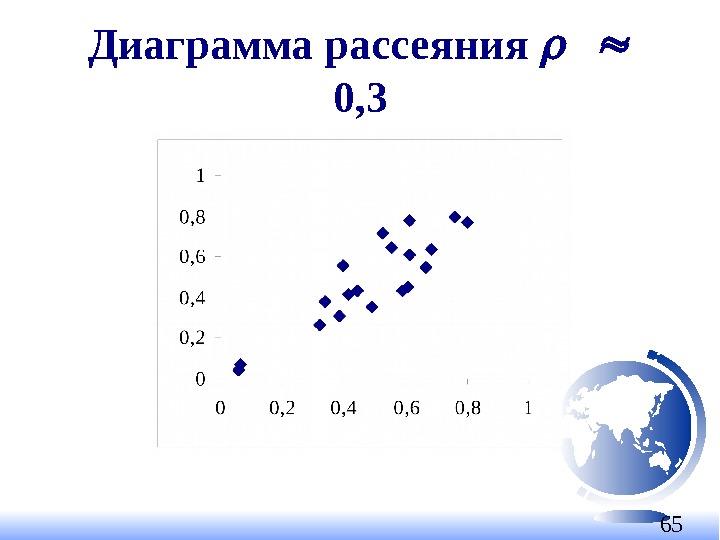
65 Диаграмма рассеяния 0,