1 ТЕОРИЯ МНОЖЕСТВ СТРУКТУРЫ (РЕШЕТКИ). ИЗОМОРФИЗМ. СИСТЕМАТИЗАЦИЯ ВВЕДЕННЫХ

1 ТЕОРИЯ МНОЖЕСТВ СТРУКТУРЫ (РЕШЕТКИ). ИЗОМОРФИЗМ. СИСТЕМАТИЗАЦИЯ ВВЕДЕННЫХ ПОНЯТИЙ ЛЕКЦИЯ 6 Факультет компьютерной инженерии и управления, кафедра АПВТ, ХНУРЭ Лектор – д.т.н., проф. Хаханов В.И. ДИСКРЕТНАЯ МАТЕМАТИКА

2 Цель лекции – изучить свойства структур, выявить взаимосвязи между введенными понятиями Содержание: Определение структуры Подрешетка, интервал, сравнимые элементы, структурные ноль и единица Дедекиндовы (модулярные) решетки Дистрибутивные решетки Изоморфизм множеств, алгебр Алгебраические системы. Модели Схема взаимосвязей между понятиями Тема: Структуры (решетки). Изоморфизм

3 Литература Горбатов В.А. Основы дискретной математики. М.: Высш. шк., 1986. 12-14 с. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Наука, 1984. С. 4-10. Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. 23-25 с. Дискретная математика: Гипертекстовые учебные материалы (электронный учебник) / В.И. Хаханов, С.В. Чумаченко. 2004. http/…/10.13.20.100/nserv/library/ education/Чумаченко/Дискретная математика/ Дистанционный_учебник/index.htm.

4 Термины Базовые понятия: множество, подмножество, бинарное отношение, упорядоченное множество, операции (объединение, пересечение), законы (ассоциативный, коммутативный, элиминации), алгебра Ключевые слова: структура (решетка), дедекиндова (модулярная) решетка, дистрибутивная решетка, подрешетка, изоморфизм

5 Def: Решетка – частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет единственные точную верхнюю (sup) и точную нижнюю (inf) грани Решетка (структура) – это алгебраическая система , для элементов которой справедливы законы: xx=x, xx=x; xy=yx, xy=yx; x(xy)=x, x(xy)=x, и  x,yM ! sup{x,y}=xy, inf{x,y}=xy Рассматриваемая система не является решеткой, если не существуют супремум или инфимум, либо они не единственны Структуры иллюстрируются диаграммами Определение структуры

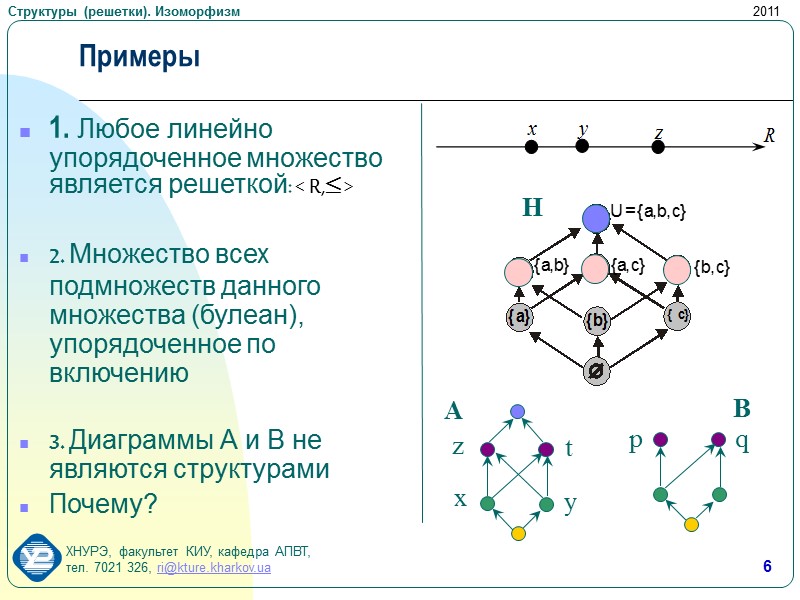
6 Примеры 1. Любое линейно упорядоченное множество является решеткой: < R, > 2. Множество всех подмножеств данного множества (булеан), упорядоченное по включению 3. Диаграммы А и В не являются структурами Почему? В p q

7 Решетка как универсальная алгебра Решетка – универсальная алгебра с двумя бинарными операциями ,  (+, •; ,), удовлетворяющими свойствам: xx=x, xx=x; xy=yx, xy=yx; x(xy)=x, x(xy)=x; x(yz)=(xy)z, x(yz)=(xy)z  x,yM: xy ! sup{x,y}=xy=y, inf{x,y}=xy=x Понятие решетки относится к середине XIX в. Впервые его ввел немецкий математик Дедекинд. Термин «решетка» принадлежит американскому ученому Гаррету Биркгофу из Принстонского университета.

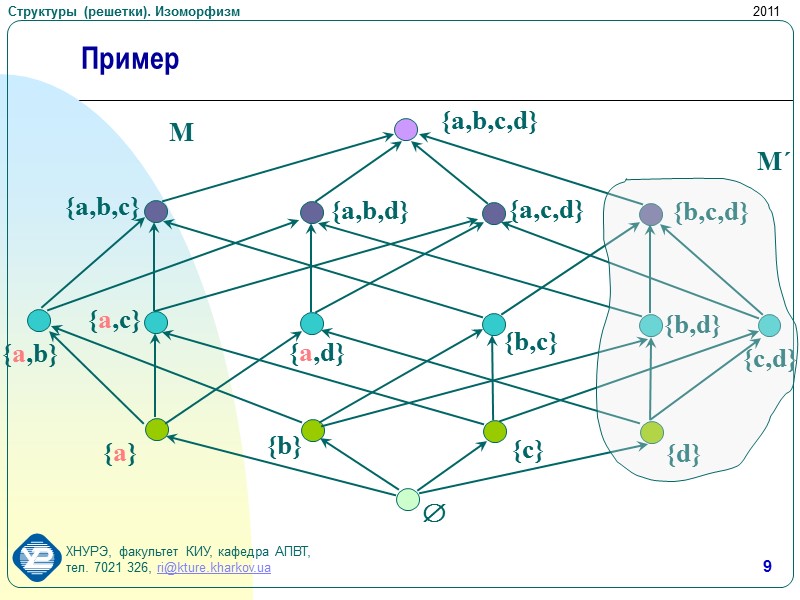
8 Определения Def: Подрешетка M´: M´M:  x,yM´ sup{x,y}M´, inf{x,y}M´ Def: Интервал I=[ma,mb] – подрешетка M´ с наименьшим элементом ma и наибольшим элементом mb: I=[ ma, mb ]={ mM´ | mammb } Def: Нулевой и единичный элементы в решетке называются структурными нулем и единицей. Def: дополнительные элементы xy=1, xy=0 х – дополнение элемента у в решетке : x=y, y=x Def: два элемента, обладающие общим дополнением в решетке, называются связанными Def: два элемента в структуре сравнимы, если в диаграмме их можно соединить путем из стрелок

9 Пример

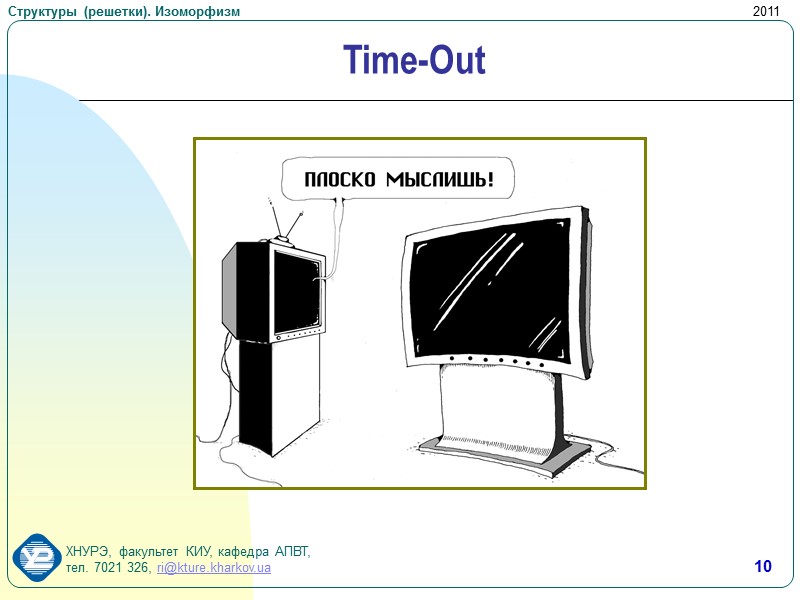
10 Time-Out

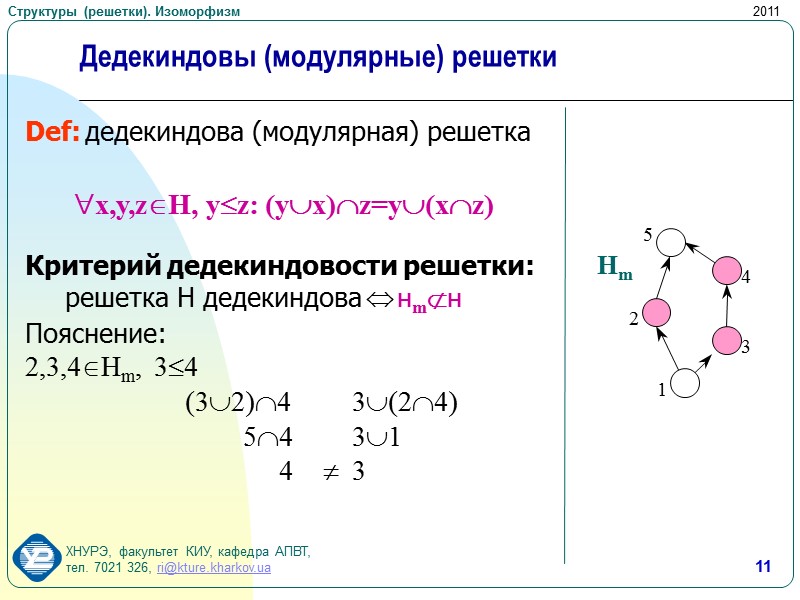
11 Дедекиндовы (модулярные) решетки Def: дедекиндова (модулярная) решетка x,y,zH, yz: (yx)z=y(xz) Критерий дедекиндовости решетки: решетка Н дедекиндова  HmH Пояснение: 2,3,4Hm, 34 (32)4 3(24) 54 31 4  3

12 Историческая справка Немецкий математик Член Берлинской, парижской и Римской Академий наук Родился в Брауншвейге Учился в Геттингенском университете Профессор Высшей технической школы в Брауншвейге Дал теоретико-множественное обоснование теории действительных чисел Ввел теоретико-множественное понятие отображения Разработал основы теории структур С его именем связаны многочисленные математические утверждения и термины: кольцо, поле, структура, сечение, функция Дедекинд Рихард Юлиус Вильгельм (XIX-XXвв.)

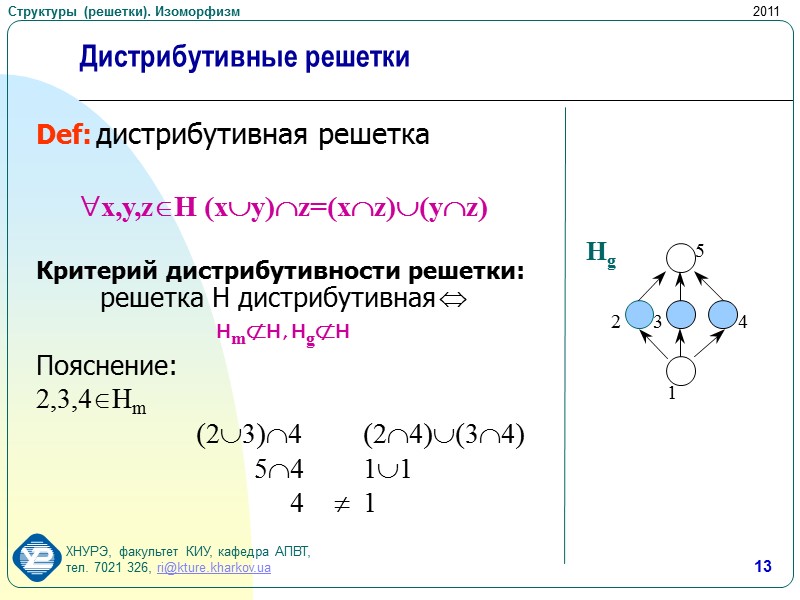
13 Дистрибутивные решетки Def: дистрибутивная решетка x,y,zH (xy)z=(xz)(yz) Критерий дистрибутивности решетки: решетка H дистрибутивная  HmH , HgH Пояснение: 2,3,4Hm (23)4 (24)(34) 54 11 4  1

14 Def: множества M и M* изоморфны, если Def: упорядоченные множества M и M* изоморфны, если между ними существует изоморфизм, сохраняющий порядок Изоморфизм множеств

15 Понятие изоморфизма является одним из важных в математике Любые две алгебры, образованные множествами одинаковой мощности, изоморфны (операции одинаковы, отображение – взаимно-однозначное соответствие множеств-носителей) Суть изоморфизма можно выразить следующим образом: если алгебры А и А* изоморфны, то элементы и операции в алгебре А* можно переименовать так, что А* совпадает с А Изоморфизм алгебр. 1

16 Любое эквивалентное соотношение в алгебре А сохраняется и в любой изоморфной ей алгебре А*, что позволяет автоматически распространять такие соотношения в алгебре А на все изоморфные ей алгебры Указанные обстоятельства дают возможность рассматривать объекты с точностью до изоморфизма, т.е. рассматривать только те свойства объектов, которые сохраняются при изоморфизме В частности, изоморфизм сохраняет ассоциативность, коммутативность, дистрибутивность Изоморфизм алгебр. 2

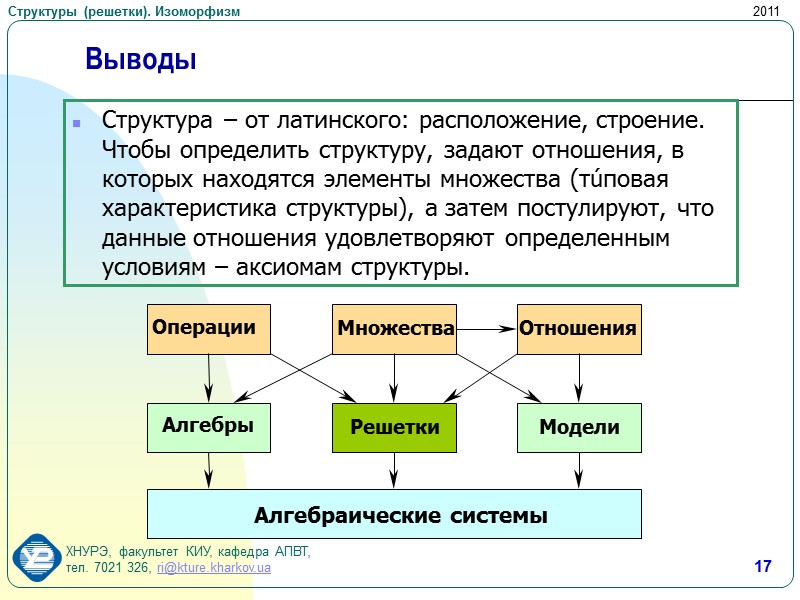
17 Выводы Структура – от латинского: расположение, строение. Чтобы определить структуру, задают отношения, в которых находятся элементы множества (тúповая характеристика структуры), а затем постулируют, что данные отношения удовлетворяют определенным условиям – аксиомам структуры.

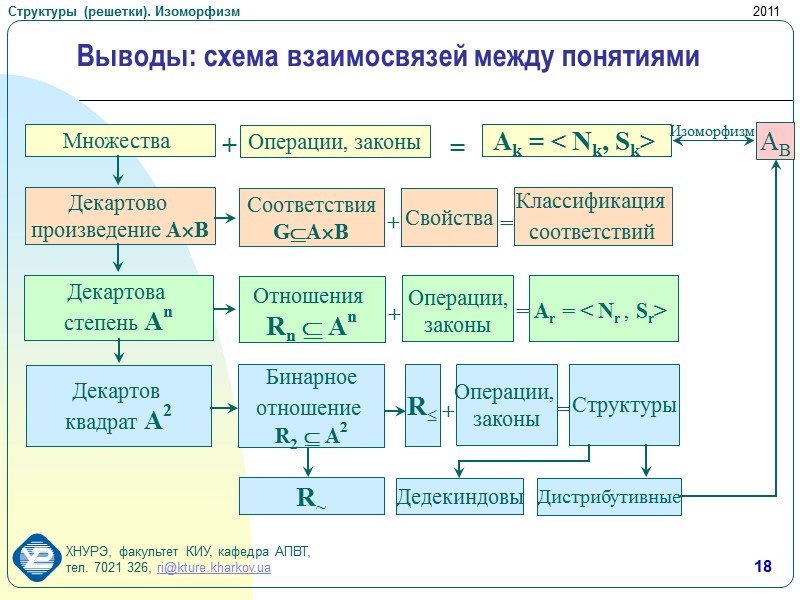
18 Выводы: схема взаимосвязей между понятиями

19 Тест-вопросы 2. Какой из законов не обязательно присутствует в определении решетки: а) коммутативный; б) дистрибутивный; в) элиминации; г) ассоциативный? 3. Какой закон в дополнение к обязательным определяет решетку как булеву алгебру: а) дистрибутивный; б) коммутативный; в) элиминации; г) ассоциативный? 1. Решетка определяется на: а) произвольном множестве; б) линейно упорядоченном множестве; в) частично упорядоченном множестве; г) неупорядоченном множестве?